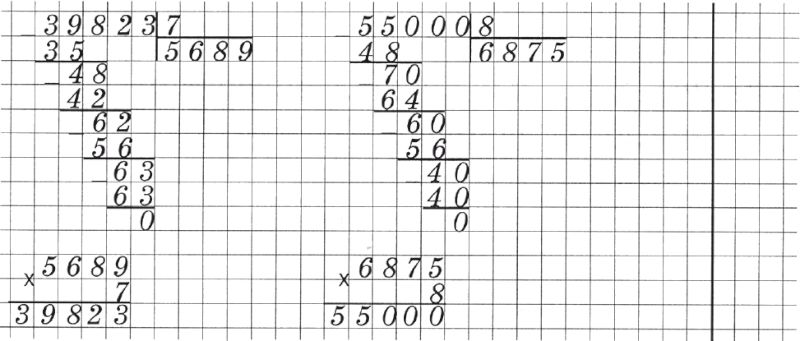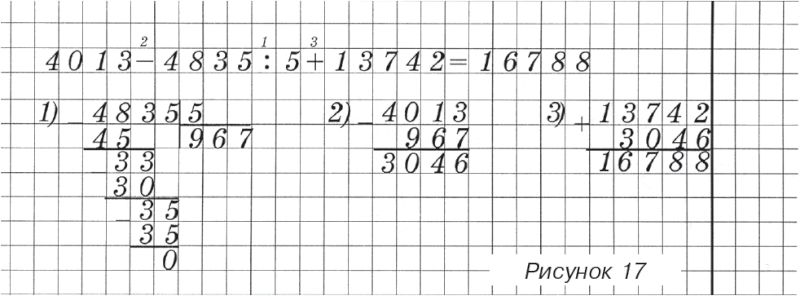Учителя математики и не математики как пишется

Памятка «Оформление задач» (математика)

1 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

Ася вымыла 5 тарелок, а Маша вымыла 4 тарелки. Сколько всего тарелок вымыли дети?

Ася – 5 т.

? Т.

Маша – 4 т.

5 + 4 = 9 (т.)

Ответ: 9 тарелок вымыли дети.

2 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

На стоянке было 2 машины. Вечером приехало ещё 5 машин. Сколько всего машин на стоянке?

Было – 2 м.

Приехало – 5 м.

Стало – ? м.

2 + 5 = 7 (м.)

Ответ: 7 машин всего на стоянке.

3 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

На опушке леса росло 5 клёнов и 4 тополя, а сосен росло столько, сколько клёнов и тополей вместе. Сколько сосен росло на опушке леса?

Клёнов – 5 д.

Тополей – 4 д.

Сосен – ? д.

5 + 4 = 9 (д.)

Ответ: 9 сосен росло на опушке леса.

4 ЗАДАЧА НА

УВЕЛИЧЕНИЕ НА НЕСКОЛЬКО ЕДИНИЦ

У Васи 7 марок, а у Егора на 3 марки больше. Сколько марок у Егора?

Вася – 7 м.

Егор – ? м., на 3 б. >

7 + 3 = 10 (м.)

Ответ: 10 марок у Егора.

5 ЗАДАЧА НА УМЕНЬШЕНИЕ НА НЕСКОЛЬКО ЕДИНИЦ

В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе?

В I г. – 10 уч.

Во II г. – ? уч., на 3 уч. <

10 – 3 = 7 (уч.)

Ответ: 7 учеников во второй группе.

6 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО

У Дины было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Дины?

Розовые – 5 р.

9 р.

Белые – ? р.

9 – 5 = 4 (р.)

Ответ: 4 белые розы были у Дины.

7 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО

Дед Мазай вёз на своей лодке 5 зайцев. Он подобрал ещё несколько зайцев, и их стало 8. Сколько зайцев подобрал дед Мазай?

Было – 5 з.

Подобрал – ? з.

Стало – 8 з.

8 – 5 = 3 (з.)

Ответ: 3 зайца подобрал дед Мазай.

8 ЗАДАЧА НА НАХОЖДЕНИЕ ОСТАТКА

На проводах сидели 9 ворон. 5 ворон улетели. Сколько ворон осталось?

Было – 9 в.

Улетели – 5 в.

Осталось – ? в.

9 – 5 = 4 (в.)

Ответ: 4 вороны осталось.

9 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО

На кустике висело 7 ягод клубники. Когда несколько ягод созрело и упало, осталось 5 ягод. Сколько ягод созрело и упало?

Было – 7 яг.

Упало – ? яг.

Осталось – 5 яг.

7 – 5 = 2 (яг.)

Ответ: 2 ягоды созрело и упало.

10 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО

В зоопарке несколько медведей. Когда трёх медведей перевезли в другой зоопарк, осталось 6 медведей. Сколько медведей было в зоопарке первоначально?

Было – ? м.

Перевезли – 3 м.

Осталось – 6 м.

3 + 6 = 9 (м.)

Ответ: 9 медведей было в зоопарке первоначально.

11 ЗАДАЧА НА РАЗНОСТНОЕ СРАВНЕНИЕ

Один мальчик поймал 8 крабов, а другой 3 краба. На сколько крабов первый мальчик поймал больше второго?

I м. – 8 к. <

на ? >

II м. – 3 к. <

8 – 3 = 5 (к.)

Ответ: на 5 крабов первый мальчик поймал больше, чем второй.

12 ЗАДАЧА НА РАЗНОСТНОЕ СРАВНЕНИЕ

Один арбуз весит 5 кг, а другой 8 кг. На сколько килограммов один арбуз легче другого?

I ар. – 5 кг <

на ? <

II ар. – 8 кг <

8 – 5 = 3 (кг)

Ответ: на 3 килограмма один арбуз легче другого.

13 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

На пришкольном участке 6 берёз, а лип на 4 меньше. Сколько
всего деревьев на пришкольном участке?

Берёз – 6 д.

? д.

Лип – ?д., на 4 д. <

1) 6 – 4 = 2 (д.) – лип.

2) 6 + 2 = 8 (д.)

Ответ: 8 деревьев всего на пришкольном участке.

14 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

В шкафу стоят 2 кастрюли, сковородок на 3 больше, а ваз столько, сколько кастрюль и сковородок вместе. Сколько ваз стоит в шкафу?

Кастрюли – 2 шт.

Сковородки – ? шт., на 3 шт. >

Вазы – ? шт.

Решение

2 + 3 = 5 (шт.) – сковородок.

2 + 5 = 7 (шт.)

Ответ: 7 ваз стоит в шкафу.

15 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

У Тани 3 яблока, груш на 2 больше, чем яблок, а персиков на 4 меньше, чем груш. Сколько всего фруктов у Тани?

Яблоки – 3 шт.

Груши – ? шт., на 2 шт. > ? шт.

Персики – ? шт., на 4 шт. <

Решение

3 + 2 = 5 (шт.) – груш.

5 – 4 = 1 (шт.) – персиков.

3 + 5 = 7 (шт.) – яблок и груш вместе.

7 + 1 = 8 (шт.)

Ответ: 8 фруктов всего у Тани.

16 ЗАДАЧА НА НАХОЖДЕНИЕ СУММЫ

В коробке 17 жёлтых кубиков, зелёных на 6 меньше, чем жёлтых, а красных на 12 больше, чем зелёных и жёлтых кубиков вместе. Сколько всего кубиков в коробке?

Жёлтых – 17 к.

? К.

Зелёных – ? к., на 6 к. < ? К.

Красных — ? к., на 12 к. >

Решение

17 – 6 = 11 (к.) – зелёных.

17 + 11 = 28 (к.) – жёлтых и зелёных вместе.

28 + 12 = 40 (к.) – красных.

28 + 40 = 68 (к.)

Ответ: 68 кубиков всего в коробке.

17 ЗАДАЧА НА НАХОЖДЕНИЕ ОСТАТКА

Нашли 4 белых гриба и 6 подосиновиков. 8 грибов пошло на суп. Сколько грибов осталось?

Было – 4 г. и 6 г.

Израсходовали – 8 г.

Осталось – ? г.

Решение

4 + 6 = 10 (г.) – было.

10 – 8 = 2 (г.)

Ответ: 2 гриба осталось.

18 ЗАДАЧА НА НАХОЖДЕНИЕ ОСТАТКА

У Феди в аквариуме плавали 23 рыбки. Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди?

Было – 23 р.

Подарил – ?, 6 р. и 4 р.

Осталось – ? р.

Решение

6 + 4 = 10 (р.) – подарил.

23 – 10 = 13 (р.)

Ответ: 13 рыбок осталось в аквариуме у Феди.

19 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО

На поле сидело 22 воробья и 13 синичек. Когда прилетело ещё несколько птиц, их стало 49. Сколько птиц прилетело?

Было – 22 п. и 13 п.

Прилетело – ? п.

Стало – 49 п.

Решение

22 + 13 = 35 (п.) – было.

49 – 35 = 14 (п.)

Ответ: 14 птиц прилетело.

20 ЗАДАЧА НА НАХОЖДЕНИЕ ОСТАТКА

У Феди в аквариуме плавали 23 рыбки. Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди?

Было – 23 р.

Подарил – 6 р. и 4 р.

Осталось – ? р.

Решение

6 + 4 = 10 (р.) – подарил.

23 – 10 = 13 (р.)

Ответ: 13 рыбок осталось в аквариуме у Феди.

21 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО

На поле сидело 22 воробья и 13 синичек. Когда прилетело ещё несколько птиц, их стало 49. Сколько птиц прилетело?

Было – 22 п. и 13 п.

Прилетело – ? п.

Стало – 49 п.

Решение

22 + 13 = 35 (п.) – было.

49 – 35 = 14 (п.)

Ответ: 14 птиц прилетело.

22 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО СЛАГАЕМОГО

У причала стояло 6 катеров. Утром причалило 3 катера и несколько катеров причалило вечером, и после этого у причала стало 19 катеров. Сколько катеров причалило вечером?

Было – 6 к.

Причалило – 3 к. и ? к.

Стало – 19 к.

Решение

19 – 6 = 13 (к.) – причалило всего .

13 – 3 = 10 (к.)

Ответ: 10 катеров причалило вечером.

23 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО

Маша увидела 7 белых и 3 пёстрых бабочек. Когда несколько бабочек улетело, их осталось 5. Сколько бабочек улетело?

Было – 7 б. и 3 б.

Улетело –? б.

Осталось – 5 б.

Решение

7 + 3 = 10 (б.) – было.

10 – 5 = 5 (б.)

Ответ: 5 бабочек улетело.

24 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО

На аэродроме было 20 вертолётов. Утром улетело 10 вертолётов. Сколько вертолётов улетело днём, если к вечеру их осталось 6?

Было – 20 в.

Улетели – 10 в. и ? в.

Осталось – 6 в.

Решение

20 – 6 = 14 (в.) – улетели всего.

14 – 10 = 4 (в.)

Ответ: 4 вертолёта улетело днём.

25 ЗАДАЧА НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО

В букете было 9 гвоздик. Когда несколько гвоздик завяли, остались 2 красные и 3 розовые гвоздики. Сколько гвоздик завяло?

Было – 9 г.

Завяли – ? г.

Осталось – 2 г. и 3 г.

Решение

2 + 3 = 5 (г.) – осталось.

9 – 5 = 4 (г.)

Ответ: 4 гвоздики завяло.

26 ЗАДАЧА НА НАХОЖДЕНИЕ ТРЕТЬЕГО СЛАГАЕМОГО

В трёх классах на окнах стоят 35 горшков с цветками. В первом классе 11 горшков, во втором 13. Сколько горшков с цветками стоит в третьем классе?

I к. – 11 г.

II к. – 13 г. 35 г.

III к. – ? г.

Решение

1)11 + 13 = 24(г.) – в I и II классах.

2)35 – 24 = 11(г.)

Ответ: 11 горшков с цветками стоят в третьем классе.

infourok.ru

matematika

Образцы
оформления заданий на уроках математики

В
ходе работы на уроках математики
возникают частные вопросы оформления
отдельных заданий: решения задач,
нахождения значения числовых выражений,
уравнений, неравенств, выполнения
гео­метрических заданий.

Рассмотрим
примерные рекомендации по оформлению
отдельных заданий младшими школьниками
в тетрадях по математике.

Во-первых,
необходимо на­учить младших школьников
легко
определять количество строк, которые
следует пропускать.

Между
работами — 4 клетки, вну­три работы
между заданиями — 2 клетки, внутри
заданий между дей­ствиями — 1 клетку
(образец 1).

Требования
к написанию цифр как
в однозначных числах, так и в многозначных
предъявля­ются единые. Каждая цифра
пи­шется с наклоном в отдельной
клетке, прислоняясь к её правой стороне.
Особенно это требование актуально при
выполнении дей­ствий с многозначными
числами. Образцы написания цифр
пред­ставлены в учебном наглядном
по­собии «Демонстрационный набор
письменных цифр и математичес­ких
знаков».

Во
II классе учащимся удобнее все буквы в
тетрадях по математи­ке писать высотой
в целую клетку (аналогично письму на
уроках язы­ка). В III и IV классах высота
букв при повышении скорости письма
может уменьшаться до 2/3 высоты клетки.

После
даты, слов Домашняя
работа, Классная работа. Зада­ча точка
не ставится. Слова При­меры,
Уравнения, Неравенств, Математический
диктант, Кон­трольный устный счёт в
началь­ных классах не пишутся.

Как
ученику II класса (именно в этом возрасте
они начинают за­писывать дату
выполнения рабо­ты) научиться
определять место
начала записи Даты? Например,
можно договориться отсчитывать от
начала страницы (или от по­лей) 10
полных клеток, а в 11-й начинать запись
даты, тогда будет достигнуто единство
оформления письменных записей и ученику
легко будет расположить дату по­середине
страницы.

Оформление
математических диктантов может
быть выполне­но разными способами.
Учащиеся I класса пишут под диктовку
чис­ла, учатся писать математические
диктанты, записывая результаты в строку
через запятую. Начиная со II класса
результаты диктанта можно оформлять
в строку или в столбики. Учащиеся должны
быть научены фиксировать ответы
по-разному. Перед математическим
диктантом учитель оговаривает с
учащимися способ записи ответов. При
записи результатов математи­ческого
диктанта в строку учащи­еся пишут
каждый последующий результат через
запятую.
В случае отсутствия ответа

на
месте его ученик
ставит прочерк. В против­ном случае
проверка результатов выполненного
диктанта вызовет затруднения, как у
учителя, так и учащихся (при самопроверке
и при взаимопроверке). (Образец 2.)

Запись
результатов матема­тического диктанта
может быть выполнена в столбики. Для
этого перед началом диктанта учитель
сообщает классу количество за­даний
предстоящего диктанта (10 или 12). Учащиеся
до диктанта записывают половину
порядко­вых номеров ответов (5 или 6)
в первый столбик, а вторую полови­ну
— во второй, отступив вправо от записанных
номеров заданий первого столбика
оговоренное количество клеток, например
10. Порядковые номера заданий за­писываются
с круглой скобкой.

В
ходе выполнения математиче­ского
диктанта учащиеся записы­вают ответ
рядом с порядковым номером. Ответы, в
которых уча­щийся сомневается, могут
быть им пропущены. Заполнение их
воз­можно и при самопроверке. Перед
тем как отдать работу на проверку
учителю или однокласснику, уче­ник
должен рядом с номерами не­выполненных
заданий поставить прочерк. (Образец
3.)

В
IV классе при изучении нуме­рации
многозначных чисел фикса­ция
результатов математического диктанта
может производиться в один столбик.
(Образец 4.)

В
оформление
задачи входит
слово Задача,
запись
решения и ответа.

Слово
Задача
записывается
с большой буквы посередине стро­ки.
Ориентировочно необходимо отступить
от левого края страни­цы 10 клеток.
Если запись слова Задача
располагается
на той же странице, что и дата, то учащимся
удобно провести по воздуху ли­нию от
первой цифры даты вниз, так как первая
буква слова будет расположена под
первой цифрой даты. (См. образец 1.)

В
I классе решение задачи запи­сывается
в виде числового выраже­ния. Значение
числового выраже­ния (ответ задачи)
подчёркивается. Полный ответ задачи
проговарива­ется устно. (Образец 5.)

Со
II класса пишутся слова За­дача
и
Ответ.
Второклассники
учатся оформлять запись реше­ния
составной задачи. При запи­си решения
задачи по действиям каждое действие
пишется с новой строки. В начале строки
ставит­ся порядковый номер действия
с круглой скобкой, отступается одна
клетка и записывается действие. (Образец
6.)

Запись
решения задачи мо­жет быть оформлена
выражением. В этом случае порядковый
номер в начале строки не ставится.
(Об­разец 7.)

В
III и IV классах решение мо­жет быть
оформлено по действи­ям без пояснений,
с полными или краткими пояснениями, с
во­просами, с планом, а также вы­ражением.
Если решение задачи записывается
выражением, то нет необходимости делать
пояснения после действия. Результат
поясня­ется только в ответе.

Решение
задачи по действи­ям с краткими
пояснениями

оформляется
следующим образом. Пояснения к каждому
из действий формулируются кратко
(словосоче­танием). Сразу после
наименова­ния ставится тире, и с
маленькой буквы записывается пояснение,
в котором заключается основной смысл
ответа на поставленный во­прос.
(Образец 8.)

Решение
задачи по действи­ям с полными
пояснениями оформляется
следующим образом. (Образец 9.)

Решение
задачи с вопроса­ми предполагает
постановку» во­просов к каждому
из действий. Вопрос записывается с
большой буквы с начала строки. После
него ставится вопросительный знак, а
затем с новой строки записыва­ется
действие. Порядковый номер действия в
этом случае ставится один раз перед
вопросом. (Обра­зец 10.)

Решение
этой же задачи можно оформить с планом.
(Образец 11.)

При
необходимости выполнить письменные
вычисления реше­ние
задачи
записывается сразу в
столбик. (Образец
12.)

Если
решение задачи записы­вается
выражением, при этом не­обходимо
произвести письменные вычисления, они
располагаются под выражением. (Образец
13.)

Наименование
пишется
по­сле каждого действия задачи или
после выражения в скобках с ма­ленькой
буквы. В записи наиме­нования
допускаются сокращения (обязательно
должно заканчивать­ся на согласный).
После сокра­щения ставится точка, в
случаях, если это сокращение не является
общепринятым. Точка не ставится в
наименованиях, обозначающих единицы
измерения длины: мм,
см, дм,
м, км, единицы
измере­ния веса: г,
кг,
т, ц, единицы
из­мерения времени: суг,
ч,
мин, с.

Слово
Ответ
записывается
с начала строки, после него ставит­ся
двоеточие. После двоеточия на первом
месте желательно записать число
(результат решения задачи), а после него
с_ маленькой буквы пояснение к нему.
Ответ задачи может записываться как
целыми словами, так и с использованием
общепринятых сокращений (кило­метров
— км, метров — м, кило­метров в час —
км/ч и т. п.). От­вет записывается к
каждой задаче.

В
случае если задача решается несколькими
способами, делает­ся пометка «1
способ,
2
способ»
и ответ записывается один раз. Ес­ли
решение задачи записано по действиям,
а затем выражением, то ответ тоже
записывается один
раз.
Если решение задачи выпол­нялось с
полным пояснением, с записью вопросов
по действиям, ответ может быть записан
кратко. При этом записывается числовое
значение и наименование либо число и
словосочетание, отражающие
ответ задачи. (См. образцы 9, 10, 11.) Если
решение задачи за­писано выражением,
по действиям с краткими пояснениями
или без них, то ответ задачи должен быть
полным (в виде числа и предложе­ния).
(См. образцы 6, 7, 8, 12, 13.)

К
задаче может быть выполне­на краткая
запись. Она записыва­ется после слова
Задача.
Между
строками пропускается одна клет­ка.
Буквы и цифры пишутся в соот­ветствии
с рассмотренными выше требованиями.

Запись
нахождения значения математического
выражения также
оформляется единообразно. Если
математическое выражение состоит из
одного действия, кото­рое решается
устно, ученик запи­сывает его в строку
и рядом — его ответ. При записи нескольких
таких выражений между столбиками
ре­комендуется пропускать в сторону
3 клетки, а вниз между столбика­ми —
2. (Образец 14.)

Если
математическое выраже­ние состоит
из одного действия, и для его решения
требуются письменные вычисления, то
оно сразу записывается в столбик и
вычисляется. В
строке
можно раз­местить несколько
математических выражений с письменными
вычис­лениями при условии, что вправо
между ними необходимо пропу­скать
не менее 3 клеток. (Обра­зец 15.)

При
письменном умножении на трёхзначное
число следует реко­мендовать учащимся
размещать на одной строке только 2
приме­ра, так как при записи происходит
значительный сдвиг влево. При
не­обходимости на строке размеша­ется
математическое выражение, а рядом
проверка вычислений. (Об­разец 16.)

Учащийся
вправе сам принять решение о рациональном
разме­щении на странице выполненных
заданий. К примеру, если необ­ходимо
выполнить несколько при­меров на
деление многозначных чисел и сделать
к ним проверку, на одной строке можно
разме­стить примеры на деление, а под
ними проверку. В таких случа­ях
рекомендуется отступать вниз 2 клетки.
(Образец 17.)

Если
математическое выраже­ние состоит
из нескольких дей­ствий, решение
которых пред­полагает устные
вычисления, то учащийся сначала
определяет порядок
действий (его можно над­писать над
выражением), затем производит устные
вычисления и записывает ответ. Выполнять
за­пись устных действий не нужно.
(Образец 18.)

Если
математическое выраже­ние состоит
из нескольких дей­ствий, решение
которых предпо­лагает письменные
вычисления, то сначала оно записывается
в строку. Определяется порядок выполнения
действий. Затем каждое действие
записывается под выражением и выполняется.
Полученный конечный результат
записывается в первоначальную запись
после знака «равно». (Об­разец 19.)

Решение
простейшего урав­нения записывается
в столбик: само уравнение, способ
нахож­дения неизвестного, результат
вычисления (значение неизвест­ного),
проверка решения уравне­ния. Можно
расположить реше­ние двух уравнений
в 2 столбика. При этом между уравнениями
в сторону необходимо отступить 3 клетки.
Слова Решение

и
Про­верка,
которые
используются в

образце
оформления уравнения на страницах
учебника, в
тетрадях
учащимися не записываются. (Об­разец
20.)

Решение
уравнений в два дей­ствия также
записывается в стол­бик. Расположение
двух таких уравнений также допустимо
на одной строке при условии, что их
решение не требует письменных вычислений.
(Образец 21.)

Если
при решении уравнения необходимо
выполнять письмен­ные действия с
многозначными числами, их следует
располагать справа от записи решения
уравне­ния. (Образец 22.)

Сравнение
чисел, выраже­ний, величин. При
сравнении двух чисел они записываются
на строке с интервалом в одну клетку.
В ней учащийся ставит знак. (Об­разец
23.)

При
сравнении многозначных чисел учащийся
производит срав­нение поразрядно.
Достаточно об­ратить внимание на
различающие­ся цифры в разрядах,
начиная с высшего, подчеркнуть их. Во
вто­рой строке можно записать только
те цифры, которыми различаются числа.
Это будет основанием для сравнения
чисел. (Образец 24.)

Если
число необходимо срав­нить с выражением,
то в записи между ними также оставляется
клетка. Знак может быть вставлен только
после нахождения значения выражения
и сопоставления его с числом. (Образец
25.)

Если
необходимо сравнить
два выражения, то
в записи меж­ду ними также оставляется
клетка. Знак может быть вставлен только
после нахождения значений обоих
выражений. Найденные значения выражений
целесообразно запи­сать на следующей
строке и после их сопоставления поставить
знак сравнения между ними, а затем и
на верхней строке в исходном вы­ражении.
(Образец 26.)

При
сравнении
величин об­ращается
внимание на единицы их измерения. Если
величины вы­ражены в одинаковых
единицах измерения, то сравнение
произ­водится так же, как и сравнение
чисел. Знак ставится между ве­личинами
после установления их равенства или
неравенства. (Об­разец 27.)

Если
сравниваются величины, выраженные в
разных единицах измерения, необходимо
оценить возможность их сравнения без
приведения их к единым едини­цам
измерения; если это возмож­но, поставить
требующийся знак. (Образец 28.)

При
сравнении величин, вы­раженных в
разных единицах из­мерения, чаще
всего обязатель­ным условием является
приведе­ние их к одинаковым единицам
(меньшим или большим). Запись лучше
зафиксировать на следую­щей строке.
После сопоставления преобразованных
величин мож­но поставить знак равенства
или
неравенства
и
затем перенести его в исходное выражение.
(Об­разец 29.)

Задания
геометрического характера могут
включать толь­ко вычерчивание
геометрических фигур, только нахождение
параме­тров геометрических фигур,
либо задание на нахождение параме­тров
и вычерчивание фигур.

Если
задание предполагает только вычерчивание
фигуры (фи­гур), от предыдущего задания
от­ступают две клетки и чертят
за­данную геометрическую фигуру.

Если
задание предполагает только нахождение
параметров геометрической фигуры, то
ученик должен оформить выполнение
за­дания как решение задачи: слово
Задача,
решение
(нахождение па­раметров геометрической
фигуры), ответ. Если в задаче не требуется
вычерчивание фигуры, этого и не нужно
делать. (Образец 30.)

Если
задание предполагает нахождение
параметров и вычер­чивание фигуры,
то оформляется это тоже как задача.
Ученик дол­жен привыкнуть к тому, что
любые вычисления (даже устные) при
нахождении параметров должны быть
зафиксированы письменно. Сначала
проводятся вычисления, затем вычерчивается
фигура с полученными данными. (Обра­зец
31.)

В
задании может быть задана длина первого
отрезка. Второй и третий отрезки
необходимо найти, а затем начертить. В
таком случае ребёнку удобно начертить
данный отрезок, вычислить размер
второ­го отрезка (с записью действия),
начертить полученный отрезок, за­тем
найти длину третьего отрезка (с записью
действия) и тогда его начертить. (Образец
32.)

Это
же задание учащийся может оформить
иначе. (Обра­зец 33.)

Если
к заданию было записа­но слово Задача,
значит,
к нему предполагается и Ответ.

Если
необходимо произвести сравнение
отрезков, значит, за­
писывается слово
Задача,
после
вычерчивания отрезков записыва­ется
математическое действие, с помощью
которого производилось сравнение
(вычитание, деление). Завершается
выполнение задания записью ответа.

Отметим
некоторые особенно­сти
вычерчивания отрезков.

• Чертим
  отрезки, отступая от левого края
  страницы 1 полную клетку.

• Все
  отрезки необходимо чертить друг под
  другом, при этом их начальные точки
  должны на­ходиться на одном расстоянии
  от левого края страницы.

• Пропуски
  между отрезками вниз составляют 1
  клетку.

• Края
  отрезков отмечаются небольшими
  штрихами.

Нахождение
значения выра­жения с переменной
записывает­ся следующим образом.
(Обра­зец 34.)

Требования
к оформлению контрольных работ.
Оформле­ние
их производится так же, как и классных
работ. Исправления делаются в случае
необходимости аккуратно. Краткая запись
к зада­че, вопросы, пояснения, которые
помогают при обучении решению задач,
в контрольной работе не требуются, так
как их использо­вание часто влечёт
множество ор­фографических ошибок,
не отра­жающих реальные математические
знания детей. Формулировки зада­ний
контрольной работы учащими­ся не
переписываются в тетрадь. Ставится
лишь порядковый номер выполняемого
задания.

Порядок
выполнения заданий контрольной работы
учащийся мо­жет выбрать сам. Записывая
ре­шения заданий, он должен ставить
тот
порядковый
номер задания, под которым оно стоит в
контроль­ной работе. (Образец 36.)

Хочется
отметить, что
далеко не все частные случаи оформ­ления
записей по
математике удалось осветить в статье.
Кро­ме того, прописанные
в данной статье рекомендации являются
примерными. Если
учителем, ме­тодическим объединением
учите­лей наработаны более рациональ­ные
приёмы обучения учащихся оформлению
записей в тетрадях по математике без
нарушения общепринятых норм, они имеют
право внедрять их в свою деятель­ность.
Важным
остаётся требо­вание единообразия
оформле­ния записей всеми учащимися.

Работа
по формированию у младших школьников
культуры оформления записей в тетрадях
по математике кропотливая, тре­бует
терпения. Однако
необходи­мо помнить, что эти условности,
используемые школьниками, не отражают
математической под­готовки учащихся,
поэтому не следует строго наказывать
уча­щихся за то, что кто-то из них
пропустил не 10, а 11 клеток при записи
даты или допустил и прочие отклонения.
Важно,
что­бы записи были рациональными,
единообразными, экономичными, лаконичными
и при этом эстетично оформленными.

Литература:

1. Н.
   Л. Ковалевская,
   учитель
   высшей категории, методист высшей
   категории,

г.
Минск//Пачатковае
навучанне: сям’я,
дзіцячы сад, школа, 2012 г., № 10, стр. 5-12

16

studfiles.net

Как оформить задачи по математике

27 декабря 2018

Автор КакПросто!

Правильное оформление задачи является одним из важных условий получения положительной оценки за работу. Более того, некорректно поданное решение, особенно если дело касается вузов, может и вовсе послужить недопуском к защите контрольной работы или домашнего задания.

Статьи по теме:

Инструкция

Ознакомьтесь с методическими рекомендациями вашего учебного заведения относительно правильного оформления различных работ по математике. Если таковых нет, используйте стандартные правила оформления задач. Используйте всегда только ручки и карандаши черных, синих и фиолетовых цветов. Изредка возможно дополнительное оформление отдельных моментов зеленым цветом. Учтите, что красная гамма исключительно для преподавателя. При оформлении задачи обязательно должны быть оставлены поля с одной из сторон листа, шириной не менее 1,5-2 см. Написание работы начините с указания текущей даты, типа задания – это может быть «домашняя работа», «подготовка к контрольной работе», «аттестационная работа» и так далее. Далее изложите условие задачи — напишите слово «Условие», поставьте после него двоеточие и с маленькой буквы перепишите данные. Если это позволено преподавателем, можно просто указать вариант и написать порядковый номер задачи.

Если заданий несколько, решайте их в любой последовательности – это никак не повлияет на будущую оценку. Главное, правильно указать номер и не перепутать условия.

Приступая к решению, оформите его словом «Решение» и после двоеточия излагайте свои знания. Первыми, как правило, указываются формулы, теоремы и правила, на которые вы опираетесь при решении. Сначала указывается формула, после этого идет непосредственно ее применение. Теоремы не нужно дословно цитировать, достаточно просто сослаться на них, указав название.

При решении показывайте ход своих мыслей, дополняя текст словами, типа «поскольку», «согласно», «так как», «допустим, что», «таким образом», «сделаем вывод» и так далее.

Обязательно оформляйте задачи по математике соответствующими графиками, чертежами, таблицами и другими аналогичными элементами. При этом все они должны рисоваться твердым тонким карандашом. Рисунки должны быть четкими и аккуратными. Неправильно сделанный рисунок считается большой ошибкой, поскольку заранее предопределяет неверное решение задачи. В графиках должны быть грамотно указаны единицы измерения, обозначения осей координат.

После решения каждой задачи, выделяйте «Ответ» и подытоживайте сделанные выводы и полученный результат. В конце всей работы оставьте место для пометок и рецензии преподавателя. С этой же целью оставляйте небольшое количество места после каждой решенной задачи.

Если работа по математике будет представляться учебному руководителю на отдельном листе, поместите решение задач внутрь двойного листка, оставив титульную страницу для указания типа работы, вашего имени и фамилии, учебного заведения, класса (для школы) или факультета, кафедры и группы (для вузов). Не всегда приемлема сдача работы на одинарном листе либо же на отдельной его части.

www.kakprosto.ru

Сообщение на тему «Различные способы оформления условия решения и оформления решения математических задач»

1. Муниципальное автономное общеобразовательное учреждение

   1. городского округа Балашиха Московской области

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 26»

143909 Московская область, г. Балашиха, ул. Летная, д.10

e-mail: bal—school[email protected]yandex.ru Tелефон: 8(498)-504-73-02

ИНН 5001105630 КПП 500101001 ОГРН 1155001004432 Лицензия № 74778 от 23.11.2015г

.Сообхщение на тему:

«Различные способы оформления условия решения и оформления решения математических задач«

Подготовила

Учитель начальных классов Орлова Наталья Викторовна

Балашиха 2016г .

Способы решения математических задач на конкретном примере

Задача. Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные – щуки. Сколько щук поймал рыбак?

Способы решения задачи:

1. Практический (предметный) способ.

Учащиеся могут решить эту задачу, опираясь только на свой жизненный опыт и владея счетом от 1 до 10.

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим пойманных рыб: л – лещи, о – окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их три).

2. Арифметический способ.

Этот метод основывается на арифметических действиях.

1. 3+4=7 (р.) – пойманные рыбы;

2. 10–7=3 (р.) – щуки.

Для ответа на вопрос задачи выполнили 2 действия.

3. Алгебраический способ.

Этот способ основывается на введении неизвестной переменной и на нахождении ее.

Пусть х – пойманные щуки. Тогда количество всех рыб можно записать выражением: 3+4+х – все рыбы.

По условию задачи известно, что рыбак поймал всего 10 рыб. Значит: 3+4+х=10. Решив это уравнение ответим на вопрос задачи: х=3.

4. Графический способ.

Этот способ решения близок к практическому, но носит более абстрактный характер и требует специального разъяснения. Каждый объект задачи обозначается отрезком.

Рисунок

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

5. Комбинированный способ.

В нем могут быть использованы одновременно графический и арифметический способы.

1) 3+4=7 (р.) – пойманные рыбы;

2) 10–7=3 (р.) – щуки.

Способы оформления решения задач на примере конкретной задачи

Задача. У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую, остальные – на третью. Сколько книг на третьей полке.

Различные формы записи решения задачи:

а) Решение по действиям:

1) 28+12=40 (к.)

2) 90–40=50 (к.)

Ответ: 50 книг на третьей полке.

б) По действиям с пояснением:

1) 28+12=40 (к.) – на 1 и 2 полках вместе,

2) 90–40=50 (к.) – на 3 полке.

Ответ: 50 книг.

в) С вопросами:

1) Сколько книг на 1 и 2 полках месте?

28+12=40 (к.)

2) Сколько книг на 3 полке?

90–40=50 (к.)

Ответ: 50 книг на третьей полке.

г) Выражением:

90 – (28+12)

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 – (28+12)=50 (к.)

Способы оформления краткой записи на примере конкретной задачи

Задача. У одной закройщицы было 15 м ткани, у другой – 12 м. Из всей ткани они скроили платья, расходуя на каждое по 3 м. Сколько всего платьев они скроили?

1-й способ: 1) 15+12=27 (м),

2) 27:3=9 (п.).

Ответ: 9 платьев скроили.

2-й способ: 15:3+12:3=9 (п.)

Ответ: 9 платьев скроили.

3-й способ: 1) 15:3=5 (п.),

2) 12:3=4 (п.).

3) 5+4=9 (п.).

Ответ: 9 платьев скроили.

infourok.ru

Памятка по математике для 1 класса «Как оформлять задачи»

Как правильно оформлять краткую запись задачи

1. Задачи на увеличение и уменьшение числа на несколько единиц:

У Маши было 5 конфет, а у Вовы на 2 конфетки больше. Сколько конфет было у Вовы?

М. – 5 к.

В. — ?, на 2 к. >

5 + 2 = 7 (к.)

Ответ: 7 конфет.

У Маши было 5 конфет, а у Вовы на 2 конфетки меньше. Сколько конфет было у Вовы?

М.- 5 к.

В.- ?, на 2 к. <

5 – 2 = 3 (к.)

Ответ: 3 конфеты.

2. Задачи в два действия:

У Маши было 5 конфет, а у Вовы на 2 конфетки больше. Сколько всего конфет было у Вовы и Маши вместе?

М. – 5 к. ? к.

В. — ?, на 2 к. >

1) 5 + 2 = 7 (к.) – у Вовы.

2) 5 + 7 = 12 (к.) – всего. Или (5+2) + 7 =12(к.)

Ответ: 12 конфет.

У Маши было 5 конфет, а у Вовы на 2 конфетки меньше. Сколько всего конфет было у Маши и Вовы ?

М. – 5 к. ? к.

В. — ?, на 2 к. <

1) 5 — 2 = 3 (к.) – у Вовы.

2) 3 + 7 = 10 (к.) – всего. Или (5 – 2) + 7= 10(к.)

Ответ: 10 конфет.

3. Задачи на нахождение остатка:

В тарелке было 5 слив. Аня съела 3 сливы. Сколько слив осталось?

Б. – 5 с.

С.- 3 с.

О. — ?

5 – 3 = 2 (с.)

Ответ: 2 сливы.

4. Составная задача.

На стоянке было 5 машин. Потом уехали 3 машины, а приехали 6. Сколько машин стало на стоянке?

Б. – 5 м.

У. – 3 м.

П. – 6 м.

Стало? м.

5 – 3 + 6 = 8 (м.)

Ответ: стало 6 машин.

4. Задачи на разностное сравнение:

(Для этих задач работает правило: из большего числа отнимаем меньшее, решение одинаковое, но ответы звучат по-разному)

Слив было 5, а яблок – 7. На сколько больше было яблок, чем слив?

С. – 5 На ? я. >

Я.- 7

7 – 5 = 2 (я.)

Ответ: на 2 яблока

Слив было 5, а яблок – 7. На сколько меньше слив, чем яблок?

С. – 5 На ? с. <

Я. – 7

7 – 5 = 2 (с.)

Ответ: на 2 сливы <

infourok.ru

Учебно-методический материал по математике (1 класс) по теме: Оформление задач на уроках математики в начальной школе

Задача №1.

Аня вымыла 5 тарелок, а Дима вымыл 3 тарелки. Сколько всего тарелок вымыли дети?

Задача.

Аня – 5 т.                ? т.

Дима – 3 т.

5+3=8 (т.)

Ответ: 8 тарелок вымыли дети.

Задача №2.

На стоянке было 2 грузовика. Вечером приехало еще 5 грузовиков. Сколько всего грузовиков на стоянке.

Задача.

Было – 2 гр.

Приехало – 5 гр.

Стало — ? гр.

2+5=7 (гр.)

Ответ: 7 грузовиков всего на стоянке.

Задача №3.

На опушке леса росло 5 кленов и 4 тополя, а сосен росло столько, сколько кленов и тополей вместе. Сколько сосен росло на опушке леса.

Задача.

Кленов – 5 д.

Тополей – 4 д.

Сосен — ? д., К.+Т.

5+4=9 (д.)

Ответ: 9 сосен росло на опушке леса.

Задача№4.

У Васи 7 марок, а у Егора на 3 марки больше. Сколько марок у Егора?

Задача.

Вася – 7 м.

Егор — ?, на 3 м. б.

7+3=10 (м.)

Ответ: 10 марок у Егора.

Задача №5.

В первом классе 10 учеников, а во втором классе на 3 ученика меньше. Сколько учеников во втором классе?

Задача.

В I кл. – 10 уч.

Во II кл. — ?, на 3 уч. м.

10-3=7 (уч.)

Ответ: 7 учеников во втором классе.

Задача №6.

У Ани было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Ани?

Задача.

Розовые – 5 р.            9 р.

Белые — ? р.

9-5=4 (р.)

Ответ: 4 белые розы у Ани.

Задача №7.

Дед Мазай вез на своей лодке 5 зайцев. Он подобрал еще несколько зайцев, и их стало 8. Сколько зайцев подобрал дед Мазай?

Задача.

Было – 5 з.

Подобрал — ? з.

Стало – 8 з.

8-5=3 (з.)

Ответ: 3 зайца подобрал дед Мазай.

Задача №8.

На проводах сидели 9 ворон. 5 ворон улетели. Сколько ворон осталось?

Задача.

Было – 9 в.

Улетели – 5 в.

Осталось — ? в.

9-5=4 (в.)

Ответ: 4 вороны осталось.

Задача №9.

На кустике висело 7 ягод клубники. Когда несколько ягод созрело и упало, осталось 5 ягод. Сколько ягод созрело и упало?

Задача.

Было – 7 яг.

Упало — ? яг.

Осталось – 5 яг.

7-5=2 (яг.)

Ответ: 2 ягоды созрело и упало.

Задача №10.

В зоопарке несколько медведей. Когда трех медведей перевезли в другой зоопарк, осталось 6 медведей. Сколько медведей было в зоопарке сначала?

Задача.

Было — ? м.

Перевезли – 3 м.

Осталось – 6 м.

3+6=9 (м.)

Ответ: 9 медведей было в зоопарке.

Задача №11.

Один мальчик поймал 8 крабов, а другой 3 краба. На сколько крабов первый мальчик поймал больше второго?

Задача.

1 м. – 8 к.           на ? больше

2 м. – 3 к.

8 – 3=5 (к.)

Ответ: на 5 крабов первый мальчик поймал больше, чем второй.

Задача №12.

Один арбуз весит 5 кг., а другой 8 кг. На сколько кг один арбуз легче другого?

Задача.

1 ар. – 5 кг          на ? меньше

2 ар. – 8 кг

8-5=3 (кг)

Ответ: на 3 кг один арбуз легче другого.

nsportal.ru

Памятка по математике для 1 класса (оформление задач).

Задачи в 1 действие

1 мешок – 4 кг

2 мешок — ? на 3 кг б.

4 + 3 = 7 (кг)

Ответ: 7 кг весит 2 мешок.

Маша – 8 игр.

Катя — ? на 2 игр. м.

8 – 2 = 6 (игр.)

Ответ: 6 игрушек у Кати.

Синих – 4 фл. ? фл.

Красных – 6 фл.

4 + 6 = 10 (фл.)

Ответ: 10 флажков всего.

С капустой – 3 п. 9 п.

С картошкой — ? п.

9 – 3 = 6 (п.)

Ответ: 6 пирожков с картошкой.

Сестра – 10 л.

Брат – 7 л.

10 – 7 = 3 (г.)

Ответ: на 3 года сестра старше.

Слив – 5 шт.

Груш – 4 шт.

Яблок — ? шт.

5 + 4 = 9 (шт.)

Ответ: 9 штук яблок.

Было – 15 ящ.

Продали – 5 ящ.

Осталось — ? ящ.

15-5 = 10 (ящ.)

Ответ: 10 ящиков осталось.

Было – 15 ящ.

Продали – ? ящ.

Осталось — 10 ящ.

15 — 10 = 5 (ящ.)

Ответ: 5 ящиков продали.

Было – ? ящ.

Продали – 5 ящ.

Осталось — 10 ящ.

10 + 5 = 15 (ящ.)

Ответ: 15 ящиков было.

Стояло – 2 м.

Приехали – 8 м.

Стало — ? м.

2 + 8 = 10 (м.)

Ответ: 10 машин стало.

Стояло – 2 м.

Приехали – ? м.

Стало — 10 м.

10 – 2 = 8 (м.)

Ответ: 8 машин приехали.

Стояло – ? м.

Приехали – 8 м.

Стало — 10 м.

10 – 8 = 2 (м.)

Ответ: 2 машины стояли.

Задачи в 2 действия

1 ваза – 4 ябл. ? ябл.

2 ваза — ? на 2 ябл. б.

1) 4 + 2 = 6 (ябл.) – во 2 вазе.

2) 6 + 4 = 10 (ябл.) – всего.

(4+2)+4 = 10 (ябл.)

Ответ: 10 яблок всего.

Петя – 7 рыб ? рыб

Вася — ? на 4 рыб м.

1) 7 — 4 = 3 (р.) – у Васи.

2) 3 + 7 = 10 (р.) – вместе.

(7-4)+7 = 10 (р.)

Ответ: 10 рыбок поймали ребята.

Морковь – 6 кг

Свекла – 3 кг

1) 6 + 3 = 9 (кг) – всего.

2) 6 – 3 = 3 (кг) – меньше свёклы, чем моркови.

Ответ: 9 кг, на 3 кг меньше.

Слив – 5 шт.

Груш – ? на 1 шт. м.

Яблок — ? шт.

1) 5 – 1 = 4 (шт.) – груш.

2) 5 + 4 = 9 (шт.) – яблок.

5 + (5-1) = 9 (шт.)

Ответ: 9 яблок в сумке.

1 полка – 5 книг

2 полка — ? книг 10 кн.

3 полка – 2 книги

1 способ:

1) 5 + 2 = 7 (кн.) – на 1 и 3 полках.

2) 10 – 7 = 3 (кн.) – на 2 полке.

10 – (5+2) = 3 (кн.)

2 способ 10 – 5 – 2 = 3 (кн.)

Ответ: 3 книги на второй полке.

Было — 6 и 5 м.

Уехали – 4 м.

Осталось — ? м.

1) 6 + 5 = 11 (м.) – было.

2) 11 – 4 = 7 (м.) – осталось.

2 способ (6 – 4) + 5 = 7 (м.)

3 способ (5 — 4) + 6 = 7 (м.)

Ответ: 7 машин осталось.

Было — ? м.

Уехали – 3 гр. и 7 лег. м.

Осталось — 1 м.

1) 3 + 7 = 10 (м.) – уехали.

2) 1 + 10 = 11 (м.) – было.

2 способ (3 + 1) + 7 = 11 (м.)

3 способ (7 + 1) + 3 = 11 (м.)

Ответ: 11 машин было.

ВСЕГО

ВМЕСТЕ

НА СКОЛЬКО БОЛЬШЕ

НА СКОЛЬКО МЕНЬШЕ

СТОЛЬКО,

СКОЛЬКО

… И … ВМЕСТЕ

— … И …

infourok.ru

Успех в получении знаний по математике начинается с правильного и аккуратного оформления тетради, так как это воспитывает у учащихся внутреннюю культуру; уважение к своему труду; уважение к педагогу и другим людям, которые смотрят тетради; последовательность и системность в работе; внимательность и мн. др. С целью формирования у учащихся навыков аккуратного ведения записей педагогу следует систематически уделять внимание каллиграфии и формированию умения оформлять выполненную в течение учебного занятия работу в тетрадях.

В процессе работы педагога на уроках математики возникают частные вопросы оформления отдельных заданий.

Рассмотрим примерные рекомендации по оформлению отдельных заданий на I ступени общего среднего образования в учебных тетрадях по учебному предмету «Математика»: решения задач, нахождения значения числовых выражений, уравнений, неравенств, выполнения геометрических заданий.

Согласно документу «Метадычныя рэкамендацыі па фарміраванні культуры вуснага і пісьмовага маўлення ва ўстановах адукацыі, якія рэалізуюць адукацыйныя праграмы агульнай сярэдняй адукацыі» учебные и контрольные работы по учебному предмету «Математика» учащиеся I класса выполняют в соответствующих тетрадях на печатной основе [1]. Для выполнения учебных и контрольных работ по математике учащимся II–IV классов рекомендуется иметь 3 тетради (2 тетради для учебных работ и 1 тетрадь для контрольных работ). Все записи в тетрадях делаются ручкой с пастой синего или фиолетового цвета (по решению учреждения образования) аккуратно, разборчивым почерком, исправления выполняются без использования корректора. Чертежи, схемы, графики, таблицы, диаграммы, рисунки выполняются аккуратно карандашом (при необходимости цветными карандашами, кроме красного) или ручкой, при необходимости — с применением линейки и циркуля.

Предъявляются единые требования к написа­ нию цифр в однозначных и многозначных числах. Цифры следует писать с наклоном в отдельной клетке, к правой стороне. Необходимо соблюдать соответствие между количеством цифр в числе и количеством клеток для его записи. Образцы написания цифр представлены в учебном наглядном пособии «Демонстрационный набор письменных цифр и математических знаков».

Начинаем писать в тетради со 2-й сверху полной клетки. Часто разлиновка в тетрадях в клетку может начинаться с «неполной» клетки, поэтому следует пропустить сверху страницы одну «полную» клетку и начинать запись со второй.

Во ІІ–ІV классах дата выполнения учебной или контрольной работы записывается посередине строки: день месяца арабской цифрой, название месяца — прописью.

Для того чтобы ученику II класса научиться определять место начала записи даты и легко
расположить дату посередине страницы, можно договориться отсчитывать от начала страницы (или от полей) слева 10 полных клеток, а в 11-й начинать запись даты, тогда будет достигнуто единство оформления письменных записей.

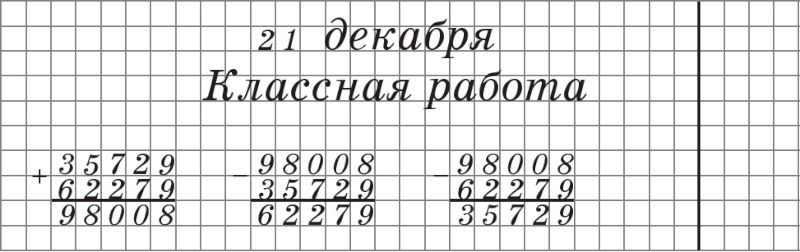
На следующей строчке (посередине) после даты в учебных тетрадях пишется Классная работа или Домашняя работа. Между датой и словами Классная работа или Домашняя работа пропускается одна клетка вниз, между словами Классная работа или Домашняя работа и заданием — 2 клетки вниз. (Рис. 1.)

Следует отметить, что во II классе все буквы в тетрадях по математике учащимся удобнее будет писать аналогично письму на уроках языка — высотой в целую клетку. При повышении скорости письма высота букв может уменьшаться до 2/3 высоты клетки (в III и IV классах).

После даты, слов Домашняя работа, Классная работа, Задача точка не ставится. Желательно запись даты, слов Классная работа, Домашняя работа располагать вместе с содержанием работы, не отрывая от основного текста (не оставлять на другой странице).

Слова «примеры», «уравнения», «неравенства», «проверка навыков устного счёта» во ІІ–ІV классах не пишутся.

Для отделения одной учебной работы от второй и для выставления отметки пропускаются четыре клетки вниз.

Одним из важных видов работы является подготовка к проверке навыков устного счёта, которая проводится дважды в течение учебного года. Проходит эта подготовка в виде заданий для устных вычислений (математических диктантов). Оформление результатов диктанта может быть выполнено разными способами: в строку или в столбики. Педагогу следует обучить учащихся фиксировать ответы по-разному. Перед проверкой учитель оговаривает с учащимися способ записи ответов. При записи результатов математического диктанта в строку учащиеся пишут каждый последующий результат через запятую. В случае отсутствия ответа на его месте нужно поставить прочерк, что предотвратит затруднения как у учителя, так и у учащихся при проверке результатов выполненного диктанта (при самопроверке и при взаимопроверке). (Рис. 2.)

Второй способ фиксации результатов — запись в столбики. Перед началом проверки навыков устного счёта учитель сообщает классу о способе фиксации результатов. Согласно пункту 2.4 документа «Нормы оценки результатов учебной деятельности по учебным предметам на I ступени общего среднего образования» проверка устного счёта включает 10 заданий. Учащиеся до диктанта записывают половину порядковых номеров ответов (5) в первый столбик, а вторую половину — во второй, отступив вправо от записанных номеров заданий первого столбика оговорённое количество клеток, например 10 [2]. Порядковые номера заданий записываются с круглой скобкой. В ходе выполнения диктанта учащиеся записывают ответ рядом с порядковым номером. Рядом с номерами невыполненных заданий следует поставить прочерк. (Рис. 3.)

В IV классе при изучении нумерации многозначных чисел фиксация результатов проверки навыков устного счёта может осуществляться в один столбик. (Рис. 4.)

В тетрадях по учебному предмету «Математика» начиная со ІІ класса при оформлении решения заданий на отдельной строке указывается вид учебной работы — задача. Между названием вида задания, решением и ответом пропускается соответственно одна клетка вниз. Слово решение перед решением задачи не записывается. Таким образом, в оформление задачи входят слово Задача, запись решения и Ответ.

Слово Задача записывается с большой буквы посередине строки. Ориентировочно, как и при записи даты, необходимо отступить от левого края страницы 10 клеток. Если запись задачи располагается на той же странице, что и дата, то учащимся удобно провести воображаемую линию от первой цифры даты вниз, первая буква слова Задача будет расположена под первой цифрой даты. (См. рис. 5.)

Одним из этапов работы над задачей является анализ текста задачи и интерпретации условия задачи [3].

К видам интерпретации условия задачи относятся краткие записи текста задачи, схемы, предметные иллюстрации. Интерпретация условия — необязательный этап в работе над задачей. Необходимость в ней возникает тогда, когда учащиеся затрудняются в решении задачи. Учитель вправе выбирать и разрабатывать свои способы интерпретации условия. К задачам может быть выполнена краткая запись. Она записывается после слова Задача. Между строками пропускается одна клетка. Буквы и цифры пишутся в соответствии с рассмотренными выше требованиями.

Основной способ записи решения составных задач на I ступени общего среднего образования — по действиям. Запись решения выражением даётся в ознакомительном плане [3]. При записи решения составной задачи по действиям каждое действие пишется с новой строки. В начале строки ставится порядковый номер действия с круглой скобкой, отступается одна клетка и записывается действие. (Рис. 5.)

У Пети 7 конфет, у Лены на 2 конфеты меньше. Сколько всего конфет у детей?

При оформлении решения задачи выражением порядковый номер в начале строки не ставится. (Рис. 6.)

В III и IV классах решение может быть оформлено разными способами: по действиям без пояснений, с полными или краткими пояснениями, с вопросами, с планом.

Решение задачи по действиям с краткими пояснениями. Пояснения к каждому из действий формулируются кратко (словосочетанием). После наименования, записанного в круглых скобках, ставится тире, и с маленькой буквы записывается пояснение, в котором заключается основной смысл ответа на поставленный вопрос. (Рис. 7.)

Дети сделали 7 поделок из соломки и 9 поделок из бумаги. На школьную выставку взяли 10 поделок. Сколько поделок осталось?

Решение задачи по действиям с полными пояснениями оформляется следующим образом. (Рис. 8.)

Для детского сада купили 5 ящиков груш по 24 кг в каждом. Из одной шестой части груш сварили компот, а остальные груши раздали детям на полдник. Сколько килограммов яблок раздали детям?

Решение задачи с вопросами. Запись задачи такого типа предполагает постановку вопросов к каждому из действий. Вопрос записывается с большой буквы с начала строки. После него ставится вопросительный знак, а затем с новой строки записывается действие. Порядковый номер действия в этом случае ставится один раз перед вопросом. (Рис. 9.)

На склад привезли 848 мешков крупы. Восьмую долю составила манная крупа, а седьмую долю остатка — гречневая крупа. Сколько мешков было с гречневой крупой?

Решение этой же задачи можно оформить с планом. (Рис. 10.)

В задачах, где при решении необходимо выполнить письменные вычисления, целесообразно решение сразу записывать в столбик. Если решение задачи записывается выражением, при этом необходимо произвести письменные вычисления, они располагаются под выражением.

Наименование пишется после каждого действия задачи или после выражения в скобках с маленькой буквы. В записи наименования допускаются сокращения, по языковым правилам наименование должно оканчиваться на согласный, после которого ставится точка (в случаях, если это сокращение не является общепринятым). В наименованиях, обозначающих единицы измерения длины: мм, см, дм, м, км, единицы измерения веса: г, кг, т, ц, единицы измерения времени: сут, ч, мин, с точки не ставятся.

Слово Ответ записывается с начала строки, после него ставится двоеточие. После двоеточия на первом месте рекомендуется записать результат решения задачи (число), а после него — пояснение к решению. Ответ задачи может записываться как целыми словами, так и с использованием общепринятых сокращений (километров — км, метров — м, километров в час — км/ч и т. п.). Ответ записывается к каждой задаче.

Если задача решается несколькими способами, необходимо записать 1 способ, 2 способ. Ответ в этом случае записывается один раз, как и если решение задачи записано по действиям, а затем выражением.

Если решение задачи выполнялось с полным пояснением, с записью вопросов по действиям, ответ может быть записан кратко. При этом записывается числовое значение и наименование либо число и словосочетание, отражающие ответ задачи. (См. рис. 8–10.)

Если решение задачи записано выражением, по действиям с краткими пояснениями или без них, то ответ задачи должен быть полным (в виде числа и предложения). (См. рис. 5–7.)

При выполнении заданий на нахождение значения математического выражения записи оформляются единообразно. Рассмотрим следующие варианты:

• математическое выражение состоит из одного действия, которое решается устно. Необходимо записать выражение в строку и рядом ответ. При записи нескольких таких выражений между столбиками рекомендуется пропускать в сторону 3 клетки, отсчитывая от самого длинного примера в столбце, а вниз между столбиками — 2 клетки. (Рис. 11.)

• Если для решения математического выражения, которое состоит из одного действия, требуются письменные вычисления, то оно сразу записывается в столбик. В строке можно разместить несколько математических выражений с письменными вычислениями при выполнении условия, что вправо между ними необходимо пропускать не менее 3 клеток. (Рис. 12.)

• На одной строке может размещаться математическое выражение, а рядом с ним — проверка. (Рис. 13.)

• При письменном умноже ии на трёхзначное число следует размещать на одной строке только 2 примера, так как при записи происходит сдвиг влево. (Рис. 14.)

• Если необходимо выполнить несколько примеров на деление многозначных чисел и сделать к ним проверку, на одной строке можно разместить примеры на деление, а под ними проверку. (Рис. 15.)

• При решении математических выражений на порядок действий сначала необходимо записать выражение в строку, затем определить порядок выполнения действий. Записать каждое действие под выражением. Окончательный результат записать в выражение после знака «равно». В случае, если действия предполагают устные вычисления, записывать их не нужно. (Рис. 16, 17.)

Решение уравнения записывается в столбик и включает в себя: уравнение, способ нахождения неизвестного, результат вычисления, проверка решения уравнения. Слова Решение и Проверка не записываются. (Рис. 18.) Уравнения можно записать в столбики, пропустив между ними 3 клетки.

Сравнение чисел. При сравнении двух чисел они записываются на строке с интервалом в одну клетку. В ней учащийся ставит знак. (Рис. 19, пример 1.)

Если число необходимо сравнить с выражением, то в записи между ними оставляется клетка. Знак может быть вставлен только после нахождения значения выражения и сопоставления его с числом. (Рис. 19, пример 2.)

При сравнении двух выражений в записи между ними оставляется клетка. Знак может быть вставлен только после нахождения значений обоих выражений. Найденные значения выражений целесообразно записать на следующей строке и после их сопоставления поставить знак сравнения между ними, а затем на верхней строке в исходном выражении. (Рис. 19, пример 3.)

Сравнение величин требует внимания к единицам их измерения. Если величины выражены в одинаковых единицах измерения, то сравнение производится так же, как и сравнение чисел. Знак ставится между величинами после установления их равенства или неравенства. (Рис. 20, пример 1.)

При сравнении величин, выраженных в разных единицах измерения, необходимо оценить возможность их сравнения без приведения их к единым единицам измерения; если это возможно, поставить требующийся знак. (Рис. 20, пример 2.) Если такой возможности нет, обязательным условием является приведение величин к одинаковым единицам (меньшим или большим). Запись лучше зафиксировать на следующей строке. После сопоставления преобразованных величин можно поставить знак равенства или неравенства и затем перенести его в исходное выражение. (Рис. 20, пример 3.)

При оформлении записи задач геометрического типа чертить фигуру нужно только в том случае, если этого требует условие задачи.

Если задание предполагает только начертить фигуру, от предыдущего задания следует отступить две клетки и начертить заданную геометрическую фигуру.

Если задание предполагает нахождение параметров геометрической фигуры и не предполагает чертёж, то выполнение задания следует оформлять как решение задачи: слово Задача , решение (нахождение параметров геометрической фигуры), Ответ. (Рис. 21.)

Длина прямоугольни ка 16 см, а ширина в 8 раз меньше. Вычислите периметр прямоугольника.

Если задание предполагает нахождение параметров геометрической фигуры и её чертёж, то оформляется это так же, как задача. Сначала проводятся вычисления, затем делается чертёж фигуры с полученными данными. Запись длин сторон фигуры выполняется ручкой. (Рис. 22, 23.)

Оформление чертежа отрезков (рис. 24).

• Начинаем чертить отрезок, отступая от левого края страницы 1 полную клетку.

• Отрезки следует чертить друг под другом, при этом их начальные точки должны находиться на одном расстоянии от левого края страницы.

• Пропуски между отрезками вниз составляют 2 клетки с учётом последующей записи их длины.

• Края отрезков отмечаются небольшими штрихами.

Нахождение значения выражения с переменной записывается следующим образом. (Рис. 25, 26.)

К оформлению контрольных работ предъявляются практически те же требования, что и к классным работам. В случае необходимости учащимися аккуратно делаются исправления на месте допущенных недочётов. Краткая запись к задаче, вопросы, пояснения, которые помогают при обучении решению задач, в контрольной работе не требуются. Формулировки заданий контрольной работы учащимися не переписываются, в тетради ставится порядковый номер выполняемого задания.

Порядок выполнения заданий контрольной работы учащийся может выбрать сам. Записывая решения заданий, необходимо ставить тот порядковый номер задания, под которым оно отмечено в контрольной работе. (Рис. 27.)

В статье освещены отдельные случаи оформления записей по учебному предмету «Математика». Следует отметить, что рекомендации и образцы оформления являются примерными. В случае, если методическим объединением учителей начальных классов разработаны и утверждены локальные нормативные требования к оформлению письменных работ, не противоречащие методическим рекомендациям, а конкретизирующие и уточняющие их, они имеют право быть внедрены в педагогическую деятельность. Основным и важным является требование единообразия оформления записей всеми учащимися.

Без сомнения, соблюдение правил оформления тетрадей на I ступени общего среднего образования способствует воспитанию у учащихся культуры оформления письменных работ и формированию навыков по правильному ведению тетрадей. Однако необходимо помнить, что оформление работ вместе с тем не отражает математической подготовки учащихся. Важно, чтобы записи в учебной тетради учащегося были рациональными, единообразными, экономичными, лаконичными и при этом эстетично оформленными.

Говорим правильно! Или русский язык на уроках математики.

Пихтовникова Светлана Александровна

учитель математики

высшей категории,

заместитель директора МАОУ СОШ № 50

Забота о чистоте, правильности, выразительности речи учащихся всегда была общим делом школьных учителей всех предметов. Традиционно народный учитель в России -носитель высокой культуры, образцовой родной речи: перефразируя известное выражение, можно сказать, что учитель в России — всегда больше, чем учитель.

Роль русского языка в преподавании математики сильно недооценивается, что вызывает серьезное беспокойство.

И именно учителя — начиная с первой учительницы, встретившей ребят на пороге школы, — на протяжении всех школьных лет оказывают определяющее влияние на речевую культуру детей.

В этой общей работе у учителей математики особая роль, особая ответственность. Прежде всего, потому, что учитель математики чаще многих других встречается с детьми и на уроках, и после уроков, беседует с родителями, он почти всегда — классный руководитель, и он часто становится образцом для подражания — ученики непроизвольно копируют речь, манеры, приемы работы своего учителя. Предопределенно такое положение тем, что математика для детей — предмет наиболее трудоемкий, требующий высокого умственного напряжения, и носитель этих знаний — учитель — воспринимается как наиболее умный и осведомленный из всех окружающих.

Большинство учителей математики постоянно следят за правильностью и тонкостью речи учащихся — верным употреблением терминов, склонением числительных, логичностью и доказательностью рассуждений и т. п. Многие рекомендуют детям вести словари — записывать в них новые термины, объяснять смысл пройденных понятий, запоминая одновременно правописание трудных слов. Учителя стараются на уроках давать детям образцы чтения математических предложений, прививают нормы культурного речевого общения.

Однако в речи учителей иногда возникают отклонения от литературных норм. Прежде всего, это связано с тем, что, как и у других профессиональных групп, в учительской среде складывается свой сленг, и он передается от поколения к поколению преподавателей. Кроме того, отклонения от нормативной речи (в том числе орфоэпические ошибки) часто возникают под влиянием окружающей языковой среды — местных диалектов, бытовой речи. Сказывается и недостаточная разработанность речевых нормативов в школьных учебниках математики, в справочной литературе по русскому языку.

Первые шаги в оказании целенаправленной помощи учителю и учащимся в освоении грамотной математической речи предприняты в учебниках математики для 5 и 6 классов авторов Н. Я. Виленкина и др. (издания 1990 — 1998гг.), где введен постоянный раздел «Говори правильно». Но этих материалов явно недостаточно: проблемы с верным чтением выражений, употреблением терминов, постановкой ударений и т. д. возникают постоянно. В дополнение к этим материалам ниже приведены нормативы речи, разъяснения и рекомендации для наиболее типичных «школьных» ситуаций.

ВЫЧЕСТЬ или ОТНЯТЬ? СЛОЖИТЬ или ПРИБАВИТЬ?…

Остановимся на примерах из наиболее ранней математики, где нет еще строгих дефиниций и закордонных терминов, а властвует самый обычный «великий и могучий».

Младшеклассники владеют русским языком может и не слишком грамотно, но достаточно осмысленно. Как они должны воспринимать следующую ситуацию?

«Из двух вычесть три нельзя. Но если у Коли только два яблока, а более сильный Сережка решит отнять у него три, то в результате у Коли не останется ничего, т.е. ноль яблок. А то, что Сережка недополучил, чего хотел, — это уже его, а не Колина проблема. Значит, для Коли 2-3=0. Только ли здесь дело в замене «вычесть» на «отнять»?

Как обычно объясняется равенство«Возьмем яблоко, разрежем пополам, получим две половинки. Если их сложить, то получится что? — Правильно, получится целое яблоко!» Но почему же оно целое, если его только что разрезали? Ведь целое — это неповрежденное. А тут — разрезанное! Значит, целое здесь звучит как-то не по-русски. А как сказать правильно? Или пример не годится? Да и числа складывать нужно не совсем так, как ладошки, т.е. складывать — не прикладывать.

Еще о половинке яблока. Она обычно иллюстрирует вторую половину как результат деления единицы на два, т. е.Но делить яблоко — это значит расчленять, резать его. А

деление единицы на два это уже математическая операция, несовместимая с разрезанием этой единицы. Так какую же смысловую нагрузку несет слово «делить» в подобном объяснении? Ведь операция деления, как обратная умножению, то на этом этапе для дробей пока еще отсутствует. А в арифметическом смысле деление здесь невозможно, о чем долго и упорно детям твердилось: «единица на два не делится», «два на три не делить» (и т. д.). Но даже если подобные «табу» — запреты снять, как же нужно понимать русское слово «делить» при объяснении

На школьном русском математическом языке «умножить на два», умножить (приумножить) в два раза и «увеличить в два раза» — синонимы. Но как свежему (не

математическому) уху воспринимать «умножение в полраза» — как «увеличение враза»?

Рациональные числа вводятся вместе с отрицательными. Но чем минус четыре трети рациональнее двух? В чем тут рационализация? В звучности термина?!

Уже в области дробей школьный русский математический язык начинает заплетаться и запутываться. Слово «отношение», предельно прозрачное в бытовой речи, при введении пропорций расшифровывается на школьном русском математическом языке, как частное от деления двух чисел. Но ранее на том же школьном русском математическом языке частное определялось как результат деления, т. е. число. Значит пропорция — это равенство двух чисел?! Но если два числа равны, то это по сути одно и то же число! Как же теперь с основным свойством пропорции?

В случаях применения пропорций одна из основных задач о дробях (отыскание числа по

дроби) записывается так:При этом в такой задаче число А(=6) является искомым, а

дробью его всегда (подчеркнём — во всех учебниках!) признается 4. Хотя предыдущий

школьный русский математический язык дробью называл

С введением отрицательных чисел школьный русский математический язык становится более интригующим. Как на нём можно пересказать смысл фразы «Жара снизилась с 30° до 25°». Например, так: «температура изменилась на -5°(минус пять градусов). Но тот же школьный русский математический язык объясняет, что -5° и 5° мороза — одно и то же. Получается, что « жара в 30° изменилась на 5° мороза».

Пользуясь синонимами школьного русского математического языка (5=+5), можно исходную мысль выразить и так: «30° жары, изменившись на 5° мороза, превратились в 25° тепла». Если не очень нравится, найдите ошибку. Точно так же в рамках школьного русского математического языка можно сказать, что чайка, летевшая над водой на высоте двадцати метров и изменившая свою высоту на 5 м, оказалась в 15 м над водой.

А можно, умножив долг на долг, получить прибыль?

«Отрицательное время». Имеет ли какой-либо реальный смысл этот набор слов -отрицательное время? В школьном русском математическом языке имеет. В некоторых учебниках такое время рассматривается в порядке комментариев действий с рациональными числами. Но с точки зрения здравого смысла отрицательное время — просто абсурд. В самом деле, если признать, что в какой — то момент время положительно, то и далее оно должно остаться положительным. Ведь оно неумолимо растет. Кто с этим станет спорить? Поскольку данное рассуждение применимо к любому моменту, время всегда положительно. Если же стать на точку зрения авторов отмеченных комментариев, то мы уже сейчас, каждый момент находимся в отрицательном времени. И будем там находиться всю жизнь — ведь для наших дальних потомков все мы окажемся в предпрошедшем времени. Этак легко прийти к выходу, пока мы живем сразу во многих временах, как положительных, так и отрицательных. Как подобный пласт супервиртуальных представлений может переварить не то, что шестиклассник, только начинающий вникать в смысл отрицательного числа, а даже учитель, вроде бы владеющий основами школьного русского математического языка?

Школьный русский математический язык нельзя представить без слов «плюс » и » минус», озвучивающих известные символы. Этим словам особенно не повезло. Разобраться в их смысле в рамках школьного русского математического языка зачастую просто невозможно. Вначале поясним это на слове » минус». Появляется оно первоначально в арифметике при введении вычитания. Далее это слово появляется при озвучивании отрицательных чисел. Затем оно начинает символизировать переход к противоположному числу. Наконец, слово минус возвращается к обозначению вычитания, но уже для чисел, которые сами могут иметь аналогичный знак — символ. В конце концов, не мудрствуя лукаво, автор из школьных учебников начинают придавать этому слову любой (из четырех) удобный для них на текущий момент смысл. Но как же тогда должны осваивать смысл этого слова их ученики? Например, в записи — (-2)=2, получается «минус минус» это «ничего». Здесь уже проявляется способность знака быть невидимкой

Глядя, например, на запись — 2 (минус два), как догадаться, стоит ли (точнее — должен ли стоять) между минусом и двойкой знак плюс, который согласно школьному русскому математическому языку перед числами «обычно опускается» (т.е. не пишется?)?!

Но даже если не углубляться в подобные места, достаточно тонкие с математической и методической точки зрения, то и более поверхностный взгляд на школьный русский математический язык легко обнаруживает ряд его странностей. Заимствуя у русского языка обыденные слов, школьный русский математический язык их делает значительно менее свободными. Малейшая их вариация полностью выбрасывает из них смысл школьного русского математического языка.

Почему числа можно сложить (складывать), но нельзя приложить, уложить, доложить (прикладывать, укладывать, докладывать)? Добавлять, но не убавлять? Число можно умножить, домножить, но не размножить! Можно разделить и даже поделить, но не наделить! Добавить число можно, а вот убавить…!?! Вычислить и зачислить, причислить — какая связь? Считать и читать, подсчитывать и считывать (или подчитывать). Вычитать и дочитать. Почему так разительно меняется смысл?

В бытовой речи приводят кого-то куда-то, подводят кого-то к кому-то. Производят какие-то изделия. А в школьном русском математическом языке приводят подобные члены (куда?), подводят дробную черту, производят умножение и получают произведение.

Можно ли при увеличении получить преувеличение?

Почему в школьном русском математическом языке сомножитель есть, а сослагателя нет? Множители и делители есть, а вычитателя нет? Является ли знаменатель числительным (что числитель есть числительное — здесь всё очевидно)?

СЕЛИ-ЗАПИСАЛИ.

Кто из учителей математики, начиная урок, хотя бы изредка не произносил:

-Здравствуйте. Сели, открыли тетради, записали новую тему.

Такие штампы — с заменой повелительного наклонения («сядьте», «откройте», «запишите» и т.д.) прошедшим временем изъявительного наклонения — сложились во многих школах. Происходит такая замена, начиная с первого класса.

Объяснить использование форм изъявительного наклонения можно, видно, стремлением (часто — неосознанным) к сопричастности, содействию с ребёнком, налаживанию психологического контакта (МЫ записали, МЫ — вместе — начертили и т. д.). Эти высказывания сродни известному докторскому «что У НАС болит?» Кроме того, часто

образовывать форму повелительного наклонения труднее, и здесь у говорящего появляется боязнь ошибиться.

И все же эта замена повелительного наклонения изъявительным грамматически совершенно невозможна, это — серьезная речевая ошибка.

Давайте будем говорить верно:

— Сядьте. Запишите тему урока. Начертите параллелограмм и т. д.

ИКС РАВЕН — ИКС РАВНО.

Многочисленные отклонения от литературной нормы в школьной практике встречаются при чтении выражений с переменными названий функций. Можно услышать, например: «а равен двум», «икс равно восьми», «синус икс равно половине», «логарифм два икс минус пять по основанию три равно единице» и т.п. Остановимся на правилах чтения буквенных выражений.

В русском языке названия латинских букв х, у, z — мужского рода, остальных латинских букв — среднего рода. Надо читать: «а равно трем», «цэ равно минус пяти», но «икс равен тремстам», «игрек равен ста» и т.д.

При чтении выражений названия букв по падежам не изменяются: Зу — «три игрек», а не «три игрека»; 5х — «пять икс», а не «пять иксов».

Если модуль коэффициента отличен от 1; 0,1; 0,01 и т.д., то выражение читают во множественном числе: Зх = 120 — «три икс равны ста двадцати»; 0,8у = -2,4 — «ноль целых восемь десятых игрек равны минус двум целым четырём десятым».

Названия всех греческих букв в математике принято читать в среднем роде, и они, как и названия латинских букв, не изменяются по падежам: «альфа равно тридцати градусам»; «два гамма равны ста восьмидесяти градусам».

(Заметим, что в русском языке названия ряда греческих букв — женского рода и склоняемые; например, вспомним выражение «от альфы до омеги». Но требования точности и однозначности понимания в профессиональной научной речи заставляют отходить от этих общих норм языка.) Ударение в названиях всех греческих букв, кроме омега и омикрон — на первом слоге (альфа, дельта, эпсилон и т.д.). Исключением являются названия: буквы со -«омега», так как оно произошло от выражения «о mega» («о большое», т.е. долгое), и буквы о -«омикрон» (буквально означает «о малое», т.е. краткое).

СИММЕТРИЯ — СИММЕТРИЯ.

Жаркие — даже ожесточённые — споры между учителями возникают о постановке ударений во многих математических терминах, фамилиях учёных. Каждый из спорящих отстаивает «свой» вариант, приводит свои аргументы.

Верная постановка ударения — довольно трудная задача, поскольку в русском языке (в отличие от многих других) ударение бывает подвижно, нет простых однозначных правил «на все случаи». Например, игрА — но Игры, русская фамилия может произноситься ИванОв и ИвАнов, в английском же — ударение всегда на первом слоге (НьЮтон, МАксвелл, НЕпер, ТЕйлор), во французских — на последнем (ДекАрт, ЛопитАль, ВиЕт, ГалУа).

Интересно отметить, что большинство учителей верно называют имена греческих ученых — ЕвклИд, АрхимЕд, ПифагОр, ГерОн и т.д. с ударением на последнем слоге, и только Фалесу «не повезло»: вместо верного ФалЕс (ФалЕс МилЕтский) говорят часто ФАлес.

Ударение в заимствованных из других языков математических терминах (а их -большинство) становится, как правило, в соответствии с принятым в языке-источнике. Вот некоторые примеры: симмЕтрия (греч.) — ось симмЕтрии, центр симмЕтрии, симметричные точки, ассимЕтрия; гомотЕтия (греч.) — центр гомотЕтии, гомотетИчные фигуры, коэффициент гомотЕтии; асимптОта — асимптотический, асимптОта гипЕрболы (допустимо «асИмптота»). В речи многих профессиональных групп некоторые термины произносятся с ударениями, не соответствующими литературной норме (и это считается, видимо, определенным «шиком»). Например, шоферы говорят «искрА» (вместо верного «Искра»), моряки — «компАс» (вместо «кОмпас»), физики-ядерщики — «атОмная» энергия (вместо «Атомная»), «атОмное ядро» и т. д. Похожее положение и с речью профессиональных математиков (колебания в произношении ряда терминов, фамилий иногда свойственны даже определенному ВУЗу или научной школе). Например, «живет» в школах «первообразная функция», хотя верно — «первообрАзная».

ОТРЕЗОЧЕК — УГОЛОЧЕК.

С первых дней пребывания в школе — и даже еще раньше, уже в детском саду — дети постоянно слышат сюсюканье «нежных» воспитателей, учителей: «откройте книжечки», «возьмите цветные карандашики», «съешьте яблочко», «начертите квадратики и кружочки» и т.д. и т.п.

Постоянное и неоправданное использование таких форм существительных (с суффиксами -ик, -ек, -очк, -к) не только неправильно с точки зрения литературных норм языка, но и все время «возвращает» детей (психологически и эмоционально) к младшей возрастной группе (напоминает, что они еще маленькие), а часто и закрепляется в речи самих детей на многие годы (смешно слышать, как уже вполне взрослые девушки и юноши продолжают говорить «кашка», «вкусная котлетка», «закрой окошечко»).

Но если указанные формы существительных хотя бы существуют в языке, и плохо -неумеренное и неуместное их использование, то использование уменьшительно-ласкательных форм в математической речи (и вообще — естественнонаучной) совершенно недопустимо. Однако на уроках часто можно услышать, как и учитель, и дети небольшой отрезок называют -«отрезочек», ребро многогранника — «ребрышко», меньший из нескольких углов — «уголок», чертежный треугольник — «треугольничек», а «под хорошее настроение» — появляются и «интегральчик», и «уравненьице». Следует помнить:

В русском языке у терминов нет уменьшительно—ласкательной формы!

(При этом надо иметь в виду, что в некоторых случаях существительные с суффиксами -ик, -ек, -очк, -к потеряли уменьшительно-ласкательное значение или имеют другой смысл. Поэтому вполне допустимо говорить: «тетрадь в клеточку», «записать в строчку», «записать в столбик» и т.п.).

ОДИН или ЕДИНИЦА?

Часто у учителей математики возникают вопросы, споры — как правильно прочитать такое, например выражение 1 — 0,5:

от одного отнять ноль целых пять десятых или

от единицы отнять ноль целых пять десятых (вариант — из единицы вычесть…)? Название «один» для первого натурального числа часто используется в начальных классах, встречается в названиях чисел. Вспомним: «к одному прибавить три», «от пяти отнять один», «трижды один», «одна целая две десятых» и т.д. Происхождение такого названия понятно — оно связано со счетом предметов: один гриб, два гриба… Этим объясняется и сравнительно большее распространение термина «один» именно в начальной школе — в период освоения понятия числа на базе счета различных предметов, первого знакомства со свойствами ряда натуральных чисел.

В различных математических предложениях чаще используется название единица. Вспомним: «тригонометрическая единица», «единичная окружность», «логарифм единицы» и т. д. Математическая энциклопедия также для первого натурального числа дает только название «единица».

Таким образом, при чтении математических выражений основным является термин единица. Термин же один используется при счете и в названиях чисел. Следует говорить: «один карандаш», «одна целая одна десятая», но «из единицы вычесть ноль целых две десятых», «синус единицы», «единичный отрезок».

СТАМИ? СТА? СТАМЬЮ?

Нет, видимо, в русском языке темы, вызывающей большие трудности, чем тема «Числительные». Редко можно услышать — даже от дикторов радио и телевидения — верно прочитанное многозначное число в косвенном падеже. Неверным чтением выражений с числами грешат иногда и учителя математики.

Такое положение объяснимо: в бытовой речи очень редко склоняют числительные, в начальных классах используют разные «хитрости», позволяющие обходить трудности (например: добавляется слово «число» — «число сто двадцать шесть больше числа сто пятнадцать»; «к тридцати двум прибавляем двадцать восемь и получаем шестьдесят» — вместо «сумма тридцати двух и двадцати восьми равна шестидесяти»; «двадцать три больше, чем пятнадцать» — вместо «двадцать три больше пятнадцати» и т. п.). Таким образом, дети и не слышат образцового чтения числительных от взрослых, и не накапливают собственный речевой опыт.

Неудивительно поэтому, что даже большинство десятиклассников, получив задание просклонять числительное «сто», предлагали в родительном падеже вариант «стам», в творительном — «стами», а один юноша придумал даже вариант «стамью».

К сожалению, на уроках русского языка (тема «Числительные» изучается в 6 классе на полутора десятках занятий) совершенно недостаточно упражнений, времени для освоения темы. И реальную практику в грамотном чтении числительных школьники могут получить только на уроках физики, химии, географии, истории, но в первую очередь, конечно, на уроках математики. Поэтому задача обучения школьников полноценной речи — задача, которую должны решать все учителя: у детей в настоящее время практически нет в их окружении других источников для овладения грамотной речью.

Между тем, правила склонения числительных не так сложны и не постижимы, как может показаться.

НАШ ТРЕУГОЛЬНИК… НАШИ РЕБРА…

Очень часто (особенно — на уроках геометрии) можно услышать и от учителя, и от учеников такие, например высказывания: «наша прямая делит плоскость на две полуплоскости», «углы нашего равностороннего треугольника равны 60», «наш луч делит угол на два равных угла» и, не замечая комизм фраз, в старших классах продолжают: «наши фигуры симметричны и имеют форму квадратов», «наши ребра взаимно перпендикулярны», «наше тело имеет форму цилиндра» и т. п.

Школьный жаргон живуч — эти «накатанные» словосочетания передаются следующим поколениям, попадают даже в некоторые школьные учебники. И мы уже престаем задумываться: почему сказали у нашего равностороннего треугольника такие углы — они ведь у любого другого — «не нашего» — тоже по 60°! Что это за «наша прямая, «наш угол», и т. д.? (Может быть — здесь сказывается наше стремление к приобретательству?)

Безусловно, приведенные примеры — это примеры словесного мусора, которого, к сожалению, немало в профессиональной речи. Надо говорить: «Все углы равностороннего треугольника равны 60°», « построенный луч — биссектриса угла», «данные отрезки параллельны», «ребра куба (а не наши) взаимно перпендикулярны», «рассматриваемый четырехугольник — параллелограмм» и т. п.

В ТЫСЯЧА ДЕВЯТЬСОТ ДЕВЯНОСТО ШЕСТОМ году или В ОДНА ТЫСЯЧА ДЕВЯТЬСОТ ДЕВЯНОСТО ШЕСТОМ году?

Произнося названия числительных, нередко опускают слова «один», «одна». Например, вместо «один миллион, одна тысяча, один миллиард» — читают «миллион, тысяча, миллиард», вместо «одна тысяча девятьсот девяносто шестой» — говорят «тысяча девятьсот девяносто шестой», вместо «один миллион одна тысяча двести пятьдесят» — «миллион тысяча двести пятьдесят».

По нормам русского языка обязательно должно быть четко обозначено начало числа. Поэтому неверно вместо «один миллион двести тысяч» говорить «миллион двести тысяч», а в датах вместо «одна тысяча» — только «тысяча». Однако в середине числа слова «один», «одна» опустить можно: допустимо число 1 001 500тыс. прочитать «один миллиард миллион пятьсот тысяч».

САМЫЙ НАИБОЛЬШИЙ…

В восточной традиции — неумеренное использование в речи превосходных степеней. Помните, в сказках любой шах не просто мудрый, а непременно «наимудрейший»?

В разговорном русском языке, в газетных публикациях в последние десятилетия стала отчетливо проявляться тенденция усиления уже и превосходной степени (мы, таким образом, пошли дальше восточных царедворцев!), неверного образования составной превосходной степени, а часто — и ухода от понимания смысла произносимых слов. Читаем: «покорена самая высочайшая горная вершина», «является наиболее выдающимся нападающим», «самое последнее предупреждение бандитам», «в самое ближайшее время», «самые ужасные впечатления», «не самый худший день», «самый лучший отдых», «самое высшее достижение в спорте», «самый уникальный трюк», а в телевизионном «прямом эфире» услышим и такой шедевр: «Милиции выделяются значительно более меньшие суммы». Послушав внимательно радио- или телевизионные передачи, просмотрев свежую газету, каждый может продолжить этот ряд примеров. Современный журналист, окажись он среди приближенных восточного правителя, обращался бы к нему, наверное, уже «самый наимудрейший» (действительно -наимудрейших ведь пруд пруди!).

Такой стиль речи чужд и современному литературному языку, да и русской традиции. (Однако, в других языках, можно встретиться с похожими явлениями — вспомним, например, вторую форму прошедшего времени для глаголов — Plusquamperfekt — в немецком языке: предпрошедшее, то есть «самое прошедшее» время. Видимо, и для русского языка, кто-то пытается сконструировать «самую превосходную» степень сравнения?)

К сожалению, отмеченная тенденция проявляется и на уровне математики. Можно услышать выражения вроде «самое первое натуральное число», «самое максимальное значение функции», «самое крайнее (или самое последнее) число из числового промежутка», «наиболее прескверный ученик», «самый любимейший предмет» и даже (при исследовании функции) «найдите самое наименьшее или самое наибольшее значение функции».

Рассмотрим ставшее поводом для иронии словосочетание «самый наибольший». На наш взгляд, человек, употребляющий такие выражения, своим школьным учителем математики может лишь гордиться. Дело в том, что, введя в обиход слова наибольшее значение (супремум), максимальное значение, школьные программы и учебники не закрепляют у школьников понимания разницы между локальным и глобальным экстремумом. Исследование на экстремум связывается с использованием производных, что возможно лишь во внутренних точках области определения. Последняя, как правило, не ограничена, вследствие чего граничные значения обычно не обсуждаются. Поэтому выражение «самый наибольший» у человека, далекого от высшего анализа, означает, что максимумов может быть несколько, причем свою мысль он выразил предельно четко. Заметим, что мысль выражена достаточно естественно с позиций здравого смысла. Как вы будете разыскивать самого высокого курсанта во взводе, выстроенном в несколько шеренг? Проще всего — определить самого высокого в каждой шеренге и затем построив их отдельно, выбрать самого наивысокого.

«2-3» — ПО ДВА ВЗЯТЬ ТРИ РАЗА или ПО ТРИ ВЗЯТЬ ДВА РАЗА?

Привычное с детства озвучивание умножения по типу «дважды три» означает присутствие в живом языке элементов математической абстракции. Ведь «дважды три» — это два раза по три (человека, яблока и т.д.), причем два раза — число хоть и именованное, но значительно более отрешенное от предметной сути рассматриваемых объектов (три человека, три яблока…). Таким образом, уже дошкольник, владеющий русским языком, владеет и начальным слоем математической культуры. Тем самым он готов для восприятия более глубоких математических знаний. Но как быть со школьным объяснением выражения «дважды три» — «по два взять три раза» (2+2+2)? Этим выражением у учащихся разбивается уже сложившееся интуитивное представление. Также можно увидеть противоречие в использовании данной фразы и математической записи при введении основ алгебраического языка. Например, если следовать методике преподавания математики в начальных классах, то выражение «4-5» (четырежды пять) следует читать, как «по четыре взять пять раз» (4+4+4+4+4). Тогда как прочитать алгебраическое выражение «4*а»? По четыре взять а раз? Таким образом, получается, что при чтении такой записи приходится нарушать либо интуитивное восприятие данной фразы учащимися, либо методическое правило чтения выражений.

Не логичнее ли уже в начальных классах учить читать выражения так: «четыре раза взять по пять» (5+5+5+5), «четыре раза взять по а» (а+а+а+а)? Таким способом чтения не

нарушается интуитивное представление детей, и не приходится переучивать их в старших классах.

Использование школьного русского математического языка в преподавании математики сходно с ходьбой по тонкому льду. Здесь нужна особая походка, не говоря уже о том, что детей, которых выводят на этот лед, необходимо предупредить: «Осторожно, не поскользнитесь, да и бегать и топать опасно: а вот здесь полынья!» К сожалению, об этих опасностях не подозревают и некоторые поводыри, сами крепко сидящие в таких полыньях. И для детей школьный русский математический язык превращается в коварный и опасный, т.е. совсем недружественный чужой язык.

Почитала , по совместительству мама выпускницы и учитель (не математик), дочь сдавала профиль, физмат класс, учитель-умница, каких мало, подготовка и днем, и ночью, отличный пробник, с экзамена пришла такой, какой я ее никогда не видела.Не хватило времени, даже в туалет не выходила, чтобы не потерять пяти минут, часть с решена частично. Грустно, жаль, что один экзамен решает все. Самооценка ниже ноля.
В то же время, я против отмены ЕГЭ, я за его усовершенствование.
Про профнепригодность, там ниже где-то…Дочь плачет, что ей стыдно перед учителем, как много она в них (учеников своих вложила), а она не смогла. И таких, ответственных и добросовестных учителей, готовящих детей к экзаменам, часто во внеурочное время и в ущерб себе, семье большинство, что бы ни говорили
16.06.2016 23:03:10, logaolga

Пламенный привет учителям математики высшей категории, обучающим вместо математики решению типовых задач, и возрастным психологам по совместительству (а деткам, на минутку, по 18 годков).

А потом удивляются, что на матане либо смертоубийство, либо липа в зачетках.

16.06.2016 13:48:52, OlgaStPb

Я не понимаю такой паники по поводу тригонометрии! У ас в школе все было хорошо с тригонометрией. Я, конечно, не решала сейчас ЕГЭ. Но. думаю, кто готовился и учился, вполне могли бы решить. Я решала всю тригонометрию из Сканави. И как-то нас в школе этому учили, на уроке.
16.06.2016 10:58:16, Милалика13

Спасибо за откровенный рассказ. Теперь понятно, почему ребята наши так расстроены были после профиля.
16.06.2016 03:43:33, мама 11-классника

Ничего не знаю про задания, но то что составители неадекватно оценивают реальность для меня факт. Я все пытаюсь понять их цели. И не могу.
15.06.2016 21:48:55, Кетчуп

Хорошая учительница. Похоже, что права.

Только в наши годы школьный учителя к поступлению в вуз не готовили. Очень крепкую базу давали. Школьный экзамен был немного сложнее первых частей. Я про обычную школу и обычный 10 класс.

Далее подготовка в вуз — сами, сами. Сканави, курсы.
Часть С полностью соответствует вступительному в вуз. Долго мы его писали? Мне кажется, что 4 часа.

15.06.2016 21:42:58, marins

Бог с ними, с заданиями. Меня больше время волнует.
Почему нельзя дать достаточное время, с большим запасом?

Всегда на экзаменах был главный принцип, что времени на решение дают чуть ли не в два раза больше, чем требуется собственно для решения.Эту бОльшую часть времени обычно и тратили на проверку.

А тут гонка. Зачем? Кто не может эти тригонометрические задачи С решить, того лишние два часа не спасут.

С чего вдруг решено, что в институтах должны учиться исключительно холерики с быстрой природной реакцией?
У этого типа темперамента полно недостатков.

15.06.2016 20:49:28, Cat-S

1. Формула приведения логарифма к новому основанию — базовая формула!
2. Как тут правильно написали, в Сканави таких задач полно, решаются они просто( это про 13 тригонометрия с логарифмами).
3. В С части упростили по сравнению с прошлым годом планиметрию и задачу с параметром, усложнили стереометрию.
4. Убрали 2 задачи В части.
Хочу сказать одно. Вместо того, чтобы перекладывать вину на составителей, подумали бы, может это Вы не справились с задачей, не научили детей математике на должном уровне. Все таки это мотивированные дети именно на профильный экзамен.

Нормальный вариант был. Вспомните, в СССР не было никаких ФИПИ и сборников вариантов. Были варианты прошлых лет, явно не в таком кол-ве, и никто не говорил, что в этом году ничего не изменится. Можно было прийти на экзамен и увидеть вместо 5 задач 6 и на порядок сложнее. И поступали не в 5 вузов по 3 специальности, а в один. Получил двойку на экзамене, не прошел по конкурсу — иди гуляй год. Сейчас просто какая то халява, а люди продолжают быть недовольны. Как по мне, надо все усложнять. На всю страну стобалльников должно быть 5 человек, 90 баллов должно быть столько сколько сегодня стобалльников и т.д. Только за все правильные задачи части В надо засчитывать экзамен сданным где-то 11 первичных или 55 тестовых. Если человек не решает эти задачи, ему нечего делать в вузе, где требуют профильную математику.

У меня знакомый доктор наук профессор, когда поступал в МФТИ получил за 4 экзамена 15 из 20 баллов. А сейчас в МФТИ поступают только те у кого 300 из 320 за 3 экзамена по 100баллов максимум, а преподаватели жалуются, на то, что набрали слабый народ. Дети, которые способны нестандартно мыслить при таком раскладе туда не попадают. У них иногда хромает русский ( не 100, а например 87) и делают пару ошибок в физике или математике и все — мимо(

15.06.2016 19:38:43, Маша из Троицка

По пункту 3: я помню, как сама готовилась к поступлению и решала из сборника Сканави эти «тригонометрические уравнения, усложненные логарифмами». И никто тогда их не считал непосильными или «с сюрпризом».
15.06.2016 18:35:29, Arrisha

Показано 102 комментария из 271