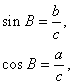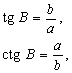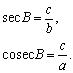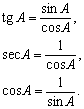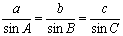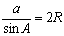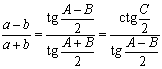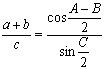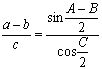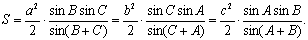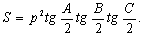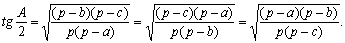Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
В Школе СССР имела статус учебного предмета.
Определение тригонометрических функций
Тригонометрические функции угла θ внутри единичной окружности
Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).
- Синус — отношение противолежащего катета к гипотенузе.
- Косинус — отношение прилежащего катета к гипотенузе.
- Тангенс — отношение противолежащего катета к прилежащему.
- Котангенс — отношение прилежащего катета к противолежащему.
- Секанс — отношение гипотенузы к прилежащему катету.
- Косеканс — отношение гипотенузы к противолежащему катету.
Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до 

- Синус угла
определяется как ордината точки A.
- Косинус — абсцисса точки A.
- Тангенс — отношение синуса к косинусу.
- Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).
- Секанс — величина, обратная косинусу.
- Косеканс — величина, обратная синусу.
Для острых углов новые определения совпадают с прежними.
Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.
История
Древняя Греция
Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.
Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β < α/β < tan α/ tan β, где 0° < β < α < 90°, совместно с другими теоремами.
Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.
Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».
Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93 предложение «Данных» Евклида.
Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха. Ни таблицы Гиппарха, ни Птолемея не сохранились до настоящего дня, хотя свидетельства других древних авторов снимают сомнения об их существовании.
Средневековая Индия
Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
Индийцы также знали формулы для кратных углов 


Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.
Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.
В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.
См. также
- Рациональная тригонометрия
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции
Примечания
- ↑ Советский энциклопедический словарь. М.: Советская энциклопедия, 1982.
«Триггер» перенаправляется сюда. Для использования в других целях, см Триг (значения) .
Тригонометрия (от греческого trigōnon , «треугольника» и Metron , «мера») является ветвью математики , которая изучает взаимосвязь между длинами сторон и углами зрения треугольников . Эта область возникла в эллинистическом мире в III веке до нашей эры из приложений геометрии к астрономическим исследованиям . Греки сосредоточились на вычислении хорд , в то время как математики в Индии создали самые ранние известные таблицы значений тригонометрических отношений (также называемых тригонометрическими функциями ), таких как синус .
На протяжении всей истории тригонометрия применялась в таких областях, как геодезия , геодезия , небесная механика и навигация .
Тригонометрия известна своей индивидуальностью . Эти
тригонометрические тождества обычно используются для переписывания тригонометрических выражений с целью упростить выражение, найти более полезную форму выражения или решить уравнение .
История
Шумерские астрономы изучали измерение углов, используя разделение кругов на 360 градусов. Они, а позже и вавилоняне , изучили отношения сторон подобных треугольников и обнаружили некоторые свойства этих соотношений, но не превратили это в систематический метод нахождения сторон и углов треугольников. В древних нубийцев использовали подобный метод.
В III веке до нашей эры эллинистические математики, такие как Евклид и Архимед, изучали свойства хорд и вписанных углов в окружности, и они доказали теоремы, эквивалентные современным тригонометрическим формулам, хотя они представили их геометрически, а не алгебраически. В 140 г. до н.э. Гиппарх (из Никеи , Малая Азия) дал первые таблицы аккордов, аналогичные современным таблицам значений синусов , и использовал их для решения задач тригонометрии и сферической тригонометрии . Во II веке нашей эры греко-египетский астроном Птолемей (из Александрии, Египет) построил подробные тригонометрические таблицы ( таблицу аккордов Птолемея ) в Книге 1, главе 11 своего Альмагеста . Птолемей использовал длину хорды для определения своих тригонометрических функций, что незначительно отличается от принятого сегодня соглашения о синусе . (Значение, которое мы называем sin (θ), можно найти, посмотрев длину хорды для удвоенного угла интереса (2θ) в таблице Птолемея, а затем разделив это значение на два.) Прошли столетия, прежде чем были составлены более подробные таблицы, и Трактат Птолемея продолжал использоваться для выполнения тригонометрических вычислений в астрономии в течение следующих 1200 лет в средневековом византийском , исламском и, позднее, западноевропейском мирах.
Современное синусоидальное соглашение впервые засвидетельствовано в Сурья-сиддханте , а его свойства были дополнительно задокументированы индийским математиком и астрономом 5-го века (н.э.) Арьябхатой . Эти греческие и индийские труды были переведены и дополнены средневековыми исламскими математиками . К 10 веку исламские математики использовали все шесть тригонометрических функций, составили таблицы своих значений и применяли их к задачам сферической геометрии . Персидский эрудит Насир ад-Дин ат-Туси был описан как создатель тригонометрии как математической дисциплины в своем собственном праве. Насир ад-Дин ат-Туси первым начал рассматривать тригонометрию как математическую дисциплину, независимую от астрономии, и развил сферическую тригонометрию в ее нынешней форме. Он перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии, а в своей работе « На секторной фигуре» сформулировал закон синусов для плоских и сферических треугольников, открыл закон касательных для сферических треугольников и представил доказательства для обоих. эти законы. Знания о тригонометрических функциях и методах достигли Западной Европы благодаря латинским переводам греческого Альмагеста Птолемея, а также работ персидских и арабских астрономов, таких как Аль Баттани и Насир ад-Дин ат-Туси . Одна из самых ранних работ по тригонометрии по северной европейской математике является De Triangulis от немецкого математика 15 — го века Regiomontanus , который поощрял к записи, и снабженный копией Альмагеста , по византийскому греческому ученому кардиналу Виссарион Никейского , с которым он жил на несколько лет. В то же время критский Георгий Трапезундский завершил еще один перевод Альмагеста с греческого на латынь . Тригонометрия была еще так мало известна в Северной Европе 16-го века, что Николай Коперник посвятил две главы De Revolutionibus orbium coelestium объяснению ее основных понятий.
Тригонометрия, движимая требованиями навигации и растущей потребностью в точных картах больших географических областей, превратилась в важный раздел математики. Бартоломей Питискус был первым, кто использовал это слово, опубликовав свою « Тригонометрию» в 1595 году. Джемма Фризиус впервые описала метод триангуляции, который до сих пор используется в геодезической съемке. Это был Leonhard Euler , которые полностью включены в комплексные числа в тригонометрии. Работы шотландских математиков Джеймса Грегори в 17 веке и Колина Маклорена в 18 веке оказали влияние на развитие тригонометрических рядов . Также в 18 веке Брук Тейлор определил общий ряд Тейлора .
Тригонометрические отношения
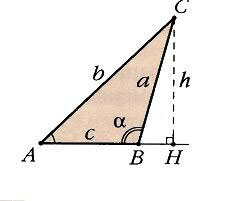
В этом прямоугольном треугольнике: sin A = a / c ; cos A = b / c ; загар А = а / б .
Тригонометрические отношения — это отношения между краями прямоугольного треугольника. Эти соотношения задаются следующими тригонометрическими функциями известного угла A , где a , b и c относятся к длинам сторон на прилагаемом рисунке:
- Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе .
- Функция косинуса (cos), определяемая как отношение соседнего катета (стороны треугольника, соединяющей угол с прямым углом) к гипотенузе.
- Функция касания (тангенс), определяемая как отношение противоположного участка к соседнему участку.
Гипотенузой является стороной , противоположной углом 90 градусов в прямоугольном треугольнике; это самая длинная сторона треугольника и одна из двух сторон , примыкающих к углу А . Смежно нога другая сторона , которая находится рядом с углом А . Сторона , противоположная сторона , которая находится напротив угла А . Термины « перпендикуляр» и « основание» иногда используются для обозначения противоположных и смежных сторон соответственно. См. Ниже в разделе « Мнемоника» .
Так как любые два прямоугольных треугольников с одинаковым острым углом А являются похожи , значение тригонометрического соотношения зависит только от угла A .
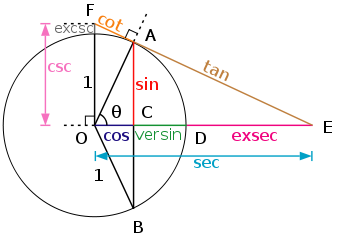
В обратных этих функциях названы косеканс (CSC), секущие (сек) и котангенс (раскладушка), соответственно:
Косинус, котангенс и косеканс названы так, потому что они соответственно являются синусом, тангенсом и секансом дополнительного угла, сокращенного до «со-».
С помощью этих функций можно ответить практически на все вопросы о произвольных треугольниках, используя закон синусов и закон косинусов . Эти законы можно использовать для вычисления оставшихся углов и сторон любого треугольника, если известны две стороны и их угол, или два угла, и сторона, или три стороны.
Мнемоника
Мнемоника обычно используется для запоминания фактов и взаимосвязей в тригонометрии. Например, отношения синуса , косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их и соответствующие им стороны в виде цепочек букв. Например, мнемоника SOH-CAH-TOA:
- S ине = O pposite ÷ Н ypotenuse
- C osine = A djacent ÷ H ypotenuse
- Т angent = O pposite ÷ djacent
Один из способов запомнить буквы, чтобы звук их фонетически (т.е. SOH-CAH-TOA , которое произносится «так KÀ- носком -uh» ). Другой способ заключается в расширении буквы в предложении, такие как « S OMe O LD Н ippie С нечто ругой Н ippie Т rippin’ О п ИДС».
Единичный круг и общие тригонометрические значения
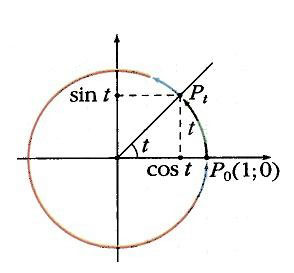
Рис. 1a — Синус и косинус угла θ, определенного с помощью единичной окружности.
Тригонометрические отношения также могут быть представлены с помощью единичной окружности , которая представляет собой окружность радиуса 1 с центром в начале координат на плоскости. В этой настройке конечная сторона угла A, помещенного в стандартное положение, будет пересекать единичный круг в точке (x, y), где и . Это представление позволяет вычислять часто встречающиеся тригонометрические значения, например, в следующей таблице:
Тригонометрические функции действительных или комплексных переменных
Используя единичный круг , можно расширить определения тригонометрических соотношений на все положительные и отрицательные аргументы (см. Тригонометрическую функцию ).
Графики тригонометрических функций
В следующей таблице приведены свойства графиков шести основных тригонометрических функций:
Обратные тригонометрические функции
Поскольку шесть основных тригонометрических функций периодичны, они не инъективны (или 1 к 1) и, следовательно, не обратимы. Однако, ограничив область определения тригонометрической функции, их можно сделать обратимыми.
Названия обратных тригонометрических функций вместе с их доменами и диапазоном можно найти в следующей таблице:
| Имя | Обычное обозначение | Определение | Домен x для реального результата | Диапазон обычного главного значения ( радианы ) | Диапазон обычного главного значения ( градусы ) |
|---|---|---|---|---|---|
| арксинус | у = arcsin ( х ) | х = грех ( у ) | -1 ≤ х ≤ 1 | —π/2≤ y ≤π/2 | −90 ° ≤ y ≤ 90 ° |
| арккозин | у = arccos ( х ) | х = соз ( у ) | -1 ≤ х ≤ 1 | 0 ≤ у ≤ π | 0 ° ≤ y ≤ 180 ° |
| арктангенс | у = арктангенс ( х ) | х = загар ( у ) | все реальные числа | —π/2< у <π/2 | -90 ° < у <90 ° |
| арккотангенс | y = arccot ( x ) | x = детская кроватка ( y ) | все реальные числа | 0 < у < π | 0 ° < у <180 ° |
| арксеканс | y = arcsec ( x ) | х = сек ( у ) | x ≤ −1 или 1 ≤ x | 0 ≤ у <π/2 или π/2< у ≤ π | 0 ° ≤ y <90 ° или 90 ° < y ≤ 180 ° |
| аркосеканс | у = arccsc ( х ) | х = csc ( y ) | x ≤ −1 или 1 ≤ x | —π/2≤ y <0 или 0 < y ≤π/2 | −90 ° ≤ y <0 ° или 0 ° < y ≤ 90 ° |
Представления степенного ряда
Если рассматривать тригонометрические отношения как функции действительной переменной, их можно представить бесконечным рядом . Например, синус и косинус имеют следующие представления:
С помощью этих определений тригонометрические функции могут быть определены для комплексных чисел . При расширении функции действительных или комплексных переменных для комплексной экспоненты справедлива следующая формула :
Эта сложная экспоненциальная функция, записанная в терминах тригонометрических функций, особенно полезна.
Расчет тригонометрических функций
Тригонометрические функции были одними из первых применений математических таблиц . Такие таблицы были включены в учебники по математике, и студентов учили искать значения и как интерполировать между перечисленными значениями, чтобы получить более высокую точность. У правил слайдов были специальные шкалы для тригонометрических функций.
В научных калькуляторах есть кнопки для вычисления основных тригонометрических функций (sin, cos, tan, а иногда и cis и их обратные). Большинство из них позволяет выбирать методы измерения углов: градусы , радианы, а иногда и градиенты . Большинство языков программирования предоставляют библиотеки функций, которые включают тригонометрические функции. Блок с плавающей запятой , оборудование , встроенное в микропроцессорных чипов , используемых в большинстве персональных компьютеров имеет встроенные инструкции для вычисления тригонометрических функций.
Другие тригонометрические функции
В дополнение к шести коэффициентам, перечисленным ранее, существуют дополнительные тригонометрические функции, которые имели историческое значение, хотя сегодня редко используются. К ним относятся аккорд ( crd ( θ ) = 2 sin (θ/2) ) версина ( versin ( θ ) = 1 — cos ( θ ) = 2 sin 2 (θ/2) ) (который появлялся в самых ранних таблицах), покрывающий синус ( охватывает ( θ ) = 1 — sin ( θ ) = versin (π/2— θ ) ) гаверсинус ( haversin ( θ ) =1/2versin ( θ ) = sin 2 (θ/2) ), эксеканс ( exsec ( θ ) = sec ( θ ) — 1 ) и экзосеканс ( excsc ( θ ) = exsec (π/2— θ ) = csc ( θ ) — 1 ). См. Список тригонометрических тождеств для получения дополнительных сведений о взаимосвязях между этими функциями.
Приложения
Астрономия
На протяжении веков сферическая тригонометрия использовалась для определения положения Солнца, Луны и звезд, предсказания затмений и описания орбит планет.
В наше время метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, а также в системах спутниковой навигации .
Секстанты используются для измерения угла наклона солнца или звезд по отношению к горизонту. Используя тригонометрию и морской хронометр , можно определить положение корабля по таким измерениям.
Исторически тригонометрия использовалась для определения широты и долготы парусных судов, построения курсов и расчета расстояний во время навигации.
Тригонометрия по-прежнему используется в навигации с помощью таких средств, как глобальная система позиционирования и искусственный интеллект для автономных транспортных средств .
Геодезия
При топографической съемке тригонометрия используется для расчета длин, площадей и относительных углов между объектами.
В более крупном масштабе тригонометрия используется в географии для измерения расстояний между ориентирами.
Периодические функции
Функция ( выделена красным) — это сумма шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье (выделено синим цветом), которое отображает зависимость амплитуды от частоты , выявляет 6 частот ( в нечетных гармониках ) и их амплитуды ( 1 / нечетное число ).
Функции синуса и косинуса являются фундаментальными для теории периодических функций , например тех, которые описывают звуковые и световые волны. Фурье обнаружил , что каждая непрерывная , периодическая функция может быть описана как бесконечная сумма тригонометрических функций.
Даже непериодические функции могут быть представлены в виде интеграла синусов и косинусов с помощью преобразования Фурье . Это имеет приложения , помимо других областей, в квантовой механике и коммуникациях .
Оптика и акустика
Тригонометрия используется во многих физических науках , включая акустику и оптику . В этих областях они используются для описания звуковых и световых волн , а также для решения проблем, связанных с границами и передачей.
Другие приложения
Другие области, которые используют тригонометрию или тригонометрические функции, включают теорию музыки , геодезию , синтез звука , архитектуру , электронику , биологию , медицинскую визуализацию ( компьютерная томография и ультразвук ), химию , теорию чисел (и, следовательно, криптологию ), сейсмологию , метеорологию , океанографию , сжатие изображений. , фонетика , экономика , электротехника , машиностроение , гражданское строительство , компьютерная графика , картография , кристаллография и разработка игр .
Идентичности
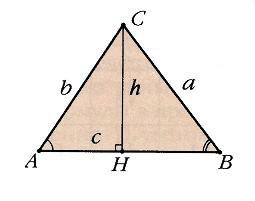
Треугольник со сторонами a , b , c и соответственно противоположными углами A , B , C
Тригонометрия известна своими многочисленными идентичностями, то есть уравнениями, которые верны для всех возможных входных данных.
Тождества, включающие только углы, известны как тригонометрические тождества . Другие уравнения, известные как тождества треугольников , связывают как стороны, так и углы данного треугольника.
Тождества треугольников
В следующих тождествах A , B и C — углы треугольника, а a , b и c — длины сторон треугольника, противоположные соответствующим углам (как показано на диаграмме).
Закон синусов
Закон синусов (также известный как «синус правила») для произвольных состояний треугольника:
где — площадь треугольника, а R — радиус описанной окружности треугольника:
Закон косинусов
Закон косинусов (известно как формула косинуса, или «совы правило») является продолжением теоремы Пифагора на произвольные треугольниках:
или эквивалентно:
Закон касательных
Закон касательных , разработанный Вьют , является альтернативой косинусов при решении по неизвестным краям треугольника, обеспечивая простые вычисления при использовании тригонометрических таблиц. Это дает:
Площадь
Учитывая две стороны a и b и угол между сторонами C , площадь треугольника равна половине произведения длин двух сторон и синуса угла между двумя сторонами:
Формула Герона — еще один метод, который можно использовать для вычисления площади треугольника. Эта формула утверждает, что если треугольник имеет стороны длиной a , b и c , и если полупериметр равен
тогда площадь треугольника равна:
- ,
где R — радиус описанной окружности треугольника.
Тригонометрические тождества
Пифагорейские тождества
Следующие тригонометрические тождества связаны с теоремой Пифагора и верны для любого значения:
Второе и третье уравнения получаются путем деления первого уравнения на и , соответственно.
Формула Эйлера
Формула Эйлера , которая гласит , дает следующие аналитические тождества для синуса, косинуса и тангенса в терминах e и мнимой единицы i :
Другие тригонометрические тождества
Другие часто используемые тригонометрические тождества включают тождества половинного угла, тождества суммы углов и разностей, а также тождества произведения к сумме.
Смотрите также
использованная литература
Библиография
- Бойер, Карл Б. (1991). История математики (второе изд.). ISBN компании John Wiley & Sons, Inc. 978-0-471-54397-8.
- Нильсен, Кай Л. (1966). Логарифмические и тригонометрические таблицы до пяти знаков (2-е изд.). Нью-Йорк: Barnes & Noble . LCCN 61-9103 .
- Терстон, Хью (1996). Ранняя астрономия . Springer Science & Business Media. ISBN 978-0-387-94822-5.
дальнейшее чтение
- «Тригонометрические функции» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Линтон, Кристофер М. (2004). От Евдокса до Эйнштейна: история математической астрономии . Издательство Кембриджского университета.
- Вайсштейн, Эрик В. «Тригонометрические формулы сложения» . MathWorld .
внешние ссылки
- Khan Academy: тригонометрия, бесплатные микролекции онлайн
- Тригонометрия Альфреда Монро Кеньона и Луи Ингольда, компания Macmillan, 1914. На изображениях представлен полный текст.
- Тригонометрическая головоломка Бенджамина Баннекера при конвергенции
- Краткий курс Дэйва по тригонометрии Дэвида Джойса из Университета Кларка
- Тригонометрия, Майкл Коррал, Охватывает элементарную тригонометрию, Распространяется под лицензией GNU Free Documentation License
ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрические функции.
Термин «тригонометрия» ввел в употребление в 1595 немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. К концу 16 в. большинство тригонометрических функций было уже известно, хотя само это понятия еще не существовало.
В тригонометрии выделяют три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т.е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через ее центр. Тригонометрия началась именно с наиболее сложной, сферической части. Она возникла прежде всего из практических нужд. Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звездным небом с незапамятных времен вели и астрологи.
Естественно, все измерения, связанные с расположением светил на небосводе, – измерения косвенные. Прямые могли быть проведены только на поверхности Земли, но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами и тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Аналогичным образом вычисляли и размеры острова в море. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие. Этим и занимается тригонометрия. А поскольку звезды и планеты представлялись древним точками на небесной сфере, то сначала стала развиваться именно сферическая тригонометрия. Ее считали разделом астрономии.
А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.
Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым. Например, 12-я и 13-я теоремы второй книги Начал Евклида (конец 4–3 в. до н. э.) выражают по существу теорему косинусов. Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников. Такие таблицы нужны потому, что значения тригонометрических функций нельзя вычислить по аргументам с помощью арифметических операций. Тригонометрические функции приходилось рассчитывать заранее и хранить в виде таблиц. Гиппарх подсчитал в круге заданного радиуса длины хорд, отвечающих всем углам от 0 до 180°, кратным 7,5°. По существу, это таблица синусов. Труды Гиппарха до нас не дошли, но многие сведения из них включены в Альмагест (II в.) – знаменитое сочинение в 13 книгах греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.). Древние греки не знали синусов, косинусов и тангенсов, вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. В Альмагесте автор приводит таблицу длин хорд окружности радиуса в 60 единиц, вычисленных с шагом 0,5° с точностью до 1/3600 единицы, и объясняет, как эта таблица составлялась. Труд Птолемея несколько веков служил введением в тригонометрию для астрономов.
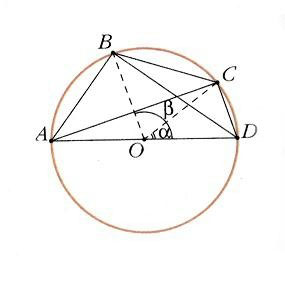
Чтобы понять, как ученые древности составляли тригонометрические таблицы, надо познакомиться с методом Птолемея. Метод основан на теореме – произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений его противоположных сторон.
Пусть ABCD – вписанный четырехугольник, АD – диаметр окружности, а точка O – ее центр (рис. 1). Если известно, как вычислять хорды, стягивающие углы DOC = a и DОВ = b, т. е. сторону СD и диагональ B, то, по теореме Пифагора, из прямоугольных треугольников АDВ и АDС можно найти АВ и АС, а потом, по теореме Птолемея, – BC = (АС·ВD – АВ·СD) /АD, т.е. хорду, стягивающую угол ВОС = b – a. Некоторые хорды, например стороны квадрата, правильных шестиугольника и восьмиугольника, отвечающие углам 90, 60 и 45°, легко определить. Известна также сторона правильного пятиугольника, которая стягивает дугу в 72°. Приведенное выше правило позволяет вычислять хорды для разностей этих углов, например для 12° = 72° – 60°. Кроме того, можно находить хорды половинных углов, однако этого недостаточно, чтобы рассчитать, чему равна хорда дуги в 1°, – хотя бы потому, что все названные углы кратны 3°. Для хорды 1° Птолемей нашел оценку, показав, что она больше 2/3 хорды (3/2)° и меньше 4/3 хорды (3/4)° – двух чисел, совпадающих с достаточной для его таблиц точностью.
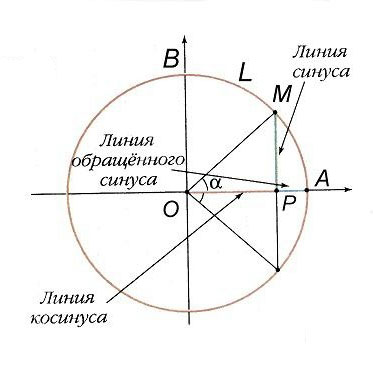
Если греки по углам вычисляли хорды, то индийские астрономы в сочинениях 4–5 вв. перешли к полухордам двойной дуги, т.е. в точности к линиям синуса (рис. 2). Они пользовались и линиями косинуса – вернее, не его самого, а «обращенного» синуса, получившего позднее в Европе название «синус-верзус», сейчас эта функция, равная 1 – cos a, уже не употребляется. Впоследствии тот же подход привел к определению тригонометрических функций через отношения сторон прямоугольного треугольника.
За единицу измерения отрезков MP, OP, PA принималась дуговая минута. Так, линия синуса дуги AB = 90° есть OB – радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18′ = 3438′.
Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4–5 веке н.э.) не столь точны, как птолемеевы; они составлены через 3°45′ (т.е. через 1/24 часть дуги квадранта).
Термины «синус» и «косинус» пришли от индийцев, не обошлось и без любопытного недоразумения. Полухорду индийцы называли «ардхаджива» (в переводе с санскрита – «половина тетивы лука»), а потом сократили это слово до «джива». Мусульманские астрономы и математики, получившие знания по тригонометрии от индийцев, восприняли его как «джиба», а затем оно превратилось в «джайб», что на арабском языке означает «выпуклость», «пазуха». Наконец, в 7 в. «джайб» буквально перевели на латынь словом «sinus», которое не имело никакого отношения к обозначаемому им понятию. Санскритское «котиджива» – синус остатка (до 90°), а на латинском – sinus complementi, т.е. синус дополнения, в 17 в. сократилось до слова «косинус». Наименования «тангенс» и «секанс» (в переводе с латинского означающие «касательная» и «секущая») введены в 1583 немецким ученым Финком.
Большой вклад в развитие тригонометрии внесли арабские ученые, например, Аль-Баттани (ок. 900 н.э.). В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа (940–997), присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся и в наших учебниках. Абу-ль-Вефа устанавливает и основные соотношения между этими линиями.
Итак, к концу 10 в. ученые исламского мира уже оперировали, наряду с синусом и косинусом, четырьмя другими функциями – тангенсом, котангенсом, секансом и косекансом; открыли и доказали несколько важных теорем плоской и сферической тригонометрии; использовали окружность единичного радиуса (что позволило толковать тригонометрические функции в современном смысле); придумали полярный треугольник сферического треугольника. Арабские математики составили точные таблицы, например таблицы синусов и тангенсов с шагом в 1′ и точностью до 1/700 000 000. Очень важной прикладной задачей была и такая: научиться определять направление на Мекку для пяти ежедневных молитв, где бы ни находился мусульманин.
Особенно большое влияние на развитие тригонометрии оказал Трактат о полном четырехстороннике астронома Насир-эд-Дин из Туса (1201–1274), известного так же под именем ат-Туси. Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.
В 12 в. был переведен с арабского языка на латинский ряд астрономических работ, по ним впервые европейцы познакомились с тригонометрией.
Трактат Насир-эд-Дина произвел большое впечатление на немецкого астронома и математика Иоганна Мюллера (1436–1476). Современники больше знали его под именем Региомонтана (так переводится на латинский название его родного города Кенигсберга, ныне – Калининграда). Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятиричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами, а не шестидесятиричными дробями. До введения десятичных дробей оставался только один шаг, но он потребовал более 100 лет. Труд Региомонтана О треугольниках всех родов пять книг сыграл в европейской математике ту же роль, что и сочинение Насир-эд-Дина в науке мусульманских стран.
За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514–1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в1596 его учеником Отто. Углы шли через 10», а радиус делился на 1 000 000 000 000 000 частей, так что синусы имели 15 верных цифр.
Дальнейшее развитие тригонометрии шло по пути накопления и систематизации формул, уточнения основных понятий, становления терминологии и обозначений. Многие европейские математики работали в области тригонометрии. Среди них такие великие ученые, как Николай Коперник (1473–1543), Тихо Браге (1546–1601) и Иоганн Кеплер (1571–1630). Франсуа Виет (1540–1603) дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл «плоскую» теорему косинусов и формулы для тригонометрических функций от кратных углов. Исаак Ньютон (1643–1727) разложил эти функции в ряды и открыл путь для их использования в математическом анализе. Леонард Эйлер (1707–1783) ввел и само понятие функции, и принятую в наши дни символику. Величины sin x, cos x и т.д. он рассматривал как функции числа x – радианной меры соответствующего угла. Эйлер давал числу x всевозможные значения: положительные, отрицательные и даже комплексные. Он также обнаружил связь между тригонометрическими функциями и экспонентой комплексного аргумента, что позволило превратить многочисленные и зачастую весьма замысловатые тригонометрические формулы в простые следствия из правил сложения и умножения комплексных чисел. Он же ввел и обратные тригонометрические функции.
К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника.
Решение любых треугольников, в конечном счете, сводится к решению прямоугольных треугольников (т.е. таких, у которых один из углов – прямой). Поскольку все прямоугольные треугольники с заданным острым углом подобны друг другу, отношения их соответственных сторон одинаковы. Например, в прямоугольном треугольнике ABC отношение двух его сторон, например, катета а к гипотенузе с, зависит от величины одного из острых углов, например А. Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. Всего таких отношений в треугольнике шесть, и им отвечают шесть тригонометрических функций (обозначения сторон и углов треугольника на рис. 3).
Синус 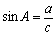
косинус 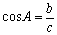
тангенс 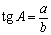
котангенс 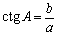
секанс sec A = 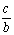
косеканс cosec A = 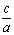
По отношению к углу B («дополнительному» углу по отношению к А) формулы меняются соответственно:
Так как А + В = 90°, то
sin A = cos B = cos (90° – A),
A = ctg B = ctg (90° – A).
Из определений вытекает несколько равенств, связывающих тригонометрические функции одного и того же угла между собой:
С учетом теоремы Пифагора a2 + b2 = c2 можно выразить все шесть функций через какую-нибудь одну.Например, синус и косинус связаны основным тригонометрическим тождеством
sin2A + cos2A = 1.
Некоторые соотношения между функциями:
tg A ctg A = 1,
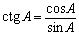
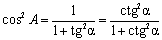
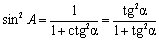
Эти формулы справедливы и для тригонометрических функций любого угла, но ими надо пользоваться осторожно, поскольку правые и левые части могут иметь разные области определения.
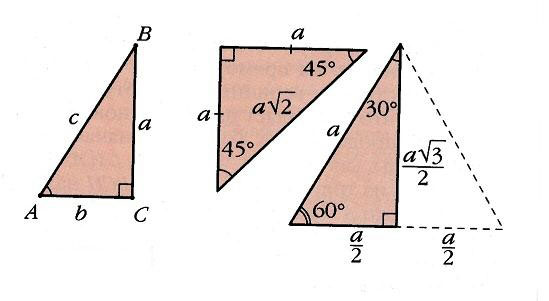
Есть только два прямоугольных треугольника, у которых и углы «хорошие» (выражаются целым или рациональным числом градусов), и хотя бы одно из отношений сторон рационально. Это равнобедренный треугольник (с углами 45, 45 и 90°) и половина равностороннего треугольника (с углами 30, 60, 90°) – как раз те два случая, когда значения тригонометрических функций удается вычислить прямо по определению. Эти значения приведены в таблице
| n | 0 | 1 | 2 | 3 | 4 |
| Угол | 0 | 30° | 45° | 60° | 90° |
| sin | 1 | ||||
| cos | 1 | ||||
| tg | 1 | – | |||
| ctg | – | 1 |

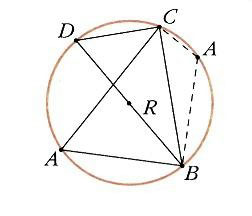
Отношения, входящие в теорему синусов, имеют простой геометрический смысл. Если описать окружность около треугольника ABC (рис. 4) и провести диаметр BD, то по теореме о вписанном угле РBCD = РA либо, если угол тупой, 180° – А. В любом случае a = BC = BD sin A = 2 R sin A или
где R – радиус описанной окружности треугольника АВС. Это «усиленная» теорема синусов, объясняющая, почему таблицы хорд древних были, по существу, таблицами синусов.
Доказывается и теорема косинусов
с2 = а2 + b2 – 2аb cos С.
позволяющая найти сторону треугольника по двум другим сторонам и углу между ними, а также углы по трем сторонам.
Есть и ряд других соотношений между элементами треугольника, например. теорема тангенсов:
называемая также формулой Региомонтана.
Формулы Мольвейде:
Из теорем синусов и косинусов можно вывести (с помощью тригонометрических тождеств) и другие формулы.
Поскольку площадь треугольника S = 1/2 aha = 1/2 bhb = 1/2 chc . Или
= 1/2 ab sin C = 1/2 bc sin A = 1/2 ca sin B;
Но с учетом формулы Герона:
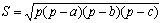
Для вычисления углов по заданным сторонам пользуются формулами:
Радиусы описанной и вписанной окружностей:
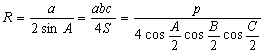
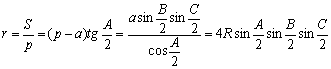
Можно вывести формулы сложения для синусов и косинусов
sin (a + b) = sin a cos b + cos a sin b.
sin (a – b) = sin a cos b – cos a sin b.
Именно эту формулу использовал Птолемей для составления своей таблицы хорд. (Теперь она называется теоремой Птолемея.) Аналогично можно написать формулы косинуса суммы и разности:
cos (a + b) = cos a cos b – sin a sin b,
cos (a – b) = cos a cos b + sin a sin b.
Общее определение тригонометрических функций
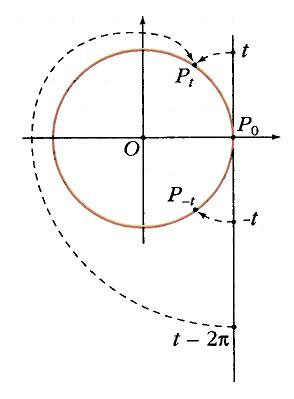
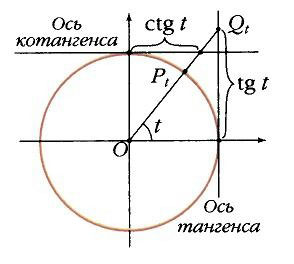
Пусть точка движется с единичной скоростью по единичной окружности с центром в начале координат О против часовой стрелки (рис. 5). В момент t = 0 точка минует P0 (1; 0). За время t точка проходит дугу длиной t и занимает положение Рt, а значит, угол, на который поворачивается луч, проведенный в эту точку из О, тоже равен t. Таким образом, мы сопоставляем каждому моменту времени, т.е. точке t действительной прямой, точку Рtединичной окружности.
Подобное отображение прямой на окружность иногда называют «намоткой». Если представить действительную ось в виде бесконечной нерастяжимой нити, приложить точку t = 0 к точке P0 окружности и начать наматывать оба конца нити на окружность, то каждая точка t попадет как раз в точку Рt. При этом:
1) точки оси, отстоящие друг от друга на целое число длин окружностей, т, е. на 2pk (k =±1, ± 2, …), попадают в одну и ту же точку окружности;
2) точки t и –t попадают в точки, симметричные относительно Ox;
3) при 0 Ј t Ј p угол P0OPtотложен в полуплоскость у і 0 и равен t (рис. 8).
Три этих условия составляют формальное определение такого отображения – намотки. В силу условия 3 при 0 = t Ј p координаты точки р равны (cos t, sin t). Данное наблюдение и подсказывает определение: косинусом и синусом произвольного числа t называются соответственно абсцисса и ордината точки Рt.
Тангенс тоже можно определить через координаты. Проведем касательную к единичной окружности в точке (1; 0) (рис. 7). Она называется осью тангенсов. Точка Qt пересечения прямой OPt с осью тангенсов имеет координаты (1; sin t/cos t), и ее ордината, по определению, равна tg t. По абсолютной величине это длина отрезка касательной, проведенной из Qt к окружности. Таким образом, само название «тангенс» вполне оправдывается. Кстати, как и секанса: на рис. 9 sec t – отрезок OQt, являющийся, правда, не всей секущей, но ее частью. Наконец, котангенс можно определить как абсциссу точки пересечения OPt с осью котангенсов – касательной к единичной окружности в точке (0, 1): ctg t = cos t / sin t.
Теперь тригонометрические функции определены для всех чисел.
Марина Федосова
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
Косинус угла – отношение прилежащего катета к гипотенузе.
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
Рассмотрим прямоугольный треугольник , угол равен

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках и ось в точках и
На данной окружности будет три шкалы отсчета – ось ось и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами – то есть от положительного направления оси против часовой стрелки. Пусть эта точка будет называться (от слова start). Отметим на окружности точку Рассмотрим обозначим его за Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки на ось (точка и на ось игрек (точка

Отрезок является проекцией отрезка на ось отрезок является проекцией отрезка на ось
Рассмотрим прямоугольный треугольник
Поскольку – прямоугольник,
Итак, косинус угла – координата точки по оси (ось абсцисс), синус угла – координата точки по оси (ось ординат).
Давайте рассмотрим еще один случай, когда угол – тупой, то есть больше

Опускаем из точки перпендикуляры к осям и Точка в этом случае будет иметь отрицательную координату по оси Косинус тупого угла отрицательный.
Можно дальше крутить точку по окружности, расположить ее в или даже в четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от до Поэтому мы будем использовать только ту часть окружности, которая лежит над осью (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось и на ось

Координата по оси – косинус угла, координата по оси – синус угла.
Пример:
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Данное тождество – теорема Пифагора в прямоугольном треугольнике

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:
Рассмотрим тупой угол :

Для произвольного тупого угла всегда будут справедливы следующие равенства:
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!




























![Тригонометрия как пишется правильно frac {ab} {a + b} = frac { tan left [ tfrac {1} {2} (AB) right]} { tan left [ tfrac {1} {2} (A + B) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1da4e06eb6f25cd7f7fc1a7784a11a82ae53f9f)