- Статья
- Чтение занимает 4 мин
Это руководство поможет в интерактивном изучении числовых типов в C#. Вы напишете небольшие фрагменты кода, затем скомпилируете и выполните этот код. Руководство содержит ряд уроков, в которых рассматриваются числа и математические операции в C#. В рамках этих занятий вы ознакомитесь с основами языка C#.
Предварительные требования
Для работы с руководством вам потребуется компьютер, настроенный для разработки в локальной среде. В Windows, Linux или macOS для создания, сборки и запуска приложений можно использовать .NET CLI. Для Mac или Windows можно использовать Visual Studio 2019. Инструкции по настройке см. в статье Настройка локальной среды.
Вычисления с целыми числами
Создайте каталог с именем numbers-quickstart. Сделайте его текущим и выполните следующую команду:
dotnet new console -n NumbersInCSharp -o .
Важно!
В шаблонах C# для .NET 6 используются операторы верхнего уровня. Ваше приложение может не соответствовать коду в этой статье, если вы уже выполнили обновление до предварительных версий .NET 6. Дополнительные сведения см. в статье Новые шаблоны C# для создания инструкций верхнего уровня.
Пакет SDK для .NET 6 также добавляет набор неявных директив global using для проектов, использующих следующие пакеты SDK:
- Microsoft.NET.Sdk
- Microsoft.NET.Sdk.Web
- Microsoft.NET.Sdk.Worker
Эти неявные директивы global using включают наиболее распространенные пространства имен для соответствующего типа проектов.
Откройте файл Program.cs в любом редакторе и замените содержимое файла следующим кодом:
using System;
int a = 18;
int b = 6;
int c = a + b;
Console.WriteLine(c);
Чтобы выполнить этот код, введите dotnet run в окно командной строки.
Вы увидели одну из основных математических операций с целыми числами. Тип int представляет целое положительное или отрицательное число или ноль. Для сложения используйте символ +. Другие стандартные математические операции с целыми числами включают:
-— вычитание;*— умножение;/— деление.
Начните с ознакомления с различными операциями. Добавьте следующие строки после строки, с помощью которой записывается значение c:
// subtraction
c = a - b;
Console.WriteLine(c);
// multiplication
c = a * b;
Console.WriteLine(c);
// division
c = a / b;
Console.WriteLine(c);
Чтобы выполнить этот код, введите dotnet run в окно командной строки.
Можно также поэкспериментировать, написав несколько математических операций в одной строке. Например, выполните c = a + b - 12 * 17;. Допускается сочетание переменных и постоянных чисел.
Совет
Вероятнее всего, при изучении C# (как и любого другого языка программирования) вы будете допускать ошибки в коде. Компилятор найдет эти ошибки и сообщит вам о них. Если результат содержит сообщения об ошибках, внимательно просмотрите пример кода и код в окне, чтобы понять, что нужно исправить. Это упражнение поможет вам изучить структуру кода C#.
Вы завершили первый этап. Прежде чем перейти к следующему разделу, переместим текущий код в отдельный метод. Метод — это последовательность инструкций, сгруппированных под одним именем. Чтобы вызвать метод, нужно указать имя метода и () после него. Упорядочение кода в методы упростит работу с новым примером. В результате ваш код должен выглядеть примерно следующим образом:
using System;
WorkWithIntegers();
void WorkWithIntegers()
{
int a = 18;
int b = 6;
int c = a + b;
Console.WriteLine(c);
// subtraction
c = a - b;
Console.WriteLine(c);
// multiplication
c = a * b;
Console.WriteLine(c);
// division
c = a / b;
Console.WriteLine(c);
}
Строка WorkWithIntegers(); вызывает метод. Код после этой строки объявляет метод и определяет его.
Изучение порядка операций
Закомментируйте вызов WorkingWithIntegers(). Это поможет упорядочить выходные данные в этом разделе.
//WorkWithIntegers();
// запускает комментарий в C#. Комментарии — это любой текст, который должен быть сохранен в исходном коде, но не должен выполняться как код. Компилятор не создает исполняемый код из комментариев. Так как WorkWithIntegers() является методом, необходимо закомментировать только одну строку.
Язык C# определяет приоритет математических операций в соответствии с правилами математики. Умножение и деление имеют приоритет над сложением и вычитанием. Убедитесь в этом, добавив следующий код после вызова WorkWithIntegers() и выполнив dotnet run:
int a = 5;
int b = 4;
int c = 2;
int d = a + b * c;
Console.WriteLine(d);
В выходных данных видно, что умножение выполняется раньше сложения.
Можно применить другую последовательность операций. Для этого операции, которые должны выполняться первыми, нужно заключить в скобки. Добавьте приведенные ниже строки и выполните код еще раз.
d = (a + b) * c;
Console.WriteLine(d);
Поэкспериментируйте, объединяя различные операции. Добавьте строки, как показано ниже. Выполните dotnet run еще раз.
d = (a + b) - 6 * c + (12 * 4) / 3 + 12;
Console.WriteLine(d);
Возможно, вы заметили интересное поведение целых чисел. Деление целых чисел всегда дает результат в виде целого числа, даже если ожидаемый результат содержит десятичную или дробную часть.
Если вы еще не видели пример такого поведения, выполните следующий код:
int e = 7;
int f = 4;
int g = 3;
int h = (e + f) / g;
Console.WriteLine(h);
Выполните dotnet run еще раз, чтобы просмотреть результаты.
Прежде чем продолжить, давайте поместив весь код, который вы написали в этом разделе, в новый метод. Вызовите этот новый метод OrderPrecedence. Код должен выглядеть следующим образом:
using System;
// WorkWithIntegers();
OrderPrecedence();
void WorkWithIntegers()
{
int a = 18;
int b = 6;
int c = a + b;
Console.WriteLine(c);
// subtraction
c = a - b;
Console.WriteLine(c);
// multiplication
c = a * b;
Console.WriteLine(c);
// division
c = a / b;
Console.WriteLine(c);
}
void OrderPrecedence()
{
int a = 5;
int b = 4;
int c = 2;
int d = a + b * c;
Console.WriteLine(d);
d = (a + b) * c;
Console.WriteLine(d);
d = (a + b) - 6 * c + (12 * 4) / 3 + 12;
Console.WriteLine(d);
int e = 7;
int f = 4;
int g = 3;
int h = (e + f) / g;
Console.WriteLine(h);
}
Изучение точности и ограничений для целых чисел
В последнем примере вы увидели, что при делении целых чисел результат усекается. Вы можете получить остаток с помощью оператора остатка от деления, который обозначается символом %. Попробуйте выполнить следующий код после вызова метода OrderPrecedence():
int a = 7;
int b = 4;
int c = 3;
int d = (a + b) / c;
int e = (a + b) % c;
Console.WriteLine($"quotient: {d}");
Console.WriteLine($"remainder: {e}");
Тип целых чисел C# характеризуется еще одним отличием от математических целых: тип int имеет минимальные и максимальные ограничения. Чтобы просмотреть эти ограничения, добавьте такой код:
int max = int.MaxValue;
int min = int.MinValue;
Console.WriteLine($"The range of integers is {min} to {max}");
Если при вычислении выводится значение вне этих пределов, возникает условие потери значимости или переполнения. Ответ должен находиться в диапазоне от минимального до максимального значения. Добавьте следующие две строки, чтобы увидеть пример:
int what = max + 3;
Console.WriteLine($"An example of overflow: {what}");
Обратите внимание, что ответ очень близок к минимальному целому числу (отрицательное значение). Он совпадает со значением min + 2. Оператор сложения вызвал переполнение допустимых значений для целых чисел. Ответ является очень большим отрицательным числом, так как переполнение покрывает диапазон от наибольшего целого числа до наименьшего.
Существуют другие числовые типы с различными ограничениями и точностью, которые можно использовать, если тип int не соответствует вашим требованиям. Далее рассмотрим другие типы. Прежде чем перейти к следующему разделу, переместите код, написанный согласно инструкциям из этого раздела, в отдельный метод. Присвойте обработчику события имя TestLimits.
Работа с типом double
Числовой тип double представляет число с плавающей запятой двойной точности. Эти термины могут быть новыми для вас. Число с плавающей запятой можно использовать для представления нецелых чисел, которые могут быть очень большими или малыми. Число двойной точности — это относительный термин, описывающий количество двоичных разрядов, используемых для хранения значения. Числа двойной точности имеют в два раза больше двоичных символов по сравнению с числами одиночной точности. На современных компьютерах числа двойной точности используются чаще, чем одиночной. Числа одиночной точности объявляются с помощью ключевого слова float. Рассмотрим их. Добавьте следующий код и просмотрите результат:
double a = 5;
double b = 4;
double c = 2;
double d = (a + b) / c;
Console.WriteLine(d);
Обратите внимание, что ответ включает десятичную долю частного. Попробуйте более сложное выражение с типом double:
double e = 19;
double f = 23;
double g = 8;
double h = (e + f) / g;
Console.WriteLine(h);
Диапазон значений типа double гораздо больше, чем диапазон значений целых чисел. Добавьте следующий фрагмент после написанного кода:
double max = double.MaxValue;
double min = double.MinValue;
Console.WriteLine($"The range of double is {min} to {max}");
Значения выводятся в экспоненциальном представлении. Число слева от символа E является значащим. Число справа — это показатель степени, который равен 10. Так же, как десятичные числа в математике, значения double в C# могут содержать ошибки округления. Выполните этот код:
double third = 1.0 / 3.0;
Console.WriteLine(third);
Вы знаете, что периодическая десятичная дробь 0.3 не равняется 1/3.
Задача
Выполните другие вычисления с большими числами, малыми числами, умножением и делением с помощью типа double. Попробуйте выполнить более сложные вычисления. После того как вы решите сложную задачу, поместите написанный код в новый метод. Присвойте этому методу имя WorkWithDoubles.
Работа с десятичными типами
Вы уже ознакомились с базовыми числовыми типами в C# — целыми числами и числами типа double. Осталось изучить еще один тип: decimal. Тип decimal имеет меньший диапазон, но большую точность, чем double. Например:
decimal min = decimal.MinValue;
decimal max = decimal.MaxValue;
Console.WriteLine($"The range of the decimal type is {min} to {max}");
Обратите внимание, что диапазон меньше, чем для типа double. Вы можете убедиться в повышении точности при использовании типа decimal, выполнив следующий код:
double a = 1.0;
double b = 3.0;
Console.WriteLine(a / b);
decimal c = 1.0M;
decimal d = 3.0M;
Console.WriteLine(c / d);
Суффикс M возле чисел указывает, что для константы должен использоваться тип decimal. В противном случае компилятор предполагает тип double.
Примечание
Буква M была выбрана потому, что визуально показывает различия между ключевыми словами double и decimal.
Обратите внимание, что при вычислении с использованием типа decimal справа от запятой содержится больше цифр.
Задача
Теперь, когда вы ознакомились с разными числовыми типами, напишите код, который позволяет вычислить площадь круга с радиусом 2,50 см. Помните, что площадь круга равна квадрату радиуса, умноженному на число пи. Подсказка: в .NET есть константа пи Math.PI, которую можно использовать. Math.PI, как и все константы, объявленные в пространстве имен System.Math, — это значение double. По этой причине вместо значений decimal для этой задачи следует использовать double.
Вы должны получить ответ от 19 до 20. Ответ можно просмотреть в готовом примере кода на GitHub.
При желании поэкспериментируйте с другими формулами.
Вы выполнили все задачи краткого руководства по числам в C#. Теперь вы можете выполнить руководство по ветвям и циклам в своей среде разработки.
Дополнительные сведения о числах в C# см. в следующих статьях:
- Целочисленные типы
- Числовые типы с плавающей запятой
- Встроенные числовые преобразования
Число π показывает, во сколько раз длина окружности больше ее диаметра. Неважно, какого размера окружность, — как заметили по меньшей мере еще 4 тыс. лет назад, соотношение всегда остается одним и тем же. Вопрос только, чему оно равняется.
Чтобы высчитать его приблизительно, достаточно обыкновенной нитки. Грек Архимед в III веке до н.э. применял более хитрый способ. Он чертил внутри и снаружи окружности правильные многоугольники. Складывая длины сторон многоугольников, Архимед все точнее определял вилку, в которой находится число π, и понял, что оно приблизительно равно 3,14.
Методом многоугольников пользовались еще почти 2 тыс. лет после Архимеда, это позволило узнать значение числа π вплоть до 38-й цифры после запятой. Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной.
Пока одни ученые использовали геометрический метод, другие догадались, что число π можно рассчитывать, складывая, вычитая, деля или умножая другие числа. Благодаря этому «хвост» вырос до нескольких сотен цифр после запятой.
С появлением первых вычислительных машин и особенно современных компьютеров точность повысилась на порядки — в 2016 году швейцарец Петер Трюб определил значение числа π до 22,4 трлн знаков после запятой. Если напечатать этот результат в строчку 14-м кеглем нормальной ширины, то запись получится немногим короче, чем среднее расстояние от Земли до Венеры.
В принципе ничто не мешает добиться еще большей точности, но для научных расчетов в этом давно нет нужды — разве что для тестирования компьютеров, алгоритмов и для исследований в математике. А исследовать есть что. Даже про само число π известно не все. Доказано, что оно записывается в виде бесконечной непериодической дроби, то есть цифрам после запятой нет предела, и они не складываются в повторяющиеся блоки. Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
Дальнейшие вычисления проводятся в основном из спортивного интереса — и по той же причине люди пытаются запомнить как можно больше цифр после запятой. Рекорд принадлежит индийцу Раджвиру Мине, который в 2015 году назвал на память 70 тыс. знаков, сидя с завязанными глазами почти десять часов.
Наверное, чтобы превзойти его результат, нужен особый талант. Но просто удивить друзей хорошей памятью способен каждый. Главное — использовать одну из мнемонических техник, которая потом может пригодиться и для чего-нибудь еще.
Структурировать данные
Самый очевидный способ — разбить число на одинаковые блоки. Например, можно представить π как телефонную книгу с десятизначными номерами, а можно — как причудливый учебник истории (и будущего), где перечислены годы. Много так не запомнишь, но, чтобы произвести впечатление, хватит и пары десятков знаков после запятой.
Превратить число в историю
Считается, что самый удобный способ запомнить цифры — придумать историю, где им будет соответствовать количество букв в словах (ноль было бы логично заменить пробелом, но тогда большинство слов сольется; вместо этого лучше использовать слова из десяти букв). По этому принципу построена фраза «Можно мне большую упаковку кофейных зерен?» на английском языке:
May — 3,
I — 1
have — 4
a — 1
large — 5
container — 9
of — 2
coffee — 6
beans — 5
На эту тему
В дореволюционной России придумали похожее предложение: «Кто и шутя и скоро пожелает(ъ) Пи узнать число, уже знает(ъ)». Точность — до десятого знака после запятой: 3,1415926536. Но проще запомнить более современный вариант: «Она и была, и будет уважаемая на работе». Есть и стихотворение: «Это я знаю и помню прекрасно — пи, многие знаки мне лишни, напрасны». А советский математик Яков Перельман сочинил целый мнемонический диалог:
— Что я знаю о кругах? (3,1415)
— Вот и знаю я число, именуемое пи — молодец! (3,1415927)
— Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3,14159265359)
Американский математик Майкл Кит и вовсе написал целую книгу Not A Wake, в тексте которой содержится информация о первых 10 тыс. цифр числа π.
Заменить цифры буквами
Кому-то легче запомнить бессвязные буквы, чем случайные цифры. В этом случае цифры заменяются первыми буквами алфавита. Первое слово в названии рассказа Cadaeic Cadenza Майкла Кита появилось именно таким образом. Всего в этом произведении закодировано 3835 знаков числа пи — правда, тем же способом, что в книге Not a Wake.
В русском языке для подобных целей можно использовать буквы от А до И (последняя будет соответствовать нолю). Насколько удобно будет запоминать составленные из них комбинации — вопрос открытый.
Придумать образы для комбинаций цифр
Чтобы добиться по-настоящему выдающихся результатов, предыдущие методы не годятся. Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание.
Допустим, один — это «н», четыре — «р», пять — «т». Тогда число 14 — это «нр», а 15 — «нт». Теперь эти пары следует дополнить другими буквами, чтобы получилось слова, например, «нора» и «нить». Всего понадобится сто слов — вроде бы много, но за ними стоят всего десять букв, поэтому запомнить не так уж сложно.
Число π предстанет в уме как последовательность образов: три целых, нора, нить и т.п. Чтобы лучше запомнить эту последовательность, изображения можно нарисовать или распечатать на принтере и поставить перед глазами. Некоторые люди просто раскладывают соответствующие предметы по комнате и вспоминают числа, разглядывая интерьер. Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа.
Марат Кузаев, Кристина Недкова
Иногда работа с документами в Microsoft Word выходит за пределы обычного написания текста, и может потребоваться, например, записать простое математическое выражение или просто числа, представляющие собой дроби. О том, как это можно делать, расскажем в рамках настоящей статьи.
Написание дробей в Ворде
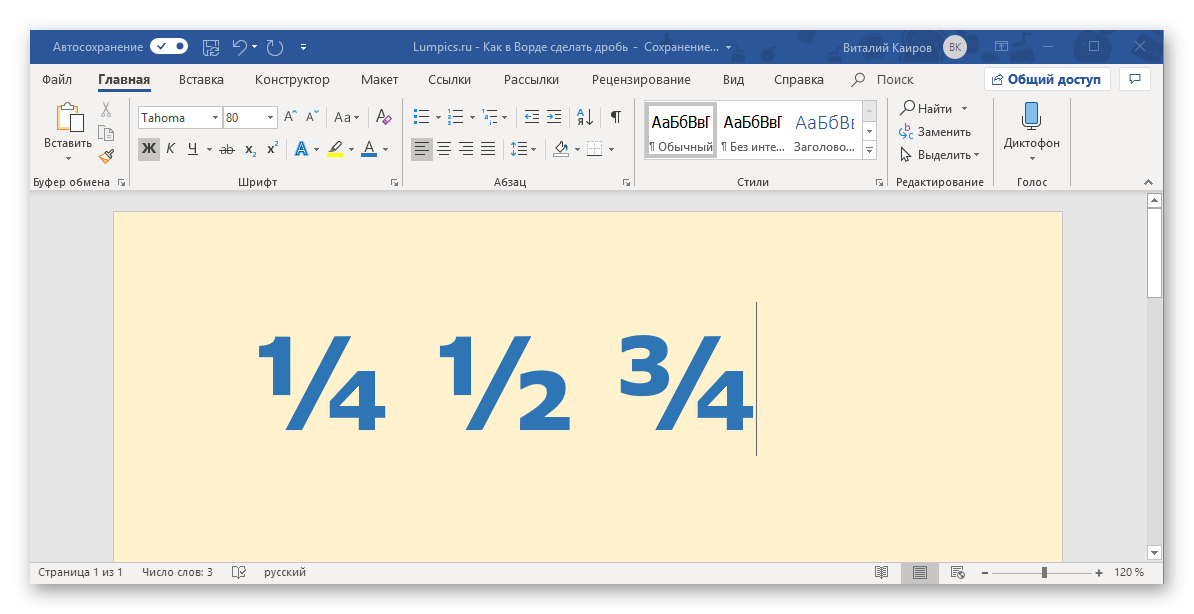
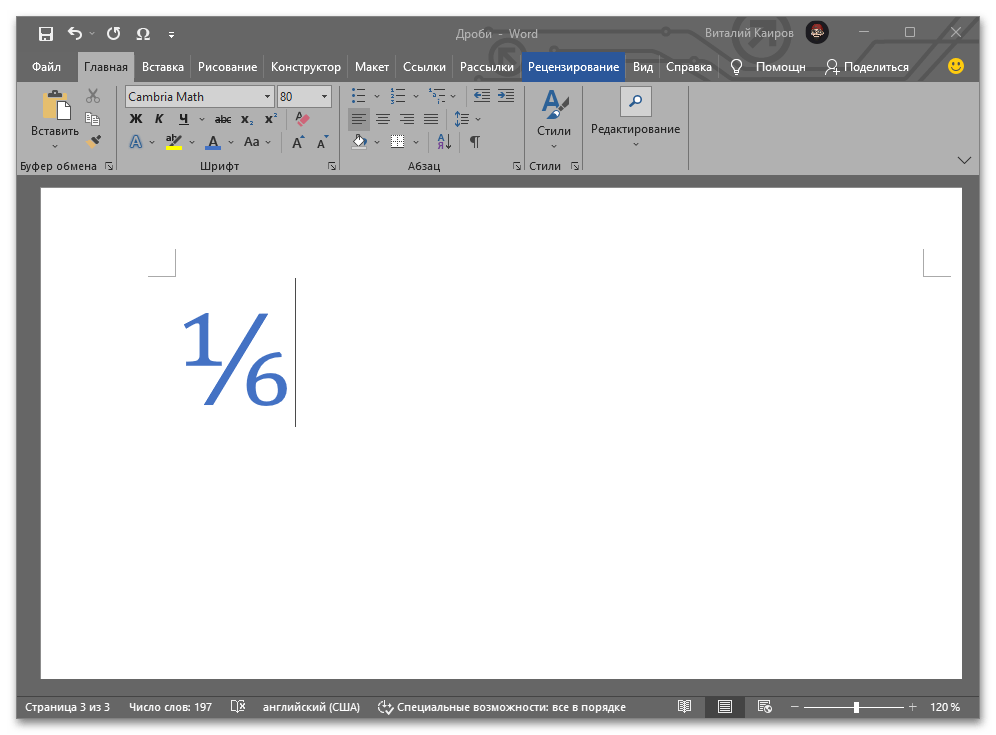
Определенные дроби, введенные вручную, автоматически заменяются в Word на те, которые можно смело назвать правильно написанными. К таковым относятся 1/4, 1/2, 3/4 — после автозамены они приобретают вид ¼, ½, ¾. Однако такие дроби, как 1/3, 2/3, 1/5 и им подобные не заменяются, поэтому должный вид им необходимо придавать вручную.
Стоит отметить, что для написания вышеописанных дробей используется символ «слеш» — / — косую черту, но ведь всех нас еще в школе приучили к тому, что правильное написание дробей — это одно число, расположенное под другим, а разделителем в таком случае выступает горизонтальная линия. Далее мы более подробно рассмотрим каждый из доступных вариантов написания дробей в Ворде.
Вариант 1: Автозамена
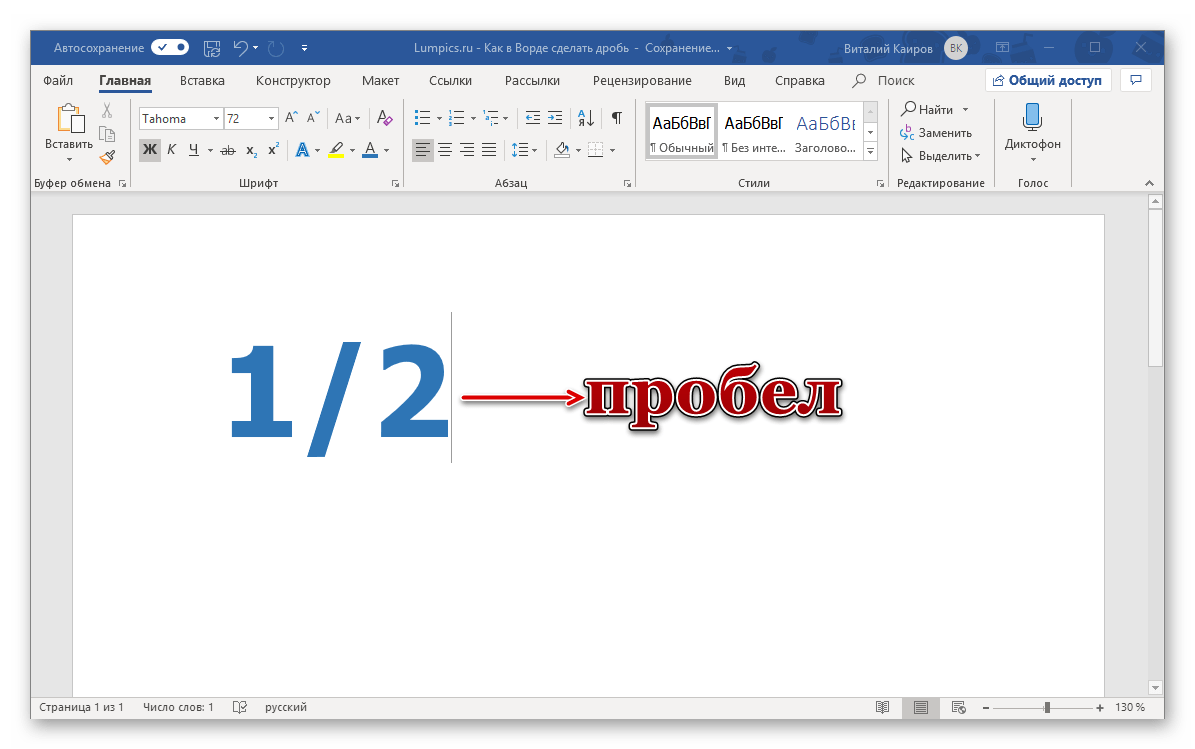
Как мы уже сказали во вступлении, некоторые дроби, записанные через «слеш», Word автоматически заменяет на правильные. То есть все, что от вас требуется в данном случае – написать выражение, а затем нажать на пробел, после чего произойдет автозамена.
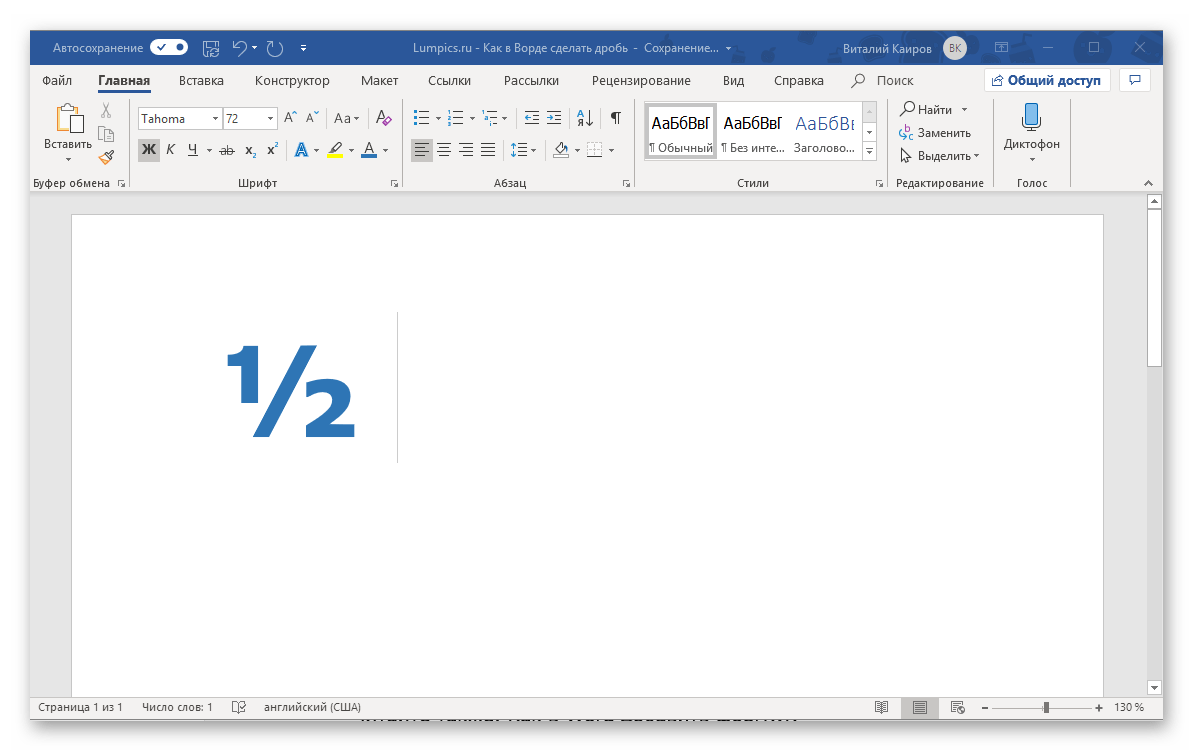
Пример. Пишем 1/2, после чего нажимаем пробел и получаем ½.
Если вы знаете о функции автозамены в Microsoft Word и понимаете принцип ее работы, то наверняка уже догадались, что подобным образом можно настроить замену введенных с клавиатуры числовых символов на «правильные» дроби с разделителем в виде косой черты для всех дробей или хотя бы наиболее часто используемых. Правда, для этого придется обзавестись «источником» этих самых «правильных» записей (расширенный, но все же неполный набор таких символов представлен в Способе 2 части Вариант 2 настоящей статьи).
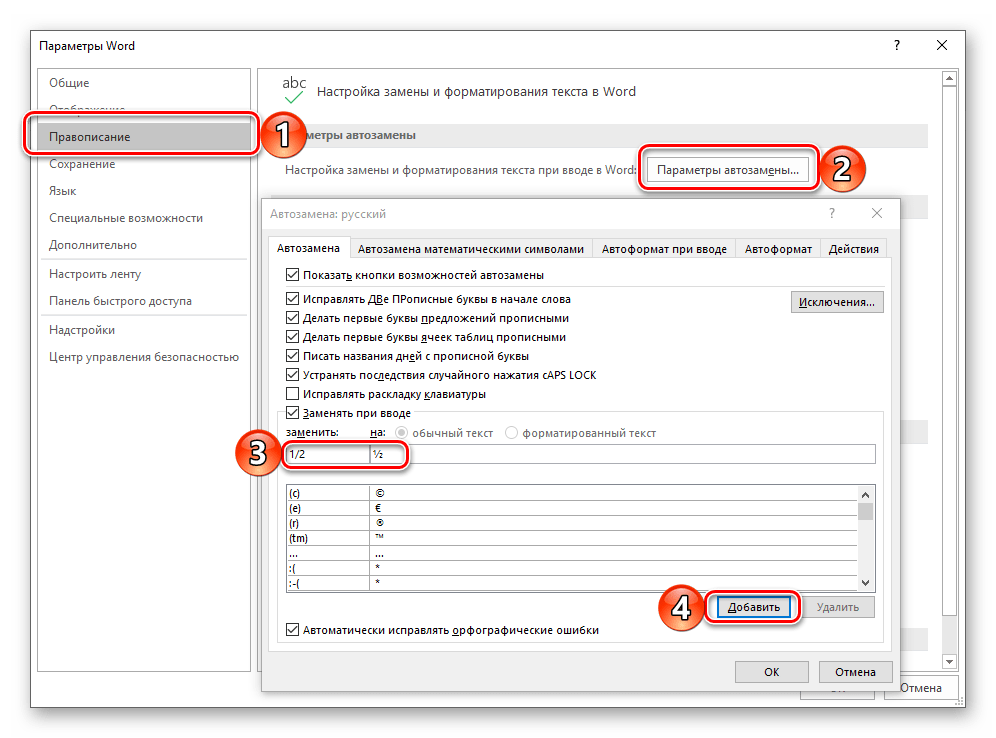
Настроить автоматическую замену можно в разделе «Параметров» текстового редактора. Открыв их, перейдите на боковой панели во вкладку «Правописание» и нажмите по кнопке «Параметры автозамены». В появившемся диалоговом окне в поле «заменить» введите дробь в обычном написании, а в соседнее поле «на» вставьте ее «правильное» написание, после чего воспользуйтесь кнопкой «Добавить». Аналогичное проделайте со всеми остальными дробными выражениями, которые планируете использовать в дальнейшем. Узнать же более подробно о том, что представляет собой автозамена в Ворде, как пользоваться данной функцией и как настроить ее работу под себя, можно в представленной по ссылке ниже статье.
Подробнее: Работа функции «Автозамена» в Word
Вариант 2: Дробь со слешем
Ввести дробь такого вида можно одним из двух методов – посредством вставки доступных в стандартном наборе Ворда символов или использованием соответствующих им кодовых выражений и дополнительных сочетаний клавиш.
Способ 1: Вставка символа
В базовом арсенале Microsoft Word содержится всего шесть знаков дробей со слеш-разделителем. Их добавление осуществляется по следующему алгоритму:
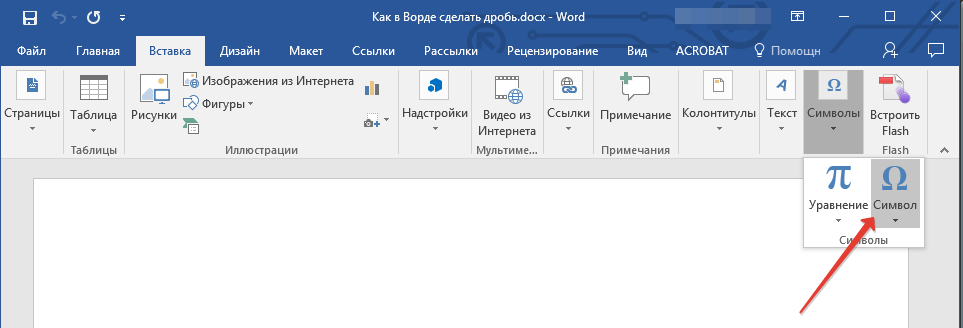
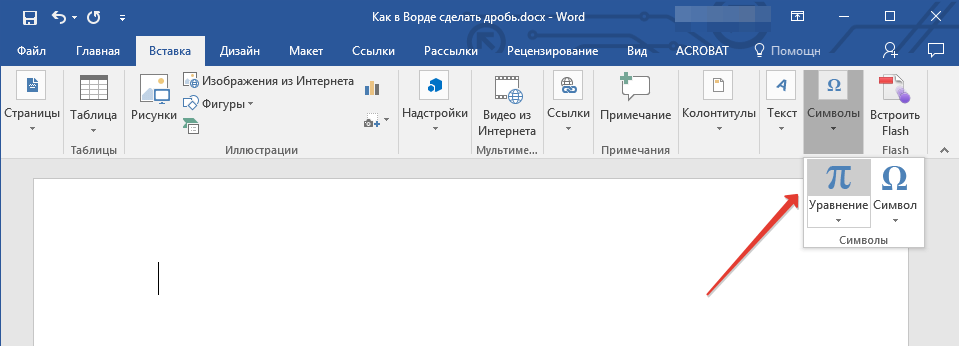
- Откройте вкладку “Вставка”, нажмите на кнопку “Символы” и выберите там пункт “Символы”.
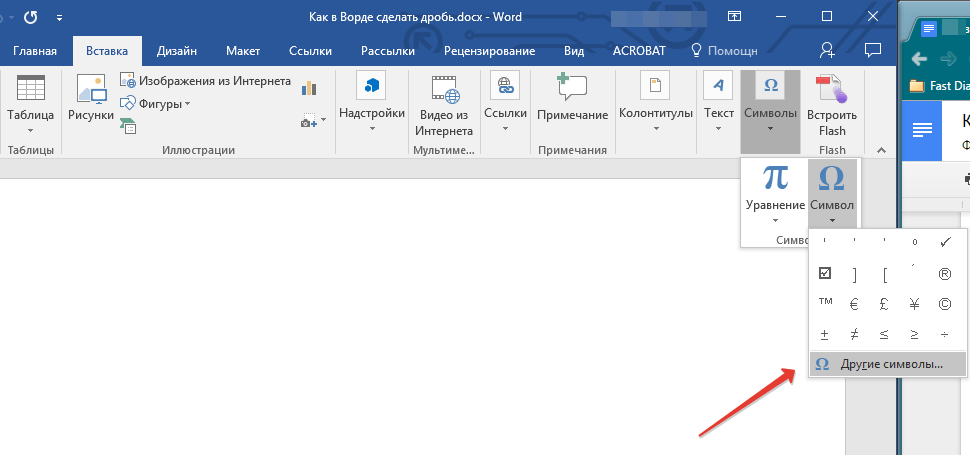
- Нажмите на кнопку “Символ”, где выберите “Другие символы”.
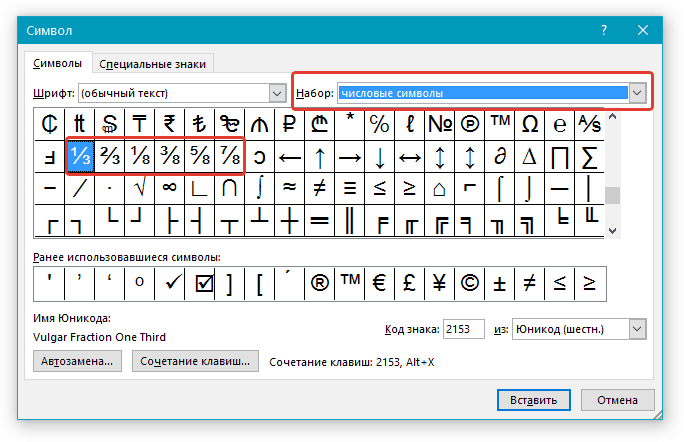
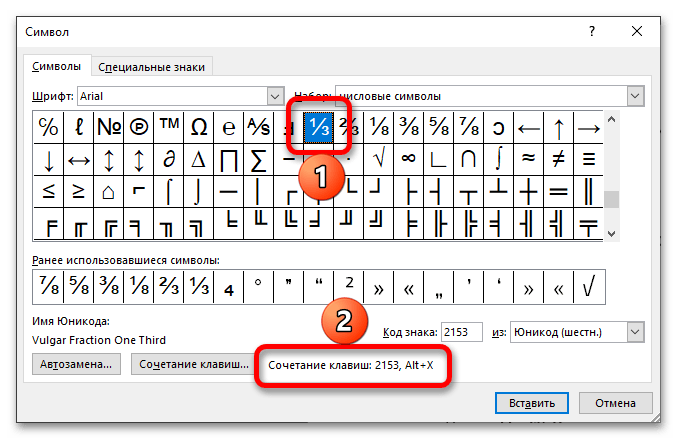
- В окне “Символы” в разделе “Набор” выберите пункт “Числовые формы”.
- Найдите там нужную дробь и кликните по ней. Нажмите кнопку “Вставить”, после чего можно закрыть диалоговое окно.
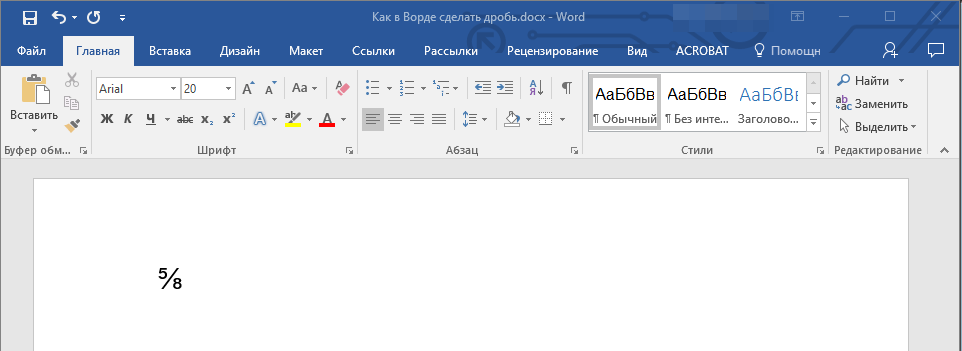
- Выбранная вами дробь появится на листе.
К сожалению, набор шаблонных дробных символов в Ворд тоже весьма ограничен, а потому, если подобная запись должна быть именно с разделителем в виде слеша, оптимальным решением будет настройка функции автозамены, о которой мы рассказали выше, или иной вариации данного метода, о которой пойдет речь далее.
Читайте также: Как вставить галочку в MS Word
Способ 2: Код символа и горячие клавиши
Каждый из доступных для вставки в Ворде символов имеет свой код, который можно преобразовать в необходимые знаки с помощью сочетания клавиш – узнать их можно при выделении соответствующего элемента в окне «Символ».
Так, показанные в предыдущей части статьи дроби, входящие в стандартный набор Microsoft Word, имеют следующие кодовые выражения:
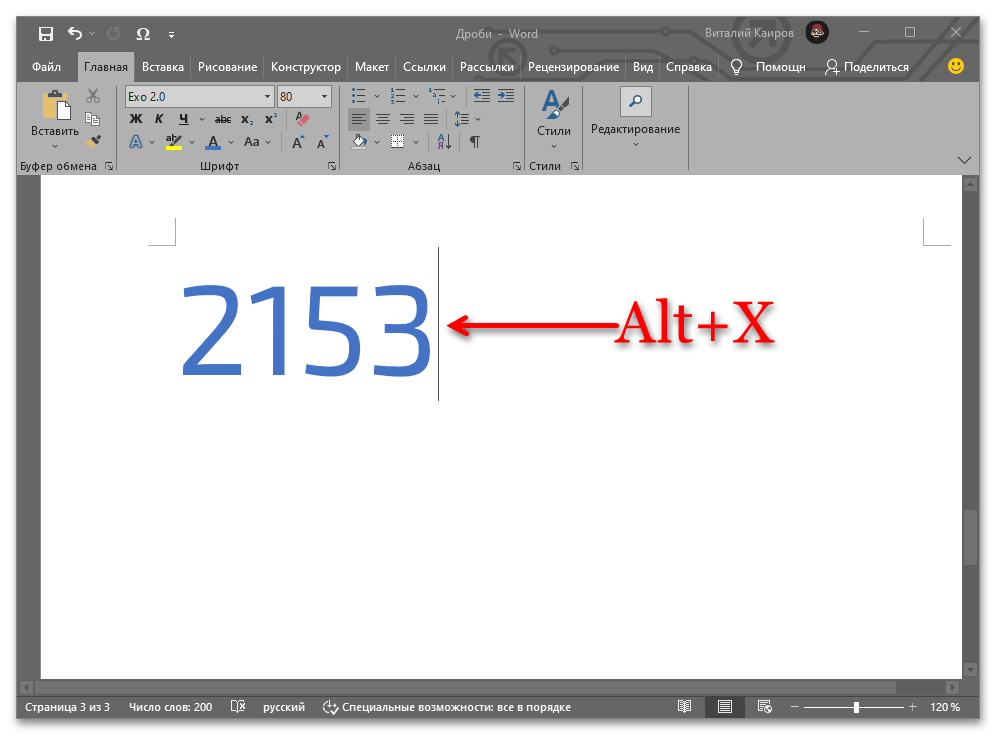
⅓ — 2153
⅔ — 2154
⅛ — 215B
⅜ – 215C
⅝ – 215D
⅞ – 215E
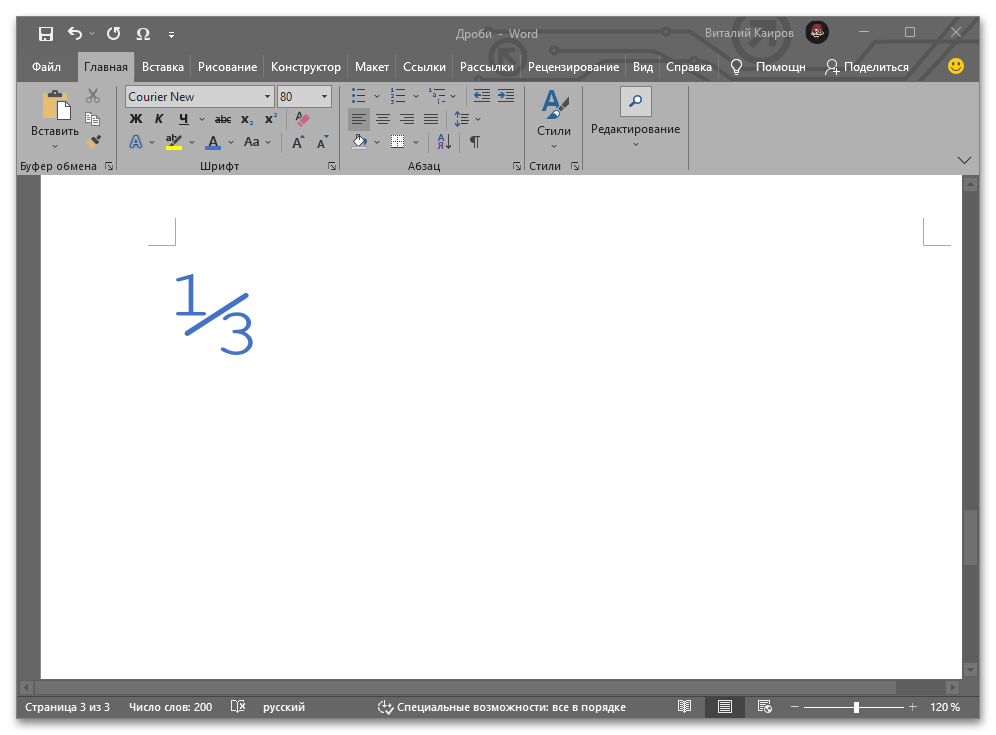
Введите необходимый набор цифр и/или цифр и букву, после чего, не делая отступа, воспользуйтесь клавишами «Alt+X» — код сразу же преобразуется в дробь со слешем.
Несмотря на то что в текстовом редакторе отсутствуют другие дробные знаки, некоторые из них все же можно вставить в документ. Ниже представлен расширенный набор кодовых выражений, преобразовать которые можно тем же сочетанием:
¼ — 00BC
½ – 00BD
¾ – 00BE
⅐ – 2150
⅑ – 2151
⅒ –2152
⅓ – 2153
⅔ – 2154
⅕ – 2155
⅖ – 2156
⅗ – 2157
⅘ – 2158
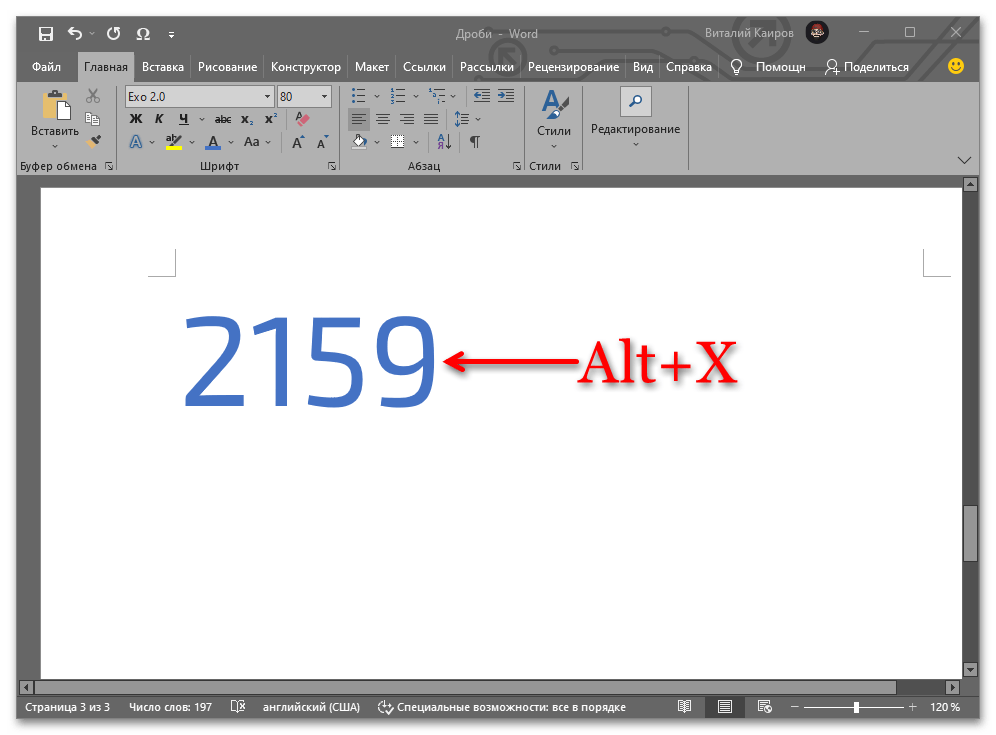
⅙ – 2159
⅚ – 215A
⅛ – 215B
⅜ – 215C
⅝ – 215D
⅞ – 215E
↉ – 2189
Аналогично вышесказанному, для получения любой из указанной выше дробей просто введите соответствующий ей код и затем нажмите «Alt+X».
Например, для получения записи ⅙ следует ввести и преобразовать комбинацией клавиш выражение 2159.
Вариант 3: Дробь с горизонтальным разделителем
Добавить в текстовый документ Ворд дробь с горизонтальным разделителем между числителем и знаменателем можно одним из двух методов – используя средства вставки уравнений или специальный код с его последующим преобразованием.
Способ 1: Вставка формулы
В Microsoft Word имеется набор инструментов для работы с математическими выражениями, для чего можно как использовать уже готовые формулы и уравнения (например, бином Ньютона или площадь круга), так и «собирать» их самостоятельно из более простых записей. В числе последних есть и интересующая нас в рамках настоящей статьи дробь с горизонтальным разделителем.
Читайте также: Как вставить формулу в Ворде
- Откройте вкладку “Вставка” и выберите в группе “Символы” пункт “Уравнение”.
Примечание: В старых версиях MS Word раздел “Уравнение” называется “Формулы”.
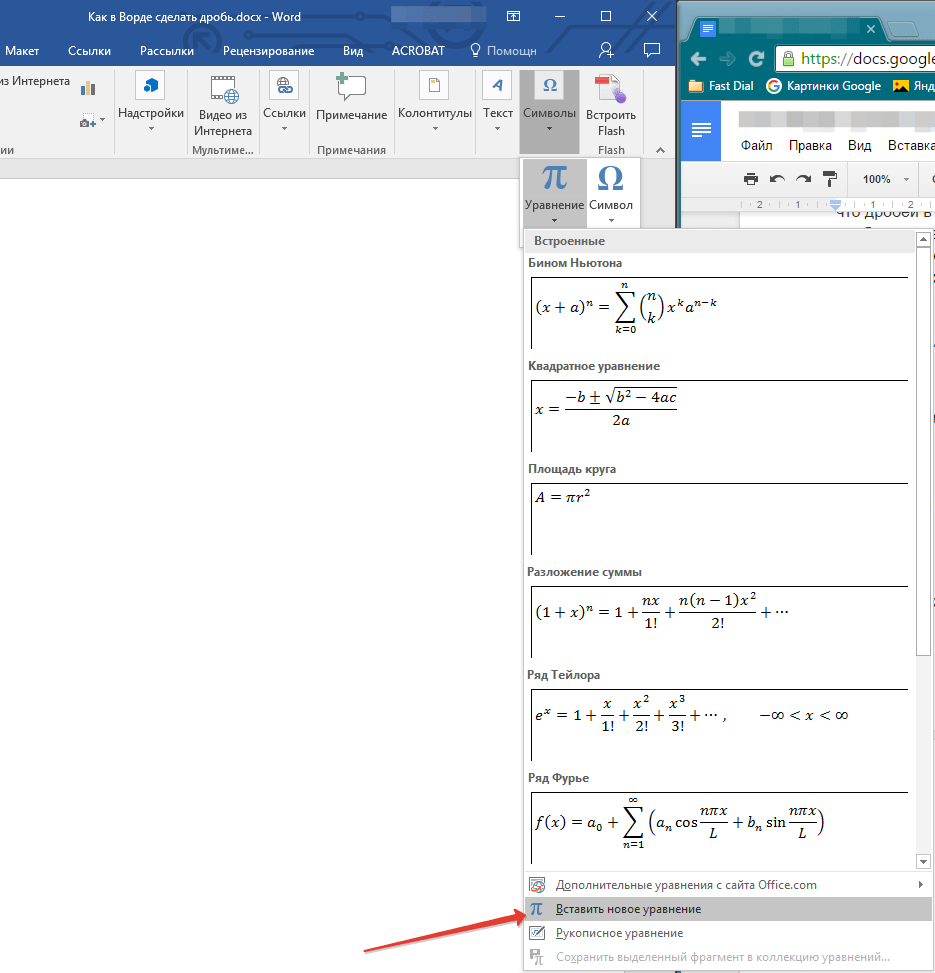
- Нажав на кнопку “Уравнение”, выберите пункт “Вставить новое уравнение”.
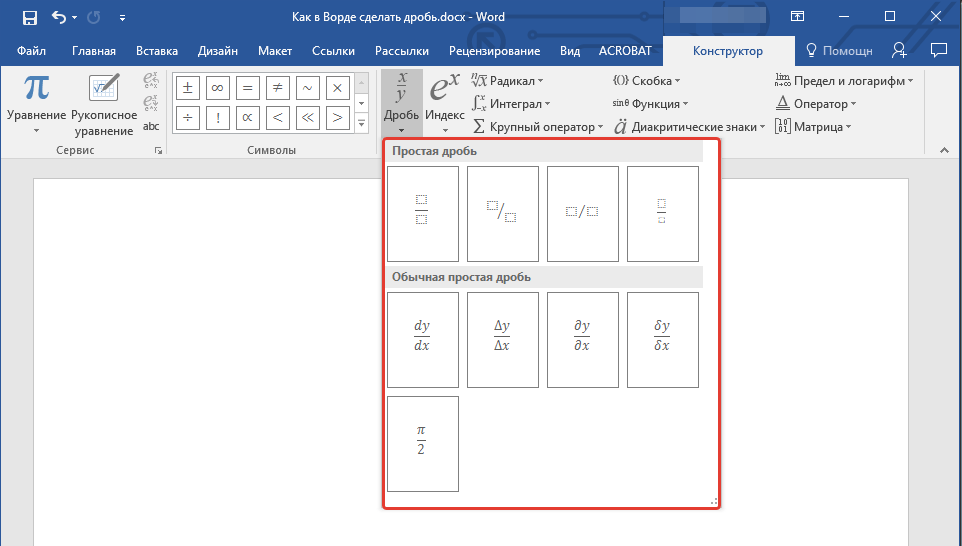
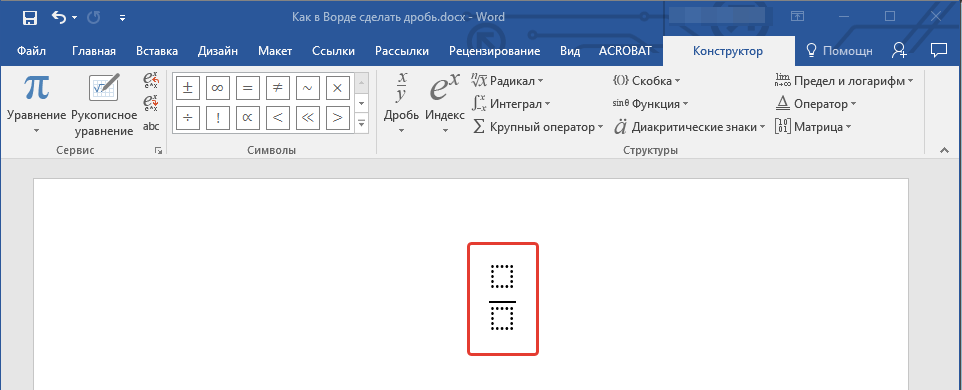
- Во вкладке “Конструктор”, которая появится на панели управления, нажмите на кнопку “Дробь”.
- В развернувшемся меню выберите в разделе “Простая дробь” тип дроби, которую вы хотите добавить — через слеш или горизонтальную линию.
- Макет уравнения изменит свой внешний вид, впишите в пустые графы необходимые числовые значения.
- Кликните по пустой области на листе, чтобы выйти из режима работы с уравнением/формулой.
Именно написание дроби через меню вставки нового уравнения является оптимальным решением нашей сегодняшней задачи, тем более, что таким образом можно добавлять выражения обоих типов — и те, что разделены слешем (косой чертой), и те, которые разделяются горизонтальной полосой. Особенно актуально использование этого метода в случае, когда одними дробями работа не ограничивается и требуется писать и другие математические выражения. Однако есть у такого подхода и недостаток — формулы и их компоненты представляют собой отдельные объекты, для которых доступны далеко не все варианты форматирования (например, нельзя изменить шрифт).
Читайте также: Как изменить шрифт в Word
Способ 2: Коды полей с ключами
Более простой в своей реализации альтернативой предыдущему решению является написание дробей с горизонтальным разделителем путем ввода и преобразования специального кода поля с ключом. Делается это следующим образом:
- Установите указатель курсора в том месте текстового документа, где будет записана дробь.
- Нажмите на клавиши «Ctrl+F9» (обратите внимание, что на ряде ноутбуков, где F-клавиши по умолчанию выполняют мультимедийные функции, дополнительно может потребоваться нажать клавишу «Fn», то есть сочетание в таком случае будет «Ctrl+Fn+F9»).
- В выбранном месте документа появятся фигурные скобки с мигающей между ними кареткой (указатель курсора). Не перемещаясь из этой области, введите код следующего вида:
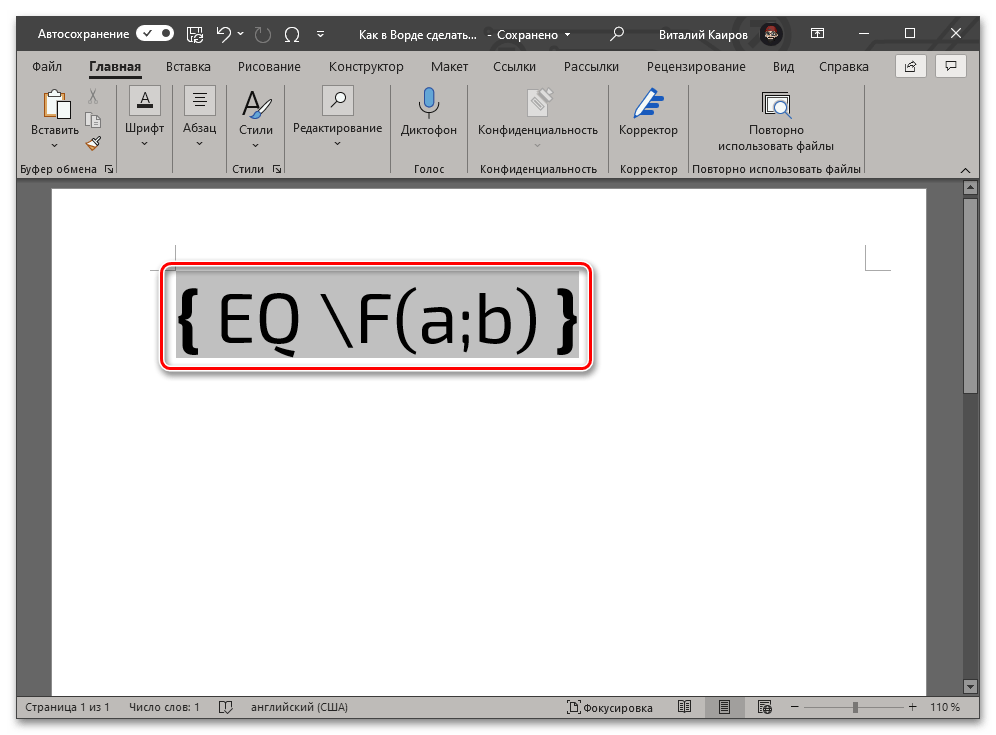
EQ F(a;b)- EQ создает поле для ввода формулы;
- F создает дробь с горизонтальным разделителем и выравнивает относительно этой линии числитель и знаменатель;
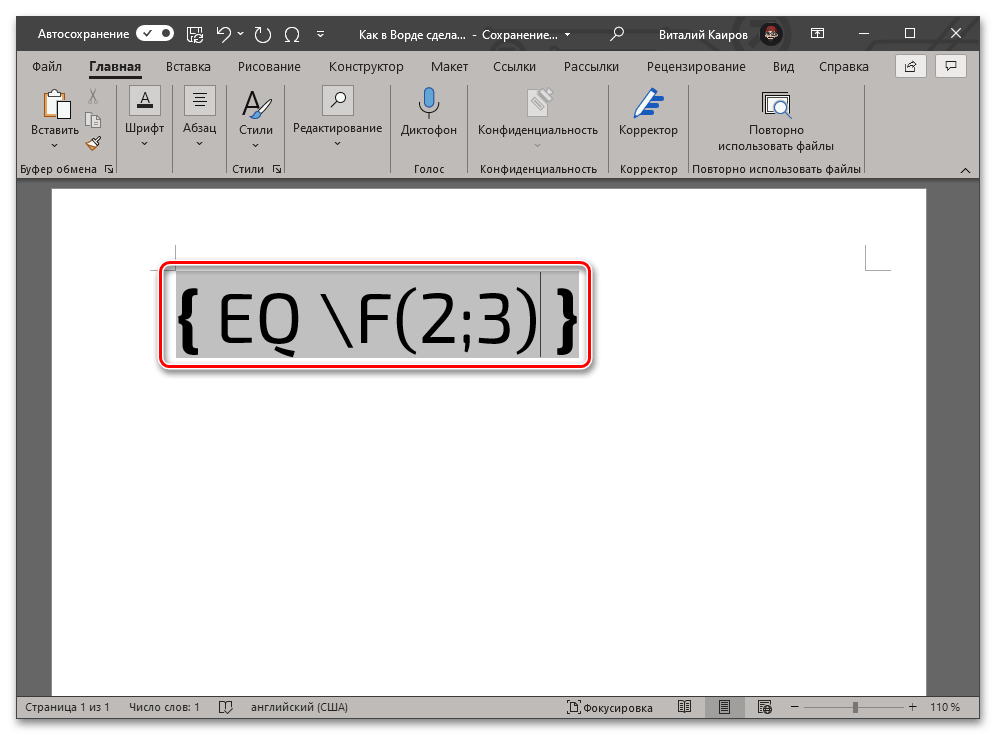
- a и b – числитель и знаменатель, то есть вместо этих букв нужно вводить соответствующие им значения. Например, чтобы записать таким образом 2/3, следует использовать указанный ниже код:
EQ F(2;3)Обратите внимание! В случае если вами используется локализованная версия операционной системы, а в качестве десятичного разделителя в ней выступает запятая, между числителем и знаменателем в скобках необходимо вводить точку с запятой, как это показано в примерах выше. То есть именно это решение применимо в абсолютном большинстве случаев. Однако если разделителем в ОС является точка (это характерно для англоязычных версий), между числителем и знаменателем потребуется ставить запятую.
- Разобравшись со всеми параметрами кода и указав его в том виде, который соответствует желаемой дроби, не перемещая указатель курсора и не покидая обозначенное фигурными скобками поле для ввода, нажмите на клавишу «F9» (опять же, на ноутбуках может потребоваться нажать «Fn+F9»).
Читайте также: Как поставить фигурные скобки в Майкрософт Ворд
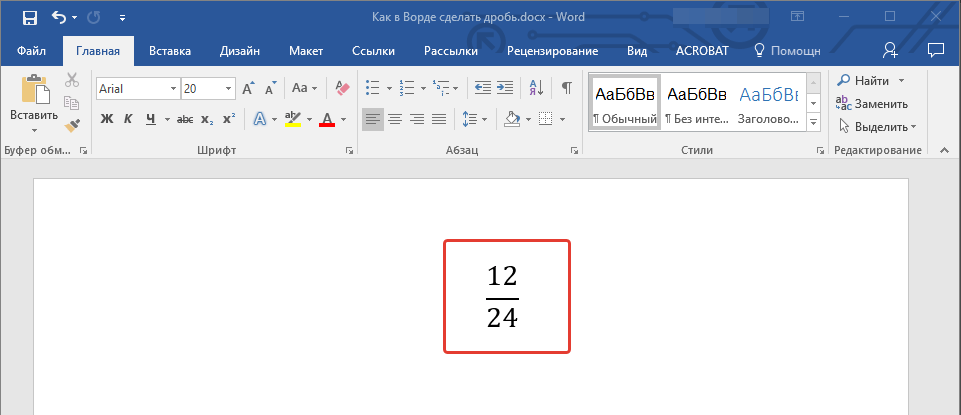
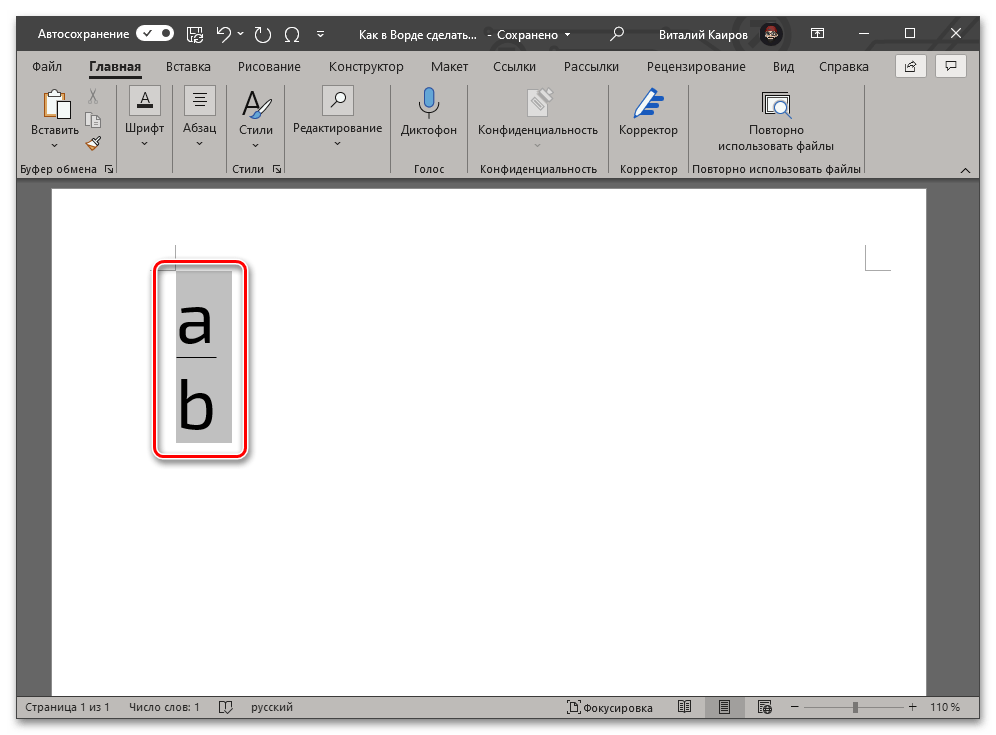
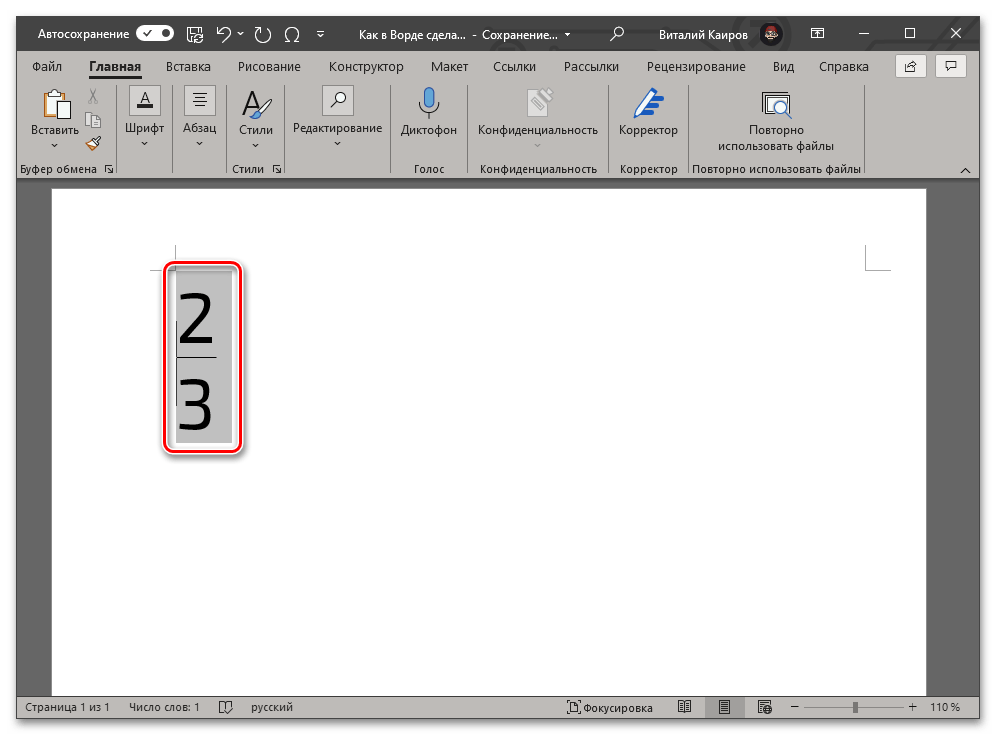
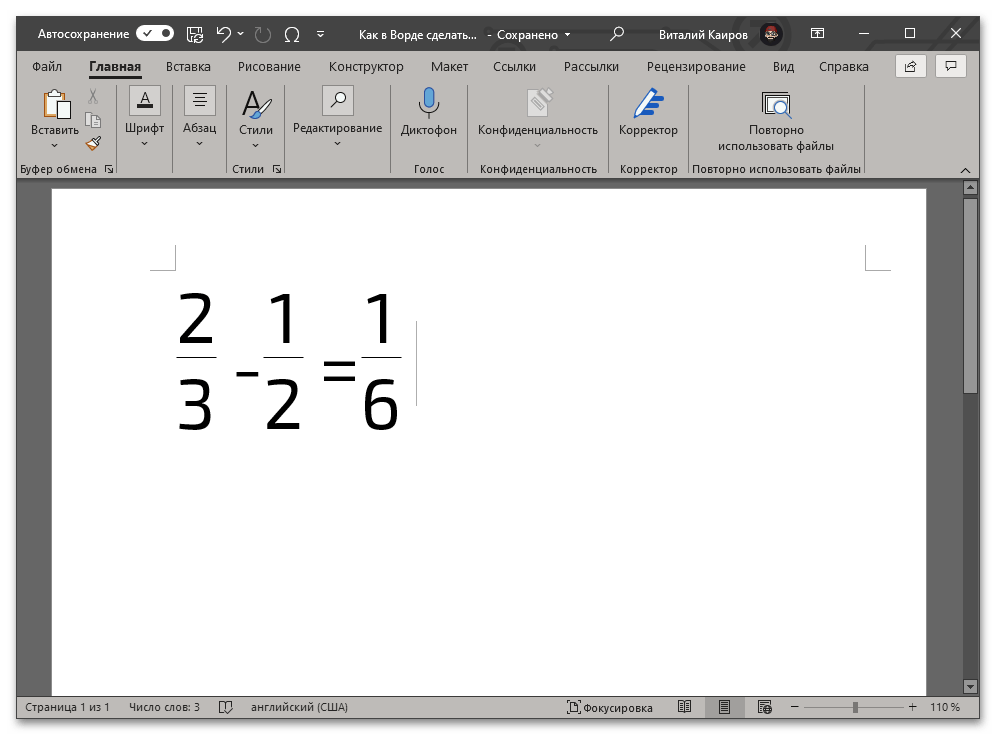
- В результате выполнения предыдущего шага инструкции код будет преобразован в дробь с горизонтальным разделителем между числителем и знаменателем, что показано на представленных выше и ниже изображениях.
Этот метод является не только более простым и удобным в своем реализации, чем предыдущий, но и лишен характерных для него ограничений. Так, у записанной дроби отсутствует видимое поле (рамка), она выглядит более эстетично и является пригодной для общего форматирования, представляется в виде используемого по умолчанию для ввода текста шрифте, который по необходимости можно изменить на любой другой.
Читайте также: Как форматировать текст в документе Word
Заключение
Из этой небольшой статьи вы узнали, как сделать дробь в текстовом редакторе Ворд любых версий. Как видите, данную задачу можно решить несколькими способами, а инструментарий программы еще и позволяет автоматизировать ее выполнение.


Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ