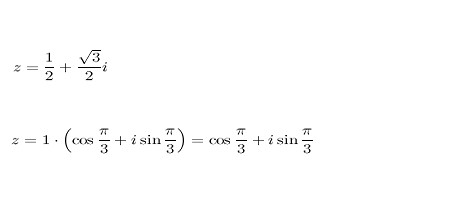Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.
Возведение в произвольную степень на Паскале
Требуется вычислить значение с = ab. В зависимости от значений
основания a и показателя степени b,
вычисление степени может быть реализовано по-разному.
Если a > 0, а b может принимать произвольные вещественные значения, используем известную формулу
ab = exp (b * ln a):
c:=exp(b*ln(a));
Если b — целое число (вообще говоря, «не слишком большое» по модулю),
а a — любое (не равное нулю при b < 0),
возведение в степень может быть реализовано с помощью цикла:
var i:integer;
{...}
c:=1;
for i:=1 to abs(b) do c:=c*a; {перемножение одинаковых сомножителей b раз}
if b<0 then c:=1/c; {учёт знака показателя} Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:
c:=exp(b*ln(abs(a))); {степень положительного основания}
if (odd(b)=true) and (a<0) then c:=-c; {если основание отрицательно, а показатель нечетный, то меняем знак} Вычисление корня произвольной степени на Паскале
Стандартная функция sqrt умеет извлекать только квадратный корень.
Извлечь корень степени n (где n — натуральное)
из числа a можно всегда, кроме случая, когда a < 0
и при этом n четно. Извлечь корень степени n
из числа a означает возвести число a в степень 1/n.
При этом знак корня совпадает со знаком a.
Ниже приводится код функции, вычисляющей корень произвольной степени
n от своего аргумента a:
function root(a:real;n:word):real;
{Тип word здесь указывает, что n положительно}
var r: real;
begin
r:=exp(ln(abs(a))/n); {корень из модуля}
if a<0 then root:=-r else root:=r {учет знака}
end;
Вычисление логарифмов на Паскале
Стандартная функция ln вычисляет только натуральный логарифм.
Для вычисления логарифмов по другим основаниям можно применить формулу
log a b = ln b / ln a:
c:=ln(b)/ln(a);
В частности, для вычисления десятичного логарифма lg b можно записать:
c:=ln(b)/ln(10);
Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале
В Паскале имеется стандартная функция arctan для вычисления арктангенса.
Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.
Для вычисления y = arcsin x, где, конечно, |x| <= 1,
можно применить один из следующих способов:
if x=1 then y:=pi/2 else if x=-1 then y:=-pi/2 else y:=arctan(x/sqrt(1-sqr(x)));
или
y:=2*arctan(x/(1+sqrt(1-sqr(x))));
на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).
Для вычисления z = arccos x, где |x| <= 1,
можно использовать тот факт, что
сумма арксинуса и арккосинуса некоторого значения
равна прямому углу:
if x=1 then z:=0 else if x=-1 then z:=pi else z:=pi/2-arctan(x/sqrt(1-sqr(x)));
или
z:=pi/2-2*arctan(x/(1+sqrt(1-sqr(x))));
Вычисление полярных углов на Паскале
Полярным углом точки с координатами (x,y),
отличной от начала координат,
называют угол между положительным направлением оси Ox и
направлением из начала координат на данную точку. При этом угол
отсчитывается против часовой стрелки.
Строго говоря, полярный угол не всегда
равен arctg (y/x), это верно лишь при x > 0.
Кроме того, при делении большого значения y на малое x
возможно переполнение. Показанная ниже функция вычисляет полярный угол fi,
лежащий в промежутке от -pi до +pi,
для любой точки с координатами (x,y), не совпадающей с началом координат:
function fi(x:real; y:real):real; var f:real; begin if abs(x)>abs(y) then begin f:=arctan(y/x); if x>0 then fi:=f else if y>=0 then fi:=f+pi else fi:=f-pi end else begin f:=arctan(x/y); if y>0 then fi:=pi/2-f else fi:=-pi/2-f end end;
Проблема с приведением типов на Паскале
Начинающие «паскалисты» нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие «баги». Вот простейший пример.
var a,b:integer;
r:longint;
begin
a:=1000;
b:=200;
r:=a*b;
writeln (r);
end. Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer, а потом «испорченный» результат переписали в переменную типа Longint. ничего не изменит и
r:=Longint(a*b);
Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint. А вот
r:=Longint(a)*b;
рулит, получите свои 200000 
Нередко мы сталкиваемся с тем, что нам необходимо возвести число в какую-либо степень. Можно воспользоваться обычным калькулятором. Но это неинтересно и очень часто не подходит под условия поставленной задачи.
Понятие степени в математике
Стоит начать с пояснения математического смысла возведения в степень. Например, нам необходимо возвести некоторое число x в степень y. В математике эта запись выглядела бы так: xy = x ^ y. Это означает, что число x нужно умножить на себя y раз. Помните: какое бы вы число ни возводили в нулевую степень, получится единица, а также при возведении в первую степень мы получим наше исходное число. При возведении в отрицательную степень мы всего лишь переворачиваем полученный результат.
Возведение в степень на паскале
С математикой всё понятно. Но как же нам сделать такую программу, которая будет производить возведение в степень? Тут всё просто. Если нам необходимо возвести x в степень 5, то наш код примет вид: res:= x * x * x * x * x. Мы умножили число x на себя 5 раз, как нам и было необходимо, но что делать, если нам не известна степень, в которую необходимо возвести число? Далее мы рассмотрим, как производить возведение в степень. Паскаль предоставляет нам не очень много возможностей для этого, но мы обязательно что-нибудь придумаем. Например, использование стандартных функций и процедур или использование различных циклов.
Возведение числа в квадрат
Начнём, пожалуй, с возведения в квадрат. Возведение в квадрат является частным случаем возведения в степень. Для этого в паскале предусмотрена стандартная процедура sqr(x). Она возведёт наше число x в квадрат, эта запись равна записи x*x.
Очень часто этого вполне достаточно, но не всегда программа может ограничиться одним лишь возведением в квадрат. Как же возводить в более высокие степени? Об этом читаем далее и просвещаемся.
Использование стандартных операторов
В паскале существует два метода для возведения числа в степень: exp(ln(x)*y) и метод power(x, y). Процедура exp() имеет ограничение: x должно быть больше 0, т.к. нельзя извлечь натуральный логарифм из неположительного числа, но эта функция считается устаревшей и неудобной для использования, поэтому дальше мы о ней говорить не будем. Функция power() принимает два значения, первое число (x) — которое нужно возвести в степень, второе число (y) — степень, в которую нужно возвести и возвращает x в степени y. Следует помнить, что числа х и у — вещественные, то есть типа real.
Но тут есть один недостаток, эта функция есть не во всех версиях паскаля. Да и вообще, иногда возведение в степень должно производиться без использования операторов. Идём дальше и разбираем следующий способ.
Возведение в степень при помощи цикла for
Как мы уже поняли, возведение числа в степень — это последовательное умножение числа на само себя несколько раз. Повторить какое-то действие несколько раз в программировании гораздо легче, чем в жизни. Воспользуемся циклом for:
Разберемся, что и как тут работает. Для начала мы вводим два числа: x и y. Затем берём за результат единицу, для чего это — ниже. Выполняем цикл до модуля нашей степени, т.к. если степень будет отрицательной, то цикл не пойдёт. В цикле мы умножаем наш результат на само число x. Так зачем мы присваивали результату 1? Во-первых, если бы мы умножали на 0, то программа всегда выдавала бы 0. Во-вторых, наша степень может быть равна 0, тогда программа должна вернуть нам 1, т.к. любое число в 0 степени это 1. Затем мы проверяем, является степень отрицательным числом или положительным: если она отрицательна, то делим единицу на наш результат. Выполнение этой задачи при помощи цикла while делается почти так же.
Использование цикла while при возведении в степень
Использование цикла while более правильно, нежели for, но для понимания проще предыдущий вариант. Вряд ли можно стоит ограничиваться одним лишь циклом for, для понимания будет лучше посмотреть несколько примеров, да и задача бывает поставлена по-разному, кому-то одним циклом, кому-то другим, именно поэтому мы разберём ещё один способ возведения в степень.
Всё почти так же, как и раньше. Вводим два числа х и у. Присваиваем нашему результату значение единицы, чтобы возводить в нулевую степень. Затем создаём счётчик i и присваиваем ему значение модуля нашей степени. Цикл идёт до тех пор, пока счётчик не равен нулю, если степень с самого начала равна нулю, то цикл не будет выполняться, результат так и останется единицей, как и должно быть, ведь любое число в нулевой степени — это единица. В самом цикле мы всё так же считаем результат, умножая уже полученный результат на наше число х, не забываем вычитать из нашего счётчика единицу, иначе мы никогда не дойдём до нуля. Ну а затем так же, как выше, преобразование, если степень была отрицательной. Ничего сложного, как оказалось. Впрочем, никто и не сомневался.
Что же, с обычными числами мы закончили, но ведь есть не только такие числа.
Понятие комплексных чисел
Нам с самого начала школьного обучения объясняют только обычные числа, но есть ведь ещё и другие, например, комплексные числа. Они довольно сложны в представлении, особенно учитывая то, что нас почти нигде не знакомят с ними. В математической записи они имеют вид z = x + yi, где x и y — это некоторые числа, а i — мысленная единица. Вы сразу подумали: да это же обычное число, стоит просто провести операцию сложения. Но нет, не всё так просто. Это не сумма, это именно число. Другими словами, если попытаться представить это всё с точки зрения геометрии, то можно заменить знак сложения точкой с запятой, и получатся как бы координаты точки, x и y. И если построить нулевой вектор до этой точки, то мы сможем визуально увидеть всё это. Кажется, текста стало слишком много, давайте немного посмотрим:
Если мы хотим показать, что наша плоскость комплексная, достаточно пометить её жирной буквой C, как тут. Затем мы можем видеть множество точек, давайте посмотрим на них и попытаемся понять, какая из них как записывается. Берём точку z1, опускаем проекцию на ось ReZ и получаем 3, затем на ось lmZ и получаем 1,75, в итоге имеем число z1=3 + 1.75i. Вроде всё понятно, давайте ещё раз, для закрепления. Точка z2, по горизонтальной оси — два, по вертикальной — четыре, в итоге имеем: z2=2 + 4i. Всё предельно понятно и просто.
С комплексными числами возможны все те же операции, что и с обычными. Сложение, вычитание, умножение, деление. Но в этой статье мы подробно остановимся на возведении комплексного числа в степень.
Возведение в степень комплексного числа
Что делать, если нужно возвести в степень комплексное число? Не паникуйте! Всё точно так же, как с обычными числами, но чуточку сложнее. Начнём с квадрата. Дано число z = 2 + 5i. Возводим в квадрат, получаем z2 = (2 + 5i)2 = (2 + 5i)(2 + 5i) — а это обычный двучлен, можно просто перемножить, привести подобные слагаемые и всё. Это очень просто, но что делать, когда нужно возвести в более высокую степень? Для начала следует представить наше число в тригонометрической форме, например:
Затем необходимо воспользоваться формулой возведения комплексных чисел в тригонометрической форме: zn=|z|n * (cos(nx) + i * sin(nx)). Можно заметить, что при возведении комплексных чисел даже в очень большие степени они сильно не изменяются, так что не пугайтесь, это сложно, но с практикой всё придёт.
Таким образом, теперь вы знаете, как возводить числа в степень в математике, на языке программирования паскаль, также узнали, что такое комплексные числа и как их возводить в степень. Всё оказалось куда проще, чем вы думали. Не так ли? Остаётся лишь попробовать всё на своём опыте, и всё встанет на свои места. Любая задача, связанная с возведением в степень, теперь решается очень легко для вас.
Модератор: Модераторы
Re: Как в FreePascal возвести число в степень?
modestusmunh » 16.10.2011 09:11:50
Нет результата.
Ошибка в строке, где используются Экспонента и Логарифм натуральный.
- Код: Выделить всё
fZi:=EXP(3*LN(Zi))-SQR(Zi)*((b*P)/(R*T)+1)+(Zi*a*P)/(SQR(R)*SQR(T))-(a*b*SQR(P))/(EXP(3*LN(R))*EXP(3*LN(T)));
Как быть, не знаю. Пришлось заменять на Zi*Zi*Zi и т.д.
- modestusmunh
- новенький
- Сообщения: 13
- Зарегистрирован: 07.09.2011 16:51:00
Re: Как в FreePascal возвести число в степень?
sign » 16.10.2011 09:56:40
У меня всё без ошибок прошло.
- Код: Выделить всё
var fZi, Zi, b, P, R, T, l, k, a: Extended;
begin
Zi := 3; b := 3; P := 3; R := 3; T := 3; a := 3;
fZi:=EXP(3*LN(Zi))-SQR(Zi)*((b*P)/(R*T)+1)+(Zi*a*P)/(SQR(R)*SQR(T))-(a*b*SQR(P))/(EXP(3*LN(R))*EXP(3*LN(T)));
Результат: 9.2222222222222214
- sign
- энтузиаст
- Сообщения: 1131
- Зарегистрирован: 30.08.2009 09:20:53
- Odyssey
- энтузиаст
- Сообщения: 581
- Зарегистрирован: 29.11.2007 17:32:24
Re: Как в FreePascal возвести число в степень?
VSL » 22.04.2012 18:09:32
Похоже это не совсем то что нужно.
-5 в квадрат возводит правильно, а вот 5 в минус вторую степень не хочет, выдает ноль.
Специально искал такую тему. Очень нужен алгоритм возведения в степень для подпрограммы. Алгоритм должен быть универсальным, работать с дробными числами любого знака. Есть такой?
Я сам вот такой алгоритм накидал, подскажите, есть в нем ошибки?
- Код: Выделить всё
function stp(Osnovan,Stpn:real):real; //Подпрограмма вычисления степени
var pow:real;
begin
if (Stpn=0) then pow:=1 else
if (Osnovan > 0) then pow:= Exp(Stpn*Ln(Abs(Osnovan))) else
if (Osnovan < 0) then pow:= (-1)*Exp(Stpn*Ln(Abs(Osnovan))) else
if (Osnovan=0) then pow:=0;
stp:=pow;
end;
- VSL
- новенький
- Сообщения: 11
- Зарегистрирован: 22.04.2012 15:14:39
Re: Как в FreePascal возвести число в степень?
VSL » 23.04.2012 16:36:50
kosteek писал(а):А можно ли содрать ф-цию power из модуля math?
Попробовал. В целом все работает, но не возводит отрицательное число в дробную степень. Нужен универсальный алгоритм.
- VSL
- новенький
- Сообщения: 11
- Зарегистрирован: 22.04.2012 15:14:39
Re: Как в FreePascal возвести число в степень?
Little_Roo » 23.04.2012 18:37:35
VSL писал(а): В целом все работает, но не возводит отрицательное число в дробную степень.
А разве подкоренное (число в дробной степени) выражение не должно быть НЕОТРИЦАТЕЛЬНЫМ ?????
Курим ОДЗ
-
Little_Roo - энтузиаст
- Сообщения: 632
- Зарегистрирован: 27.02.2009 19:56:36
- Откуда: Санкт-Петербург
Re: Как в FreePascal возвести число в степень?
daesher » 23.04.2012 22:25:52
Little_Roo писал(а):А разве подкоренное (число в дробной степени) выражение не должно быть НЕОТРИЦАТЕЛЬНЫМ ?????
Курим ОДЗ
Не совсем. Например, корень нечётной степени будет действительным для любого действительного аргумента. С отрицательным аргументом стандартная функция power не работает.
- daesher
- постоялец
- Сообщения: 224
- Зарегистрирован: 09.03.2010 22:17:14
Re: Как в FreePascal возвести число в степень?
absdjfh » 13.03.2013 22:19:03
Хоть тема и старая, но все же важно замечание.
daesher писал(а):Не совсем. Например, корень нечётной степени будет действительным для любого действительного аргумента. С отрицательным аргументом стандартная функция power не работает.
Вы не правы, хотя в этом рассуждении есть логика (которую я хотел бы поддерживать). Но любой учебник математики говорит, что
Выражения (-2)^(1/3), (-243)^(3/5), (-16)^(2/3) не имеют смысла, так как по определению основание степени с рациональным показателем может быть только неотрицательным.
- absdjfh
- новенький
- Сообщения: 60
- Зарегистрирован: 21.01.2012 13:59:00
Re: Как в FreePascal возвести число в степень?
sv503 » 04.07.2013 12:51:00
absdjfh писал(а):Выражения (-2)^(1/3), (-243)^(3/5), (-16)^(2/3) не имеют смысла, так как по определению основание степени с рациональным показателем может быть только неотрицательным.
В математике мало какие вычислительные операции не имеют смысла. Результатами приведённых выражений будут комплексные числа.
- sv503
- незнакомец
- Сообщения: 1
- Зарегистрирован: 04.07.2013 11:58:59
Re: Как в FreePascal возвести число в степень?
SSerge » 05.07.2013 05:38:34
sv503 писал(а):Результатами приведённых выражений будут комплексные числа.
Провокационный вопрос: к какому типу переменной соотносятся комплексные числа?
Если задуматься над этим аспектом, то у вас все вычисления с такими числами должны быть в математике, которая работает с комплексными числами, а тут проблема не только с возведением в степень
- SSerge
- энтузиаст
- Сообщения: 927
- Зарегистрирован: 12.01.2012 05:34:14
- Откуда: Барнаул
Re: Как в FreePascal возвести число в степень?
Undernooob » 27.09.2016 19:12:41
Не так давно начал изучать fpc и столкнулся с проблемой возведения в степень, а именно x^(0.1x) при том что x принимает значения от — 10 до -2 и значения типа real, например, число -9.6 в калькуляторе возводится в степень -0.96, а -7.8 в степень -0.78 — нет, и так же надо бы в паскале чтоб возводило
- Undernooob
- незнакомец
- Сообщения: 1
- Зарегистрирован: 27.09.2016 19:01:39
Вернуться в Алгоритмы
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1
| В своей жизни писал проги на Pascal’e два или три раза. Тут пришлось лабы на нем писать и у меня возник такой вопрос, как на Паскале возводить в произвольную степень? Ну типа есть что-то в роде функции pow? | |
| Power, только вроде надо math подключить… | |
| Аналога функции pow там нет. begin для степени с вещ. показателем, запамятовал, там вроде формула была.(из вышмата) | |
| 2Death Moroz: медленно будет работать — слишком много операций… | |
| 2JUmPER ты в универовских лабах оптимизацию когданибудь делал ? | |
| uses math; begin | |
| Death Moroz Guest | Это нравится:0Да/0Нет 11.09.2005 21:26:06
Эт ты из какого паскаля нарезал? | ||
| ksor Guest | Это нравится:0Да/0Нет 11.09.2005 23:21:12 можно еще так :
без всяких доп. модулей… | ||
| когда я учился( а это было лет 15 назад) за такое возведение в степень ( степень была с целым показателем) меня чуть преп не расстрелял:)) | |
| Угу, там нет возведения в степень. Выбирай любой способ в зависимости от цели. | |
| Интересно, что быстрее работает — тупое перемножение в цикле, или вариант с экспонентой? Имхо, второе быстрее во всех случаях | |
| Если нужна скорость, то лучше всего использовать рекурсивный алгоритм: pow(a,n) { n — целое число. | |
| Death Moroz Guest | Это нравится:0Да/0Нет 14.09.2005 04:26:48
Ты в паскале оператор return видел??)) | ||
| Строго говоря, это и не Си. Это абстрактное описание алгоритма. | |
| Всем большое спасибо за ответы, проканал прикол с экспонентой. | |
| Death Moroz Guest | Это нравится:0Да/0Нет 15.09.2005 17:42:49
Просто Николасу Вирту было влом ввести оператор возаедения в степень, он типа подумал — сами делайте. | ||
| Phoenix Guest | Это нравится:0Да/0Нет 15.09.2005 18:28:46
во первых рекурсивный алгоритм скорости не приьбавт, иьбо это етсь тот же цикл. | ||
| moonspell Guest | Это нравится:0Да/0Нет 15.09.2005 20:57:50
По-моему, ты прежде чем ответить даже не удосужился на описание алгоритма посмотреть. Это НЕ | ||
| X_Tra Guest | Это нравится:0Да/0Нет 16.09.2005 14:00:28 В Дельфях в модуле math функция IntPower написана на асме (+ закомментаренная реализация циклом). А функция Power как раз через экспоненту и сделана:
| ||
| Phoenix Guest | Это нравится:0Да/0Нет 17.09.2005 20:31:16
виноват признаю… | |||
Раздел: Стандартные функции Паскаля
Функция Power в Паскале (и многих других языках программирования) выполняет возведение числа в степень.
Синтаксис для вещественных чисел:
function Power(Base: Double; Expon: Double) : Double;
Синтаксис для целых чисел:
function Power(Base: LongInt; Expon: LongInt) : LongInt;
Эта функция возводит число Base в степень Expon и возвращает результат. В реальности функция возвращает результат выражения:
Exp(Expon * Ln(Base))
ВАЖНО!
Всё, что сказано выше, взято из официальной документации
FreePascal. Однако документация иногда расходится с действительностью. Во всяком случае, мой компилятор не соответствует документации. А именно:
- В документации сказано, что функция объявлена в модуле SYSTEM. Однако без подключения модуля MATH компилятор выдаёт ошибку. Из этого следует, что на самом деле функция объявлена в модуле MATH.
- В документации приведён синтаксис как для целых, так и для вещественных чисел. Однако на самом деле функция работает только с вещественными числами. При попытке использовать целые числа компилятор также выдаёт ошибку.
- Возможно, в более новых версиях эти проблемы уже исправлены. Но у меня было именно так (версия FPC 3.0.0).
Пример использования функции Power
Пример приведён ниже:
program funcpower; uses Math; var x, y, z : single; begin x := 2; y := 3; z := Power(x, y); //Z = X в степени Y WriteLn(z:0:2); ReadLn; end.
Здесь мы число 2 (переменная Х) возводим в степень 3 (переменная Y), то есть вычисляем следующую формулу:
Z = XY
Обратите внимание на подключенный модуль MATH.
Эта статья входит в раздел о подпрограммах модуля SYSTEM. И по идее описания функции Power здесь не должно быть. Но, так как в документации сказано, что функция Power объявлена в модуле SYSTEM, я решил включить данную статью именно в этот раздел (я же не виноват, что в документации косяк))).
Возведение в степень в Паскале
Возведение в степень в Паскале можно выполнить и без какой-то специальной функции,
используя функцию вычисления натурального логарифма
и функцию вычисления экспоненты.
О том, как это сделать, я рассказал здесь.
Однако, если есть специальная функция для возведения числа в степень, то почему бы ей и не воспользоваться? С одной стороны. С другой стороны — эта функция совершенно неожиданно требует подключения модуля MATH.
В документации сказано, что по сути функция Power работает по формуле возведения в степень в Паскале:
Exp(Expon * Ln(Base))
Однако, если мы будем делать именно так, эта формула будет неправильно работать с
отрицательными числами, потому что в документации сказано, что функция Ln работает только с положительными числами.
Так что функция Power в реальности несколько сложнее, чем приведённая выше формула.
Поэтому для разминки мы напишем свой аналог функции Power, который будет работать правильно. Но для начала вспомним как вычисляется степень числа:
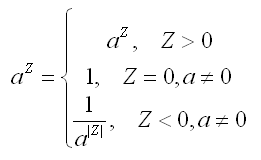
Также напомню, что любое число в нулевой степени равно 1, а ноль в любой степени равен 0 (кроме нуля в нулевой — ноль в нулевой степени не определён, но мы будем возвращать в таких случаях ноль, хотя функция Power возвращает 1).
А теперь наш аналог функции Power:
function AVPower(Base: Double; Expon: Double) : Double;
var m : byte;
i : integer;
Res : Double;
begin
m := 0;
if Expon
Я сознательно немного всё усложнил, чтобы вас запутать )))
Пример использования функций Power и её аналога в программе:
x := 2; y := 3; z := Power(x, y); //Z = X в степени Y WriteLn(z:0:2); z := AVPower(x, y); //Z = X в степени Y WriteLn(z:0:2);
Здесь есть один подвох — если вы попытаетесь возвести отрицательное число в не целую степень, например, так:
-23,5
то стандартная функция Power вызовет ошибку во время выполнения программы. В своём аналоге я этого избежал, но надо понимать, что результат в этом случае будет неправильным (хотя с моей точки зрения это всё-равно лучше, чем аварийное завершение программы).
Это происходит потому, что при таком раскладе результатом являются комплексные числа, а операции с комплексными числами выполняются по другим правилам.
В реальных программах подобные ситуации надо дополнительно обрабатывать (хотя бы предупреждать пользователя о том, что при отрицательном основании и не целой степени функция вернёт неправильный результат).
Ещё в моей функции используется функция Odd, о которой я ещё не рассказывал. Вкратце скажу, что она определяет, является ли число чётным. Более подробно о ней расскажу в отдельной статье.
| | Как стать программистом 2.0 Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… |