Среднеарифметическое значение как пишется

Содержание

Общие сведения
Смешанные числа
Алгоритм нахождения среднего значения
Пример решения

Общие сведения

Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:

Целые.

Дробные.

Первый тип — натуральные числа, они применяются при устном счете предметов.

Дробные бывают также двух типов:

Десятичными.

Обыкновенными.

Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.

В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.

Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.

Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.

Смешанные числа

Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:

Записать неправильную дробь: 79/11.

Рассчитать целое число: 79/11=7.

Вычислить новое значение числителя: 79−11*7=2.

Записать смешанную величину: 7 2/11.

Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:

Записать смешанное выражение: 7[2/11].

Вычислить величину нового числителя: 7*11+2=79.

Результат: 79/11.

Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.

Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.

Алгоритм нахождения среднего значения

Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.

Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.

Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.

Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.

Методика определения среднеарифметического значения:

Записать все значения.

Сложить все элементы, записанные в первом пункте.

Поделить сумму, полученную на втором шаге, на количество элементов.

Записать результат.

Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:

Количество элементов: 5.

Сумма: 4+7+8+12+15=46.

Среднее арифметическое: 46/5=9,2.

Результат: 9,2.

В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.

При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.

Пример решения

Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.

Решение выполняется по следующему алгоритму:

Записать величины: 3 2/3, 4 5/7 и 6 3/8.

Количество: 3.

Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.

Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.

Вычислить сумму: 2479/168.

Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.

Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.

Значение искомой величины равно 4 463/504.

При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.

Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.

Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.

Источник: sprint-olympic.ru

Источник

Разбор частей речи

Далее давайте разберем морфологические признаки каждой из частей речи русского языка на примерах. Согласно лингвистике русского языка, выделяют три группы из 10 частей речи, по общим признакам:

1. Самостоятельные части речи:

существительные (см. морфологические нормы сущ. );
глаголы:
- причастия;
- деепричастия;
прилагательные;
числительные;
местоимения;
наречия;

2. Служебные части речи:

предлоги;
союзы;
частицы;

3. Междометия.

Ни в одну из классификаций (по морфологической системе) русского языка не попадают:

слова да и нет, в случае, если они выступают в роли самостоятельного предложения.
вводные слова: итак, кстати, итого, в качестве отдельного предложения, а так же ряд других слов.

Морфологический разбор существительного

План морфологического разбора существительного

Пример:

«Малыш пьет молоко.»

Малыш (отвечает на вопрос кто?) – имя существительное;

начальная форма – малыш;
постоянные морфологические признаки: одушевленное, нарицательное, конкретное, мужского рода, I -го склонения;
непостоянные морфологические признаки: именительный падеж, единственное число;
при синтаксическом разборе предложения выполняет роль подлежащего.

Морфологический разбор слова «молоко» (отвечает на вопрос кого? Что?).

начальная форма – молоко;
постоянная морфологическая характеристика слова: среднего рода, неодушевленное, вещественное, нарицательное, II -е склонение;
изменяемые признаки морфологические: винительный падеж, единственное число;
в предложении прямое дополнение.

Приводим ещё один образец, как сделать морфологический разбор существительного, на основе литературного источника:

«Две дамы подбежали к Лужину и помогли ему встать. Он ладонью стал сбивать пыль с пальто. (пример из: «Защита Лужина», Владимир Набоков).»

Дамы (кто?) — имя существительное;

начальная форма — дама;
постоянные морфологические признаки: нарицательное, одушевленное, конкретное, женского рода, I склонения;
непостоянная морфологическая характеристика существительного: единственное число, родительный падеж;
синтаксическая роль: часть подлежащего.

Лужину (кому?) — имя существительное;

начальная форма — Лужин;
верная морфологическая характеристика слова: имя собственное, одушевленное, конкретное, мужского рода, смешанного склонения;
непостоянные морфологические признаки существительного: единственное число, дательного падежа;
синтаксическая роль: дополнение.

Ладонью (чем?) — имя существительное;

начальная форма — ладонь;
постоянные морфологические признаки: женского рода, неодушевлённое, нарицательное, конкретное, I склонения;
непостоянные морфо. признаки: единственного числа, творительного падежа;
синтаксическая роль в контексте: дополнение.

Пыль (что?) — имя существительное;

начальная форма — пыль;
основные морфологические признаки: нарицательное, вещественное, женского рода, единственного числа, одушевленное не охарактеризовано, III склонения (существительное с нулевым окончанием);
непостоянная морфологическая характеристика слова: винительный падеж;
синтаксическая роль: дополнение.

(с) Пальто (С чего?) — существительное;

начальная форма — пальто;
постоянная правильная морфологическая характеристика слова: неодушевленное, нарицательное, конкретное, среднего рода, несклоняемое;
морфологические признаки непостоянные: число по контексту невозможно определить, родительного падежа;
синтаксическая роль как члена предложения: дополнение.

Морфологический разбор прилагательного

Имя прилагательное — это знаменательная часть речи. Отвечает на вопросы Какой? Какое? Какая? Какие? и характеризует признаки или качества предмета. Таблица морфологических признаков имени прилагательного:

начальная форма в именительном падеже, единственного числа, мужского рода;
постоянные морфологические признаки прилагательных:
- разряд, согласно значению:
- - — качественное (теплый, молчаливый);
  - — относительное (вчерашний, читальный);
  - — притяжательное (заячий, мамин);
- степень сравнения (для качественных, у которых этот признак постоянный);
- полная / краткая форма (для качественных, у которых этот признак постоянный);
непостоянные морфологические признаки прилагательного:
- качественные прилагательные изменяются по степени сравнения (в сравнительных степенях простая форма, в превосходных — сложная): красивый-красивее-самый красивый;
- полная или краткая форма (только качественные прилагательные);
- признак рода (только в единственном числе);
- число (согласуется с существительным);
- падеж (согласуется с существительным);
синтаксическая роль в предложении: имя прилагательное бывает определением или частью составного именного сказуемого.

План морфологического разбора прилагательного

Пример предложения:

Полная луна взошла над городом.

Полная (какая?) – имя прилагательное;

начальная форма – полный;
постоянные морфологические признаки имени прилагательного: качественное, полная форма;
непостоянная морфологическая характеристика: в положительной (нулевой) степени сравнения, женский род (согласуется с существительным), именительный падеж;
по синтаксическому анализу — второстепенный член предложения, выполняет роль определения.

Вот еще целый литературный отрывок и морфологический разбор имени прилагательного, на примерах:

Девушка была прекрасна: стройная, тоненькая, глаза голубые, как два изумительных сапфира, так и заглядывали к вам в душу.

Прекрасна (какова?) — имя прилагательное;

начальная форма — прекрасен (в данном значении);
постоянные морфологические нормы: качественное, краткое;
непостоянные признаки: положительная степень сравнения, единственного числа, женского рода;
синтаксическая роль: часть сказуемого.

Стройная (какая?) — имя прилагательное;

начальная форма — стройный;
постоянные морфологические признаки: качественное, полное;
непостоянная морфологическая характеристика слова: полное, положительная степень сравнения, единственное число, женский род, именительный падеж;
синтаксическая роль в предложении: часть сказуемого.

Тоненькая (какая?) — имя прилагательное;

начальная форма — тоненький;
морфологические постоянные признаки: качественное, полное;
непостоянная морфологическая характеристика прилагательного: положительная степень сравнения, единственное число, женского рода, именительного падежа;
синтаксическая роль: часть сказуемого.

Голубые (какие?) — имя прилагательное;

начальная форма — голубой;
таблица постоянных морфологических признаков имени прилагательного: качественное;
непостоянные морфологические характеристики: полное, положительная степень сравнения, множественное число, именительного падежа;
синтаксическая роль: определение.

Изумительных (каких?) — имя прилагательное;

начальная форма — изумительный;
постоянные признаки по морфологии: относительное, выразительное;
непостоянные морфологические признаки: множественное число, родительного падежа;
синтаксическая роль в предложении: часть обстоятельства.

Морфологические признаки глагола

Согласно морфологии русского языка, глагол — это самостоятельная часть речи. Он может обозначать действие (гулять), свойство (хромать), отношение (равняться), состояние (радоваться), признак (белеться, красоваться) предмета. Глаголы отвечают на вопрос что делать? что сделать? что делает? что делал? или что будет делать? Разным группам глагольных словоформ присущи неоднородные морфологические характеристики и грамматические признаки.

Морфологические формы глаголов:

начальная форма глагола — инфинитив. Ее так же называют неопределенная или неизменяемая форма глагола. Непостоянные морфологические признаки отсутствуют;
спрягаемые (личные и безличные) формы;
неспрягаемые формы: причастные и деепричастные.

Морфологический разбор глагола

начальная форма — инфинитив;
постоянные морфологические признаки глагола:
- переходность:
- - переходный (употребляется с существительными винительного падежа без предлога);
  - непереходный (не употребляется с существительным в винительном падеже без предлога);
- возвратность:
- - возвратные (есть -ся, -сь);
  - невозвратные (нет -ся, -сь);
- вид:
- - несовершенный (что делать?);
  - совершенный (что сделать?);
- спряжение:
- - I спряжение (дела-ешь, дела-ет, дела-ем, дела-ете, дела-ют/ут);
  - II спряжение (сто-ишь, сто-ит, сто-им, сто-ите, сто-ят/ат);
  - разноспрягаемые глаголы (хотеть, бежать);
непостоянные морфологические признаки глагола:
- наклонение:
- - изъявительное: что делал? что сделал? что делает? что сделает?;
  - условное: что делал бы? что сделал бы?;
  - повелительное: делай!;
- время (в изъявительном наклонении: прошедшее/настоящее/будущее);
- лицо (в настоящем/будущем времени, изъявительного и повелительного наклонения: 1 лицо: я/мы, 2 лицо: ты/вы, 3 лицо: он/они);
- род (в прошедшем времени, единственного числа, изъявительного и условного наклонения);
- число;
синтаксическая роль в предложении. Инфинитив может быть любым членом предложения:
- сказуемым: Быть сегодня празднику;
- подлежащим :Учиться всегда пригодится;
- дополнением: Все гости просили ее станцевать;
- определением: У него возникло непреодолимое желание поесть;
- обстоятельством: Я вышел пройтись.

Морфологический разбор глагола пример

Чтобы понять схему, проведем письменный разбор морфологии глагола на примере предложения:

Вороне как-то Бог послал кусочек сыру… (басня, И. Крылов)

Послал (что сделал?) — часть речи глагол;

начальная форма — послать;
постоянные морфологические признаки: совершенный вид, переходный, 1-е спряжение;
непостоянная морфологическая характеристика глагола: изъявительное наклонение, прошедшего времени, мужского рода, единственного числа;
синтаксическая роль в предложении: сказуемое.

Следующий онлайн образец морфологического разбора глагола в предложении:

Какая тишина, прислушайтесь.

Прислушайтесь (что сделайте?) — глагол;

начальная форма — прислушаться;
морфологические постоянные признаки: совершенный вид, непереходный, возвратный, 1-го спряжения;
непостоянная морфологическая характеристика слова: повелительное наклонение, множественное число, 2-е лицо;
синтаксическая роль в предложении: сказуемое.

План морфологического разбора глагола онлайн бесплатно, на основе примера из целого абзаца:

— Его нужно предостеречь.

— Не надо, пусть знает в другой раз, как нарушать правила.

— Что за правила?

— Подождите, потом скажу. Вошел! («Золотой телёнок», И. Ильф)

Предостеречь (что сделать?) — глагол;

начальная форма — предостеречь;
морфологические признаки глагола постоянные: совершенный вид, переходный, невозвратный, 1-го спряжения;
непостоянная морфология части речи: инфинитив;
синтаксическая функция в предложении: составная часть сказуемого.

Пусть знает (что делает?) — часть речи глагол;

начальная форма — знать;
постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
непостоянная морфология глагола: повелительное наклонение, единственного числа, 3-е лицо;
синтаксическая роль в предложении: сказуемое.

Нарушать (что делать?) — слово глагол;

начальная форма — нарушать;
постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
непостоянные признаки глагола: инфинитив (начальная форма);
синтаксическая роль в контексте: часть сказуемого.

Подождите (что сделайте?) — часть речи глагол;

начальная форма — подождать;
постоянные морфологические признаки: совершенный вид, невозвратный, переходный, 1-го спряжения;
непостоянная морфологическая характеристика глагола: повелительное наклонение, множественного числа, 2-го лица;
синтаксическая роль в предложении: сказуемое.

Вошел (что сделал?) — глагол;

начальная форма — войти;
постоянные морфологические признаки: совершенный вид, невозвратный, непереходный, 1-го спряжения;
непостоянная морфологическая характеристика глагола: прошедшее время, изъявительное наклонение, единственного числа, мужского рода;
синтаксическая роль в предложении: сказуемое.

Источник

Общие сведения

Целые.
Дробные.

Первый тип — натуральные числа, они применяются при устном счете предметов.

Дробные бывают также двух типов:

Десятичными.
Обыкновенными.

Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.

Смешанные числа

Записать неправильную дробь: 79/11.
Рассчитать целое число: 79/11=7.
Вычислить новое значение числителя: 79−11*7=2.
Записать смешанную величину: 7 2/11.

Записать смешанное выражение: 7[2/11].
Вычислить величину нового числителя: 7*11+2=79.
Результат: 79/11.

Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.

Алгоритм нахождения среднего значения

Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.

Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.

Методика определения среднеарифметического значения:

Записать все значения.
Сложить все элементы, записанные в первом пункте.
Поделить сумму, полученную на втором шаге, на количество элементов.
Записать результат.

Количество элементов: 5.
Сумма: 4+7+8+12+15=46.
Среднее арифметическое: 46/5=9,2.
Результат: 9,2.

При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.

Пример решения

Решение выполняется по следующему алгоритму:

Записать величины: 3 2/3, 4 5/7 и 6 3/8.
Количество: 3.
Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.
Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.
Вычислить сумму: 2479/168.
Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.
Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.
Значение искомой величины равно 4 463/504.

Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.

Источник

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

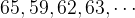
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Два наблюдения:

Среднее арифметическое находится посередине двух чисел (больше меньшего, но меньше большего).
Среднее арифметическое не всегда входит в анализируемый набор чисел (не равно ни одному из двух чисел).

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

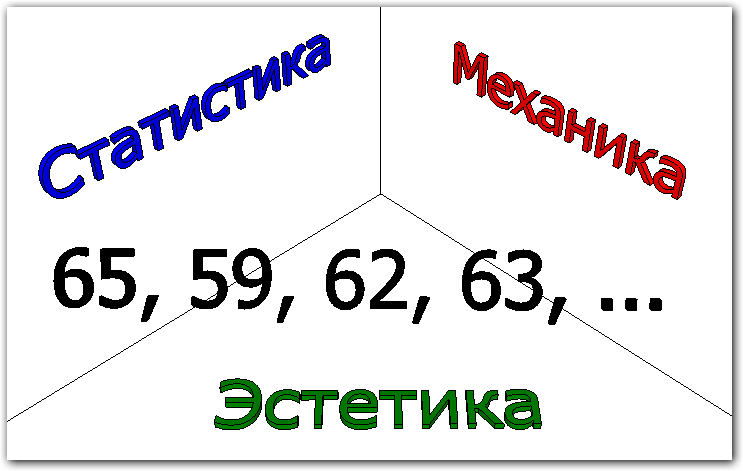
В механике момент силы – это произведение силы F на расстояние l:

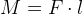
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

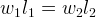
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

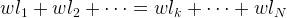
Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

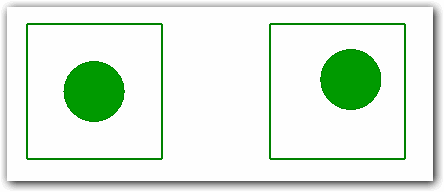
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

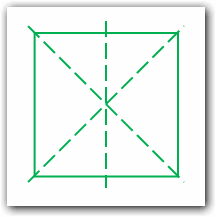
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

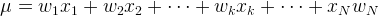
Это и есть формула математического ожидания.

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

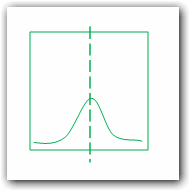
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

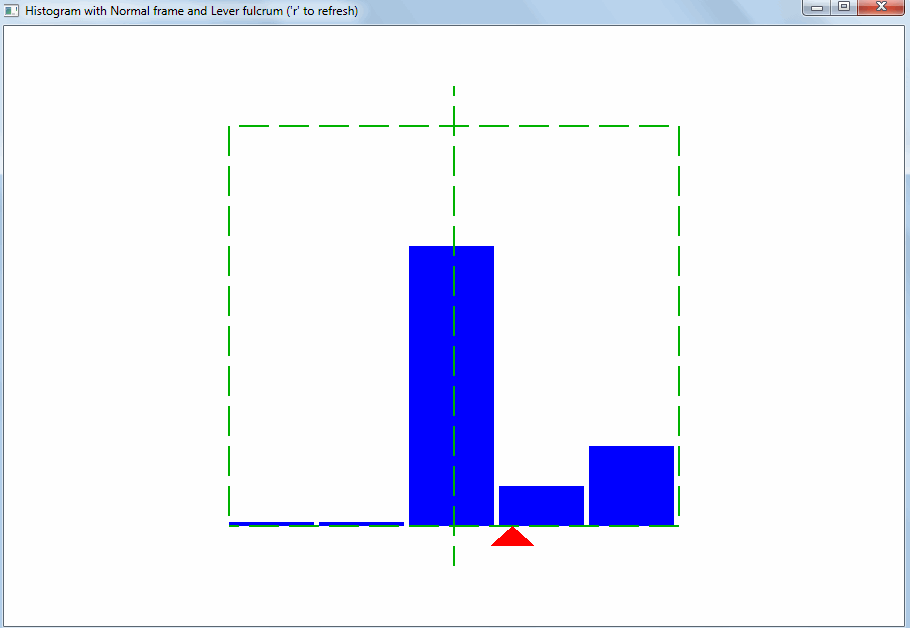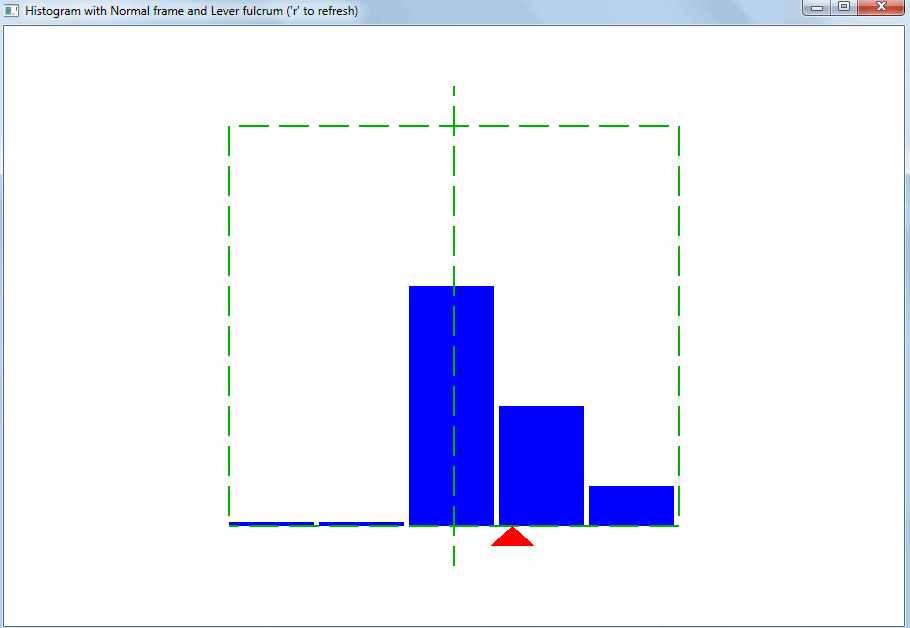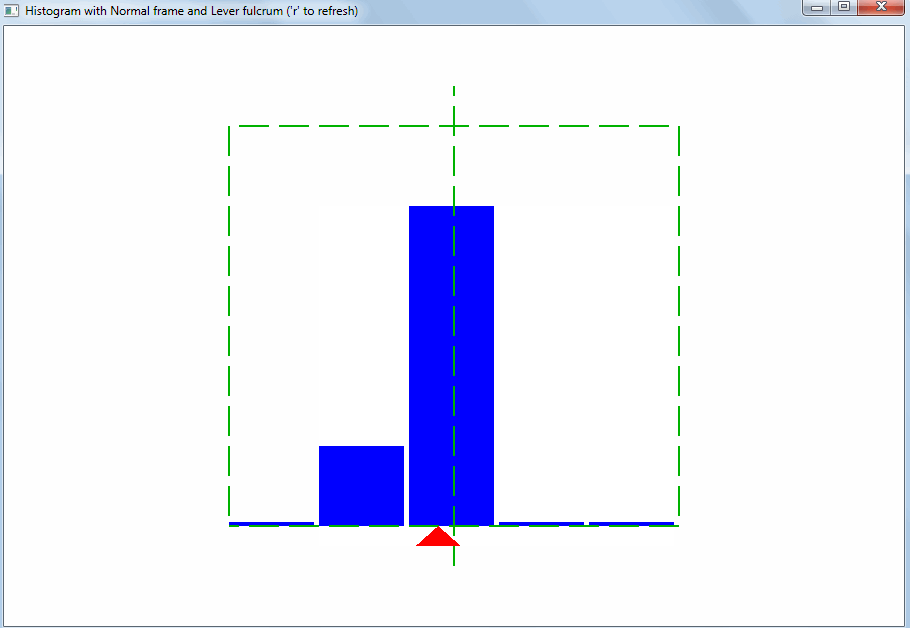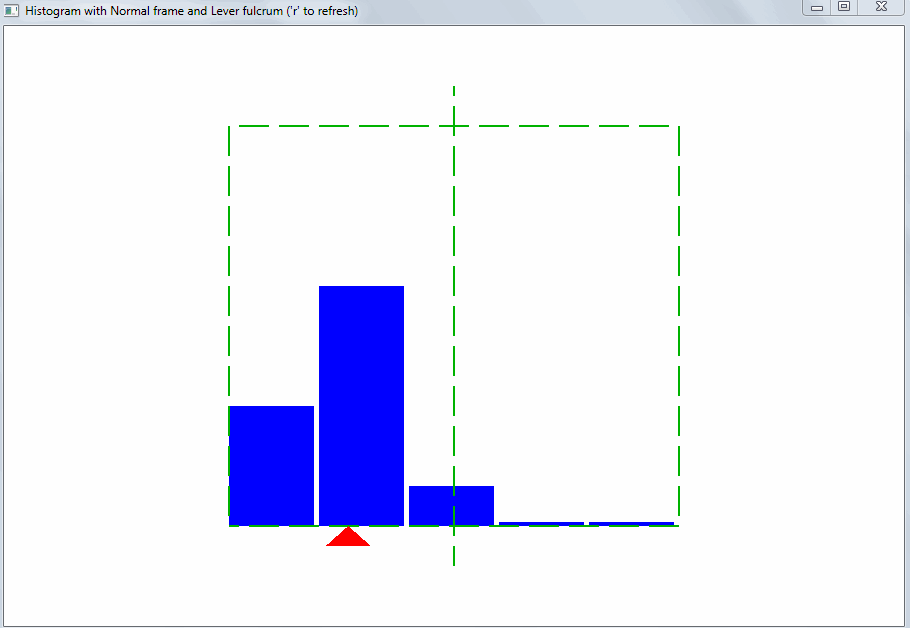
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Среднее арифметическое – интегральная характеристика набора числовых данных (выборки). Применяется как описательная характеристика в совокупности с другими.
Нормально, что среднее значение не входит в набор данных. Среднее арифметическое не может заменить полное описание полученной выборки.
Интервал значений гистограммы должен быть подобран таким образом, чтобы ожидаемое среднее арифметическое было посередине. Тогда будет сразу видно отклонение параметров выборки от ожидаемых значений.
Среднее арифметическое подвержено влиянию выбросов – значений, сильно отличающихся от остальных значений переменной величины.

Ссылки

Wikipedia: Переменная величина, Моменты в статистике и механике, Момент силы, Математическое ожидание
Рудольф Арнхейм. Искусство и визуальное восприятие: фрагменты
Демонстрация гистограммы, ожидаемого среднего и среднего выборки: исходный код для PyOpenGL

Источник

Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.

Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами^[1].

Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).

На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.

Введение

Обозначим множество чисел X = (x₁, x₂, …, x_n) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i из этой совокупности μ = E{x_i} есть математическое ожидание этой выборки.

На практике разница между μ и в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).

Примеры

Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:

Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:

Непрерывная случайная величина

Если существует интеграл от некоторой функции одной переменной, то среднее арифметическое этой функции на отрезке определяется через определённый интеграл:

Здесь для определения отрезка подразумевается, что причём чтобы знаменатель не был равен 0.

Некоторые проблемы применения среднего

Отсутствие робастности

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается около 8,16653826392 % ≈ 8,2 %.

Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35,1. Арифметическое среднее этого роста 10 %, но, поскольку акции выросли за 2 года всего на $5,1, средний рост в 8,2 % даёт конечный результат $35,1:

$30 × (1 – 0,1) (1 + 0,3) = $30 × (1 + 0,082) (1 + 0,082) = $35,1. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: $30 × (1 + 0,1) (1 + 0,1) = $36.3.

Сложный процент в конце 2 года: 90 % * 130 % = 117 %, то есть общий прирост 17 %, а среднегодовой сложный процент , то есть среднегодовой прирост 8,2 %.

Направления

Основная статья: Статистика направлений

При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.

Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).

Примечания

См. также

Арифметическая пропорция
Арифметическая прогрессия
Неравенство Швейцера

Ссылки

Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика

Эта страница в последний раз была отредактирована 6 декабря 2021 в 05:49.

Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

Источник