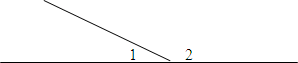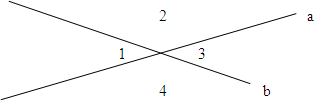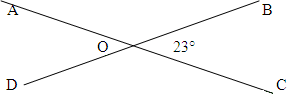Тип урока: урок закрепления нового материала
Цели урока:
- Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
- Развивающие: развивать умение анализировать условие задачи;
- Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).
Структура урока:
- I этап. Организационный момент
- II этап. Актуализация опорных знаний
- III этап. Закрепление изученного материала
- IV этап. Зарядка для глаз
- V этап. Самостоятельная работа
- VI этап. Домашнее задание
- VII этап. Итог урока
Ход урока
I. Организационный момент
(Слайд 1-2)
Приветствие, сообщение темы, целей и задач.
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.
II. Актуализация опорных знаний
(Слайд 3)
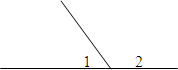
Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)
Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)
Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)
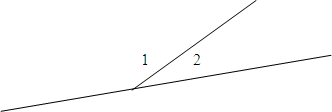
(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?
Ответ.
- Сумма смежных углов равна 180° (теорема)
∠1 + ∠2 = 180°
- Если два угла равны, то и смежные с ними углы равны.
- Если угол не развернутый, то его градусная мера меньше 180°.
- Угол, смежный с прямым, есть прямой угол.
(Слайд 5)
Вопросы. Могут ли два смежных угла быть равными:
а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ: (да, т.к. 83° + 97°= 180°)
(Слайд 6)
Устно.
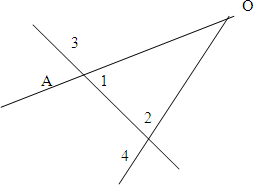
| Дано: ∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4 | Доказательство. 1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, |
| Доказать ∠1 = ∠2 |
(Слайд 7)
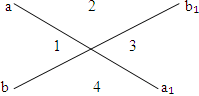
Вопрос. Какие углы называются вертикальными?
(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).
∠ 1 и ∠ 3 – вертикальные углы
∠ 2 и ∠ 4 – вертикальные углы
(Слайд 
Вопрос. Каким свойством обладают смежные углы?
Ответ. Вертикальные углы равны. (теорема)
∠ 1 = ∠ 3
∠ 2 = ∠ 4
III этап. Закрепление изученного материала. Решение задач.
(Слайд 9)
№3 (учебник)
| Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза | Решение. 1. Пусть ∠2 = х, тогда ∠1=2х 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60°, |
| Найти ∠1 и ∠2 |
(Слайд 10)
№6(2)
| Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7 | Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. |
| Найти ∠1 и ∠2 |
(Слайд 11)
| Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1 | Решение 1. Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию). 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° |
| Найти ∠1 и ∠2 |
(Слайд 12)
| Дано: а ∩ b ∠2 меньше ∠1 в 4 раза | Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), Ответ: 144°, 36°, 144°, 36°. |
| Найти ∠1, ∠2, ∠3 и ∠4 |
(Слайд 13)
| Дано: AС ∩ ВD = O ∠ВОС = 23° | Решение 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, 3. ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). Ответ: 157°, 157°, 23°. |
| Найти: ∠СОD, ∠АОВ, ∠АОD. |
(Слайд 14)
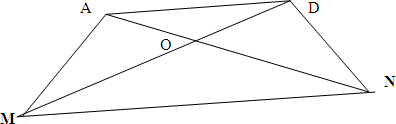
Устно. Вопрос. Назовите смежные и вертикальные углы.
Ответ.
Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .
Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ.
IV этап. Зарядка для глаз
(Слайд 15)
V этап. Самостоятельная работа (на листочках).
| Вариант 1 | Вариант 2 |
| №1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы. | №1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы. |
| №2. Разность смежных углов равна 50°. Найдите меньший угол. | №2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол. |
Ответы
| Вариант 1 | Вариант 2 |
| №1. 93°, 87°, 93°. | №1. 62°, 118°, 62° |
| №2. 75°. | №2. 36°. |
VI этап. Домашнее задание.
- §2. Пункты 14-15.
- Задачи на стр. 26. № 6(4), № 12.
VII этап. Итог урока.
- Повторили понятия смежных и вертикальных углов
- Научились решать задачи, используя знания о смежных и вертикальных углах.
- Стали еще на одну ступеньку выше в изучении геометрии.
Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 8. Самостоятельная работа № 2 «Перпендикулярные прямые» с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 2.
Атанасян 7. Поурочные планы
Самостоятельные работы
Геометрия 7 класс. Урок 8.
Самостоятельная «Перпендикулярные прямые»
I уровень сложности (задания)
II уровень сложности (задания)
III уровень сложности (задания)
Самостоятельная работа № 2
РЕШЕНИЯ и ОТВЕТЫ
I уровень сложности (ответы)
Ответы на Вариант 1 (1-й ур.)
№ 1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы.
ОТВЕТ: Так как ∠1 : ∠2 = 1 : 2, то ∠1 = х, ∠2 = 2х. Но ∠1 + ∠2 = 180°, тогда х + 2х = 180°, x = 60, значит, ∠1 = 60°, ∠2 = 120° (рис. 1.115).
№ 2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.
Указание к решению: Пусть ∠1 = 21°, тогда ∠3 = ∠1 как вертикальные и ∠3 = 21°. ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180° (рис. 1.116). Тогда ∠2 = 180° – ∠1 = 159°. Но ∠2 = ∠4 как вертикальные и ∠4 = 159°.
ОТВЕТ: ∠1 = ∠3 = 21°, ∠2 = ∠4 = 159°.
№ 3. Дано: α = 30°, β = 140° (рис. 1.112). Найти: ∠1, ∠2, ∠3, ∠4.
Указание к решению: α = 30°, тогда ∠4 = 30°, так как ∠4 и угол с градусной мерой α – вертикальные,
β = 140°, тогда ∠2 = 140°, так как ∠2 и угол с градусной мерой β – вертикальные.
∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180° – (∠2 + ∠4) = 10°.
∠3 и ∠1 – вертикальные, поэтому ∠3 = ∠1, ∠1 = 10°.
ОТВЕТ: ∠3 = ∠1 = 10°, ∠2 = 140°, ∠4 = 30°.
Ответы на Вариант 2 (1-й ур.)
№ 1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы.
ОТВЕТ: ∠2 на 20° больше ∠1, тогда ∠1 = х, ∠2 = х + 20° (рис. 1.117). Но ∠1 + ∠2 = 180°, тогда х + х + 20 = 180, x = 80°, значит, ∠1 = 80°, ∠2 = 100°.
№ 2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы.
Указание к решению: Пусть ∠1 = 102°, тогда ∠3 = ∠1 как вертикальные и ∠3 = 102° (рис. 1.118). ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда ∠2 = 180° – ∠1 = 78°. Но ∠2 = ∠4 как вертикальные и ∠4 = 78°.
ОТВЕТ: ∠1 = ∠3 = 102°, ∠2 = ∠4 = 78°.
№ 3. Дано: α = 20°, β = 130° (рис. 1.113). Найти: ∠1, ∠2, ∠3, ∠4.
Указание к решению: α = 20°, тогда ∠4 = 20°, так как ∠4 и угол с градусной мерой α – вертикальные.
β = 130°, тогда ∠2 = 130°, так как ∠2 и угол с градусной мерой β – вертикальные.
∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180° – (∠2 + ∠4) = 30°.
∠3 и ∠1 – вертикальные, поэтому ∠3 = ∠1, ∠1 = 30°.
ОТВЕТ: ∠3 = ∠1 = 30°, ∠2 = 130°, ∠4 = 20°.
Геометрия 7 Атанасян Самостоятельная 2
II уровень сложности (ответы)
Ответы на Вариант 1 (2-й ур.)
№ 1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.
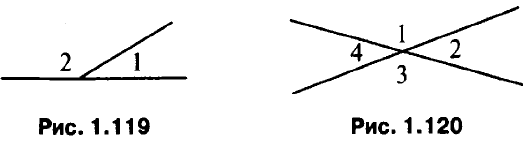
Указание к решению: Пусть ∠1 составляет 0,2∠2, тогда ∠1 = 0,2∠2. Но ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда 0,2∠2 + ∠2 = 180°, ∠2 = 150°, a ∠1 = 0,2 • 150° = 30° (рис. 1.119).
ОТВЕТ: 30° и 150°.
№ 2. Сумма трех углов, образовавшихся при пересечении двух прямых, равна 325°. Найдите остальные углы.
Указание к решению: Пусть ∠1 + ∠2 + ∠3 = 325°, тогда ∠4 = 360° – 325° = 35°, ∠4 = ∠2 как вертикальные, тогда ∠2 = 35°.
∠1 + ∠2 = 180°, ∠4 + ∠3 = 180°, тогда ∠1 = ∠3 = 145° (рис. 1.120).
ОТВЕТ: 145°, 35°, 145°.
№ 3. Даны углы α, β и γ. Известно, что α > β, а γ < β. Найдите среди этих углов тот, смежный с которым будет наибольшим.
ОТВЕТ: Так как α > β, γ < β, то γ < β < α, т. е. наименьшим среди углов α, β, γ будет γ, а смежный с ним угол будет наибольшим среди углов, смежных с углами α, β, γ.
Ответы на Вариант 2 (2-й ур.)
№ 1. Один из смежных углов составляет 0,8 другого. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 составляет 0,8∠2, тогда ∠1 = 0,8∠2. Но ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда 0,8∠2 + ∠2 = 180°, ∠2 = 100°, a ∠1 = 0,8 • 100° = 80° (рис. 1.121).
ОТВЕТ: 80° и 100°.
№ 2. Сумма двух углов, образовавшихся при пересечении двух прямых, равна 78°. Найдите остальные углы.
Указание к решению: Сумма смежных углов равна 180°, поэтому 78° – это сумма вертикальных углов. Но вертикальные углы равны, и получаем, что ∠1 = ∠2 = 39°. ∠1 + ∠3 = 180°, ∠2 + ∠4 = 180°, тогда ∠2 = ∠4 = 141° (рис. 1.122).
ОТВЕТ: 141°, 141°.
№ 3. Даны углы α, β и γ. Известно, что α > β, а γ < β. Найдите среди углов тот, смежный с которым будет наименьшим.
ОТВЕТ: Так как α > β, γ < β, то γ < β < α, т. е. наименьшим среди углов α, β, γ будет γ, а наименьшим среди смежных с ними углов будет угол, смежный с углом α.
Геометрия 7 Атанасян Самостоятельная 2.
III уровень сложности (ответы)
Ответы на Вариант 1 (3-й ур.)
№ 1. 4/7 одного из смежных углов и 1/4 другого составляют в сумме прямой угол. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 и ∠2 – смежные и 4/7∠1 + 1/4∠2 = 90°.
Так как ∠1 + ∠2 = 180°, то ∠2 = 180° – ∠1, тогда 4/7∠1 + 1/4(180° – ∠1) = 90°, ∠1 = 140°, ∠2 = 40°.
ОТВЕТ: 140° и 40°.
№ 2. Сумма вертикальных углов в 2 раза меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.
Указание к решению: Пусть ∠1 и ∠3 – вертикальные, ∠2 – смежный с каждым из углов ∠1 и ∠3, тогда 2(∠1 + ∠3) = ∠2 (рис. 1.123).
Но ∠1 = ∠3, a ∠2 = 180° – ∠1, тогда 2(∠1 + ∠1) = 180° – ∠1, ∠1 = 36°.
ОТВЕТ: ∠1 = ∠3 = 36°.
№ 3. Один из четырех углов, образовавшихся при пересечении двух прямых, в 11 раз меньше суммы трех остальных углов. Найдите эти четыре угла.
Указание к решению: Пусть данные углы – ∠1, ∠2, ∠3, ∠4.
Тогда ∠4 • 11 = ∠1 + ∠2 + ∠3. ∠1 = ∠3 как вертикальные, ∠2 = ∠4 = 180° – ∠1.
Тогда 11(180° – ∠1) = ∠1 + (180° – ∠1) + ∠1, ∠1 = 150°, ∠2 = 30°, ∠3 = 150°, ∠4 = 30° (рис. 1.124).
ОТВЕТ: 30°, 30°, 150°, 150°.
Ответы на Вариант 2 (3-й ур.)
№ 1. Меньший из смежных углов в 4 раза меньше разности этих смежных углов. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 и ∠2 – смежные и 4∠1 = ∠2 – ∠1.
Так как ∠1 + ∠2 = 180°, то ∠2 = 180° – ∠1, тогда 4∠1 = 180° – ∠1 – ∠1, ∠1 = 30°, ∠2 = 150°.
ОТВЕТ: 30° и 150°.
№ 2. Сумма вертикальных углов на 30° меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.
Указание к решению: Пусть ∠1 и ∠3 – вертикальные, ∠2 – смежный с каждым из углов ∠1 и ∠3.
Тогда ∠1 = ∠3, ∠2 = 180° – ∠1, и ∠1 + ∠3 + 30° = ∠2, т. е. ∠1 + ∠1 + 30° = 180° – ∠1, ∠1 = 50° (рис. 1.125).
ОТВЕТ: ∠1 = ∠3 = 50°.
№ 3. Сумма трех углов, образовавшихся при пересечении двух прямых, на 280° больше четвертого угла. Найдите эти четыре угла.
Указание к решению: Пусть данные углы – ∠1, ∠2, ∠3, ∠4, тогда ∠4 + 280° = ∠1 + ∠2 + ∠3. ∠1 = ∠3 как вертикальные, ∠2 = ∠4 = 180° – ∠1.
Тогда 180° – ∠1 + 280° = ∠1 + (180° – ∠1) + ∠1, ∠1 = 140°, ∠3 = 140°, ∠2 = ∠4 = 40° (рис. 1.126).
ОТВЕТ: 40°, 40°, 140°, 140°.
Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 8. Самостоятельная работа № 2 «Перпендикулярные прямые» с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 2. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 7. Поурочные планы
Геометрия 7. Самостоятельные работы
Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 19. Решение задач на применение второго признака равенства треугольников. Самостоятельная работа № 5 с ответами и подсказками к решению (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 5.
Геометрия 7. Контрольные работы
Геометрия 7. Самостоятельные работы
Геометрия 7 класс. Урок 19.
Самостоятельная работа № 5 (задания)
Основная дидактическая цель урока: совершенствовать навыки решения задач на применение второго признака равенства треугольников. Перед решением задач необходимо повторить конспекты: «Треугольник. Равенство треугольников», «ЗАДАЧИ на Признаки равенства треугольников».
I уровень сложности (легкий)
Вариант 1 (уровень 1)
- Дано: СО = OD, ∠C = 90°, ∠D = 90° (рис. 2.120). Доказать: О – середина АВ.
- Дано: АВ = ВС, АК = КС, ∠AKE = ∠PKC (рис. 2.121). Доказать: ΔАКЕ = ΔСКР.
Вариант 2 (уровень 1)
- Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.122). Доказать: АВ = AD.
- Дано: АВ = ВС, МА = РС, ∠АMO = ∠OPC (рис. 2.123). Доказать: ΔАМО = ΔОPC.
II уровень сложности (средний)
Вариант 1 (уровень 2)
- Дано: BD – биссектриса ∠ABC, ∠1 = ∠2 (рис. 2.124). Доказать: АВ = СВ.
- Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.125). Доказать: ΔАВС = ΔADC.
Вариант 2 (уровень 2)
- Дано: О – середина АВ, ∠1 = ∠2 (рис. 2.126). Доказать: ∠C = ∠D.
- Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.127). Доказать: ΔABO = ΔADO.
III уровень сложности (сложный)
Вариант 1 (уровень 3)
- Дано: АВ = СВ, ∠A = ∠C (рис. 2.128). Доказать: AM = CN.
- Дано: AM = МС, АЕ = DC, ∠BDA = ∠FEC (рис. 2.129). Доказать: АВ = FC.
Вариант 2 (уровень 3)
- Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.130). Доказать: АВ = DC.
- Дано: АВ = ВС, АF = КС, ∠DKA = ∠EFC (рис. 2.131). Доказать: AD = ЕС.
Самостоятельная работа № 5
Указания к решению и ОТВЕТЫ
С-5. I уровень сложности (ответы)
Задания и Ответы на Вариант 1 (уровень 1)
№ 1. Дано: СО = OD, ∠C = 90°, ∠D = 90° (рис. 2.120).
Доказать: О – середина АВ.
Доказательство: так как СО = OD, ∠C = 90°, ∠D = 90° по условию задачи, ∠AOC = ∠BOD, то ΔАСО = ΔAOD по стороне и прилежащим к ней углам.
№ 2. Дано: АВ = ВС, АК = КС, ∠AKE = ∠PKC (рис. 2.121).
Доказать: ΔАКЕ = ΔСКР.
Доказательство: так как АВ = ВС, то ΔАВС – равнобедренный с основанием АС. ∠A = ∠C как углы при основании равнобедренного треугольника. ΔАКЕ = ΔСКР по стороне и прилежащим к ней углам (АК = КС, ∠A = ∠C, ∠AKE = ∠PKС).
Задания и Ответы на Вариант 2 (уровень 1)
№ 1. Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.122).
Доказать: АВ = AD.
Доказательство: так как по условию задачи ∠1 = ∠2, ∠3 = ∠4, АС – общая сторона треугольников АВС и ADC, то ΔАВС = ΔADC по стороне и прилежащим к ней углам.
№ 2. Дано: АВ = ВС, МА = РС, ∠АMO = ∠OPC (рис. 2.123).
Доказать: ΔАМО = ΔОPC.
Доказательство: АВ = ВС, поэтому ΔАВС – равнобедренный с основанием АС, и в ΔАВС углы при основании равны (∠A = ∠C). ΔАМО = ΔСРО по стороне и прилежащим к ней углам (МА = PC,∠A = ∠C, ∠AMO = ∠OPC).
Геометрия 7 Атанасян Самостоятельная 5
С-5. II уровень сложности (ответы)
Задания и Ответы на Вариант 1 (уровень 2)
№ 1. Дано: BD – биссектриса ∠ABC, ∠1 = ∠2 (рис. 2.124).
Доказать: АВ = СВ.
Доказательство: BD – биссектриса ∠ABC, поэтому ∠ABD = ∠CBD. ∠1 = ∠2, следовательно, ∠ADB = ∠CDB (если два угла равны, то смежные с ними углы равны). ΔABD = ΔCBD по стороне и прилежащим к ней углам (BD – общая сторона, ∠ABD = ∠CBD, ∠ADB = ∠CDB), следовательно, АВ = СВ как соответствующие стороны равных треугольников.
№ 2. Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.125).
Доказать: ΔАВС = ΔADC.
Доказательство: ΔADO = ΔАВО по стороне и прилежащим к ней углам (АО – общая сторона, ∠1 = ∠2, ∠3 = ∠4). ΔАВС = ΔADC по двум сторонам и углу между ними (AD = АВ как соответствующие стороны равных треугольников, АС – общая сторона, ∠3 = ∠4 по условию задачи).
Задания и Ответы на Вариант 2 (уровень 2)
№ 1. Дано: О – середина АВ, ∠1 = ∠2 (рис. 2.126).
Доказать: ∠C = ∠D.
Доказательство: О – середина АВ, значит, АО = ВО.
ΔАСО = ΔDBO по стороне и прилежащим к ней углам (АО = ВО, ∠AOC = ∠BOD как вертикальные, ∠CAO = ∠DBO, так как смежные им углы 1 и 2 равны). Из равенства треугольников АСО и DBO следует равенство соответствующих углов С и D).
№ 2. Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.127).
Доказать: ΔABO = ΔADO.
Доказательство: ΔADC = ΔАВС по стороне и прилежащим к ней углам (АС – общая сторона, ∠1 = ∠2, ∠3 = ∠4 по условию задачи). ΔADO = ΔАВО по двум сторонам и углу между ними (АО – общая сторона, AD = АВ как соответствующие стороны равных треугольников ADC и ABC, ∠3 = ∠4).
Геометрия 7 Атанасян Самостоятельная 5.
С-5. III уровень сложности (ответы)
Задания и Ответы на Вариант 1 (уровень 3)
№ 1. Дано: АВ = СВ, ∠A = ∠C (рис. 2.128).
Доказать: AM = CN.
Доказательство: ΔABN = ΔСВМ по стороне и прилежащим к ней углам (АВ = СВ по условию задачи, ∠A = ∠C по условию задачи, ∠B – общий). Так как ΔABN = ΔСВМ, то ВМ = BN как соответствующие стороны равных треугольников. Так как BM =BN и AB = АС, то АМ = CN.
№ 2. Дано: AM = МС, АЕ = DC, ∠BDA = ∠FEC (рис. 2.129).
Доказать: АВ = FC.
Доказательство: AM = МС, следовательно, ΔАМС – равнобедренный с основанием АС, а значит, ∠A = ∠C. AD = СЕ, так как AD = АЕ – DE, СЕ = CD – DE, а АЕ = DC. ΔABD = ΔСFЕ по стороне и прилежащим к ней углам (AD = СЕ, ∠A = ∠C, ∠BDA – ∠FEC). Так как ΔABD = ΔCFE, то АВ = FС.
Задания и Ответы на Вариант 2 (уровень 3)
№ 1. Дано: ∠1 = ∠2, ∠3 = ∠4 (рис. 2.130).
Доказать: АВ = DC.
Доказательство: ΔABD = ΔDCA по стороне и прилежащим к ней углам (AD – общая сторона, ∠BAD = ∠CDA, так как ∠BAD = ∠1 + ∠3, ∠CDA = ∠2 + ∠4, a ∠1 = ∠2, ∠3 = ∠4 по условию задачи). Значит, АВ = CD.
№ 2. Дано: АВ = ВС, АF = КС, ∠DKA = ∠EFC (рис. 2.131).
Доказать: AD = ЕС.
Доказательство: ΔАВС – равнобедренный с основанием АС, следовательно, ∠A = ∠C. ΔADK = ΔСЕF по стороне и прилежащим к ней углам (АК = СF, так как АК = AF + FK, CF = СК + FK, а АF = КС по условию задачи; ∠A = ∠C; ∠DKA = ∠EFC). Так как ΔADK = ΔCEF, то AD = ЕС.
Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 19. Решение задач на применение второго признака равенства треугольников. Самостоятельная работа № 5 с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 5. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 7. Поурочные планы
Геометрия 7. Самостоятельные работы
Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и подсказками к решению (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6.
Геометрия 7. Контрольные работы
Геометрия 7. Самостоятельные работы
Геометрия 7 класс. Урок 21.
Самостоятельная работа № 6 (задания)
Основная дидактическая цель урока: совершенствовать навыки решения задач на применение второго признака равенства треугольников. Перед решением задач необходимо повторить конспекты: «Треугольник. Равенство треугольников», «ЗАДАЧИ на Признаки равенства треугольников».
I уровень сложности (легкий)
Вариант 1 (уровень 1)
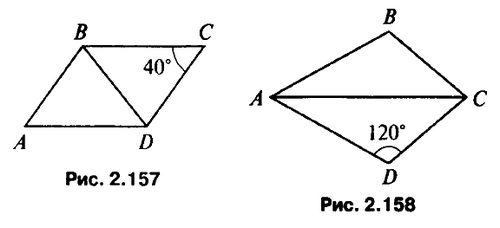
- Дано: АВ = СD, ВС = DA, ∠C = 40° (рис. 2.157).
Доказать: ΔABD = ΔCDB. Найти: ∠A. - На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника. Докажите, что MD = ND.
- В треугольниках АВС и А1В1С1 АВ = А1В1, ∠A = ∠A1, ∠B = ∠B1. Точки D и D1 лежат соответственно на сторонах АС и А1С1, причем CD = C1D1. Докажите, что ΔBDC = ΔB1D1C1. Сравните отрезки BD и B1D1.
Вариант 2 (уровень 1)
- Дано: AD = АВ, CD = CB, D= 120° (рис. 2.158).
Доказать: ΔDAC = ΔBAC. Найти: ∠B. - На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – высота треугольника. Докажите, что MD = ND.
- В треугольниках АВС и А1В1С1 АВ = A1B1, АС = A1C1, ∠A = ∠A1. Точки D и D1 лежат соответственно на сторонах АС и A1C1, ∠DBC = ∠D1B1C1. Докажите, что ΔBDC = ΔB1D1C1. Сравните углы ВDC и B1C1D1.
II уровень сложности (средний)
Вариант 1 (уровень 2)
- Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
- На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.
- В треугольниках АВС и А1В1С1 АВ = A1B1, ∠А = ∠A1, ∠B = ∠B1. На сторонах ВС и В1С1 отмечены точки D и D1 так, что ∠CAD = ∠C1A1D1. Докажите, что: а) ΔADC = ΔA1D1C1; б) ΔADB = ΔA1D1B1.
Вариант 2 (уровень 2)
- Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
- Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.
- В треугольниках DEC и D1E1C1 DE = D1E1, ∠D = ∠D1, ∠E = ∠E1. На сторонах DE и D1E1 отмечены точки P и P1 так, что ∠DCP = ∠D1C1P1. Докажите, что: a) ΔDCP = ΔD1C1P1; б) ΔCPE = ΔC1P1E1.
III уровень сложности (сложный)
Вариант 1 (уровень 3)
- Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
- ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).
- В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.
Вариант 2 (уровень 3)
- Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
- ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).
- В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.
Самостоятельная работа № 6
Указания к решению и ОТВЕТЫ
С-6. I уровень сложности (ответы)
Докажите самостоятельно.
Геометрия 7 Атанасян Самостоятельная 6
С-6. II уровень сложности (ответы)
Задания и Ответы на Вариант 1 (уровень 2)
№ 1. Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
Докажите самостоятельно.
№ 2. На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.
Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и медиана BD является его биссектрисой (рис. 2.160).
2) ΔMBN – равнобедренный с основанием MN, так как МВ = BN (МВ = ВА– МА; BN = ВС – МС, ВА = ВС, МА = NC). BD – биссектриса ΔMBN, и по свойству биссектрисы равнобедренного треугольника она является медианой, т. е. ВО – медиана ΔMBN.
№ 3. В треугольниках АВС и А1В1С1 АВ = A1B1, ∠А = ∠A1, ∠B = ∠B1. На сторонах ВС и В1С1 отмечены точки D и D1 так, что ∠CAD = ∠C1A1D1.
Докажите, что: а) ΔADC = ΔA1D1C1; б) ΔADB = ΔA1D1B1.
Доказательство:
а) ΔАВС = ΔА1В1С1 по стороне и прилежащим к ней углам (АВ = A1B1, ∠A = ∠A1, ∠B = ∠B1 по условию задачи) (рис. 2.161). ΔADC = ΔA1D1C1 по стороне и прилежащим к ней углам (АС = А1С1, ∠C = ∠C1 из равенства треугольников АВС и А1В1С1, ∠CAD = ∠C1A1D1 по условию задачи).
б) Так как ΔADC = ΔA1D1C1, то DC = D1C1, следовательно, равны отрезки BD и B1D1 (ВС = В1С1 из равенства треугольников АВС и А1В1С1). Так как АВ = А1В1, ∠B = ∠B1 из равенства треугольников АВС и А1В1С1 и BD = В1D1, то ΔABD = ΔA1B1D1 по двум сторонам и углу между ними.
Задания и Ответы на Вариант 2 (уровень 2)
№ 1. Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Докажите самостоятельно.
№ 2. Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.
Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и высота BD, проведенная из его вершины к основанию, является и его биссектрисой, т. е. ВО – биссектриса ∠ABC и ∠MBN тоже (рис. 2.163).
2) ΔMBN – равнобедренный с основанием MN (ВМ = ВА + AM, BN = ВС + CN; так как ВА = ВС и АМ = CN, то ВМ = BN). В равнобедренном ΔMBN биссектриса ВО, проведенная из его вершины к основанию, является и его высотой.
№ 3. В треугольниках DEC и D1E1C1 DE = D1E1, ∠D = ∠D1, ∠E = ∠E1. На сторонах DE и D1E1 отмечены точки P и P1 так, что ∠DCP = ∠D1C1P1. Докажите, что: a) ΔDCP = ΔD1C1P1; б) ΔCPE = ΔC1P1E1.
Доказательство:
а) ΔDEC = ΔD1E1C1 по стороне и прилежащим к ней углам (DE = D1E1, ∠D = ∠D1, ∠E = ∠E1) (рис. 2.164).
Так как ΔDEC = ΔD1E1C1, то DC = D1C1. Тогда ΔDCP= ΔD1C1P1 по стороне и прилежащим к ней углам (DC = D1C1, ∠D = ∠D1, ∠PCD= ∠P1C1D1).
б) Так как ΔDEC = ΔD1E1C1, тo EC = E1C1, ∠ECD = ∠E1C1D1.
Так как ∠ECD = ∠E1C1D1, ∠PCD = ∠P1C1D1, a ∠ECP = ∠ECD – ∠DCP, ∠E1C1P1 = ∠E1C1D1 – ∠D1C1P1, ∠ECP = ∠E1C1P1.
Так как ЕС = E1C1 ∠E = ∠E1, ∠ECP = ∠E1C1P1, то ΔPEC = ΔP1E1C1 по стороне и прилежащим к ней углам.
Геометрия 7 Атанасян Самостоятельная 6.
С-6. III уровень сложности (ответы)
Задания и Ответы на Вариант 1 (уровень 3)
№ 1. Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
Докажите самостоятельно.
№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).
Доказательство: ΔМЕК = ΔPFK по двум сторонам и углу между ними (ME = FP, МК = КР по условию задачи, ∠M = ∠P как углы при основании равнобедренного ΔMNP). Следовательно, КЕ= KF.
ΔKEN = ΔKFN по трем сторонам (КЕ = KF; KN – общая сторона; NE = NF, так как NE = MN – ME, NF = PN – PF, a MN = PN, ME = PF). Следовательно, ∠EKN = ∠FKN.
Так как ∠EKN = ∠FKN, то KN – биссектриса угла ∠EKF.
№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.
Доказательство: Так как D – середина основания равнобедренного ΔАВС с основанием АС, то BD – медиана, а значит, и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.167).
∠NBA = ∠CBM как вертикальные.
∠NBD = ∠NBA + ∠ABD, a ∠MBD = ∠MBC + ∠CBD. Так как ∠ABD = ∠CBD, ∠MBC = ∠NBA, то ∠NBD = ∠MBD.
ΔNBD = ΔMBD по двум сторонам и углу между ними (NB = МВ; BD – общая сторона; ∠NBD = ∠MBD).
Задания и Ответы на Вариант 2 (уровень 3)
№ 1. Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
Докажите самостоятельно.
№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).
Доказательство: ΔМЕК = ΔPFK по стороне и прилежащим к ней углам (МК = КР, так как К – середина МР; ∠MKE = ∠PKF по условию задачи; ∠M = ∠P как углы при основании равнобедренного ΔMNP).
Так как ΔМЕК = ΔPFK, то ME = PF, следовательно, EN = FN (EN = MN – ME, FN = PN – PF, a MN = FN как боковые стороны равнобедренного треугольника).
Так как ΔМЕК = ΔPFK, то КЕ = KF. ΔNEK = ΔNFK по трем сторонам (NK – общая сторона, NE = EF, ЕК = ЕК).
№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.
Доказательство: Так как D – середина основания АС равнобедренного ΔАВС, то BD – медиана и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.170).
∠NBA = ∠CBM как вертикальные. Поэтому ∠NBD = ∠MBD (∠NBD = ∠NBA + ∠ABD, ∠MBD = ∠MBC + ∠CBD, a ∠NBA = ∠CBM, ∠ABD = ∠CBD).
ΔBDM = ΔBDN по стороне и прилежащим к ней углам (BD – общая сторона, ∠NBD = ∠MBD, ∠BDM = ∠BDN).
Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 7. Поурочные планы
Геометрия 7. Самостоятельные работы
Что такое смежные углы? Какие у них свойства?
Определение.
∠1 и ∠2 — смежные углы
Сколько смежных углов образуется при пересечении двух прямых?
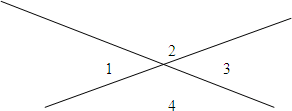
При пересечении двух прямых образуется четыре пары смежных углов:
∠1 и ∠2, ∠3 и ∠4,
∠1 и ∠3, ∠2 и ∠4
Но, так как ∠1 =∠4, ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.
Свойство смежных углов.
Сумма смежных углов равна 180º.
Задачи.
1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.
Дано:
∠AOC и ∠BOC — смежные,
∠AOC на 42º больше, чем ∠BOC
Найти: ∠AOC и ∠BOC.
Решение:
Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.
Имеем уравнение:
х+х+42=180
2х=180-42
2x=138
x=69
Значит, ∠BOC= 69º, ∠AOC=69+42=111º.
Ответ: 69º и 111º.
2) Найти смежные углы, если их градусные меры относятся как 4:5.
Дано:
∠1 и ∠2 — смежные,
∠1 : ∠2= 4:5
Найти:∠1 и ∠2
Решение:
Пусть k — коэффициент пропорциональности. Тогда ∠2 =4kº , ∠1=5kº. Так как сумма смежных углов равна 180º, ∠1 +∠2=180º.
Имеем уравнение:
4k+5k=180
9k=180
k=20
Значит, смежные углы равны 4∙20=80º и 5∙20=100º.
Ответ: 80º и 100º.
3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.
Дано: AB и CD — прямые, O — точка их пересечения,
∠AOD в 5 раз больше, чем ∠BOD
Найти: ∠AOD, ∠BOD
Решение:
При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD — смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.
Имеем уравнение:
x+5x=180
6x=180
x=30
Значит, ∠BOD=30º, ∠AOD=5∙30=150º.
Ответ: 30º и 150º.
Могут ли смежные углы быть равными?
Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.
Вывод:
угол, смежный с прямым, есть прямой угол.
Могут ли два смежных угла быть тупыми? Острыми?
Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.
Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.
Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).
(831) 247 47 55 eduVdom.com
Геометрия ( Справочник )Стереометрия ( Справочник )Математика ( Справочник )Русский язык ( Справочник )Физика ( Справочник )
Геометрия:
Введение в геометрию
Отрезок, луч, угол Отрезок Луч и полуплоскость Угол Измерение отрезков Измерение углов Смежные и вертикальные углы. Перпендикулярные прямые
Треугольники Треугольник и его элементы Признаки равенства треугольников Свойства равнобедренного треугольника. Третий признак равенства треугольников.
Основные геометрические построения Окружность Основные задачи на построение
Параллельные прямые Определение параллельных прямых Признаки параллельности двух прямых. Свойства параллельных прямых
Сумма углов треугольника Теорема о сумме углов треугольника Соотношения между сторонами и углами треугольника. Неравенство треугольника Расстояние от точки до прямой Признаки равенства прямоугольных треугольников
Четырехугольники Определение четырехугольника Параллелограмм. Расстояние между параллельными прямыми Диагонали и признаки параллелограмма Прямоугольник Ромб Квадрат Теорема Фалеса. Средняя линия треугольника Трапеция Центральная и осевая симметрии Пропорциональные отрезки
Тригонометрические функции острого угла. Теорема Пифагора Тригонометрические функции острого угла. Определения Теорема Пифагора Основные тригонометрические тождества Значения тригонометрических функций некоторых углов Зависимости между сторонами и углами прямоугольного треугольника Решение прямоугольных треугольников
Прямоугольные координаты Координатная ось Прямоугольная система координат на плоскости Расстояние между точками Координаты середины отрезка Определение тригонометрических функций для любого угла от 0 до 180°
Векторы Понятие вектора Сложение и вычитание векторов Умножение вектора на число Координаты вектора Скалярное произведение векторов
Подобие Определение подобных треугольников Признаки подобия треугольников Подобие произвольных фигур
Окружность Касательная к окружности Центральные и вписанные углы Вписанная и описанная окружности Пропорциональность отрезков хорд и секущих окружности
Решение треугольников Теорема синусов и теорема косинусов Решение треугольников
Многоугольники. Длина окружности Ломаная Многоугольник Правильный многоугольник Длина окружности Длина дуги окружности. Радианная мера угла
Площади плоских фигур Понятие площади Площадь прямоугольника Площадь параллелограмма Площадь треугольника и ромба Площадь трапеции Площадь правильного многоугольника Площадь круга и кругового сектора
Контакты
eduVdom.com+7 910 874 73 73+7 904 064 04 04Больше контактов...Оставить отзыв...Используемые источники:
- http://www.treugolniki.ru/smezhnye-ugly/
- https://wiki.eduvdom.com/subjects/geometry/смежные_и_вертикальные_углы