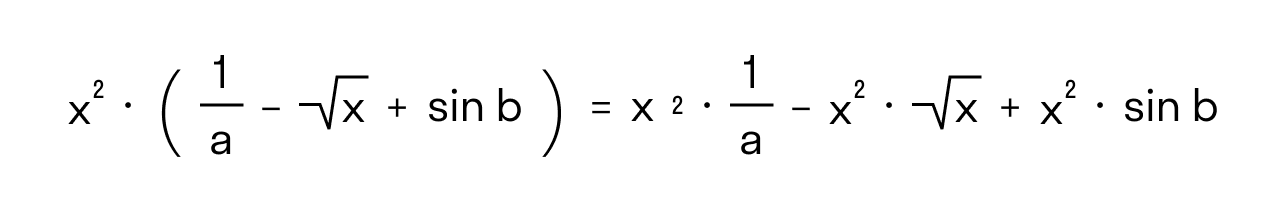Урок математики
2 класс
Тема: Порядок выполнения действий. Скобки.
Провела: Боровинская Л.Ю
Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.
УУД:
Познавательные :учащиеся научатся соблюдать порядок действий при вычислениях; находить значения выражений, содержащих скобки;
Регулятивные: использовать графические модели при решении задач;
Коммуникативные: слушать собеседника и вести диалог;
Личностные: оценивать себя и товарищей.
Ход урока:
-
Мотивация (самоопределение) к учебной деятельности.
Прозвенел звонок и смолк-
Начинается урок.
Вы за парты тихо сели,
На меня все посмотрели.
-Сегодня у нас необычный урок. Мы отправляемся в Тридевятое государство, а отнесут нас туда волшебные пятерки. Чем лучше вы напишите, тем быстрее мы окажемся в сказке.
(Звучит мелодия « В гостях у сказки»)
2. Каллиграфическая минутка.
-Письмо цифры “5” (Ведем от верхней границы клетки линию до середины, прописываем — овал: закругление и еще раз закругление, отрываем руку и прописываем верхний элемент цифры).
3. Устный счет.
-Сказка начинается. В некотором царстве, в Тридевятом государстве жили-были Иван-Царевич (рис.1) и Василиса Прекрасная (рис.2). Однажды Василиса исчезла. Иван Царевич потужил, погоревал и отправился на поиски. Но куда идти? Где искать? Кто похитил Василису? Мы узнаем, если правильно будем считать устно.
а) (Примеры читают по-разному)
12-3= 73-3 = 60-40 =
8+5 = 84-80= 20 + 30=
б) Устные задачи.
На Земле 4 океана, а материков на 2 больше. Сколько материков на Земле?
в) — Найдите “лишнее” число. Расположите числа в порядке убывания.
35 73 33 40 13 23
В порядке убывания: 73 35 33 23 13
-Теперь перевернем карточки. Что получилось? (КОЩЕЙ)
-Кто же похитил Василису? (рис.3) (КОЩЕЙ)
— Иван-Царевич отправился в путь дальше. Но Кощей послал Змея Горыныча (рис.4) погубить Ивана-Царевича. Нужно победить все три головы, Змея.
-Для этого нужно выполнить задания:
1 уч.(у доски):
— Поставь знаки
12 -6 … 14 – 5 12 + 10… 10 +12
-А пока мы решим задачи в стихах:
1.Сеть тяну, рыбу ловлю
Попалось немало:
7окуней, 10 карасей,
1 ершок – и того в горшок.
Уху сварю, всех угощу.
Сколько рыбок я сварю?
2. Пара лошадей пробежала 20 км. Сколько км пробежала каждая?
3. Определите время (Показываю модель часов)
— Свалили мы Змеиные головы? Молодцы!
— Идет Иван-Царевич. Видит, густой лес. Избушка на курьих ножках стоит, а в ней Баба Яга (рис.5). Баба Яга говорит Ивану: “Если сделаешь то, что раньше никогда не делал, скажу, где Кощей живет. Поможем Ивану-Царевичу?”
В конце урока каждый из вас оценит свою работу.
5.Актуализация и фиксирование индивидуального затруднения в пробном действии.
(На доске записаны примеры.)
12-2+8=18
12-2+8=2
-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?
-Какое равенство верно? (Первое.)
— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
-А кто уже знает, в каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 2 и 8, а затем из 12 вычесть их сумму.)
6.Выявление места и причины затруднения.
— Мы поняли, как нужно решать эти примеры. А как показать это другим и Б.-Яге?
— Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия в некоторых примерах.)
7.Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)
— О чём сейчас говорили? (О порядке выполнения действий.)
— Какая тема урока? (Порядок выполнения действий.)
— Значит, надо научиться обозначать в записи порядок действий и показать эти умения Б.-Яге)
8.Поиск решения проблемы.
(Учитель выставляет карточку с примером)
10 – 5 + 2
— Прочитайте. Какое действие надо выполнить первым? (Сложение)
— Почему? (Оно выделено)
— Как называется то, что выделено? (Сумма)
— Из числа вычитаем сумму. Для того, чтобы показать, что первым действием будет сложение, в математике используют скобки. По-другому наш пример можно записать так:
10 – (5 + 2)
— Что показывают скобки? (Что данное действие надо выполнять первым).
Давайте вычислим:
10 – 5 + 2 = 3
— Можно не указывать порядок действий и укоротить запись, записав результат, полученный в скобках, карандашом.
— Какие действия выполняют первым, если есть скобки?
( Действия в скобках)
-Посмотрите, чем отличаются столбики примеров?
8-3+4=9 8-(3+4)=1
18-8+9=19 18-(8+9)=1
(В первом столбике нет скобок, а во втором есть.)
— Зачем же они нужны?
-Как выполняли действия в первом столбике? (По порядку.)
-Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? (Сначала выполним действие в скобках.)
-Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? ( В первом столбике мы выполняли действия по порядку, а во втором сначала в скобках.)
-Что нам поможет указать на порядок выполнения действий? (Скобки.)
-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками. (Сначала выполняются действия в скобках, а потом по порядку)
9.Первичное закрепление с проговариванием во внешней речи
— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.
Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.
— Кто уже сможет рассказать правило Б- Яге?
-Попробуем применить наше новое знание на практике.
№ 1 (с. 38).
(Коллективное выполнение с комментированием.)
Физкультминутка
Ветер тихо клен качает,
Вправо, влево наклоняет.
Раз наклон и два наклон,
Зашумел листвою клен.
(Ноги на ширине плеч, руки за голову.
Наклоны туловища вправо и влево.)
Видишь бабочка летает,
(Взмахи руками.)
На лугу цветы считает:
(Считать пальчиком.)
Раз, два, три, четыре, пять —
(Хлопки в ладоши.)
Ох, считать не сосчитать!
(Прыжки на месте.)
Шесть, семь, восемь, девять, десять —
(Хлопки в ладоши.)
Даже мудрая пчела (Взмахи руками.)
Сосчитать бы не смогла!
(Считать пальчиком.)
10.Самостоятельная работа в парах с самопроверкой по эталону.
№2 (с. 38).
-Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку. (Не получим.)
-Измените порядок действий. Какое действие выполним первым? (Сложение.)
-Вычислите. Получился ли у вас нужный результат? (Да.)
—Поставьте скобки.
(Остальные примеры разбираются аналогично. Следует обратить внимание учащихся на то, что, если скобки не меняют порядок действий, их можно не ставить.)
11.Включение в систему знаний повторение.
№3 (с. 38).
(Один ученик выполняет на доске с комментированием, остальные— в тетрадях.)
№4 (с. 38).
-Рассмотрите рисунок.
( Составьте задачу по первому решению. (В лодке плыли 5 детей и 1 взрослый. Сколько всего человек плыло в лодке ?)
( Составьте задачу по второму решению. (В лодке было 6 человек. На берег вышли 2 человека. Сколько человек осталось и лодке?)
Можно ли задачи назвать обратными? (Нет.)
-Решите задачи.
(Ученик, решивший задачу первым, записывает решение и ответ на доске. Проверка. Тем, кто справится с заданием быстрее других, дополнительно можно предложить составить ко второй задаче обратные задачи.)
-Молодцы! Справились с заданием. Баба Яга сказала, как найти Кощея.
-Добрался Иван-Царевич до Кощея. А он встретил Ивана-Царевича такими словами: “Раз ты смог добраться до меня, выполни мое задание и Василиса твоя! Если не выполнишь, голова с плеч!”
№5
(Самостоятельное выполнение. Проверка по образцу на экране)
Ну, Иван, забирай Василису — сказал Кощей. “Только сначала догадайся, где она. У меня 4 башни. Первая башня пустая. Василиса не в самой высокой. Где она?”
12. Рефлексия.
— Хорошо! Спасли мы Василису? Да! Вот видите, как хорошо мы потрудились! Это потому, что все вместе работали. Для общего дела старались. Спасибо всем, все хорошо потрудились (перечисляю).
— Итак, что нового мы узнали на пути к спасению Василисы?
— В чём испытывали трудности?
Коллективная проверка.
— Оцените свою работу.
13.Домашнее задание (по выбору).
Математика — это точная, но сложная наука, которая присутствует в окружающих явлениях и сопровождает нас всю жизнь. Математическая сказка – особый прием в педагогике, который помогает ребенку понять азы математики и легче усваивать информацию в дальнейшем. Специалисты утверждают, что в форме сказки малышу полезнее всего постигать законы мироустройства, знакомиться с нормами поведения и даже изучать математические основы.

Почему именно сказка?
Сказка – уникальное средство для обучения ребенка. Это метафора, поняв которую, малыш сможет применять общее правило в разных ситуациях. Сказка с математическим содержанием – это приключение, героями которого становятся цифры, арифметические знаки, геометрические фигуры или знакомые детям персонажи из народных сказок. Сюжет содержит понятия о времени, количестве, величинах, формах и осложнен математическими проверками и задачами.
Математическая сказка играет важную роль в обучении, например:
- способствует формированию собственного математического и логического мышления;
- выполняет познавательную функцию;
- учит выполнять простейшие арифметические действия;
- знакомит с цифрами, математическими понятиями, терминами;
- объясняет взаимосвязь между предметами и явлениями окружающего мира.
Основы науки в сказках объясняются ненавязчиво, легко и доступно для ребенка, поэтому педагоги успешно используют сказки как в подготовке дошкольников, так и в программе по математике для начальной школы.

Математические сказки для дошкольников
Привить ребенку усидчивость и любовь к числам не всегда легко, а сказки про цифры позволяют сделать это в игровой форме. Лучше подобрать сказку с рисунком – так малышу легче представить необычных героев. Попробуйте нарисовать простенькие иллюстрации сами или привлеките к процессу ребенка.
Ниже приведены примеры сказок для дошкольников.

Ноль и Единица
В одном городе жили цифры от 0 до 9. Они всегда спорили и хвастались друг перед другом, кто больше или старше. Цифры даже придумали для себя знаки «>» и «<», так им легче было хвастаться. Некоторые цифры очень грустили, особенно доставалось Нолику и Единичке, ведь они были самыми маленькими, и их постоянно дразнили: «Малыши!».
Однажды Ноль и Единица сидели и плакали от обиды, что они ничего не могут сделать против старших цифр. Тогда они взялись за руки, чтобы было не так обидно. Ноль с Единицей шли по улице, а другие цифры как-то странно на них смотрели — как будто снизу. Друзья дошли до витрины магазина и увидели в отражении, что они стали большими, как никогда! Даже больше, чем цифра 9! Так получилось число 10. Другие цифры посмотрели на 10 и поняли, что если объединиться и действовать сообща, то можно стать сильнее и больше.

Спор геометрических фигур
Заспорили Квадрат, Треугольник и Круг, кто из них важнее.
— Я важнее, ведь у меня больше всех углов – целых четыре! — сказал Квадрат.
-Ну и что, зато мои углы острее, чем твои, значит, я лучше! – возразил Треугольник.
— У меня хоть углов нет, зато я могу катиться по дорожке, а вы будете до вечера перекатываться на своих углах, – ответил на это Круг.
— Ну, можешь ты катиться, а дальше что? Никому фигура без углов не нужна, – сказал Квадрат, а Треугольник его поддержал, – даже дом не построишь без квадрата или треугольника: стены да окна у дома квадратные, а крыша – треугольная. А круга там и в помине нет!
Тут Круг говорит:
— Посмотрите на небо, там солнце, оно самое важное на небе, а оно на круг похоже! Значит, я тоже важен! Луна тоже круглая, а без нее ночью темно.
Посмотрели Квадрат с Треугольником на небо: действительно, солнце – как круг. И луна ночью круглая. Поняли фигуры, что они все важны.
— Да, — сказал Квадрат, — правда, без круга тоже никак. А вокруг нас, оказывается, столько круглых, квадратных и треугольных предметов.
Задание: А вы сможете найти такие предметы у себя дома?

Сказки для начальной школы
В начальной школе творческие способности детей лучше всего проявляются в групповых или самостоятельных проектах. Одно из таких заданий в 3 классе – математическая сказка. Можно сочинить свою собственную историю о цифрах, геометрических фигурах или использовать готовую, оформив ее иллюстрациями от руки, сделать вместе с родителями презентацию на компьютере из слайдов или придумать другой вариант. Сказка может быть написана в прозе или в стихах. Вот лишь несколько примеров математических сказок для 3 – 4 кл.
Сказка о ленивом нуле
В маленькой стране Цифрии жили цифры. Все были трудяги, только Ноль был пузатый и ленивый.
Как-то узнали товарищи, что в соседнюю страну Арифметию на службу требуются цифры, чтобы составлять уравнения и задачи для учеников. Цифры обрадовались, что теперь могут работать на благо детей, и отправились в путь. Только дорога был нелегкая. Путь пролегал под палящим солнцем, а впереди было 4 реки, которые нужно было перейти, а заодно потренироваться в арифметике.
Вот дошли они до первой реки под названием Сложение. Подбежали циферки к реке попить, а та сказала: «Я дам вам воды, но сначала вы встанете по парам и сложитесь, чтобы получилось новое число». Все цифры быстренько встали по парам, выполнили задание, а одна цифра зазевалась, ей достался Ноль. Как ни складывалась цифра с нулем, сумма не изменилась, пришлось уйти, не попив воды.
Шли цифры дальше, солнце уже в зените, воды хочется. Дошли до второй реки – Вычитание. Снова все бросились к воде, а женский голос им говорит: «Я дам вам напиться, но сначала встаньте по парам, да вычтите из большего меньшее, чтобы получилось новое число». Все быстро поделились на пары, сделали, что просят, но уже другая цифра в этот раз промедлила, ей достался Ноль. Вычла она ноль, а число не изменилось. Осталась цифра без воды, а Ноль вообще не волновался – ему было лень.
Пошли цифры дальше, дошли до реки Умножение. Снова река попросила выполнить задание – встать по парам, да помножиться друг на друга. Все быстро выполнили просьбу, но снова одной цифре не повезло, она умножилась на ноль и тоже стала нулем. Цифра даже расплакалась, так ей обидно стало, что из-за нуля все страдают.
Наконец, дошла компания до последней реки – Деление. Солнце уже не пекло, но задание все же пришлось выполнить – правила есть правила. Цифрам нужно было поделиться друг на друга так, чтобы получилось число больше единицы. Тут цифрам пришлось подумать, кто на кого должен делиться. К тому же, переругались все – никто не хотел делиться на ноль.
Дошли цифры до страны Арифметии, прибыли на службу, но пожаловались правительнице на ленивца, из-за которого все страдают. Правительница успокоила их и сказала, что всем цифрам найдется работа, даже Ноль пригодится в уравнениях или примерах. А чтобы остальные на него не злились, наделила она Ноль особой способностью: если он встает справа от любой цифры, то увеличивает ее в 10 раз.
Так Ноль перестал лениться и почувствовал себя нужным, а товарищи больше на него не обижались. Но делиться на него до сих пор никто не хочет, чтобы не зазнавался и помнил, как он своей ленью друзей подвел.

Логическая сказка о верблюдах
Однажды к отцу пришли три сына и попросили отпустить их во взрослую жизнь:
— Кланяемся мы тебе, батенька, но просим твоего разрешения пойти жить отдельно – выросли мы уже.
Отец согласился, только назвал одно условие:
— Я вас отпущу, но прежде вы возьмете себе верблюдов из моего стада. Старший сын возьмет половину, средний сын – одну треть, а младший сын – одну девятую. Если поделите семнадцать верблюдов, как я сказал, – идите с миром.
Пытали братья поделить верблюдов так и эдак, да никак не получалось. Расстроились молодцы, видать не хочет отец их отпускать. Пошли братья к мудрому старцу за советом. Старец нашел решение:
— Я отправлю своего верблюда вам на помощь. Это легкая задача, даже верблюд сможет поделить ваше стадо.
Братья послушали мудреца, поставили верблюда в стойло к остальным, как тут же поняли, что теперь-то верблюдов стало восемнадцать! Разделили они верблюдов, как велел отец: старшему сыну половину, среднему – треть, младшему – девятую часть, и вдруг обнаружили, что в стойле остался один верблюд. Думали, что с ним делать, решили отдать его мудрецу в благодарность за то, что помог им решить задачу. Пришли братья к старцу, привели верблюда, а старец говорит:
— Поставьте его в стойло, я ему уже корм приготовил.
Удивились молодцы: как это старец догадался, что они приведут верблюда? А тот засмеялся и ответил:
— Мой верблюд меня предупредил, что вернется домой, как только поможет вам решить задачу.
Вопросы:
- Сколько верблюдов забрал каждый сын?
- Почему сначала задачу нельзя было решить, а потом получилось?
- Почему после деления верблюдов между братьями остался один верблюд?
Математические сказки для 5 класса
Сказочная математика применяется не только в обучении младших школьников – ученики 5 класса тоже сочиняют математические сказки. Вот несколько примеров.

Хитрый король
В одном королевстве правил хитрый король, который старался обмануть своих подданных да нажить себе денег. Однажды он созвал свою армию и сказал:
— Воины! Вы славно служите мне, я хочу вас отблагодарить. Я увеличиваю ваше месячное жалование на 20%!
Воины обрадовались, закричали: «Ура, да здравствует король!».
А король продолжил:
— Но только на один месяц. Вы будете получать больше денег ровно один месяц, а потом я снова понижу ваше жалование на 20%, и все будет, как было раньше.
Воины пожали плечами, да только порадовались тому, что хотя бы один месяц они будут получать больше.
«Да здравствует король, — говорил один старый воин друзьям, — раньше я получал 10 тыс., а в этом месяце получил 12 тыс., а потом снова буду получать 10, я ничего не теряю».
Но прошел месяц, а воин, как и другие, получил не 10 тыс. ровно, а 9 тыс. 600 рублей.
«Как же так? Ведь король обещал снизить жалование 20% и сказал, что мы ничего не потеряем!».
Расстроились воины, пошли к мудрецу. Мудрец выслушал подданных короля, улыбнулся и поведал, как король обхитрил свою армию: он поднял жалование на 20% от 10 тыс. – это 2 тыс., а потом снизил на 20% от 12 тыс. – это 2 тыс. 400 руб. В итоге воины стали получать даже меньше, чем раньше.
Расстроились товарищи, решили провести хитрого короля.
— Ваше Величество, – сказали они, — Вы были правы, когда повысили нам жалование, а потом понизили, сказав, что это одно и то же. Мы преданно служим Вам, поэтому просим сделать это еще раз, только теперь наоборот: сначала понизить нам жалование на 20%, а потом опять поднять на 20%.
Король не стал возражать и согласился на предложение.
Задание: Посчитайте, сколько денег получит воин через месяц? А через 2 месяца? Кто оказался хитрее?

Сказка о смешанных числах
В стране Математике был Город Правильных Дробей. В этом городе можно было встретить разных жителей. Кто-то из них был маленький — 1/7 или 1/9, кто-то большой — 2/3 или 5/6.
Жители города считали себя очень красивыми. Они действительно были красивые: верх у этих дробей был утонченный, легкий, а низ был больше размером, но смотрелась такая дробь очень гармонично. От того, что дроби были красивыми, они называли себя Правильными.
Как-то в городском парке дроби сидели у фонтана, мило беседовали, как вдруг все замерли и уставились на странную дробь. Верх у нее был толстый, тяжелый, а низ такой тоненький, что дробь еле-еле держалась на ногах.
— Вы только посмотрите, какая уродина! – брезгливо сказала красавица 4/5.
Дробь 4/5 правда была красива, тут не поспоришь.
— Да, сидела бы лучше дома, что дробей пугать! – поддержала подругу 8/9. Она была не такая красивая – с длинным хвостом, но зато большая, поэтому позволяла себе такие вольности.
— Неправильная ты какая-то, — добавила дробь 5/6.
А дробь эта действительно была неправильная, непропорциональная, звали ее 7/6. Бедняжку постоянно дразнили из-за нетипичной внешности, и она каждый раз плакала, В этот раз 7/6 не выдержала: решила уйти из города и отправиться в странствие.
Собрала дробь 7/6 узелок в дорогу и пошла. Шла долго, но в итоге подошла к воротам города. Дробь постучалась в ворота, а когда ей открыли, перед странницей стояло число 1, а за ручку оно держало маленькую дробь 1/9.
— Здравствуйте, меня зовут дробь 7/6, я хотела бы остановиться в вашем городе. Не приютите ли вы меня? – спросила робко Неправильная дробь. – Меня высмеивали и унижали в Городе Правильных Дробей, мне некуда больше пойти.
Странное создание улыбнулось и сказало:
— Добро пожаловать в Город Смешанных Чисел, милая Неправильная дробь!
И тут произошло что-то необычное, чего дробь 7/6 даже не смогла сразу понять: целое число подняло на руки маленькую дробь и превратилось… в Неправильную дробь 10/9!
— Ничего себе, так Вы – тоже Неправильная дробь?! – воскликнула 7/6.
— Вообще я – Смешанное Число, но могу превращаться в Неправильную дробь. Хотя быть Смешанным Числом гораздо удобнее. Попробуй тоже, – ответила дробь 10/9.
Дробь 7/6 закрыла глаза, сосредоточилась и… почувствовала, как стала большой, а кто-то взял ее за руку. Оказалось, теперь она не 7/6, а Смешанное Число 1 и 1/6.
Так несчастная дробь, которую все дразнили, нашла место, где стала счастливой, и забыла про Город Правильных Дробей. Да и понятия о красоте в Городе Смешанных Чисел совсем другие.

«Сказка ложь, да в ней намек…»
Детство любого ребенка сложно представить без сказки. Мир воображения безграничен, поэтому сказка – уникальный инструмент не только для постижения жизненных законов, но и для обучения наукам. Вымышленные истории с математическим содержанием позволяют детям усваивать материал с практической стороны, не зацикливаясь на теоретической части правил.
Для сказки не существует возрастных рамок, ведь по мере развития ребенка истории наполняются новым смыслом, адекватным его возрасту. Вот почему сказки успешно применяются педагогами и родителями в дошкольной подготовке малышей и обучении математике младших и даже старших школьников.
Понятие раскрытия скобок
В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.
Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.
Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:
- 2(3 + 4) = 2 * 3 + 2 * 4.
Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.
Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.
В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:
- знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
- произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).
Раскрытие скобок также можно рассматривать шире.
Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:
- 5 + (-3) — (-7) = 5 — 3 + 7.
Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:
- 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1
Первое правило раскрытия скобок
Рассмотрим выражение:
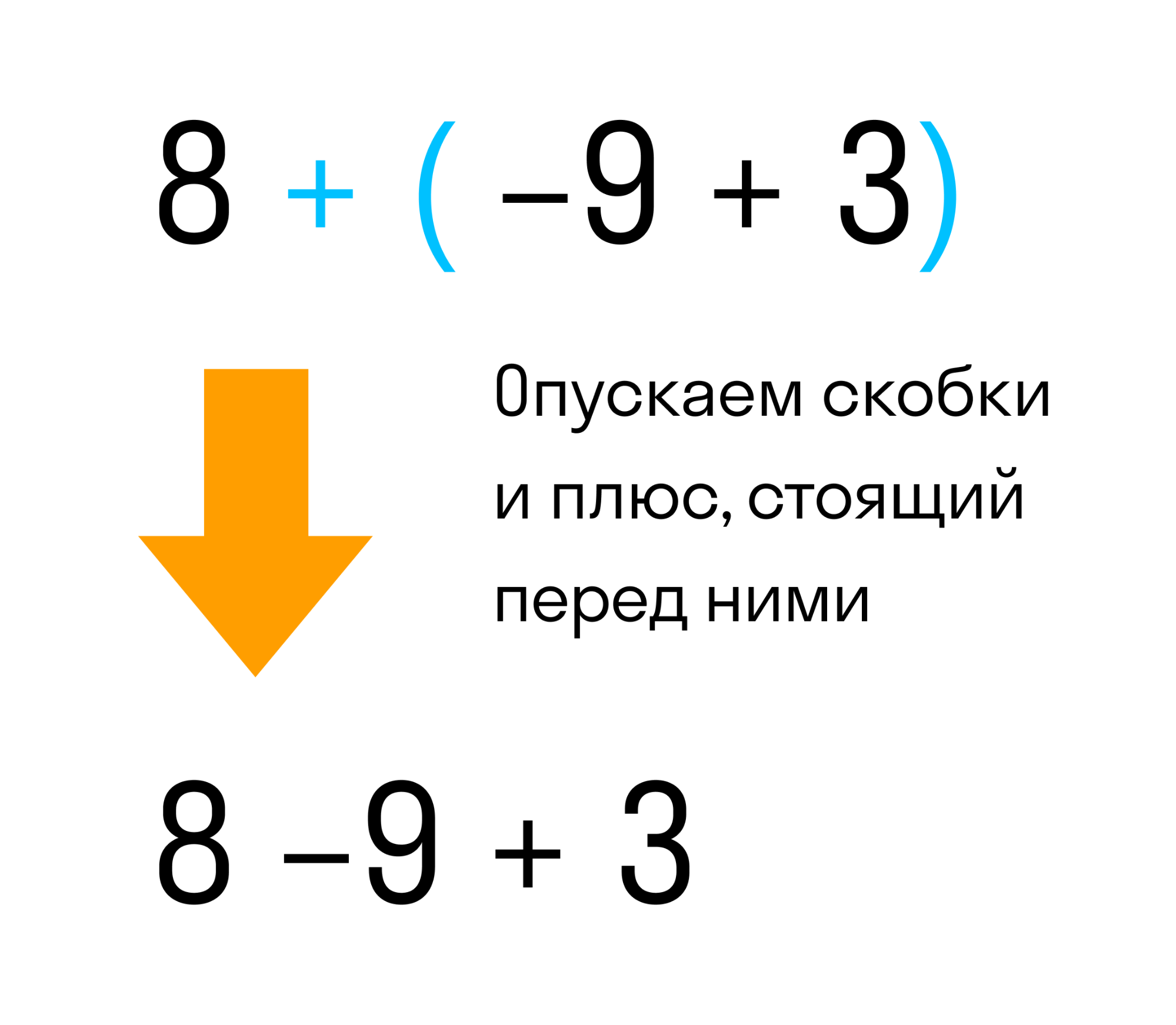
- 8 + (−9 + 3)
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
Первое правило раскрытия скобок
Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.
Формула раскрытия скобок
(a − b) = a — b
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
- 8 + (−9 + 3) = 2
- 8 − 9 + 3 = 2
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
- 8 + (−9 + 3) = 8 − 9 + 3
- 2 = 2
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Как рассуждаем:
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
- 8 + (−3 − 1) = 8 − 3 − 1
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Как рассуждаем:
Перед скобками стоит плюс, значит применим то же правило:
- 6 + (−2) = 6 − 2
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
- 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
- 3a + (−4b) = 3a − 4b
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
- 2 + (−3 + 1) + 3 + (−6)
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
- 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки 6 + (−3) + (−2)
Как рассуждаем:
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
- 6 + (−3) + (−2) = 6 − 3 − 2
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
- 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении (−7)
Как рассуждаем:
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
- (−7) = −7
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Как рассуждаем:
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
- −
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Второе правило раскрытия скобок
Здесь рассмотрим второе правило раскрытия скобок. Звучит так:
Второе правило раскрытия скобок
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.
Формула раскрытия скобок
−(a − b) = −a + b
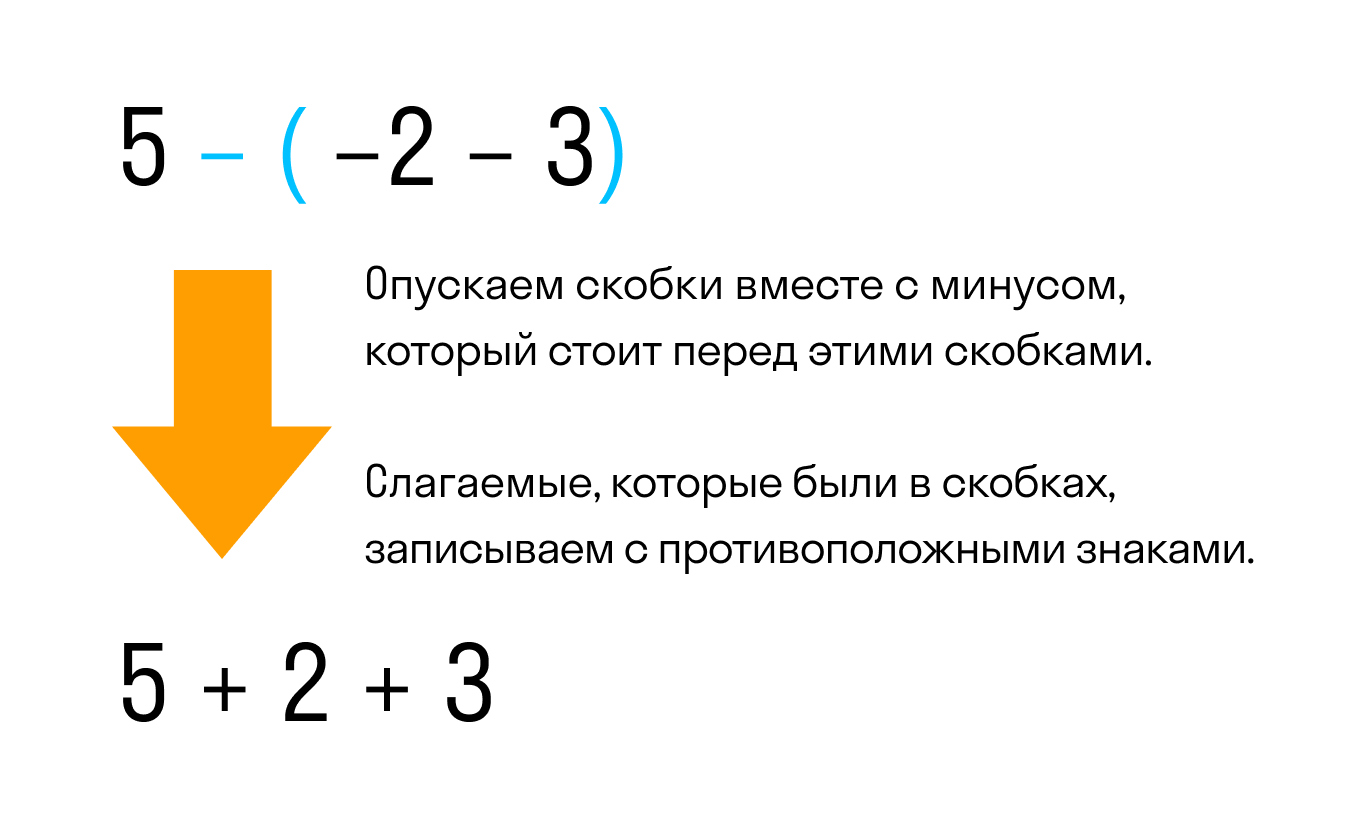
Например, раскроем скобки в выражении 5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.
- 5 − (−2 − 3) = 10
- 5 + 2 + 3 = 10
Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:
- 5 − (−2 − 3) = 5 + 2 + 3
- 10 = 10
Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
18 − (−1 − 5) = 18 + 1 + 5
Пример 2. Раскрыть скобки −(−6 + 7)
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
−(−6 + 7) = 6 − 7
Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)
Как рассуждаем:
Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:
−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2
Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10
Как рассуждаем:
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
a − (3b + 3) + 10 = a − 3b − 3 + 10
Другие правила раскрытия скобок
Правило раскрытия скобок при делении
Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.
Формула раскрытия скобок
(a + b) : c = a/c + b/c.
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:
- (x + 2) : 2/3 = (x + 2) * 3/2.
Далее умножим скобку на число:
- (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.
Правило раскрытия скобок при умножении:
Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.
Формула раскрытия скобок
a(b + c) = ab + ac
Пример 1. Раскрыть скобки 5(3 − x)
Как решаем:
В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:
Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.
Пример 2. Упростить выражение: 5(x + y) − 2(x − y)
Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.
Таблица с формулами раскрытия скобок
Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.
| Правила раскрытия круглых скобок вида (-a), в которых находится одночлен | |
| При сложении: b + (-a) = b — a b — (-a) = b + a (-a) + b = -a + b | При умножении: (-a)b = -ab a(-b) = -ab (-a)(-b) = ab |
| Правила раскрытия круглых скобок, в которых находится многочлен |
| Скобки убирают, знаки всех слагаемых в скобках не меняют, если:
a + (b — c + d) = a + b — c + d
(a+b-c)+d=a+b-c+d |
| Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:
a — (b — c + d) = a — b + c — d
-(a + b — c) + d = -a — b + c + d |
| Раскрытие круглых скобок при умножении одночлена на многочлен |
| a + b(c + d — f + e) = a + bc + bd — bf + be a + b(c + d — f + e) = a + bc + bd — bf + be -a(b + c — d) + f = -ab — ac + ad + f |
| Раскрытие круглых скобок при умножении многочлена на многочлен |
| (a + b)(c — d) = a(c — d) + b(c — d) = ac — ad + bc — bd (-a + b)(c + d) = -a(c + d) + b(c + d)= -ac — ad + bc + bd |
| Раскрытие круглых скобок при возведении многочлена в степень |
| (a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2 |
Скобка в скобке
В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:
- упростить выражение 7x + 2(5 − (3 x + y)).
Чтобы успешно решать подобные задания, нужно:
- внимательно разобраться со скобками — какая в какой находится.
- раскрывать скобки последовательно, начиная с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.
Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))
Как решаем:
Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y).
Теперь раскроем вторую скобку, внешнюю:
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y.
Упростим получившееся выражение:
- 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y = 7x + 10 − 6x − 2y.
Приведем подобные:
- 7x + 10 − 6x − 2y = x + 10 − 2y
Готово!
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок раскрытия скобок согласован с порядком выполнения действий:
- возвести многочлены в скобках в натуральную степень;
- слева направо провести умножение и деление;
- когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.
Пример 1. Раскрыть скобки и упростить выражение:
-(2a + 5b) + (3a — 2b + 1) — (2a + 4) = -2a — 5b + 3a — 2b + 1 — 2a — 4 = (-2a + 3a — 2a) + (-5b — 2b) + (1 — 4) = -a — 7b — 3
Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a — 7) — (a + (5a — 4)) — отрицательно.
Доказательство:
33(2a — 7) — (a + (5a — 4)) = 3(2a — 7 ) — (a + 5a — 4)= 6a — 21 — a — 5a + 4 = (6a — a — 5a) + (-21 + 4) = -16/p>
Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.
Задачи для самостоятельного решения
На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.
Задание 1. Раскройте скобки в выражении: 2 + (6 + 3) + 2 — (1 + 1)
Задание 2. Раскройте скобки в выражении: — 21 + 14 + (-1 + 5) — 11 + ( 3 + 2)
Задание 3. Раскройте скобки в выражении: 3 * (-4m + 3n — 5)
Задание 4. Раскройте скобки в выражении: -(12a — 5b — 2)
Задание 5. Раскройте скобки в выражении: 3(x — 9)
Задание 6. Раскройте скобки:
Задание 7. Раскройте скобки:
МБОУ « Шибашская СОШ»
Алькеевского муниципального района РТ
« Скобки»
(Разработка урока по математике во 2классе)
Учитель начальных классов
Гараева Резеда Бариевна
Предмет: математика
Класс – 2
УМК «Перспектива»
Тема урока: « Скобки»
Тип урока: урок «открытия» новых знаний
Цели:
познакомить с порядком выполнения арифметических действий в выражениях со скобками, содержащими сложение и вычитание.
развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.
совершенствовать навыки решения составных задач; развивать мышление и внимание.
Задачи:
-формировать умение работать в группе, находить общее решение, умение аргументировать своё предложение;
-формировать умения самостоятельно выделять и формулировать познавательную цель всего урока и отдельного задания;
-строить логическое рассуждение.
— развивать логическое мышление, умение анализировать, делать выводы, — развивать речь детей; — развивать самостоятельность учащихся, умение преодолевать трудности в учении, используя проблемные ситуации, самостоятельные упражнения.
— Совершенствовать вычислительный навык
— Воспитывать культуры поведения.
Приобретаемые навыки детей: активизация познавательной и самостоятельной деятельности, обобщение знаний.
Формы работы: фронтальная, индивидуальная, парная, групповая.
Используемое оборудование: — ПК, проектор, карточки с заданием для индивидуальной и парной работы, карточки с ответами; примеры для темы урока, карточки с ответами и буквами для темы урока, презентация к уроку, учебник математики и рабочие тетради. (авторы: Г.В.Дорофеев, Т.Н.Миракова).
Ход урока
I. Мотивация к учебной деятельности
1.Организационный момент.
Итак, друзья, внимание
Ведь прозвенел звонок.
Садитесь поудобнее
Начнем скорей урок.
— Работать сегодня мы будем коллективно и в парах. Вспомните правила работы в парах.(Прислушиваться к мнению соседа, работать дружно, помогать друг другу)
В конце урока каждый из вас оценит свою работу.
II. Актуализация
(На доске записаны примеры.)
40-5+7=42
40-5+7=28
-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?
-Какое равенство верно? (Первое.)
— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
— В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 5 и 7, а затем из 40 вычесть их сумму.)
Какого знака не хватает в этом числовом выражении, чтобы получился ответ 28? (Скобок)
– Где их надо поставить?
III. Выявление места и причины затруднения.
— Мы поняли, как нужно решать эти примеры. А как показать это другим?
— Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия в некоторых примерах.)
IV Усвоение новых знаний.
– Попробуйте разными способами вычислить значение выражения
10 – 4+2
(Ответы учащихся 8 и 4)
– Какого знака не хватает в этом числовом выражении, чтобы получился ответ 4? (Скобок)
– Где их надо поставить?
Работа по учебнику, с. 32 – чтение параграфа.
— Какой вывод можно сделать о решении выражений со скобками?
— Если в выражении есть скобки, то сначала вычисляют значение выражения в скобках.
— А если нет скобок? (Если нет скобок, то в выражении действия выполняют по порядку слева направо).
— Посмотрим на схемы, которые будут помогать нам решать такие примеры. Обратите внимание, что на схемах указан порядок, в котором выполняются действия, мы также будем указывать цифрами этот порядок.
Слайд
V. Физкультминутка
Вы, наверное, устали?
Ну тогда все дружно встали.
Ручками похлопали
Ножками потопали.
Покрутились, повертелись
И за парты все уселись.
VI . Первичное закрепление.
VII. Закрепление нового материала.
а) Из учебника (с. 32) зачитывается правило: все читают про себя; вслух 2 учащихся; хором.
Действия, записанные в скобках, выполняются первыми.
б) Решение выражений.
Стр. 32 №1(1,2) – коллективная работа. Дети по цепочке записывают примеры и объясняют их решение.
Самостоятельная работа в тетрадях- с. 32 №1 (3) Проверяют
Самостоятельная работа на доске. Решают 2 учащихся
4-1+2=1 8-5+1=2 12-5+4=3 6-4+9=11
Контроль над усвоением новой темы. Работа по карточкам, работает весь класс. Проверяет карточки . (7+9)+2=
16- (9-4)=
(20-10)+8=
VII Самостоятельная работа в парах с самопроверкой .
№2 (с. 38). -Решите пример.
. Какое действие выполним первым? (Сложение.)
-Вычислите. Получился ли у вас нужный результат? (Да.)
—Поставьте скобки.
(Остальные примеры разбираются аналогично. Следует обратить внимание учащихся на то, что, если скобки не меняют порядок действий, их можно не ставить.)
VIII. Работа в «Рабочей тетради».
Откройте тетрадь Стр. 37 задания № 1-3
IX Самостоятельная работа (разноуровневые задания).
— Перед вами карточки, на них выражения. Решите эти выражения самостоятельно.
Взаимопроверка ( по слайду)
X Рефлексия учебной деятельности на уроке.
Мне удалось…
Мне понравилось…
Я порадовался за …
Я могу похвалить себя за…
С каким настроением заканчиваем урок?
(нарисуйте лицо человечка: грустное или весёлое)
XI Итог урока
-Какие цели мы достигли на уроке?
На этом уроке мы узнали, что использование скобок в выражении всегда меняет порядок действий, а значение выражения может оставить без изменений.
Домашнее задание (по выбору).
-
Учебник: № 6 (с. 39).
Тетрадь с печатной основой: № 27 (с. 37)
МКОУ Красносельская основная школа
Урок математики
2 класс
Тема: Порядок выполнения действий. Скобки.
УМК «Школа России»
Автор : учитель начальных классов
Иванова А.Ф.
2017г.
Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; совершенствовать вычислительные навыки; закрепить умение работать в группах и в парах на уроках математики.
УУД:
Познавательные:учащиеся научатся соблюдать порядок действий при вычислениях; находить значения выражений, содержащих скобки;
Регулятивные: использовать графические модели при решении задач;
Коммуникативные: слушать собеседника и вести диалог;
Личностные: оценивать себя и товарищей.
Ход урока:
1.Самоопределение к учебной деятельности
Цель: мотивировать учащихся к учебной деятельности
Учитель приветствует учащихся, проверяет их готовность к уроку. Учащиеся приветствуют учителя и проверяют свою готовность к уроку.
2.Актуализация знаний
Цель: повторение пройденного материала.
Учитель обращает внимание учащихся на доску, где прикреплено изображение ранца (портфеля).
-Ребята, а что вы взяли сегодня на урок математики, кроме учебника и школьных принадлежностей?(предполагаемый ответ: знания.)
Несколькимучащимся предложено показать свои умения у доски, а остальным на индивидуальных карточках . В заданиях включены выражения на сложения и вычитания, сравнения величин.
Карточка №1
12-6__14-5
40мм__3см 1мм
7+8+3=
14+6=
20-10=
Учащиеся выполняют задания по карточкам и у доски. Обосновывают выбор правильного ответа. Производят самоконтроль. Отвечают на вопросы учителя.
3.Постановка проблемы
Цель: выявить и зафиксировать в речи причину затруднении.Согласовать тему урока и цели
(На доске записаны примеры.)
20-9+8=19
20-9+8=3
-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?
-Какое равенство верно? (Первое.)
— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
— В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму.)
В ходе диалога с учащимися появляется проблема:как выделить действие, выполняемое первым. После примеров, приведенных учащимися, учитель сообщает о том, что в математике используют скобки.
— О чём сейчас говорили? (О порядке выполнения действий.)
— Какая тема урока? (Порядок выполнения действий.)
-Какова цель нашего урока? (Узнать, зачем нужны скобки; научиться решать примеры со скобками; научиться расставлять скобки в выражениях .)
Цели формулируются учащимися с помощью учителя, прикрепляются на доску.
4.Проектирование и фиксация нового знания.
Учитель вместе с учащимися формулируют правило: действия, записанные в скобках, выполняются первыми.
На слайде два примера:
10-(5+2)
(10-5)+2
-Чем похожи эти выражения, а чем различаются?(Похожи-набором чисел и знаков, различаются-порядком скобок)
Учащиеся составляют алгоритм решения выражении со скобками с помощью учителя.
-Одинаковое ли значение получилось в этих выражениях?(нет)
После данной работы учащиеся формулируют вывод: скобки изменяют порядок действий в выражениях и их значения .
Физкультминутка
Раз, два, три — вперёд наклон,
Раз, два, три — теперь назад. (Наклоны вперёд, назад.)
Головой качает слон —
Он зарядку делать рад. (Подбородок к груди, затем голову запрокинуть назад.)
Хоть зарядка коротка,
Отдохнули мы слегка. (Дети садятся.)
Головою три кивка
Раз — подняться, потянуться, (Потянулись.)
Два — согнуться, разогнуться, (Прогнули спинки, руки на поясе.)
Три — в ладоши три хлопка, (Хлопки в ладоши.)
Головою три кивка. (Движения головой.)
На четыре — руки шире, (Руки в стороны.)
Пять — руками помахать, (Махи руками.)
Шесть — на место сесть опять. (Присели.)
5.Первичное закрепление нового материала.
— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.
Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.
-Попробуем применить наше новое знание на практике.
Учащимся предлагается решить выражения из учебника. Несколько учащихся комментируют свои действия, придерживаясь алгоритма.
Вывод: в выражениях суммы скобки не влияют на значение.
Самостоятельная работа в парах
Учащимся предлагается работа в парах на карточках. Задание: расставить скобки в выражениях так, чтобы значения в выражениях стали верными.
Карточка №2
4-1+2=5
8-5+1=2
Вывод: если скобки не меняют порядок действий, их можно не ставить.
6.Рефлексия учебной деятельности на уроке.
Цель:
1)Зафиксировать новое содержание, изученное на уроке.
2)Организовать рефлексию и самооценку учениками собственной учебной деятельности.
Учащимся предложено выполнить задание, выбрав его из трех разных по сложности.
Три человека, выбравшие разные по сложности задания(легкое, средней сложности и повышенной сложности) работают за доской.
Карточка №3
*Решить пример: (12+6)-8
**Расставить скобки 5+9-7=7
***Поставить> < =
(10-6)+3__5+(15-9)
После обсуждения выполненных заданий, учитель предлагает учащимся вернуться к целям урока, побуждает высказать мнение, все ли поставленные задачи были выполнены.
Учащимся предложено оценить работу на уроке используя цветовые сигналы.