Фрагмент технологической карты урока по математике на тему: «Точка. Прямая линия. Кривая линия. Отрезок. Луч.»
Преподаватель: Карасева Л.П.
Ейск, 2021 г.
Тема урока: «Точка. Прямая линия. Кривая линия. Отрезок. Луч»
Цель: формирование представлений у учащихся о начальных геометрических понятий «точка», «кривая линия», « прямая», «отрезок». Подготовить к пониманию необходимости специальных приёмов действий для проведения прямой линии. Учить распознавать их.
Личностные УУД: 1)выражать свое мнение, точку зрения; 2)проявлять положительное отношение к уроку, 3) понимать необходимость в учении; 4)проявлять самостоятельность в различных видах деятельности.
Познавательные УУД: 1) ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; 2)добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке; 3)анализировать, сравнивать, сопоставлять, обобщать факты.
Регулятивные УУД: 1) определять и формулировать цель и задачи на уроке; 2) умение осуществлять самоанализ своей деятельности; 3)вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; 4)высказывать своё предположение.
Коммуникативные УУД: 1) сотрудничать со сверстниками; 2) оказывать взаимопомощь сверстникам; 3) оформлять свои мысли в устной форме; 4) слушать и понимать речь других; 5) совместно договариваться о правилах поведения и следовать им; 6) совершенствовать работу в группах, парах, классом.
№ п/п
Этап урока
Деятельность учителя
Деятельность учащегося
Формируемые УУД
2
Актуализация фиксирование индивидуальных затруднений в пробном действии
Отступаем одну клетку вниз от числа.
-Ребята, я вам бужу читать задание, ваша задача решить его и ответ записать к себе в тетрадь. Числа записываем в строчку, через запятую, пропуская одну клетку.
-
Найдите сумму чисел 3 и 4. ( 7)
-
Уменьшите 10 на 2. ( 8 )
-
Увеличьте 4 на 2. ( 6 )
-
1 слагаемое — 5, 2 слагаемое – такое же. Чему равна сумма? ( 10 )
-
10 без 1. ( 9 )
Давайте проверим с вами данную работу.
Устный счёт
-Ребята, посмотрите на слайд. Кто это такой? В какой сказке мы познакомились с этим персонажем?
Катится колобок и тренируется в счете. И мы с вами сейчас потренируемся и проведем устный счет.
1) хором посчитаем от 1 до 10
2) от 8 до 2
3) сколько пальцев на 2-х руках?
4) сколько лап у одной собаки?
5) какое число при счете идет девятым?
6) какое число на 1 больше, числа 5?
7) какое число является предыдущим для числа 3?

9) 1 слагаемое – 5, 2 слагаемое – 2, чему равна сумма этих чисел?
10) в одной коробке 5 карандашей, а другой – ни одного. Сколько всего карандашей в двух коробках?
(Во время выполнения задания контролирую работу учащихся.)
(При выполнении задания в случаи неверных ответов задаю наводящие)
-Молодцы! Не допустили ни одной ошибки
Прекрасно работают на уроке ….
Учащиеся записывают числа в строчку, через запятую.
7
8
6
10
9
Отвечают хором на вопросы устного счета
10
4
9
6
2
8
7
5
Личностные УУД (1)
Познавательные УУД (1)
Регулятивные УУД(1)
3
Выявление места и причины затруднения
-Итак, сейчас мы с вами отправимся в путешествие на волшебном паровозе, но путешествие не легкое, на нашем пути будут появляться трудности, но мы с ними справимся!
Посмотрите на доску. Что на ней изображено?
Все ли они одинаковые?
Назовите и покажите те геометрические фигуры, которые вам знакомы.
Для того чтобы их изобразить, что рисовали?
О чем же будем говорить на уроке?)
Это и будет темой нашего урока.
Фигуры и линии
Нет
Квадрат, круг, треугольник
Линии и точки
о линиях и точках
Личностные УУД (1)
Познавательные УУД (1)
Регулятивные УУД(1)
4
Построение проекта выхода из затруднения
— У каждого из вас, на парте есть карандаш и листочек бумаги. Возьмите карандаш и поставьте его на лист.
А теперь поднимите карандаш, что у нас осталось на листе?
Этот след и есть точка – геометрическая фигура.
В стране Геометрии жила-была точка. Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям. Посмотрите, какие это были линии.
-На что похожи прямые линии?
-Сколько прямых линий?
— На что похожи кривые линии?
— Сколько кривых?
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!
-Очень интересно сталь точке посмотреть на неё. Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На её месте появился луч.
-Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.
-Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила опять на луч.
-И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
-Вот так маленькая точка смогла изменить жизнь больших линий.
-Ребята, какие же геометрические фигуры живут в стране геометрии?
Учащиеся слушают мини сказку о геометрических фигурах.
Прямые и кривые
Похожи на натянутые верёвочки
2
Которые не натянуты
3
Точка, прямая линия, кривая линия, луч, отрезок.
Личностные УУД (1)
Познавательные УУД (1,3)
Регулятивные УУД (3,4)
КоммуникативныеУУД(3,4)
5

— Откройте учебник. Посмотрите на рисунок на стр.40 . Расскажите, чем прямая линия отличается от кривой.
-Что вы запомнили о прямой линии, луче, отрезке?
— Как начертить прямую линию?
— Как начертить отрезок?
— Прочитайте задание на полях на стр.40. Как узнать, какой отрезок самый длинный.
— Посчитайте и скажите, какой отрезок самый длинный.
— Какой отрезок самый короткий?
Учащиеся работают с учебником.
Прямая линия натянута, кривая-нет.
Провести по линейке линию
Поставить две точки и соединить их
Посчитать клетки линии
Синий
Красный
Личностные УУД (3)
Познавательные УУД(1)
Регулятивные УУД(2,3,4)
Коммуникативные УУД(3,4,5)
6
Первичное закрепление с проговариванием во внешне речи
— Рассмотрите рисунок на стр.41.
Найдите и покажите на рисунке кривые линии, отрезки, лучи.
Физминутка
Математику люблю.
Спину ровно я держу.
Вправо, влево наклоняюсь,
Как прямая, выправляюсь.
Руки в стороны раздвину,
Вверх ладошки подниму
И отрезок покажу.
Раз присядем, два присядем
И на место тихо сядем.
Давайте вместе с вами начертим отрезок, проверяйте свой чертеж по-моему, который на доске.
Теперь начертим луч, прямую линию, кривую линию и начертим точку.
Учащиеся работают по рисунку на странице 41.
Учащиеся выполняют упражнения физминутку за учителем
Чертят в тетради все изученные раннее фигуры.
Личностные УУД (3)
Познавательные УУД(1)
Регулятивные УУД(2,3,4)
Коммуникативные УУД(3,4)
7
Самостоятельная работа с самопроверкой по принятому эталону
Итак, ребята вам необходимо будет выполнить самостоятельную работу.
Вам необходимо разделить линии на группы. Это прямые линии и кривые. В первых квадратах вам необходимо написать номера прямых линий, а во-вторых квадратах номера кривых линий.
Учащиеся подписывают карточки и выполняют самостоятельную работу.
Личностные УУД (3)
Познавательные УУД(1)
Регулятивные УУД(2,3,4)
Коммуникативные УУД(3,4)
Тема: «Точка. Кривая линия. Прямая линия. Отрезок. Луч».
Возраст обучающихся: подготовительная группа
Форма организации занятия: занятие-путешествие
Тип занятия: изучение нового материала и первичное закрепление знаний.
Цель занятия:
создать условия по формированию представлений о точке, линии, прямой, отрезке, луче; уметь находить на чертеже геометрические фигуры
Задачи:
Образовательные:
- сформировать первичные представления о точке, линии, прямой, отрезке, луче; о их сходстве и различии;
- совершенствовать умения выполнять простейшие геометрические построения;
Развивающие:
- развивать умение грамотно называть луч, прямую, отрезок;
- развивать творческое математическое мышление посредством введения эвристических вопросов; воображения,
- развивать речь, коммуникативные качества;
Воспитательные — воспитывать познавательный интерес к математике.
Интеграции ОО: «Познавательное развитие», «Социально-Коммуникативное развитие», «Речевое развитие».
Методы организации занятия:
- Словесные методы обучения (беседа
- Методы практической работы.
- Метод игры (игра-путешествие)
- Наглядный метод обучения (иллюстрация, демонстрация)
- Метод проблемного обучения (постановка проблемных вопросов, создание проблемных ситуаций)
- Метод наблюдения.
Оборудование: магнитная доска, магниты.
Демонстрационный материал:
- Карточки с изображением незнакомого дошкольникам геометрического материала.
- Иллюстрации основных геометрических фигур
Раздаточный материал:
- Картинки с задачами
- Детские билеты на ракету
- «Волшебные» карандаши (по количеству детей).
- Карточки «Соедини точки» — с геометрическими фигурами (по количеству детей).
1 этап — организационный
Результат деятельности этапа: определение уровня внимания, активности, восприятия, настроя детей на предстоящее занятие.
Здравствуйте, ребята! Посмотрите, что у меня в руках. Да, это глобус- модель нашей Земли. На нашей планете очень много стран и городов. Чтобы их увидеть мы путешествуем по нашей земле. А как мы можем добраться до других городов, на чем? (полететь на самолете, поплыть на пароходе, на лодке, поехать на поезде, машине, можно даже на велосипеде)
Сегодня мы отправимся в небольшое путешествие в волшебную страну под названием Геометрия. В эту необычную страну можно попасть с помощью необычных билетов, их дают только тем, кто разгадает небольшие задачки (работа по карточкам).
Билеты получены, можно отправляться в путь.
Физминутка
Один, два, три, четыре, пять (ходьба на месте)
В космос мы летим опять (соединить руки над головой)
Отрываюсь от земли (подпрыгнуть)
Долетаю до луны (руки в стороны, покружиться)
На орбите повисим (покачать руками вперед-назад)
На планету мы спешим (ходьба на месте)
2 этап — изучение нового учебного материала
Результат деятельности этапа: осознанное усвоение обучающимися нового учебного материала и первичное закрепление новых знаний
Итак мы прибыли в страну Геометрия. Посмотрите на ее жителей (показываю, рассматриваем геометрические фигуры, назовите их; спрашиваю знакомы ли с объёмными геометрическими фигурами, попробуйте назвать их).
Здесь живет самый маленький житель – Точка. Это геометрическая фигура. (Работа на доске. На доске начерчены точка, кривая линия, прямая линия, отрезок, луч).
Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (Линии на доске).
-Какие это линии? (Ответы детей).
-Прямые линии, ребята, похожи на натянутые веревочки, а веревочки, которые не натянули – это кривые линии. Сколько прямых на доске? (2). Сколько кривых? (2).
-Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца. Я бесконечная!» (Показываю изображение прямой на доске).
-Очень интересно стало точке посмотреть. Сама-то точка малюсенькая. Вышла она и не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч (Показываю изображение луча).
Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало. Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч. И на месте луча появился отрезок. У него уже были начало и конец (Показываю изображение отрезка).
-Понравилась сказка? (Ответы детей). Что узнали о прямой линии? (Она бесконечная) Покажите ее на доске.
-Что узнали о луче? (У него есть начало, но нет конца) Покажите ее на доске
-Что узнали об отрезке? (У него есть начало и конец). Покажите ее на доске
Практическая работа по карточкам
-Давайте посмотрим. Сколько здесь точек?
-Какое задание мы можем сделать с этим множеством точек?
-Правильно, проведите по точкам линии, чтобы получить картинку.
-Давайте посмотрим, что у вас получилось.
-Что вы видите на карточках? (квадраты)
— Сколько их? (3)
-С помощью чего мы получили форму геометрических фигур?
-Одинаковы ли они по размерам? (нет)
—Разукрасьте самый большой квадрат синим цветом, самый маленький желтым цветом, средний по размеру – красным.
-Какого цвета квадрат слева от красного, какой – справа.
-Ребята, как Вы думаете, как можно определите длину прямых сторон? (Ответы детей).
-Что значит определить «на глаз»? (Не измеряя). Есть разные мерки, какие вы помните? (пядь, локоть, сажень)
Для того, чтобы не было путаницы, люди придумали общую мерку – сантиметр. С помощью чего мы можем измерить стороны нашего квадрата? (линейки). Давайте измерим длину квадрата. Что вы заметили? (все стороны равны)
3 этап – итоговый
Результат деятельности этапа: самооценка обучающимися собственной деятельности; определение перспектив развития творческой деятельности в данной образовательной области.
Итак, мы встретились с уже знакомыми жителями страны Геометрии. И познакомились с новыми.
-С чем мы сегодня познакомились?
-Что такое точка? (геометрическая фигура, покажи)
-Что такое линия? (нет ни начала, ни конца, покажи)
— Что такое луч? (есть начало, нет конца, покажи)
— Что такое отрезок? (есть начало и конец, покажи)
-Наше путешествие подошло к концу. Пора отправляться обратно в путь!
Один, два, три, четыре, пять (ходьба на месте)
В космос мы летим опять (соединить руки над головой)
Отрываюсь от земли (подпрыгнуть)
Долетаю до луны (руки в стороны, покружиться)
На орбите повисим (покачать руками вперед-назад)
И опять домой спешим (ходьба на месте)
Скажем до свидания, до новых встреч в стране Геометрия.
Вот мы снова в нашем детском саду в своей группе.
Понравилось ли вам наше путешествие?
В какое путешествие хотели бы отправится еще раз?
А теперь мы попрощаемся с нашими гостями.
Плюсы и минусы
В древности у одного математика было трое учеников. Когда они в совершенстве овладели всеми арифметическими действиями, учитель призвал их и сказал:
– Теперь, когда вы достигли некоторых вершин в математике, пришла пора применить знания на практике, в жизни. Идите же и считайте, чего в мире больше – плюсов или минусов.
Ушли ученики, и пришли ровно через три года, как и договаривались.
– Ну, вот ты,- обратился он к первому ученику,- скажи, чего же в мире больше: плюсов или минусов?
– Конечно же, плюсов. Я встретил умную, красивую, богатую жену. У нас прекрасный дом, сады, чудесные фрукты. У меня за это время родилось двое замечательных детей. И вообще, я считаю, что минусы бывают только в математике, в жизни их вообще не существует.
– Ну, а ты что насчитал? – с грустью обратился он к другому своему ученику.
– Я считал… Все время считал… Золото, разные драгоценности, деньги. Но меня ограбили. Кругом одни негодяи и жулики.
– Ну а как насчет моего задания? Чего больше: плюсов или минусов?
– Какие там плюсы? Вы их когда-нибудь видели в жизни? На каждом шагу одни только минусы.
Учитель погрустнел еще больше, махнул рукой и ничего не ответил.
– А ты что успел подсчитать? – спросил он с некоторой надеждой у своего третьего ученика.
– Я, учитель, ничего не успел. Видел я и плюсы, и минусы. Видел, что плюсы приносят людям радость, а минусы – горе. И мне захотелось сделать так, чтобы в жизни людей было как можно больше плюсов и как можно меньше минусов.
– Но такого не знает математика, – воскликнул учитель. И, помолчав, добавил:
– А всё-таки – это отличное действие. Больше плюсов, меньше минусов – ради этого стоит жить. Молодец, ты здорово усвоил мою науку!
А что вы думаете по этому поводу, ребята?
Путешествие по стране геометрии
Однажды Совёнок услышал незнакомое слово «геометрия». Ему стало очень интересно, что это такое, и он побежал к маме – Мудрой Сове. Мама Сова взяла лист бумаги и карандаш и нарисовала там точку и прямую линию.
– Это точка, – сказала она.
– Точка, – повторил за ней Совёнок.
Мама Сова нарисовала теперь две точки и провела через неё черту (линию).
– Смотри внимательно, Совенок, это линия. Прямая линия. Попробуй, нарисуй и ты такую прямую линию, вот тебе линейка.
Совёнок очень обрадовался, когда у него получилась прямая линия и даже быстро сочинил вот такую песенку:
Прямая линия у нас
Нарисовалась в первый раз!
– Теперь я знаю, что такое геометрия. Она рисует прямые линии. Мудрая Сова засмеялась.
– Не торопись, Совёнок, геометрия изучает не только линии, посмотри: табуретка стоит слева от стула, а стул – справа от табуретки. А вот стоят мальчик и девочка. Скажи: кто из них стоит слева, а кто справа? А вот две точки, расположенные по разные стороны от прямой линии:
– Покажи, какая из них слева от прямой, какая справа?
– Знаю, знаю, – закричал Слонёнок, – геометрия изучает, кто стоит справа, а кто слева! Мудрая Сова покачала головой и продолжила свой рассказ:
– Геометрия ещё может очень много, например, помогает строить дома. Посмотри в окно, видишь, строится дом. Над землёй уже поднялись два этажа, и строители возводят третий. Строителям помогает подъёмный кран. Он поднимает с земли большие плиты – перекрытия и подаёт их строителям. Под тяжестью груза стальной трос туго натянулся. Вот тебе еще прямая линия. Она протянулась точно сверху вниз. Такую линию называют вертикальной. Совёнок всё понял и на радостях придумал новую песенку:
Вот верёвочка моя!
Привязал к ней камень я,
И верёвка моментально
Натянулась вертикально!
– Строители часто используют в своей работе такую верёвочку с грузиком, -продолжала Сова.
– Для чего? – спросил Совёнок.
– Для того, чтобы проверить, вертикально ли стоит стена дома, не наклонилась ли она в какую-нибудь сторону. Если стена наклонилась, то верёвочка с грузиком пойдёт не по стене. Строители же должны стену поставить вертикально. Иначе дом может упасть.
Как родилась линия
В стране Геометрия жила-была маленькая точка. Это была очень красивая красная точка. Однажды она подумала:
– Как мне хочется иметь много друзей! Отправляюсь-ка путешествовать и поищу себе подружек.
Только вышла красная точка за калитку, как на встречу ей тоже точка идёт, только зелёная. Подходит зелёная точка к красной и спрашивает, её куда та идёт.
– Иду искать друзей. Вставай со мной рядом и идём вместе путешествовать.
Через некоторое время встречают они синюю точку. Идут по дороге друзья – точки, и с каждым днём их становится всё больше и больше. И наконец, их стало так много, что выстроились они в один ряд, плечом к плечу и получилась линия. Когда точки идут прямо, получается линия прямая. Когда неровно, криво, – получается кривая линия.
Сказка об отрезке
Жил-был Карандаш. Был он очень любознательный и хотел всё знать. Увидит незнакомую линию и непременно спросит:
– Как эта линия называется?
Вышел однажды Карандаш на прямую линию и пошёл по этой прямой. Шёл, шёл по прямой линии, долго шёл. Устал. Остановился и говорит:
– Долго ли я ещё буду идти? Скоро ли конец прямой?
Засмеялась Прямая:
– Эх ты, Карандаш! Ведь ты не дойдёшь до конца: разве ты не знаешь, что у прямой нет конца?
– Тогда я поверну назад, – сказал Карандаш. – Я, наверное, пошёл не в ту сторону.
– И в другую сторону не будет конца. У линии совсем нет концов. Она бесконечна…
– И Прямая даже пропела про себя песенку:
Без конца и края
Линия прямая!
Хоть сто лет по ней иди,
Не найти конца пути!
Опечалился Карандаш, узнав, что у линии совсем нет концов.
– Как же быть? Что же мне так и придётся идти и идти без конца?
– Ну, если ты не хочешь идти без конца, то отметь на прямой две точки, -подсказала Прямая.
– Ура! – закричал Карандаш. – Появились два конца, теперь я могу гулять по Прямой линии от одной точки до другой. Что же получилось на Прямой? Как это называется?
– Это мой отрезок, – улыбнулась Прямая линия.
– Отрезок прямой, отрезок прямой, – с удовольствием повторял Карандаш, прогуливаясь по отрезку от одного конца до другого. (Он был так рад, что от усталости не осталось и следа.)
Приключения точки
Жила-была Точка. Она хотела всё знать. Увидит незнакомую линию и непременно спросит:
– Как эта линия называется? Длинная она или короткая?
Подумала однажды Точка: «Как же я смогу всё узнать, если всегда буду жить на одном месте? Отправлюсь-ка я путешествовать!» Сказано – сделано. Вышла Точка напрямую линию и пошла по этой линии.
Шла-Шла по прямой линии. Долго шла. Устала. Остановилась и говорит:
– Долго ли я ещё буду идти? Скоро ли конец прямой линии?
– Эх, ты, Точка! Ведь ты не дойдёшь до конца: разве ты не знаешь, что у прямой нет конца?
– Тогда я поверну назад, – сказала Точка. – Я, наверное, пошла не в ту сторону.
– И в другую сторону не будет конца. У прямой линии совсем нет концов.
Опечалилась Точка:
– Как же быть? Что же, мне так и придётся идти, идти без конца?
– Можно позвать на помощь Ножницы, – посоветовала Прямая. Тут, откуда ни возьмись, появились Ножницы, щёлкнули перед самым носом и разрезали Прямую.
– Ура! – закричала Точка. – Вот и конец получился! А теперь сделайте, пожалуйста, конец, с другой стороны.
– Можно и с другой, – послушно щёлкнули Ножницы.
– Как интересно! – воскликнула Точка. – Что же из моей прямой
получилось? С одной стороны – конец, с другой стороны конец. Как это
называется?
– Это отрезок, – сказали Ножницы. – Можно нарезать много отрезков и даже разной длины: одни короткие, другие длинные. И разбросать их можно, как захочется.
– Ножницы быстро-быстро защелкали.
Посмотри, что получилось. Если нарисовать кружочек, получится солнышко с разными лучиками, – робко ответила Точка. – А как можно точно определить, какой из отрезков самый длинный и какой самый короткий?
– Нужно позвать на помощь Циркуль и Линейку.
Тут Ножницы кликнули помощников. Пришли Циркуль и Линейка и принялись за дело.
Циркуль расставил свои ноги и измерил один отрезок, затем подошёл к другому, самому маленькому, и Совёнок сразу увидел, что этот отрезок меньше первого.
– А линейка может точно ответить, насколько этот отрезок меньше, – важно ответил Циркуль, – а я могу снова соединить отрезки.
Циркуль подтянул лучи друг к другу, соединил их концами, и вот что получилось.
– Да, – воскликнула Точка, – это не прямая. Здесь прямо не пройдёшь, придётся поворачивать. Что же это такое? Как это называется?
– Это угол, – сказал Циркуль.
– Угол… Угол… – несколько раз повторила Точка новое для неё слово -Циркуль, а как называется то место, где соединяются лучи?
– Вершина угла. Сейчас ты Точка в вершине угла. А лучи, которые начинаются от тебя, – это стороны угла. Можно даже прокатиться разок-другой. Понравился Точке такой совет. Катится она и приговаривает:
От вершины по лучу
Словно с горки покачу.
только луч теперь – «она»,
Он зовется «сторона».
Покаталась Точка ещё немного по сторонам угла, а потом вернулась к вершине и обратилась к Циркулю:
– Я хочу катиться быстрее. Нельзя ли сделать горку круче?
– Можно, – ответил Циркуль.
– Он сдвинул стороны угла.
– Это уж слишком? – запищала Точка.
– Какой острый угол? С такой крутой горки кубарем покатишься? Не нужно так круто?
Циркуль раздвинул немного стороны угла.
– Теперь хорошо, – сказала Точка. – Но мне уже расхотелось кататься. Лучше расскажи мне всё, что ты знаешь об угле.
– Углы бывают разные: прямые; углы, которые шире прямых, называются тупыми углами; а углы, которые меньше прямых, называются острыми углами.
О треугольнике
Давным-давно в математическом царстве было геометрическое Государство и правил им король Треугольникус. Был он уже старым и часто болел. Однажды собирает он своих глашатаев и посылает их по сёлам и городам с заданием: найти человека, который вылечил бы Треугольникуса. И такой лекарь нашёлся в городке «Три стороны».
Пришёл он к королю с треугольным листом, на котором был изображён чертёж и поставлен вопрос: сколько на этом чертеже различных треугольников? Назови их. Король Треугольникус думал целый день. А когда решил, почувствовал себя сразу здоровым и помолодевшим.
Но ты-то, дружок, здоров. Тебе не составит большого труда подсчитать все треугольники в этой фигуре. Но на всякий случай и ты послушай совет, который дал королю на прощание лекарь:
Кто более или менее
С терпением знаком,
Считает он терпение
Совсем не пустяком.
Не случай, не везение
Тебе помогут вдруг.
Терпение, терпение
– Твой самый лучший друг.
Да, забыли вам сообщить самое главное. Как только король сел за разгадывание количества треугольников на рисунке, послышалась музыка. Это пели треугольнички. Надеюсь, ты не забыл, что дело происходило в волшебной стране?
Если хочешь, можешь даже выучить песенку треугольничков, Она ведь волшебная и поможет тебе веселее и быстрее разгадать любую задачу:
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три.
Три стороны и три угла
И столько же вершин.
И трижды трудные дела
Мы трижды совершим.
Все в нашем городе – друзья,
Дружнее не сыскать.
Мы треугольников семья,
Нас каждый должен знать.
В. Шитомирский
01.08.2021 в 20:39. Рубрики: Стихи и рассказы. Темы: Материалы по математике в детском саду
Что такое единичный отрезок 5 класс?
– координата точки. Единичный отрезок– это расстояние от0до точки, выбранной для измерения. Отрезок – часть прямой, ограниченная с двух сторон точками.
Для чего нужен единичный отрезок?
Единичный отрезок в математике Единичный интервал, как множество чисел положительных, но не превосходящих единицы, является одним из основных множеств для построения примеров, во всех областях математики. Очень много определённых математических величин лежит на единичном отрезке.
Что такое единичный отрезок на луче?
Точка O — начало луча, и этой точке соответствует число 0. Эта точка — начало отсчёта. Точке E соответствует число 1, а длина отрезка OE принята за единицу длины и называется единичным отрезком. Число, соответствующее точке координатного луча, называется координатой этой точки.
Что такой отрезок?
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Что такое отрезок по математике?
Определение Отрезок – это часть прямой, ограниченный двумя точками. Отрезок всегда имеет определенное значение.
Что такое отрезок по геометрии?
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало, и конец. Основное свойство отрезка — это его длина. Длина отрезка — это расстояние между его концами.
Как выглядит отрезок?
Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого. Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Что такое отрезок правила по геометрии 7 класс?
Отрезок — часть прямой, ограниченная двумя точками. Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T.
Как определить отрезок?
- Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой.
- Длина отрезка — это расстояние между концами отрезка.
- Равные отрезки — это отрезки, имеющие одинаковую длину.
- Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Что такое луч прямая и отрезок?
Луч — это часть прямой, ограниченная одной точкой. Луч имеет начало, но не имеет конца. Его можно продолжить только в одну сторону. Отрезок — часть прямой, ограниченная двумя точками.
Как правильно измерить отрезок?
Для того чтобы правильно измерить длину отрезка, нужно приложить линейку нолем к началу отрезка и посмотреть, на каком делении наш отрезок заканчивается. Получается, второй конец отрезка находится на делении 10. Значит, длина отрезка 10 сантиметров. В математике сокращенно записывают ответ так: длина отрезка 10 см.
Как называется отрезок?
Отрезком называется часть прямой, ограниченная двумя точками А и В, включая эти точки (См. Точки, ограничивающие отрезок, называются его концами. Отрезок содержит точки Аи В и все точки, лежащие между ними. Обозначается отрезок АВ или ВА.
Как называется отрезок проведённый из данной точки к данной прямой Если этот отрезок и данная прямая перпендикулярны?
Перпендикуляром из данной точки к данной прямой называется отрезок, лежащий на прямой, перпендикулярной данной, которая проходит через данную точку.
Что такое отрезок в математике 2 класс?
Отрезок – это часть прямой, у которой есть начало и конец. Длина отрезка — это расстояние между его начальной и конечной точками.
Что такое луч в геометрии как обозначаются лучи?
Объединение открытого луча с его началом — точкой O — называется лучом с началом в O. Луч с началом в точке O, содержащий точку A, обозначается «луч ОА» или [OA).
Как правильно обозначается луч?
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC. Посмотрим на следующий пример: Луч с началом в точке A можно обозначить как AB или AC.
Что такое луч в математике 1 класс?
Луч – часть прямой, которая имеет начало, но не имеет конца. Обозначается, как показано на рисунке. Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами. Ломаная на рисунке обозначается A1A2A3A4A5A6 A 1 A 2 A 3 A 4 A 5 A 6 .
Что такое луч в математике?
Точка А разделила прямую на две части. Каждую из этих частей называют лучом, исходящим из точки А. Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Что такое прямая в математике 5 класс?
Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов. На рисунке изображены две прямые: CD и EF.
Что такое луч как они обозначаются?
Точка начала луча разделяет прямую на две части. Обычно луч обозначают малой латинской буквой (например, луч h), либо двумя большими латинскими буквами, первая из которых обозначает начало луча, а вторая — какую-нибудь точку на луче (например, луч АО).
Что такое луч в геометрии 7 класс?
Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.
Как сравнить два отрезка геометрия 7 класс?
Ответ: Надо наложить один отрезок на другой так, чтобы конец одного отрезка совместился с концом другого. Если при этом два других конца отрезков тоже совместились, то значит отрезки равны.
Как обозначаются лучи и углы?
1. Луч — часть прямой, которая начинается, но не заканчивается. Обозначают так: точка отсчета, начало луча, к примеру А, вторая буква — это ближе к концу графического изображения луча, к примеру В. Сами лучи называются сторонами угла, а общая точка, из которой лучи выходят, называются вершиной угла.
Что такое Что такое прямая?
Пряма́я — одно из фундаментальных понятий геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Что означает прямая линия?
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Что значит прямая линия?
Линия прямой связи местной телефонной сети (Ндп. некоммутируемая линия связи) — линия местной телефонной сети, соединяющая источник информации с её потребителем без участия коммутационных устройств телефонных станций сети.
Какие бывают виды линий?
Виды линий
- Точка. Кривая. Прямая линия.
- Отрезок. Луч
- Ломаная линия
- Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Какие бывают линии чертежа?
§ 2. Линии чертежа
- Сплошная толстая основная линия.
- Штриховая линия.
- Штрихпунктирная тонкая линия.
- Штрихпунктирная с двумя точками тонкая линия показывает линии сгиба на развертках и крайние положения подвижных предметов.
- Сплошная тонкая линия.
Какие бывают линии в рисовании?
Как видите разновидностей очень много и каждая служит своей цели. В рисунке различают ещё три основных вида — линия контура, самостоятельная линия и тонирующая линия (штрихи). Сегодня уделим особое внимание контуру. Контур — это линия, которая фиксирует очертания формы и является простейшим переходом от линии к фигуре.
Что такое незамкнутая фигура?
Итак, линия, концы которой не соединены вместе, называется незамкнутой линией. Линия, концы которой соединены вместе, называется замкнутой линией. Каждая ломаная линия состоит из нескольких отрезков – звеньев. Звенья ломаной не лежат на одной прямой.

Введение
На мой взгляд, рейкастинг — великолепная концепция, понять которую не так сложно, но качественных ресурсов по ней очень мало. Я расскажу о математике, лежащей в её основе, чтобы вы при желании с лёгкостью могли реализовать её в своих будущих проектах. Постараюсь сделать объяснение как можно более понятным, рассказать о всех тонкостях и проблемах, с которыми вы можете столкнуться. Также мы поговорим об оптимизации и о том, как сильно вам могут помочь пространственные хэш-карты. Ещё я напишу простые интерактивные примеры, с которыми вы сможете поэкспериментировать. Учтите, что демо написаны максимально простым образом, не ожидайте увидеть в них код уровня энтерпрайза — мы изучаем саму концепцию, а не реализацию.
Что такое рейкастинг?
«Рейкастинг (ray casting, „испускание лучей“) — самый простой из множества алгоритмов рендеринга компьютерной графики, использующих геометрический алгоритм трассировки лучей (ray tracing). Алгоритмы рендеринга на основе трассировки лучей работают на уровне изображений, выполняя рендеринг трёхмерных сцен в двухмерные изображения…
Принцип рейкастинга заключается в том, чтобы попиксельно отслеживать испускаемые из глаза лучи, чтобы найти ближайший объект, препятствующий пути каждого луча — представьте, что изображение — это проволочная сетка, а каждый квадрат сетки — это пиксель. Таким образом мы можем определить объект, который видит глаз через этот пиксель.» — Википедия
Ну, звучит не очень понятно, правда? Давайте упростим объяснение. Рейкастинг — это популярная фундаментальная техника, используемая для определения видимости определённых объектов (полигонов) трассировкой лучей из глаза (например, персонажа игрока) до каждого пикселя (ну, в нашем случае это не совсем так, но подробнее об этом позже) и нахождением самых ближайших пересечений с объектами.
Где может использоваться рейкастинг?
Рейкастинг можно использовать по-разному, особенно в трёхмерном пространстве. Я выделю три наиболее важных по моему мнению применения, часто встречающихся в игровых 2D-движках:
Создание 3D-перспективы на 2D-карте
Самой известной игрой, использующей эту технику, является Wolfenstein 3D. Лучи в ней трассировались для определения ближайших объектов, а их расстояние от позиции игрока использовалось для правильного масштабирования.

Простой рейкастинг с коррекцией фишай Лукаса Виейра
Задача точки в многоугольнике
Задача PIP (point-in-polygon) заключается в определении того, находится ли точка внутри, снаружи или на границе многоугольника. При помощи алгоритма рейкастинга мы можем посчитать, сколько раз точка пересекает края многоугольника. Если количество пересечений чётно, то точка находится снаружи многоугольника. Если количество пересечений нечётно, то точка находится внутри или на границе многоугольника.

Решение задачи точки в многоугольнике при помощи рейкастинга
Видимость объектов и испускание света
В статье мы рассмотрим именно эту задачу — определение видимости объектов для игрока и освещение видимой области.

Видимость объектов и испускание света
Видимость объектов и испускание света в 2D-играх
В этом разделе мы рассмотрим такие базовые понятия, как точки пересечения, испускание лучей, сортировка точек пересечения для освещения видимой области, а также несколько слов скажем о кругах. На каждом из этапов я буду писать интерактивные демо, чтобы вы не запутались и могли сразу же увидеть результаты.
Точка пересечения отрезка и луча
Здесь мы поговорим о точках пересечения. Давайте поэтапно разберёмся, как их находить и использовать. Сначала мы выведем параметрическое уравнение прямой, вычислим точки пересечения, а затем узнаем, как эффективно определять ближайшую из них.
Вывод параметрического уравнения прямой
Давайте сначала поговорим о прямых и их параметрическом уравнении.

Пример прямой линии
Мы можем выразить вектор следующим уравнением:
, где
— параметр уравнения, определяющий, насколько мы растягиваем
или сжимаем
, и меняем ли мы направление
вектора
относительно вектора
.
Позвольте продемонстрировать пару примеров:

Пример параметров параметрического уравнения прямой
Как вы могли заметить, мы можем использовать как коэффициент масштабирования:
. Мы воспользуемся этим при определении ближайшей точки пересечения.
Теперь мы можем легко увидеть, нужно ли нам, чтобы точка находилась на:
Выяснив всё это, мы наконец можем вывести параметрическое уравнение:
Если вы всё ещё не понимаете, что здесь происходит, то рекомендую вам прочитать потрясающую короткую лекцию Норма Прокупа: Parametrizing a Line Segment — Concept.
Вычисление точки пересечения
Допустим, точка является точкой пересечения отрезка прямой, заданного точками
и
, и луча, заданного точками
и
. Тогда точку
можно выразить как систему из двух уравнений:
Вычислим и
:
.
Подставим во второе уравнение:
Подставим в первое уравнение:
Вычислив и
, мы можем вычислить
при помощи одного из уравнений системы.

Демо 1 — все точки пересечения
[Прим. пер.: в оригинале статьи все демо интерактивны.]
Поиск ближайшей точки пересечения
Для правильной отрисовки видимой области нам нужна только ближайшая точка пересечения. Наивным решением было бы вычисление расстояний между точкой начала луча и точками пересечения при помощи теоремы Пифагора: . Но вы помните о параметре уравнения прямой? Я уже говорил, что мы можем использовать его как коэффициент масштабирования. Так как мы хотим сравнить расстояния на луче, то можем найти наименьшее значение параметра
:
.

Демо 2 — ближайшая точка пересечения
Испускание лучей
В этом разделе мы рассмотрим два способа испускания лучей. Мы сравним их и расскажем об их достоинствах и недостатках.
Испускание лучей по углу смещения
Первый способ — это испускание лучей во всех направлениях с заданным углом смещения. Например, мы можем испустить 30 лучей, смещённых на . Давайте сначала узнаем, как сгенерировать все эти лучи.
Пусть будет начальной точкой всех лучей, а
— некой точкой на прямой, проходящей через
под углом
:

Линия из заданной точки под неким углом
Мы можем задать как
, а
как
(наша ось Y перевёрнута, отсюда и минус).
Теперь нам нужно вывести формулы для и
:
В нашем случае — это произвольное значение больше нуля (мы ищем любую точку на прямой), поэтому для упрощения вычислений вполне можно допустить, что
. С учётом всего этого
, где
— это угловое смещение.

Демо 3 — испускание лучей на угол смещения
Испускание лучей в вершины
Вероятнее всего, вам больше подойдёт испускание лучей в вершины. Вместо испускания лучей во всех направлениях мы просто можем испускать их в вершины многоугольников. Если количество вершин невелико, мы можем сэкономить вычислительные ресурсы, не испуская бесполезные лучи. В следующих разделах мы увидим, как это влияет на плавность анимаций, а также узнаем, как оптимизировать весь процесс.

Демо 4 — испускание лучей в вершины
Освещение видимой области
Сейчас начинается самое интересное. Мы осветим видимую область заливкой огромного многоугольника.
Сортировка точек пересечения
Чтобы создать правильный порядок вершин для построения многоугольника, нужно сначала отсортировать их по углу. Для этого мы используем функцию . Подробнее о ней можно прочитать здесь.
Давайте сравним оба способа испускания лучей:

Демо 5 — испускание лучей с углами смещения (заполненная видимая область)

Демо 6 — испускание лучей в вершины (заполненная видимая область)
Оба способа выглядят ошибочными, скачущими и неточными. Давайте разберёмся, почему.
Испускание лучей с небольшим смещением
Заметьте, что происходит, когда лучи испускаются непосредственно на вершины — они должны идти дальше этой вершины, но мы получаем только ближайшую точку пересечения:

Проблема лучей на вершинах
Самым популярным решением является испускание двух дополнительных лучей со смещением на небольшой угол (в обоих направлениях) для каждого испущенного луча. Рассмотрим луч , начинающийся в
и проходящий через
. Нам нужна такая точка
, чтобы луч
был повёрнут на
с начальной точкой
.
будет иметь следующие координаты:
Обратите внимание, что для первого способа это делать не нужно — мы просто прибавляем или вычитаем смещение из угла, который вычисляем. Дополнительные объяснения можно прочитать в этой статье.

Проблема лучей в вершинах решена
Давайте посмотрим, как ведёт себя освещение после этих изменений:

Демо 7 — испускание лучей с углом смещения (заполненная видимая область с дополнительными лучами)

Демо 8 — испускание лучей в вершины (заполненная видимая область с дополнительными лучами)
В случае первого способа это не особо улучшило ситуацию. Мы можем уменьшить смещение углов (увеличив количество лучей), но результат всё равно будет плохим. С другой стороны, второй способ выглядит очень плавным и точным. Далее мы больше не будем говорить о первом способе.
Круг видимости и фонарик
Иногда нам бывает нужно ограничивать видимость для игрока. Этого можно достичь, создав область усечения нужной формы. В показанных ниже демо я использовал метод CanvasRenderingContext2D.clip().

Демо 9 — круг видимости

Демо 10 — фонарик
Как вы могли заметить, это не является оптимизацией — мы всё равно вычисляем все точки пересечения. Мы вернёмся к этому после того, как узнаем о пространственных хэш-картах.
А как насчёт окружностей?
Я редко видел случаи испускания лучей на окружности. Считайте этот раздел дополнением, в котором я вкратце о них упомяну. Я покажу уравнения и простые демо, а дальнейшую работу оставлю вам.
Точка пересечения окружности и луча
Пусть будет точкой пересечения,
— начальной точкой луча,
— точкой на луче,
— точкой центра окружности, а
— её радиусом.
Решаем относительно :
Решаем квадратное уравнение:
Только в случае :
Только в случае :
Только в случае :
Только в случае :

Демо 11 — пересечение луча и окружности
Испускание лучей на окружности
Нам нужно найти две касательные к заданной окружности, проходящие через точку начала луча.
Пусть — точки касательных,
— точка начала луча,
— центр окружности, а
— её радиус. Также мы будем перемещать все точки при помощи вектора переноса
:
так, чтобы центр окружности находился в
.
Из уравнения окружности:
Из линии перпендикуляра к радиусу окружности:
Решаем систему уравнений:
Подставляем в первое уравнение:
Решаем квадратное уравнение:
Только в случае :
Только в случае :
Но есть ещё одна проблема — это не сработает, если . Присмотримся к следующему уравнению:
. Если
, уравнение принимает следующий вид:
— больше мы не можем подставить
. Вот как решить эту систему уравнений, если такое случится:
Решаем систему уравнений:
Подставим в первое уравнение:
Решим квадратное уравнение:
Только в случае :
Только в случае :
Заметьте, что тоже самое мы можем сделать при , однако это необязательно. Если
, то решений нет.
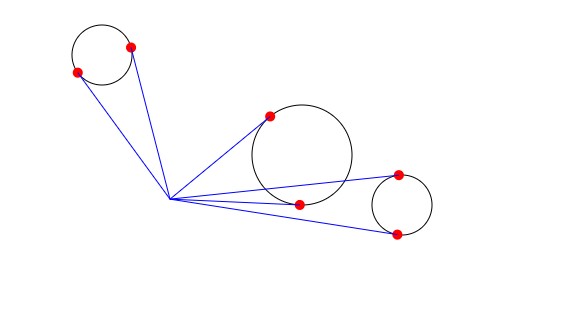
Демо 12 — испускание лучей на окружности
Способы оптимизации
В этом разделе мы поговорим об использовании пространственных хэш-карт и модифицированного алгоритма рисования линий Брезенхэма. Я не буду вдаваться в подробности реализации, потому что они широко доступны в Интернете. Однако я напишу несколько демо, чтобы вы могли их тестировать и придумывать новые идеи их применения.
Пространственные хэш-карты
Пока мы отрисовываем все многоугольники и вычисляем все точки пересечения, но это практически бесполезно. В большинстве случаев игровая область гораздо больше окна обзора. При помощи пространственных хэш-карт мы можем быстро определять, какие многоугольники видны игроку и выполнять адекватные вычисления.
По сути, мы хотим разделить игровую область на меньшие ячейки (заданного размера). Каждая ячейка состоит из списка, содержащего фигуры (чаще всего это отрезки прямых). Если одна фигура растянулась на несколько ячеек, то она будет включена во все эти ячейки.
Из названия этой методики понятно, что в ней используются хэш-карты (т.е. ячейки будут иметь названия вида X+»:»+Y), но в нашем случае желательней будет простой 2D-массив.
Вот простое демо, показывающее, как это может работать:

Демо 13 — пространственные хэш-карты
Как говорилось выше, мы можем применять их для окон обзора, а также для окружностей видимости и фонариков.
Линия сверхпокрытия на основе алгоритма Брезенхэма
При помощи пространственных хэш-карт и модифицированного алгоритма отрисовки линий Брезенхэма мы можем эффективным образом обходить сетку, выполняя минимальное количество проверок. Алгоритм должен завершать выполнение после обнаружения первой ячейки с точкой пересечения.
Подробнее об алгоритме отрисовки линий Брезенхэма можно прочитать здесь, а об его модифицированной версии — здесь.

Демо 14 — Линия сверхпокрытия на основе алгоритма Брезенхэма
Всё имеет свой конец
Простите, к сожалению, я говорю об этой статье, а не о лучах.
Думаю, мы раскрыли всё необходимое для того, чтобы вы могли приступить к работе. Если я найду что-то, требующее дальнейшего объяснения, то постараюсь дополнить статью. Кроме того, я создал небольшую шпаргалку для напоминания о некоторых темах и выведенных формулах.
Если вам понравилась статья, то поставьте звёздочку и подпишитесь на этот репозиторий на GitHub.