Сказка о натуральных чисел

Математическая сказка «Чем отличаются цифры от чисел»

Татьяна Бушенкова
Математическая сказка «Чем отличаются цифры от чисел»

Сказка «Чем отличаются цифры от чисел»

Цель: — закрепить знания о цифрах и числах;

— побуждать к выделению предметов имеющих геометрические формы.

Жил-был мальчик Вова. Он очень не любил заниматься математикой. И вот когда очередной раз прогуливал урок, прохлаждаясь в парке, катался с горки, полеживал на мягкой травке под деревом, слушал пение птиц и радовался яркому и жаркому солнцу. Вдруг внезапно солнце заволокло тучами, стало темно, поднялся сильный ветер, да все как закружит. Вова и попал в этот вихрь, и унес его далеко, далеко в математическое государство. Мальчик не сразу понял, где это он очутился. Там было так необыкновенно красиво. Красивые дома в форме геометрических фигур.

По тропинке бежит ежик, прыгает кенгуру, под кустом сидит зайчик, по стволу дерева стучит дятел, а сидя, важно на ветке наблюдает за Вовой попугай, так как он следит за порядком в государстве. В самом центре государства находится озеро большое, ну просто очень большое,- по которому даже ходят корабли, не далеко от берега сложив крылья спит утка, рядом стоит, охраняет сон цапля. Обратила внимание на чужака — Вову и смотрит с презрением, еще одна обитательница государства. А Вова все смотрит, рассматривает, диву дивится, таких интересных птиц-цифр (чисел, животных-цифр (чисел) ни где еще не встречал. Идет он дальше и дальше, вот на полянке петушок с курочкой зернышки клюют.

Долго ходил прогульщик по Математическому государства, пока не вышел на дорожку которая вела к очень яркому, сияющему замку. Вова даже ахнул от удивления и скорее побежал в замок, пока были открыты ворота. Как только он вошел, и ворота за ним захлопнулись. Он очень напугался, начал бегать, кричать, звать на помощь. В замке было тихо только эхо раздавалось от Вовочкиных криков и его ни кто не слышал. И вдруг яркий свет ослепил глаза, перед мальчиком появилась Государыня Математика – «Не плачь, расскажи мне мальчик Вова, как же ты тут оказался?» Конечно, прогульщику пришлось рассказать, как он прогулял урок математики. Математика внимательно выслушала мальчика и сказала, что может помочь ему, если только расскажет, чем цифры отличаются от чисел. А если не знает, то останется навсегда жить в замке и прислуживать ей.

Тут- то от страха прогульщик Вова и вспомнил: — «Цифра и число — это два разных понятия. Цифра обозначает обычно символ, знак. Число обозначает количество. Двухзначное число — это число, состоящее из двух цифр. Существуют различия в понятиях «цифра» и «число». Всего существует 9 цифр: 1,2,3,4,5,6,7,8,9,0. К числам относятся 1,2,3,4,5,6,7,8,9,0, а также 10,11,12 и многие другие.

Числа состоят из цифр и обозначаются ими. Число 1 состоит из цифры 1. Число 200 состоит из цифр 2 и 0. Число 25 состоит из двух цифр: 2 и 5. Номер мобильного телефона 9876543210 состоит из десяти цифр.

Цифра — это символ или графический знак, с помощью которого записывается число.

Однозначные числа можно перепутать с цифрами. Числа можно складывать, делить и проводить с ними другие математические операции. Этого нельзя делать с цифрами. Цифрами можно обозначить что-либо, например, уравнение».

Государыня Математика была очень удивлена такими знаниями прогульщика. «Ну что же, хорошо, возвращайся домой». Ворота отварились и Вова радостный побежал по дорожке и начал капать дождик. И тут то Вова и проснулся от того, что на его лицо попадали капли дождя, начал подниматься ветер. Он быстренько встал стряхнул с себя листву, траву и побежал в школу. «Неееет, я больше ни когда ни буду прогуливать уроки математики, она такая интересная и занимательная!»

Математическая сказка в познавательном развитии младших дошкольников «Математическая сказка в познавательном развитии младших дошкольников». МКДОУ – детский сад Лучик, подготовила воспитатель первой квалификационной.

Дидактическая игра «Чем питаются животные» по закреплению знаний о том, чем питаются разные домашние и дикие животные Зайка завтракал на грядке, Как же овощи здесь сладки! Уплетал зайчишка ловко И капустку, и морковку. (Людмила Громова) Ежик по лесу гулял,.

Конспект непосредственной образовательной деятельности по ФЭМП «Математическая сказка». Подготовительная группа Цель: систематизировать элементарные математические представления. Задачи: закреплять названия времен года, дней недели, закреплять элементарные.

Лэпбук «Цифры от 0 до 5» Лэпбук – это картонная папка, в которой собран материал на тему » Цифры от 0 до 5 «, которую я сделала для детей, чтобы привить своим детям.

Конспект занятия по математике в подготовительной группе «Математическая сказка «Колобок» Конспект занятия по математике в подготовительной группе. Цели: 1. Закреплять знания детей порядкового счета в пределах 10 (прямой и обратный.

Математическая сказка о точке В одном пенале жил простой карандаш. Думаете, он был самым обыкновенным? Нет, карандаш был волшебным и, поэтому всё, что он рисовал, оживало.

Математическая сказка «Сказка о том, как Петя спас волшебную страну» В одной чудесной, волшебной стране жили не обычные жители. Они никогда не ругались между собой, были очень дружелюбными. И сама страна у.

Презентация «Разностное и кратное сравнение чисел» «Решение задач на кратное и разностное сравнение чисел» Урок в 5 «в» классе коррекционной школы VIII вида Подготовила: учитель математики.

Урок математики в 6 классе «Сравнение чисел» Тема: Сравнение чисел Тип урока: «открытие» новых знаний Цель урока: формирование навыка сравнения отрицательных чисел и чисел с разными.

Занятие в подготовительной группе «В мире чисел» Занятия по математическому развитию в подготовительной группе Тема. «В мире чисел» Программное содержание: 1. Учить детей составлять задачи,.

Чем цифры отличаются от чисел: отличия и виды.

Термин «число» возникло в древние времена, когда у людей впервые получилось посчитать предметы. Первое время счёт вёлся на пальцах. Затем начали считать по зарубками на палочках. Со временем люди стали понимать числа свободно от предметов и лиц, которые могли подвергаться счёту. Поэтому у славян возникло слово «число».

В XV веке в европейских странах начали распространяться специальные знаки, с помощью которых обозначались числа (числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0). Это было изобретением индейцев, а позже они появились в Европе благодаря арабам (арабские цифры). Почему они именно такие, какие есть?

Если посмотреть внимательно на эти арабские числа, то можно заметить, что каждое число соответствует количеству углов, которое можно найти на этой цифре. У числа 0 нет углов, у числа 1 — один угол, а у 9 — все девять углов.

С середины ХVIII века у слова цифра появилось новое значение — знак числа.

В чем разница между цифрой и числом?

Итак, у слова число и цифра различное значение и происхождение. Число — единица счёта, которая выражает количество (один дом, два дома, и т.д.). Цифра — знак (символ), который обозначает значение числа. Для записи чисел используются арабские цифры — 1, 2, 3… 9, иногда и римские — I, II, III, IV, V и т.д.

В разговоре слова число и цифра заменяют друг друга. Например, под числом мы понимаем не только величину, но и знак, выражающий её.

Названия и последовательность натуральных чисел от 1 до 20

Числа 1,2,3,4,5,6,7,8,9,0, которые используются при счёте- это натуральные числа. С помощью цифр 0,1,2,3,4,5,6,7,8,9 можно записать натуральное число. Такая запись чисел называется десятичной. В каждом классе присутствует три разряда.

Приведём ниже таблицу разрядов.

Классы Миллиарды Миллионы Тысячи Единицы

Разряд Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы

1-е число 2 0 0 3 2 4 0 6 0 0 8 1

2-е число 4 7 0 0 0 0 2 0 2 3 0 0

3-е число 5 0 0 1 0 0 0 3 1 0 9 0

Вот так читаются некоторые числа:

1) десять миллиардов тридцать два миллиона четыреста шестьдесят девять тысяч восемь;
2) четыреста семьдесят миллиардов сто тридцать тысяч триста;
3) пять миллиардов три миллиона триста десять.

Существуют и такие классы: класс триллионов, класс квадриллионов, класс квинтиллионов.

Сравнение натуральных чисел

Сравнить два натуральных числа- значит установить, какое из них больше (меньше) другого. Результат сравнения записывается в виде неравенства с помощью знаков > (больше) и 253 981=2×10 6 +5×10 5 +3×10 4 +9×10 3 +8×10 2 +1×10 1

Также степень числа 10 используется и в написании десятичных дробей : 10 (-1) – это 0,1 или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n в таком случае будет обозначать положение цифры от запятой справа налево, например: 0,347629= 3×10 (-1) +4×10 (-2) +7×10 (-3) +6×10 (-4) +2×10 (-5) +9×10 (-6)

Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325 – триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5 .

Таблица названий больших чисел, разрядов и классов

1-й класс единицы	1-й разряд единицы 2-й разряд десятки 3-й разряд сотни	1 = 10 0 10 = 10 1 100 = 10 2
2-й класс тысячи	1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч	1 000 = 10 3 10 000 = 10 4 100 000 = 10 5
3-й класс миллионы	1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов	1 000 000 = 10 6 10 000 000 = 10 7 100 000 000 = 10 8
4-й класс миллиарды	1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов	1 000 000 000 = 10 9 10 000 000 000 = 10 10 100 000 000 000 = 10 11
5-й класс триллионы	1-й разряд единицы триллионов 2-й разряд десятки триллионов 3-й разряд сотни триллионов	1 000 000 000 000 = 10 12 10 000 000 000 000 = 10 13 100 000 000 000 000 = 10 14
6-й класс квадриллионы	1-й разряд единицы квадриллионов 2-й разряд десятки квадриллионов 3-й разряд десятки квадриллионов	1 000 000 000 000 000 = 10 15 10 000 000 000 000 000 = 10 16 100 000 000 000 000 000 = 10 17
7-й класс квинтиллионы	1-й разряд единицы квинтиллионов 2-й разряд десятки квинтиллионов 3-й разряд сотни квинтиллионов	1 000 000 000 000 000 000 = 10 18 10 000 000 000 000 000 000 = 10 19 100 000 000 000 000 000 000 = 10 20
8-й класс секстиллионы	1-й разряд единицы секстиллионов 2-й разряд десятки секстиллионов 3-й разряд сотни секстиллионов	1 000 000 000 000 000 000 000 = 10 21 10 000 000 000 000 000 000 000 = 10 22 1 00 000 000 000 000 000 000 000 = 10 23
9-й класс септиллионы	1-й разряд единицы септиллионов 2-й разряд десятки септиллионов 3-й разряд сотни септиллионов	1 000 000 000 000 000 000 000 000 = 10 24 10 000 000 000 000 000 000 000 000 = 10 25 100 000 000 000 000 000 000 000 000 = 10 26
10-й класс октиллион	1-й разряд единицы октиллионов 2-й разряд десятки октиллионов 3-й разряд сотни октиллионов	1 000 000 000 000 000 000 000 000 000 = 10 27 10 000 000 000 000 000 000 000 000 000 = 10 28 100 000 000 000 000 000 000 000 000 000 = 10 29

Казалось бы, все знают, что такое цифра и число. Но если поставить вопрос по-другому: «А число от цифры?» , то многие затруднятся с ответом. Для того, чтобы приступить к отличиям, следует дать точное определение этим понятиям.

Что такое цифра?

Цифра — это упорядоченная знаковая система, предназначенная для записи чисел. Цифрами считаются только те символы, которые в отдельности обозначают числа. Например, знак «-» хоть и применяется для того, чтобы записать число, но цифрой он не считается. Цифрами считается ряд от 0 до 9. Само слово «цифра» имеет арабские корни и обозначает «ноль» или «пустое место». Эти символы бывают следующих видов:

Это перечислены самые известные разновидности. В разных языках, например, в древнегреческом, для записи чисел используют буквы. Чаще всего в обиходной речи люди под словом «цифры» подразумевают числа, которыми записываются числовые данные. Следует помнить, что отрицательных, дробных и натуральных цифр не существует.

Привычная нам система исчисления основывается на цифрах арабского происхождения, которые стали известны европейцам в 13-м веке. До этого для записи чисел использовали римские графические символы. Сейчас эту разновидность можно увидеть на циферблате часов, а также в книгах.

Число — это основное математическое понятие. Его используют для:

количественной характеристики;
сравнения;
обозначения нумерации объектов.

Числа записываются цифрами и иногда при помощи символов операций в математике. Они возникли еще в первобытном обществе, когда появилась потребность в счете. Числа бывают:

натуральные — получаются при естественном счете;
целые — получаются при помощи объединения натуральных чисел;
рациональные — имеют вид дроби;
действительные;
комплексные.

Два последних вида чисел имеют важное значение для математического анализа и получаются благодаря расширению рациональных (для действительных) и действительных (для комплексных) чисел.

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
Число может быть отрицательным, дробным, в отличие от цифр.
Количество цифр всего 10, а чисел — бесконечное множество, т.к. они состоят из цифр.

Кроме различий, с математической точки зрения, существуют и лингвистические отличия. Они рассматривают, в каких случаях можно говорить «цифра», а когда — «число». Если в разговоре упоминаются официальные показатели, то уместно говорить слово «цифра». Это могут быть, например, статистические данные.

Понятие «цифры» широко распространено в нумерологии. Нумерологи используют это понятие как знак, который способен влиять на судьбу человека. Они наделяют его мистическими свойствами. Например, нумерологи уверены в том, что некоторые цифры притягивают удачу.

Число употребляют тогда, когда нужно назвать количество чего-либо, или когда речь идет о календарной дате или дне месяца. В русском языке для употребления этого понятия применяются порядковые числительные.

По сравнению с первобытными и древними обществами, у понятия «цифра» расширилась область употребления. Теперь это — не только в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами — теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Читальный зал

Наука и жизнь

Русский язык в школе

Русский язык за рубежом

Русская речь

Мир русского слова

Журнал «Грамоты.ру»

Исследования и монографии

Конкурсные публикации

Наука и жизнь

Числа и цифры

Доктор филологических наук Наталия Черникова

Статья опубликована в журнале « Наука и жизнь » (№ 4, 2010)

Понятие о числе зародилось в глубокой древности, когда человек научился считать предметы: два дерева, семь быков, пять рыб . Сначала счёт вели на пальцах. В разговорной речи мы до сих пор иногда слышим: «Дай пять!», то есть подай руку. А раньше говорили: «Дай пясть!» Пясть — это рука, а на руке пять пальцев. Когда-то слово пять имело конкретное значение — пять пальцев пясти, то есть руки.

Позднее вместо пальцев для счёта начали использовать зарубки на палочках. А когда возникла письменность, для обозначения чисел стали употреблять буквы. Например, у славян буква А означала число «один» (Б не имело числового значения), В — два, Г — три, Д — четыре, Е — пять.

Постепенно люди стали осознавать числа независимо от предметов и лиц, которые могли подвергаться счёту: просто число «два» или число «семь». В связи с этим у славян появилось слово число . В значении «счёт, величина, количество» его начали употреблять в русском языке с ХI века. Наши предки использовали слово число и для указания на дату, год. С ХIII века оно стало обозначать ещё и дань, подать.

В старину в книжном русском языке наряду со словом число имело хождение существительное чисмя , а также прилагательное чисменый . В ХVI веке появился глагол числити — «считать».

Во второй половине ХV века в европейских странах получили распространение специальные знаки, обозначающие числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Их изобрели индийцы, а в Европу они попали благодаря арабам, поэтому и получили название арабские цифры .

В нашей стране арабские цифры появились в Петровскую эпоху. В то же время в русский язык вошло слово цифра . Арабское по происхождению, оно тоже пришло к нам из европейских языков. У арабов первоначальное значение слова цифра — это нуль, пустое место. Именно в этом значении существительное цифра вошло во многие европейские языки, в том числе в русский. С середины ХVIII века слово цифра приобрело новое значение — знак числа.

Совокупность цифр в русском языке называлась цифирь (в старой орфографии цыфирь). Дети, изучавшие счёт, говорили: учу цифирь , пишу цифирь . (Вспомните учителя по фамилии Цыфиркин из комедии Дениса Ивановича Фонвизина «Недоросль», который обучал нерадивого Митрофанушку цифири , то есть арифметике.) При Петре I в России открыли цифирные школы — начальные государственные общеобразовательные учебные заведения для мальчиков. В них кроме других дисциплин детям преподавали цифирную науку — арифметику, математику.

Итак, слова число и цифра различаются и по значению и по происхождению. Число — единица счёта, выражающая количество ( один дом, два дома, три дома и т.д.). Цифра — знак (символ), обозначающий значение числа. Для записи чисел мы используем арабские цифры — 1, 2, 3… 9, 0, а в некоторых случаях и римские — I, II, III, IV, V и т.д.

В наши дни слова число и цифра употребляются и в других значениях. Например, когда мы спрашиваем «Какое сегодня число?», то имеем в виду день месяца. Сочетания « в том числе », « из числа кого-нибудь», « в числе кого-то» обозначают состав, совокупность людей или предметов. А если мы доказываем что-то с цифрами в руках , то обязательно используем числовые показатели. Словом цифра называют также денежную сумму ( цифра дохода, цифра гонорара ).

В разговорной речи слова число и цифра часто заменяют друг друга. Например, числом мы называем не только величину, но и знак, который её выражает. Об очень больших в числовом отношении величинах говорят астрономические числа или астрономические цифры .

Слово количество появилось в русском языке в XI веке. Оно пришло из старославянского языка и образовано от слова колико — «сколько». Существительное количество употребляется в применении ко всему, что поддаётся счёту и измерению. Это могут быть люди или предметы ( количество гостей, количество книг ), а также количество вещества, которое мы не считаем, а измеряем ( количество воды, количество песка ).

Текущий рейтинг:

Чем отличается число от цифры: математические и лингвистические различия

Казалось бы, все знают, что такое цифра и число. Но если поставить вопрос по-другому: «А чем отличается число от цифры?» , то многие затруднятся с ответом. Для того, чтобы приступить к отличиям, следует дать точное определение этим понятиям.

Что такое цифра?

арабские;
римские;
шестнадцатеричные и др.

Что такое число?

Число — это основное математическое понятие. Его используют для:

количественной характеристики;
сравнения;
обозначения нумерации объектов.

натуральные — получаются при естественном счете;
целые — получаются при помощи объединения натуральных чисел;
рациональные — имеют вид дроби;
действительные;
комплексные.

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

Отличия числа от цифры

С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
Число может быть отрицательным, дробным, в отличие от цифр.
Количество цифр всего 10, а чисел — бесконечное множество, т.к. они состоят из цифр.

По сравнению с первобытными и древними обществами, у понятия «цифра» расширилась область употребления. Теперь это — не только символ в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами — теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Чем отличается цифра от числа? Определение цифры и числа

Те символы, которыми мы сейчас пользуемся для обозначения числа, придумали умные и находчивые жители Индии более 15 веков назад. Наши предки узнали о них от арабов, которые начали их использовать раньше других.

Чем отличается цифра от числа? Цифра происходит от арабского языка и имеет прямое значение «ноль» или «пустое место». Всего насчитывается 10 цифр, которые, в свою очередь, комбинируясь разными способами, составляют числа.

Различие цифры и числа

Для того чтобы понять, каково отличие между понятиями «число» и «цифра», нужно запомнить следующие постулаты:

Цифр всего десять: ноль, один, два, три, четыре, пять, шесть, семь, восемь, девять. Все остальные их комбинации – это числа.
Цифра – это составная часть числа. Сколько цифр в числе? Их может быть разное количество.
Каждая цифра – это знак, символ. Любое число – это количественная абстракция.

Арабская «сифра»

Цифра как слово имеет арабские корни.

Изначально на арабском это было слово «сифра», т. е. «ноль». Цифры представляют собой некие символы, которыми обозначаются числа. Цифры обозначаются следующим образом:

0 — ноль;
1 — один;
2 — два;
3 — три;
4 — четыре;
5 — пять;
6 — шесть;
7 — семь;
8 — восемь;
9 — девять.

Вышеперечисленные цифры называются арабскими.

Римская система счисления

Арабская система счисления в мире не одна. Существуют и другие системы. Каждая из них совершенно не похожа на другую.

К примеру, кроме арабской системы, очень популярна римская система счета. Но римские цифры пишутся иначе и ничем не напоминают арабские.

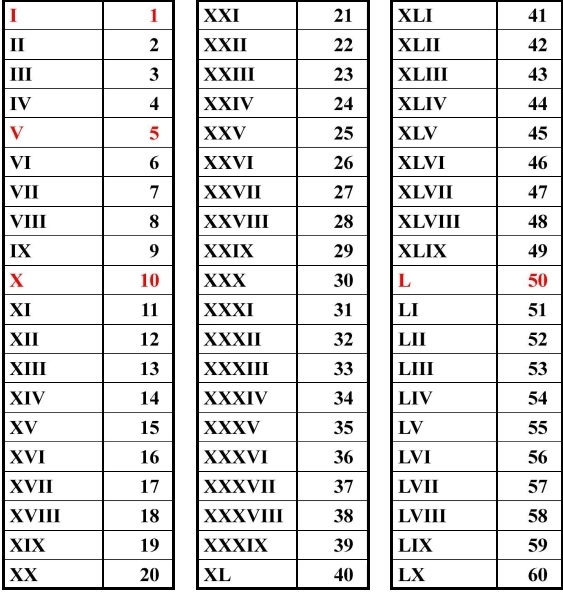
I — один;
II- два;
III — три;
IV — четыре;
V- пять;
VI- шесть;
VII — семь;
VIII — восемь;
IX — девять;
X — десять.

Как вы могли заметить, тут нет символа, обозначающего ноль. Так что в качестве цифры можно принять десятку.

Системы счисления

Система счисления – это некий вариант представления чисел.

К примеру, представьте, что перед вами лежит несколько яблок. Вы хотели бы узнать, сколько яблок лежат на столе? Для этого вы могли бы считать, загибая пальцы рук или делать зарубки на дереве. А могли бы вы и представить, что десять яблок – это одна корзинка, а одно яблоко – это одна спичка. Спички по ходу счета выкладывать на столе под одной.

В первом варианте подсчета число получилось в виде строки из зарубок на дереве (или загнутых пальцев рук), а во втором варианте подсчета – это был набор из корзинок и спичек. Слева должны быть емкости, а справа — спички.

Системы счисления бывают двух видов:

Позиционные.
Непозиционные.

Позиционные системы счисления бывают:

Однородными.
Смешанными.

Непозиционной называют такую систему счисления, в которой цифра в числе соотносится с такой величиной, которая не зависит от ее разряда. Поэтому, если у вас пять зарубок, то число будет равно пяти. Ибо каждой зарубке будет соответствовать одно яблоко.

Позиционной системой счисления является та, в которой цифра в числе будет зависеть от ее разряда.

Та система счисления, к которой мы привыкли – это десятичная система счета. Она позиционная.

Когда наши предки начали учиться считать, у них появилась идея записывать числа. изначально они использовали те самые зарубки на деревьях или камнях, где каждая черточка обозначала какой-либо предмет (одно яблоко, к примеру). Именно так и была изобретена единичная система счисления.

Единичная система счисления

Различие между цифрой и числом в единичной системе счисления в том, что число в этом случае равнозначно строке, состоящей из палочек. Количество палочек (зарубок на дереве) равняется значению числа.

К примеру, урожай из 50 яблок будет равен числу, состоящему из 50 палочек (черточек, зарубок).

Сколько цифр содержит число 50? Две цифры. Цифра 0 и цифра 5. Но количество яблок гораздо больше двух.

Основное неудобство в этой системе счисления – слишком длинная строка из черточек. А если бы урожай составлял 5 000 яблок? Действительно, записывать такое число неудобно. Прочтение тоже будет вызывать затруднения.

Поэтому позже наши предки научились группировать черточки по несколько штук (по 5, 10). И для каждой объединяющей группы был придуман специальный знак. Сначала для 5 и 10 использовали пальцы рук. А затем были придуманы определенные символы. Таким способом считать яблоки стало гораздо проще.

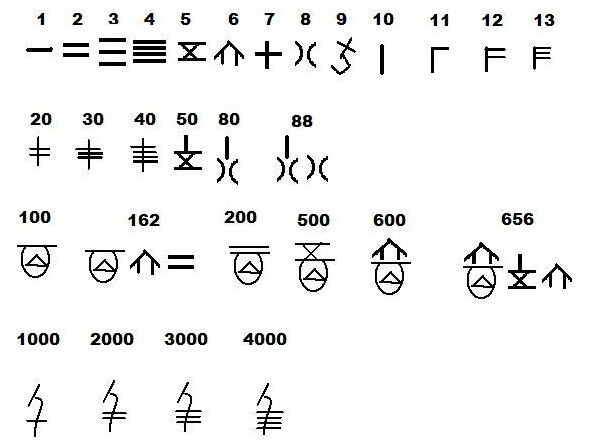
Древнеегипетская десятичная система счисления

Древние египтяне для того, чтобы обозначить числа, стали использовать специальные символы. Даже древние люди понимали, чем отличается цифра от числа.

1, 10, 10 2 , 10 3 , 10 4 , 10 5 , 10 6 , 10 7 .

Итак, предки научились группировать различные знаки (символы). Египтяне избрали для своей группировки число десять, не изменяя цифру один.

В этом конкретном примере число десять – это основание десятичной системы счисления. А каждый знак в этой системе счисления – это число 10 в какой-либо степени.

Египтяне записывали числа, комбинируя эти знаки (символы). Если число не являлось степенью десяти, все недостающие знаки добавлялись путем повторения. Каждый символ мог повториться не больше девяти раз. Итог был равен сумме элементов числа.

Двоичная система счисления

Данная система счисления в настоящее время используется в вычислительной технике. Десятичная система счисления неудобна для тех машин, которые служат людям сегодня.

Двоичная система счисления использует всего две цифры:

Ноль – 0.
Один – 1.

В каждом разряде допустима только одна цифра — либо 0, либо 1. Чтобы перевести число из двоичной в десятичную систему счисления, нужно будет умножить все цифры по очереди на основание 2, которое возводят в степень, равную разряду.

Восьмеричная система счисления

Восьмеричная система счисления тоже часто применима в современной электронике. Как вы понимаете, тут применяют всего восемь цифр.

0 – ноль;
1 – один;
2 – два;
3 – три;
4 – четыре;
5 – пять;
6 – шесть;
7 – семь.

Чтобы перевести число в десятичную систему счисления, нужно каждый разряд данного числа умножать на 8 (в степени разряда числа)_.

Шестнадцатеричные цифры

Программисты и люди, профессия которых тесно связана с компьютерными машинами, используют шестнадцатеричную систему счисления.

0 – 0;
1 – 1;
2 – 2;
3 – 3;
4 – 4;
5 – 5;
6 – 6;
7 – 7;
8 – 8;
9 – 9;
A – 10;
B – 11;
C – 12;
D – 13;
E – 14;
F – 15.

Цифра и число

Число — это понятие, которое обозначает количество.

Цифра — это символ или знак, который обозначает число.

Количество цифр в числе может быть разным, от одного до бесконечности.

К примеру, дано число «семь», которое отражает количество чего-либо. Но это самое число мы записываем цифрой 7.

Определение цифры и числа на простом языке приведем ниже.

Числа необходимы для того, чтобы вести счет каких-либо предметов, замерять длину, измерять время, скорость и другие величины. А цифра — это такой символ, который показывает число визуально, понятно и наглядно.

Грубо говоря, цифру можно сравнить с буквой из алфавита, а слово — с числом. То есть существует всего 33 знака (символа) в русском языке для обозначения букв. С их помощью можно записать сколько угодно слов. И существует всего десять цифр для обозначения чисел.

Давайте наглядно разберем, чем отличается цифра от числа.

Для того чтобы написать число 587, мы будем использовать три цифры: 5, 8 и 7. Сами по себе цифры никак не могут отразить целое число. Этими же цифрами мы можем записать еще много разных чисел. К примеру 857, 875 878755 и так далее.

Когда правильно употреблять «число», а когда — «цифра»?

Если человек скажет: «Запишите, пожалуйста, число 7. А теперь прибавьте к нему 8». Этот вариант будет считаться грамотным и правильным.

Если вам скажут: «Запишите цифру 9. И отнимите 3», это неправильно и безграмотно. От цифры никак нельзя что-то отнять. Точно так же, как от буквы, например. Это же всего лишь символ, как от него можно вычесть какое-то количество? Правильно будет: «Запишите число 9…».

Вариант «Запишите цифру 23» также некорректен. Такой цифры просто не существует. Есть число 23, которое можно записать цифрами 2 и 3.

Какая разница ?

Итак, без счета мы свою жизнь не представим. Это бесспорно. В нашем мире уже никак не прожить без цифр и чисел. Но мы крайне редко думаем о том, с чем мы сейчас имеем дело – с цифрой или все-таки с числом.

Как мы уже выяснили ранее, цифра – это просто некий символ, знак, который принято использовать для того, чтобы что-то обозначить.

Число же показывает количество чего-либо с помощью этих самых знаков – цифр.

Цифра может быть не только составной частью числа, но и числом, точнее, его аналогом. Конечно, при условии, что она обозначает количество предметов до 9 включительно.

Главные выводы

Итак, чем же отличается цифра от числа:

Цифры – это некая единица счета от нуля до девяти включительно. Все остальные комбинации цифр –это числа.
Сколько цифр в числе, обозначающем одно и то же количество, зависит от системы счисления.
Каждое число создается из цифр.
Основное различие цифры и числа в том, что первое понятие абстрактно, это всего лишь символ, а второе выражает количество чего-либо.
Число и цифра разнятся в зависимости от системы счисления. Одна и та же цифра может обозначать разное число.

Источник

87cyugr

В последнее время я думал о числе 60.

Вавилонские счетоводы и землемеры основывали свою арифметику на шестидесятеричном счислении, возможно потому, что эта система помогает в работе с дробями. Если упорядочить объекты в группы по 60, их можно делить на половины, на трети, четверти, пятые, шестые, десятые, двенадцатые, пятнадцатые, двадцатые, тридцатые и шестидесятые части. Ни одно меньшее число не имеет такого количества делителей, и благодаря этому число 60 относится к элитному классу высокосоставных чисел (этот термин и его определение были предложены в 1915 году Сринивасой Рамануджаном.)

Но у числа 60 есть и другая особенность, которую я заметил только несколько недель назад, хотя о ней могли знать вавилоняне, а уж Рамануджан знал точно. Число 60 с его выдающимся количеством делителей тесно расположено между двумя другими числами, вовсе не имеющими делителей, за исключением 1 и самого себя: и 59, и 61 являются простыми. Такие пары простых чисел, разделённые одним промежуточным целым, называются числами-близнецами. Примерами таких чисел являются пары (5, 7), (29, 31) и (1949, 1951). На протяжении многих лет исследователи теории чисел внимательно изучали числа-близнецы. Меньшего внимания удостоилось число посередине — непрошенный гость, отделяющий близнецов друг от друга. Рискуя выглядеть немного слащавым, я назову это число посередине братом близнецов, или просто братом.

Является ли случайностью то, что число, находящееся между двумя простыми, настолько непростое? Действительно ли 60 необычно в этом отношении, или существует некий паттерн, общий для всех чисел-близнецов и их братьев? Можно представить, что существует какой-то принцип справедливости: если число $inline$ окружено с двух сторон бедными на делители соседями, оно должно иметь множество делителей, чтобы скомпенсировать, уравновесить ситуацию. Возможно, каждая пара чисел-близнецов образует сэндвич с курицей и салатом, состоящий из двух ломтей простого хлеба, между которыми сжата мягкая начинка, нарубленная на множество мелких кусков.

Чтобы быстро проверить эту гипотезу, давайте составим график количества делителей $inline$ для каждого целого числа в интервале от $inline$ до $inline$ :

Рисунок 1

На Рисунке 1 числа-близнецы отмечены голубыми точками, а их братья — тёмно-синими. Высокосоставные числа ( $inline$ , которые имеют больше делителей, чем любое меньшее $inline$ ) выделены жёлтым контуром. [Обратите внимание, что 1 и 2 отмечены как высокосоставные числа, хотя они вообще не составные. Поди их разбери.]

График даёт нам понять, что многие братья близнецов (4, 6, 12 и 60) и в самом деле являются высокосоставными числами-рекордсменами, однако другие братья ими не являются (18, 30, 42 и 72). А некоторые высокосоставные числа (24, 36, 48) не расположены между числами-близнецами. Как бы то ни было, тёмно-синие точки расположены ближе к верхнему краю графика, оставляя чёткое впечатление, что братья близнецов склонны иметь множество делителей, больше, чем типичное целое число того же размера.

Интервал 1–75 является очень небольшой выборкой натуральных чисел, к тому же он достаточно необычен, поскольку чисел-близнецов много среди небольших целых, но дальше вдоль числовой оси они становятся достаточно редкими. Чтобы взглянуть на тему шире, рассмотрим количество делителей для всех положительных целых чисел до $inline$ . [Чемпионом по делимости среди этих чисел является $inline$ , имеющее 768 делителей. Оно не является братом.]

Среднее значение $inline$ на этом интервале равно 18,5751. Но если рассмотреть только братьев (а их на этом интервале 440312), то среднее количество делителей становится больше почти в три раза: 51,5889. Числа, имеющие единственного простого соседа (или $inline$ , или $inline$ , но не оба сразу), тоже имеют высокое среднее $inline$ : 32,1199.

На Рисунке 2 представлен график $inline$ для того же интервала; на нём последовательность из 100 миллионов чисел разбита на 500 блоков размером по 200000, и взято среднее значение $inline$ для каждого блока.

Рисунок 2

Взглянув на график, мы можем с уверенностью сказать, что числа, находящиеся рядом с простыми, имеют в среднем намного больше делителей, чем числа без простых соседей. Похоже на то, как будто простые числа перебрасывают все свои делители через забор во двор соседа. Или, возможно, в этом виноваты братья близнецов, по-вампирски высасывающие все делители их соседних простых.

Однако позвольте мне предложить менее изысканное объяснение. Все простые числа (за одним известным исключением) являются нечётными, то есть все ближайшие соседи простых чисел (опять-таки, за одним исключением) являются чётными. Иными словами, соседи простых чисел имеют делитель 2, что даёт им мгновенное преимущество в гонке по накоплению делителей. Соседи близнецов имеют и ещё одно преимущество: все они (за одним исключением) делимы и на 3, и на 2. Почему? Среди трёх последовательных чисел одно должно быть кратным 3, и это не может быть один из близнецов, следовательно, это их брат.

Делимость на 2 и 3 означает также делимость брата на 6. Любые другие простые делители брата умножаются на 2 и 3, создавая ещё больше делителей. Например, число, делящееся на 2, 3 и 5, также делится на 10, 15 и 30.

Рисунок 3

Учитывая этот мультипликативный эффект, кажется возможным, что делимости на 2 и 3 достаточно для объяснения выделяющегося на фоне остальных избытка делителей. Согласно этой гипотезе, близость простых чисел никак с этим не связана; братья богаты делителями просто потому, что являются кратными 6. Рисунок 3 подтверждает эту мысль. Для $inline$ , целые числа, остаток от деления на 6 которых равен нулю, имеют в два раза больше делителей, чем любой другой класс. (Простые числа находятся в классах 1 и 5.)

Однако более внимательное изучение Рисунка 3 даёт нам основание для опасений. На графике среднее значение $inline$ для делимых на 6 чисел примерно равно 43, но мы уже знаем, что для братьев (подмножества делимых на 6 чисел, расположенных между числами-близнецами) $inline$ больше 51. Это наблюдение даёт нам понять, что в конечном итоге простые числа по соседству всё-таки имеют определённое влияние на избыток делителей.

Дополнительные доказательства можно получить из ещё одного графика $inline$ для чисел с простыми соседями и без них, но на этот раз ограниченного числами, делимыми на 6. Следовательно, все элементы популяции выборки имеют одинаковое преимущество. На Рисунке 4 показаны результаты этого эксперимента.

Рисунок 4

Если бы простые соседи не оказывали влияния (кроме гарантий делимости на 6), то синяя, зелёная и красная кривые имели бы одну траекторию, но это не так. Хотя отрыв братьев в гонке делителей немного уменьшился, он не пропал полностью. Числа с двумя простыми соседями имеют примерно на 20% больше делителей, чем общее среднее для чисел, делящихся на 6. Числа с одним простым соседом тоже немного выше среднего. Следовательно, делители 2 и 3 не могут объяснить всё.

Вот простая попытка объяснения того, в чём может быть дело: аналогично тому, что любые три последовательные числа должны включать в себя одно, кратное 3, любые пять последовательных чисел должны включать в себя число, кратное 5. Если выбрать $inline$ случайно, то мы можем быть уверены, что ровно один элемент множеста $inline$ делится на 5. Так как $inline$ выбирается случайно, все элементы множества с равной вероятностью могут брать на себя эту роль, поэтому можно сказать, что 5 является делителем $inline$ с вероятностью 1/5.

Но предположим, что $inline$ является братом близнецов. Тогда $inline$ и $inline$ являются простыми, и ни одно из них не может быть кратным 5. Следовательно, нам нужно перераспределить вероятность на три оставшихся элемента множества. Похоже, теперь $inline$ кратно 5 с вероятностью 1/3. Подобные рассуждения можно применить к делимости на 7, на 11 или на любое другое простое число. В каждом из случаев вероятность увеличивается наличием соседних простых чисел.

То же рассуждение работает и в случае, если его перевернуть. Знание того, что $inline$ чётно, даёт нам понять, что $inline$ и $inline$ нечётны. Если $inline$ также кратно 3, мы знаем, что $inline$ и $inline$ не кратны 3. Аналогично с 5, 7, и так далее. Следовательно, нахождение избытка делителей $inline$ повышает вероятность того, что соседи $inline$ являются простыми.

Логична ли эта схема? У нас есть вполне обоснованные причины для сомнений. Вероятность никак не связана с распределением делителей среди целых чисел. Определяющий делимость процесс заключается в простом подсчёте, и в нём нет ничего случайного. Представьте, что вы раздаёте карты игрокам, сидящим за очень длинным столом, и их стулья пронумерованы от 1 до бесконечности. Сначала вы раздаёте каждому из игроков карту 1. Затем, начиная с игрока 2, вы раздаёте каждому второму игроку карту 2. Затем карту 3 игроку 3 и каждому третьему игроку после него, и так далее. Когда вы закончите (если вы закончите!), каждый игрок будет держать карты, соответствующие всем делителям числа на его стуле, и никаких других карт.

Эта процедура раздачи карт кажется мне логичным объяснением того, как устроены целые числа. Добавление вероятностного элемента коренным образом изменяет алгоритм. Так как мы раздаём делители, время от времени игрок отказывается брать карту, говоря «Извините, но я простое число, пожалуйста, передайте её одному из моих соседей». Затем вы случайным образом выбираете из множества соседей получателя, находящегося в подходящем интервале.

Построение числовой системы случайной раздачей делителей подобно лотерейным билетам может быть приятным развлечением, но оно не даст нам те числа, которые мы знаем и любим. Простые числа не отказывают раздающему делители; напротив, простое число является простым, потому что ни одна из карт от 1 до $inline$ не попадает на его место. И числа, делящиеся на 5, не разбросаны по числовой прямой в соответствии с каким-то локальным распределением вероятности; они встречаются с абсолютным постоянством на каждой пятой позиции. Добавление вероятности в этот контекст кажется запутывающим и бесполезным.

Но тем не менее… Тем не менее! Оно работает.

Рисунок 5

На Рисунке 5 показана доля всех $inline$ , делимых на 5, классифицированных согласно количеству близких к $inline$ простых чисел. Общее среднее равно 1/5, как и должно быть. Но среди братьев с двумя простыми соседями доля близка к 1/3, как и предсказывает вероятностная модель. И примерно 1/4 чисел с одним простым соседом является кратным 5, что опять-таки соответствует прогнозам вероятностной модели. И обратите внимание, что значения $inline$ без простых соседей имеют меньшую, чем средняя доля кратных 5. В каком-то смысле этот факт не удивляет и даже неизбежен: если среднее постоянно, и одна подгруппа имеет избыток, то дополнение к этой подгруппе должно иметь дефицит. Тем не менее, это кажется странным. Как может отсутствие простых соседей опускать плотность делящихся на 5 чисел ниже общего среднего? В конце концов, мы знаем, что кратные 5 числа неизменно становятся каждым пятым целым числом.

Рассказывая о подобных причудах братьев, я не хочу сказать, что в теории чисел есть какой-то глубокий изъян или парадокс. Фундамент арифметики не трескается из-за того, что я встретил больше ожиданного количества пятёрок в богатых простыми числами сегментах числовой прямой. Никакие числа не удалились со своих мест в последовательности целых чисел; нам не нужно их выслеживать и возвращать на нужные позиции. Изменения требует только моё понимание их распределения. Иными словами, вопрос не столько в том, что происходит, сколько в том, как правильно это воспринимать.

Я знаю множество неверных способов. Мысль о том, что числа-близнецы отпугивают делители, а братья привлекают их — это просто сказка вроде истории о крокодиле, вытянувшем нос слонёнка. Её можно принять в качестве метафоры, но не как механизм. Между целыми числами не действуют никакие силовые поля. Числа не могут ощущать свойств своих соседей. Не имеют они и индивидуальности; они не жадны и не расточительны, не общительны и не замкнуты.

Вероятностная формулировка кажется более подходящей, чем наша сказка, тем, что позволяет избежать явного упоминания причинных связей между числами. Но эта мысль всё равно таится под её поверхностью. Что значит выражение «Присутствие простых соседей увеличивает шансы числа делиться на 5»? Уж точно не то, что простое число каким-то образом влияет на результат броска монеты или вращение колеса рулетки. Это заявление имеет смысл только как эмпирическое, статистическое наблюдение: при исследовании большого количества целых чисел выяснено, что те из них, которые находятся ближе к простым числам, имеют делитель 5 чаще, чем те, которые находятся дальше. Это утверждение истинно, но оно не говорит нам, почему оно истинно. (И нет гарантии, что это наблюдение истинно для всех чисел.)

Вероятностные рассуждения не новы в теории чисел. В 1936 году Харальд Крамер писал:

Что касается порядковых простых чисел, то хорошо известно, что, грубо говоря, мы можем оценить вероятность того, что целое число $inline$ должно быть простым, приблизительно как $inline$ .

Крамер даже построил целую вероятностную модель простых чисел, проигнорировав все вопросы о делимости и просто объявив каждое целое число простым или составным на основании броска монеты (с перекосом в соответствии с вероятностью $inline$ ). В некоторых аспектах эта модель работала потрясающе. Как показано на Рисунке 6, она не только соответствует общей тенденции распределения простых чисел, но и даёт достаточно хорошую оценку распространённости чисел-близнецов.

Рисунок 6

Однако в случайной модели Крамера отсутствует намного большее. В частности, в ней совершенно упущены необычные свойства братьев чисел-близнецов. В области числовой прямой, показанной на Рисунке 6, от 1 до $inline$ , истинные братья имеют в среднем 44 делителя. Братья Крамера являются просто случайной выборкой порядковых целых чисел, имеющей в среднем 16 делителей.

По существу, распределение братьев нераздельно связано с распределением чисел-близнецов. Одних не может быть без других. Этот вывод бесполезен, ведь распределение простых чисел (как близнецов, так и не близнецов) — одна из глубочайших загадок современной математики.

В своих рассуждениях я охарактеризовал уникальные свойства братьев, подсчитывая их делители. Существуют и другие способы подхода к этой задаче, дающие схожие результаты. Например, можно вычислить сумму делителей $inline$ вместо количества $inline$ . Это приведёт нас к классическим понятиям избыточных, совершенных и недостаточных чисел. Число $inline$ избыточно, если $inline$ , идеально, если $inline$ , и недостаточно, если $inline$ . Когда я написал программу для сортировки братьев на эти три категории, то с удивлением обнаружил, что за исключением 4 и 6 каждый брат близнецов является избыточным числом. Такой характерный результат показался мне примечательным и важным. Но потом я узнал, что каждое число, делимое на 6, кроме самой шестёрки, является избыточным.

Ещё один подход заключается в подсчёте простых множителей $inline$ , а не делителей. Эти две величины имеют сильную корреляцию, хотя и количество делителей не является просто функцией от количества множителей; она также зависит от делимости множителей.

Рисунок 7

Как видно из Рисунка 7, подсчёт простых множителей рассказывает нам историю, похожую на историю подсчёта делителей. Типичное целое число в интервале до $inline$ имеет около четырёх простых множителей, а типичный брат в том же интервале — больше шести.

Также мы можем рассмотреть размер самого большого простого множителя $inline$ ( $f_{max}(n)$ ), который связан с концепцией гладкого числа. Число является гладким, если все его простые множители меньше какой-то заданной границы, которая может быть фиксированной константой или функцией от $inline$ , например $inline$ . Одним из показателей гладкости является $log n, / log f_{max}(n)$ . Вычисления показывают, что по этому определению братья более гладкие, чем среднее: соотношение логарифмов примерно равно 2,0 для братьев и примерно 1,7 для всех чисел.

Ещё один посторонний факт: ни один брат, за исключением 4, не является полным квадратом. Доказательство: предположим, что $inline$ — брат. Тогда $inline$ , а это число имеет множители $inline$ и $inline$ , то есть не может быть простым. Обобщив это рассуждение, мы исключим из списка возможных братьев кубы и все полные степени более высокого порядка.

Когда я впервые начал разбираться с братьями, то стал изучать, что по этой теме могли сказать другие люди. Я не нашёл особо много информации. Хотя объём литературы по числам-близнецам огромен, в ней рассматриваются сами простые числа, и особенно вопрос о существовании бесконечного количества близнецов — гипотеза, остававшаяся недоказанной в течение 170 лет. В этих трудах редко упоминаются числа, зажатые в сэндвиче между двумя простыми числами.

У многих разновидностей высокосоставных чисел также есть восторженные клубы фанатов, но я почти не нашёл обсуждений их частого нахождения по соседству с простыми числами.

Может ли быть так, что я первым заметил любопытные свойства братьев чисел-близнецов? Нет. Я уже давно вышел из возраста подобных забавных мечтаний. Если я не обнаружил никаких ссылок, то это без сомнения указывает на то, что я ищу не там.

В конечном итоге я нашёл несколько интересных статей и писем. Неудивительно, что ключом к их обнаружению была Онлайн-энциклопедия целочисленных последовательностей (OEIS), которая, похоже, всё больше начинает функционировать как Индексный указатель математики. Сначала я обратился к нему, но в статье о последовательностях братьев, названной «Среднее пар чисел-близнецов» имелась только одна ссылка, и она явно не была обильным источником просвещения. Она привела меня к тому журнала Eureka за 1967 год, выпускаемого кембриджским математическим сообществом The Archimedians. Всё, что я там нашёл (на странице 16) — это очень краткая задача, в которой нужно было продолжить последовательность 4, 6, 12, 18, 30, 42,…

На этом дело на несколько недель приостановилось, но позже я вернулся к OEIS, чтобы изучить перекрёстные ссылки на другие похожие последовательности. В разделе высокосоставных чисел я нашёл ссылку на статью Бенни Лима Prime Numbers Generated From Highly Composite Numbers (Parabola, 2018 год). Лим изучил соседей первой тысячи высокосоставных чисел. В верхней части интервала числа очень велики ( $10^{76}$ ), а простые числа крайне редки, но, как выяснил Лим, они не так редки среди ближайших соседей высокосоставных чисел.

Ещё одна перекрёстная ссылка привела меня к последовательности A002822, помеченной как «Числа $inline$ , такие, что $inline$ , $inline$ являются числами-близнецами». Другими словами, это множество чисел, которые при умножении на 6 дают братьев чисел-близнецов. Вот несколько первых членов последовательности: 1, 2, 3, 5, 7, 10, 12, 17, 18, 23, 25, 30, 32, 33, 38. Статья в OEIS содержит ссылку на статью 2011 года Франчески Балестриери, в которой предлагается интригующая идея, но усвоить её полностью мне пока не удалось. Балестриери показала, что $inline$ является составным, если $inline$ можно выразить как $inline$ для неких целочисленных $inline$ и $inline$ ; в противном случае оно является простым. Существует и похожее, но чуть более сложное правило для $inline$ . Далее она доказывает следующую теорему:

Гипотеза о числах-близнецах истинна тогда и только тогда, когда существует бесконечное множество $inline$ , таких, что $inline$ и $inline$ и $inline$ для всех $inline$ .

Другие цитаты вывели меня на три статьи Антони Динкулеску, датированные 2012-2018 годами, в которых исследуются близкие темы. Но самыми впечатляющими документами стали два письма, написанные Нилу Слоуну, основателю и главной движущей силе OEIS. В 1984 году достопочтенный Соломон Голомб написал ему, чтобы сообщить о множестве публикаций 1950-х и 60-х, в которых упоминается связь между $inline$ и числами-близнецами. Самым первым из таких упоминаний стала задача в American Mathematical Monthly, предложенная и решённая самим Голомбом. Когда он совершил это открытие, ему было 17 лет, и это была его первая математическая публикация. Чтобы подтвердить своё заявление о первенстве, он предложил награду в 100 долларов тому, кто сможет найти более раннюю литературу.

Во втором письме Мэттью Майерс из Спрюс-пайн (Северная Каролина) представил два таких более ранних материала. Первый — это хорошо известная история теории чисел Л. Диксона, опубликованная в 1919 году. Второй — это Essai sur les nombres premiers Вольфганга Людвига Крафта, коллеги Эйлера по Академии наук в Санкт-Петербурге. Эссе было прочитано академии в 1798 году и опубликовано в 12-м томе Nova Acta Academiae Scientiarum Imperialis Petropolitanae. В ней подробно раскрывается тема $inline$ . Эссе было выпущено за пятьдесят лет до появления понятия чисел-близнецов, а гипотеза об их бесконечности была предложена Альфонсом де Полиньяком.

Майерс сообщил об этих археологических находках в 2018 году. К сожалению, Голомб скончался двумя годами ранее.

Источник

Учебник:
Математика. 5 класс. Мерзляк А.Г. и др. (М.: Вентана — Граф,
2019)

Тип урока
– урок открытия новых знаний и их первичное закрепление.

Технологическая карта урока составлена с
учетом требований ФГОС ООО.

Дата урока
19 ноября 2020.

·
Обучающие: совершенствование
навыка умножения натуральных чисел, применение рациональных приёмов вычислений.
Продолжить работу над текстовыми задачами.

·
Развивающие: развивать
умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание,
развивать устную речь.

·
Воспитательные: воспитывать
умение высказывать свою точку зрения, слушать ответы других, принимать участие
в диалоге, формировать способность к позитивному сотрудничеству.

Личностные: умножают натуральные числа,
используют свойства умножения, применяют рациональные приёмы для вычислений,
формируют внимательность и аккуратность в вычислениях требовательное отношение
к себе и к своей работе.

Познавательные:
закрепляют навыки и умения применять алгоритмы при решении задач на умножение
натуральных чисел и применение свойств умножения, систематизируют знания,
обобщают и углубляют знания при решении задач по теме «Умножение натуральных
чисел. Переместительное свойство умножения», выбирают и формулируют
познавательную цель, выражают смысл ситуации с помощью различных примеров.

Предметные: уметь в процессе реальной ситуации
применять понятие умножение натуральных чисел и свойства умножения.

1. Самостоятельно
формулируют познавательную цель и строят свои действия в соответствии с ней.

2. Планируют
собственную деятельность, определяют средства для её осуществления.

Коммуникативные:
регулируют собственную деятельность посредством речевых действий, умение
слушать и вступать в диалог, воспитывать чувство взаимопомощи. Уважительное
отношение к чужому умению, культуру учебного труда, требовательное отношение к
себе и своей работе.

Оборудование:
доска, задания для выполнения на уроке, проектор, задания для домашней работы, презентация.

Тема урока

Умножение. Переместительное свойство умножения

Тип урока

Изучение
и первичное закрепление новых знаний и способов действий

Цели

Обучающие:
организовать деятельность обучающихся по изучению нового материала.

Развивающие: уметь
определять и формулировать цель урока с помощью учителя, планировать свои
действия в соответствии с поставленной задачей, высказывать свое
предположение.

Воспитательные:
создать условия для воспитания доброжелательного отношения друг к другу,
умения работать в коллективе, сотрудничать друг с другом; продолжить приучать
к аккуратности, внимательности.

Планируемые образовательные результаты

Предметные

Метапредметные

Личностные

Научится
выполнять умножение натуральных чисел, знать и уметь применять полученные
знания на практике.

Определять
и формулировать цель урока, работать по коллективно составленному плану,
уметь оформлять свои мысли в устной форме, слушать и понимать других,
выражать свои мысли точно и полно, уметь добывать знания, используя учебник.

Уметь
осуществлять самооценку на основе критерия успешности учебной деятельности.

Этапы проведения

Деятельность

Планируемые результат

учителя

учащихся

предметные

УУД

I.Мотивация
к учебной деятельности.

Цели:

— актуализировать
требования к учащемуся с позиций учебной деятельности,

—
создать условия для вовлечения учеников в учебную деятельность.

Создать
условия для вовлечения учеников в учебную деятельность

-Представим, что я живу в
трёхкомнатной квартире. В каждой комнате у меня лежит по два яблока. Сколько
всего яблок? (2+2+2)

— как можно по-другому записать
эту сумму? (2 × 3 =6)

— Как называется это
математическое действие? (умножением)

Из истории:

За всю историю
человечества было придумано много способов умножения. Только в конце XV —
начале XVI века
итальянский математик Лука Пачоли приводит 8 различных способов умножения об
арифметике.

Знак умножения
«косой крест»

(×) впервые
в 1631 году ввёл английский математик Уильям Оутред (1575 – 1660);

Позднее, в 1698
году, выдающийся немецкий математик Готфрид Лейбниц (1646 – 1716), ввёл знак
умножения «точка».

— Как называются все компоненты
этого действия? (2-множитель,3-множитель,6-произведение)

— А, если мы числа заменим на
буквы, то как будет выглядеть наше числовое выражение?

(а×b)

Отвечают
на вопросы.

Знать
компоненты произведения: первый множитель, второй множитель= произведение

Коммуникативные: уметь
совместно договариваться о правилах поведения и общения, оформлять свои мысли
в устной форме.

II.
Актуализация и выявление места и причины затруднения.

Цели:

-создать
условия для выполнения пробного учебного действия,

-выявить
в чём затрудняются учащиеся,

—
зафиксировать причину затруднения в речи.

Фиксирует
индивидуальные затруднения, выявляет места и причины затруднения в речи,
обобщает знания.

Как вы
уже поняли, тема нашего урока.

-Найдите
значения выражений

12×3 и 3×12

— Что вы
можете сказать?

(значения
двух выражений равны)

—
Давайте запишем в виде равенства (12×3=3×12)

-Как
записать его с помощью буквенной записи?

— Как
называется свойство, выражающее такой записью?

-Как вы
думаете, какие ещё свойства сложения будут выполняться для умножения?

(1× а и а×0)

Слушают
учителя, отвечают на вопросы

Учащиеся
формулируют тему урока

Знать
свойства умножения. Уметь их записывать с помощью буквенного равенства.

Познавательные:

Уметь
отличать новое от уже известного с помощью учителя, преобразовывать
информацию из одной формы в другую.

Коммуникативные:

Уметь
слушать и понимать речь других, оформлять свои мысли в устной и письменной
форме.

Регулятивные: уметь
проговаривать последовательность действий на уроке, высказывать свое
предположение.

Физкульминутка

Мы хорошо работаем, но пришла пора
физминутки. Она не простая, а математическая, проверим, насколько вы
внимательны. Я буду предлагать вам задания, если нужно ответить да – вы
поднимаете левую руку, если нет -правую.

1.
Числа,
которые используются при счете предметов, называют натуральными. (Да).

2.
Нуль
– это натуральное число. (Нет).

3.
В
натуральном ряду чисел есть первое число – 1. (Да).

4.
В
натуральном ряду чисел есть наибольшее число. (Нет).

5.
Знаки,
используемые для записи натуральных чисел, называются цифрами. (Да).

6.
Натуральные
числа, записанные с помощью одной цифры, называются однозначными. (Да)

7.
Натуральные
числа, записанные с помощью трех цифр, называются двухзначными. (Нет)

8.
Любое
натуральное число больше нуля. (Да).

9.
С
натуральными числами можно выполнять следующие действия: сложение, вычитание,
умножение, деление. (да).

Выполняют
упражнения

III.Первичное
закрепление с проговариванием.

Организовать
усвоение нового способа действий с проговариванием во внешней речи.

1)Работа
с учебником: с.110, № 384, №385(1,3)

2)Составь
выражение для решения задачи:

В двух
коробках лежат карандаши, причем

в одной
из них в 3 раза больше, чем в другой.

Сколько
карандашей в обеих коробках, если

в
меньшей их 12 штук?

(12×3+12=48)

3)
Решить удобным способом:

235 × 4 ×25
=

4 × 2121
× 5 =

50× 821 ×
4 =

Каким
свойством воспользуемся?

4) Задание:

Поменять
местами карточки, на которых записаны примеры с одинаковыми ответами.

Ты
примеры все реши, как зовут его, скажи!

Был он
долго неизвестным,

Но по
сказке интересной

Стал он
каждому знаком.

Он
весёлый, добрый, смелый,

Он
отважный и умелый.

В
царстве овощей живёт.

(Чиполино)

Выполняют
задание на доске и в тетрадях.

№384,
№385 комментирование решения.

Работают
со слайдом, устно.

Уметь
применять правила умножения.

Коммуникативные: уметь
выражать свои мысли с достаточной полнотой и точностью.

Регулятивные: уметь
проявлять свою волю в ситуации затруднения

Личностные: оценивать собственную учебную деятельность: свои
достижения, самостоятельность, инициативу, ответственность.

IV.Рефлексия
учебной деятельности на уроке.

Организовать
фиксирование нового содержания, рефлексию, самооценку учебной деятельности.

Ребята,
подведем итог работы на уроке.

— Какую
цель мы ставили на уроке? Мы ее достигли?

— Назовите
тему урока.

—
Расскажите, чему вы научились на уроке.

Домашнее
задание:

п.16, выучить
правила на с.106-107, №386,394

Регулятивные: уметь
оценивать правильность выполнения действия на уровне адекватной
ретроспективной оценки.

Личностные: уметь
осуществлять самооценку на основе критерия успешности учебной деятельности

Источник