Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.
Определение
Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.
НОК — это принятое для обозначения краткое название, собранной из первых букв.
Способы получения числа
Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.
Пример № 1
Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.
Пример № 2
Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:
Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.
Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.
Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:
1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.
2) НОК = 6300.
Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.
Проверка:
6300 / 300 = 21 — верно;
6300 / 1260 = 5 — верно.
Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.
Что значит НОК в математике
Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.
Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:
1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.
2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;
3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;
Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.
Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.
Проверка:
1) 3000 / 250 = 12 — верно;
2) 3000 / 600 = 5 — верно;
3) 3000 / 1500 = 2 — верно.
Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.
Еще один способ
В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение. Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:
1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.
2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.
3) Кратные 42: 84, 126, 168, 210, 252 и т. д.
Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД . Здесь мы поговорим про нахождение наименьшего общего кратного (НОК)
, и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b)
. Рассмотрим примеры нахождения НОК по приведенной формуле.
Пример.
Найдите наименьшее общее кратное двух чисел 126
и 70
.
Решение.
В этом примере a=126
, b=70
. Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b)
. То есть, сначала нам предстоит найти наибольший общий делитель чисел 70
и 126
, после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70)
, используя алгоритм Евклида: 126=70·1+56
, 70=56·1+14
, 56=14·4
, следовательно, НОД(126, 70)=14
.
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)=
126·70:14=630
.
Ответ:
НОК(126, 70)=630
.
Пример.
Чему равно НОК(68, 34)
?
Решение.
Так как 68
делится нацело на 34
, то НОД(68, 34)=34
. Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)=
68·34:34=68
.
Ответ:
НОК(68, 34)=68
.
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a
и b
: если число a
делится на b
, то наименьшее общее кратное этих чисел равно a
.
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители . Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел
.
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b)
. Действительно, произведение чисел a
и b
равно произведению всех множителей, участвующих в разложениях чисел a
и b
. В свою очередь НОД(a, b)
равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a
и b
(о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5
и 210=2·3·5·7
. Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7
. Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75
и в разложении числа 210
(такими множителями являются 3
и 5
), тогда произведение примет вид 2·3·5·5·7
. Значение этого произведения равно наименьшему общему кратному чисел 75
и 210
, то есть, НОК(75, 210)= 2·3·5·5·7=1 050
.
Пример.
Разложив числа 441
и 700
на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441
и 700
на простые множители:
Получаем 441=3·3·7·7
и 700=2·2·5·5·7
.
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7
. Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7
): 2·2·3·3·5·5·7·7
. Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100
.
Ответ:
НОК(441, 700)= 44 100
.
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a
добавить недостающие множители из разложения числа b
, то значение полученного произведения будет равно наименьшему общему кратному чисел a
и b
.
Для примера возьмем все те же числа 75
и 210
, их разложения на простые множители таковы: 75=3·5·5
и 210=2·3·5·7
. Ко множителям 3
, 5
и 5
из разложения числа 75
добавляем недостающие множители 2
и 7
из разложения числа 210
, получаем произведение 2·3·5·5·7
, значение которого равно НОК(75, 210)
.
Пример.
Найдите наименьшее общее кратное чисел 84
и 648
.
Решение.
Получаем сначала разложения чисел 84
и 648
на простые множители. Они имеют вид 84=2·2·3·7
и 648=2·2·2·3·3·3·3
. К множителям 2
, 2
, 3
и 7
из разложения числа 84
добавляем недостающие множители 2
, 3
, 3
и 3
из разложения числа 648
, получаем произведение 2·2·2·3·3·3·3·7
, которое равно 4 536
. Таким образом, искомое наименьшее общее кратное чисел 84
и 648
равно 4 536
.
Ответ:
НОК(84, 648)=4 536
.
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Теорема.
Пусть даны целые положительные числа a 1 , a 2 , …, a k
, наименьшее общее кратное m k
этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2)
, m 3 =НОК(m 2 , a 3)
, …, m k =НОК(m k−1 , a k)
.
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Пример.
Найдите НОК четырех чисел 140
, 9
, 54
и 250
.
Решение.
В этом примере a 1 =140
, a 2 =9
, a 3 =54
, a 4 =250
.
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9)
. Для этого по алгоритму Евклида определяем НОД(140, 9)
, имеем 140=9·15+5
, 9=5·1+4
, 5=4·1+1
, 4=1·4
, следовательно, НОД(140, 9)=1
, откуда НОК(140, 9)=140·9:НОД(140, 9)=
140·9:1=1 260
. То есть, m 2 =1 260
.
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54)
. Вычислим его через НОД(1 260, 54)
, который также определим по алгоритму Евклида: 1 260=54·23+18
, 54=18·3
. Тогда НОД(1 260, 54)=18
, откуда НОК(1 260, 54)=
1 260·54:НОД(1 260, 54)=
1 260·54:18=3 780
. То есть, m 3 =3 780
.
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250)
. Для этого находим НОД(3 780, 250)
по алгоритму Евклида: 3 780=250·15+30
, 250=30·8+10
, 30=10·3
. Следовательно, НОД(3 780, 250)=10
, откуда НОК(3 780, 250)=
3 780·250:НОД(3 780, 250)=
3 780·250:10=94 500
. То есть, m 4 =94 500
.
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500
.
Ответ:
НОК(140, 9, 54, 250)=94 500
.
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее
.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Пример.
Найдите наименьшее общее кратное пяти чисел 84
, 6
, 48
, 7
, 143
.
Решение.
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7
, 6=2·3
, 48=2·2·2·2·3
, 7
(7
– простое число , оно совпадает со своим разложением на простые множители) и 143=11·13
.
Для нахождения НОК данных чисел к множителям первого числа 84
(ими являются 2
, 2
, 3
и 7
) нужно добавить недостающие множители из разложения второго числа 6
. Разложение числа 6
не содержит недостающих множителей, так как и 2
и 3
уже присутствуют в разложении первого числа 84
. Дальше к множителям 2
, 2
, 3
и 7
добавляем недостающие множители 2
и 2
из разложения третьего числа 48
, получаем набор множителей 2
, 2
, 2
, 2
, 3
и 7
. К этому набору на следующем шаге не придется добавлять множителей, так как 7
уже содержится в нем. Наконец, к множителям 2
, 2
, 2
, 2
, 3
и 7
добавляем недостающие множители 11
и 13
из разложения числа 143
. Получаем произведение 2·2·2·2·3·7·11·13
, которое равно 48 048
.
Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».
Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.
Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.
Общее кратное натуральных чисел — число, которое делится на них без остатка.
Как найти наименьшее общее кратное чисел
Наименьшее общее кратное (НОК) чисел (двух, трех или больше) — это самое маленькое натурально число, которое делится на все эти числа нацело.
Чтобы найти НОК, можно использовать несколько способов.
Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.
Например, кратные числа 4 можно записать так:
К (4) = {8,12, 16, 20, 24, …}
К (6) = {12, 18, 24, …}
Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:
НОК (4, 6) = 24
Если числа большие, найти общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.
Для выполнения задания необходимо разложить предложенные числа на простые множители.
Сначала нужно выписать в строчку разложение наибольшего из чисел, а под ним — остальных.
В разложении каждого числа может присутствовать различное количество множителей.
Например, разложим на простые множители числа 50 и 20.
В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.
Теперь можно вычислить наименьшее общее кратное 20 и 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.
Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.
В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.
36 = 2 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3
16 = 2 * 2 * 2 * 2
Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).
Таким образом, их нужно добавить к разложению большего числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.
Например, НОК двенадцати и двадцати четырех будет двадцать четыре.
Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.
Например, НОК (10, 11) = 110.
Наибольший общий делитель
Определение 2
Если натуральное число a делится на натуральное число $b$, то $b$ называют делителем числа $a$, а число $a$ называют кратным числа $b$.
Пусть $a$ и $b$-натуральные числа. Число $c$ называют общим делителем и для $a$ и для $b$.
Множество общих делителей чисел $a$ и $b$ конечно, так как ни один из этих делителей не может быть больше, чем $a$. Значит,среди этих делителей есть наибольший, который называют наибольшим общим делителем чисел $a$ и $b$ и для его обозначения используют записи:
$НОД (a;b) или D (a;b)$
Чтобы найти наибольший общий делитель двух, чисел необходимо:
- Найти произведение чисел, найденных на шаге 2. Полученное число и будет искомым наибольшим общим делителем.
Пример 1
Найти НОД чисел $121$ и $132.$
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
Выбрать числа, которые входят в разложение этих чисел
$242=2cdot 11cdot 11$
$132=2cdot 2cdot 3cdot 11$
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=2cdot 11=22$
Пример 2
Найти НОД одночленов $63$ и $81$.
Будем находить согласно представленному алгоритму. Для этого:
Разложим числа на простые множители
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Выбираем числа, которые входят в разложение этих чисел
$63=3cdot 3cdot 7$
$81=3cdot 3cdot 3cdot 3$
Найдем произведение чисел, найденных на шаге 2.Полученное число и будет искомым наибольшим общим делителем.
$НОД=3cdot 3=9$
Найти НОД двух чисел можно и по-другому, используя множество делителей чисел.
Пример 3
Найти НОД чисел $48$ и $60$.
Решение:
Найдем множество делителей числа $48$: $left{{rm 1,2,3.4.6,8,12,16,24,48}right}$
Теперь найдем множество делителей числа $60$:$ left{{rm 1,2,3,4,5,6,10,12,15,20,30,60}right}$
Найдем пересечение этих множеств: $left{{rm 1,2,3,4,6,12}right}$- данное множество будет определять множество общих делителей чисел $48$ и $60$. Наибольший элемент в данном множестве будет число $12$. Значит наибольший общий делитель чисел $48$ и $60$ будет $12$.
Определение НОК
Определение 3
Общим кратным натуральных чисел
$a$ и $b$ называется натуральное число, которое кратно и $a$ и $b$.
Общими кратными чисел называются числа которые делятся на исходные без остатка.Например для чисел $25$ и $50$ общими кратными будут числа $50,100,150,200$ и т.д
Наименьшее из общих кратных будет называться наименьшим общим кратным и обозначается НОК$(a;b)$ или K$(a;b).$
Чтобы найти НОК двух чисел, необходимо:
- Разложить числа на простые множители
- Выписать множители, входящие в состав первого числа и добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Пример 4
Найти НОК чисел $99$ и $77$.
Будем находить согласно представленному алгоритму. Для этого
Разложить числа на простые множители
$99=3cdot 3cdot 11$
Выписать множители, входящие в состав первого
добавить к ним множители, которые входят в состав второго и не ходят в состав первого
Найти произведение чисел, найденных на шаге 2.Полученное число и будет искомым наименьшим общим кратным
$НОК=3cdot 3cdot 11cdot 7=693$
Составление списков делителей чисел часто очень трудоемкое занятие. Существует способ нахождение НОД, называемый алгоритмом Евклида.
Утверждения, на которых основан алгоритм Евклида:
Если $a$ и $b$ —натуральные числа, причем $avdots b$, то $D(a;b)=b$
Если $a$ и $b$ —натуральные числа, такие что $b
Пользуясь $D(a;b)= D(a-b;b)$, можно последовательно уменьшать рассматриваемые числа до тех пор, пока не дойдем до такой пары чисел, что одно из них делится на другое. Тогда меньшее из этих чисел и будет искомым наибольшим общим делителем для чисел $a$ и $b$.
Свойства НОД и НОК
- Любое общее кратное чисел $a$ и $b$ делится на K$(a;b)$
- Если $avdots b$ , то К$(a;b)=a$
Если К$(a;b)=k$ и $m$-натуральное число, то К$(am;bm)=km$
Если $d$-общий делитель для $a$ и $b$,то К($frac{a}{d};frac{b}{d}$)=$ frac{k}{d}$
Если $avdots c$ и $bvdots c$ ,то $frac{ab}{c}$ — общее кратное чисел $a$ и $b$
Для любых натуральных чисел $a$ и $b$ выполняется равенство
$D(a;b)cdot К(a;b)=ab$
Любой общийй делитель чисел $a$ и $b$ является делителем числа $D(a;b)$
Второе число:
b=
Разделитель разрядов
Без разделителя пробел » ´
Результат:
Наибольший общий делитель НОД(a
,b
)=6
Наименьшее общее кратное НОК(a
,b
)=468
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называется наибольшим общим делителем
(НОД) этих чисел. Обозначается НОД(a,b), (a,b), gcd(a,b) или hcf(a,b).
Наименьшее общее кратное
(НОК) двух целых чисел a и b есть наименьшее натуральное число, которое делится на a и b без остатка. Обозначается НОК(a,b), или lcm(a,b).
Целые числа a и b называются взаимно простыми
, если они не имеют никаких общих делителей кроме +1 и −1.
Наибольший общий делитель
Пусть даны два положительных числа a
1 и a
2 1). Требуется найти общий делитель этих чисел, т.е. найти такое число λ
, которое делит числа a
1 и a
2 одновременно. Опишем алгоритм.
1) В данной статье под словом число будем понимать целое число.
Пусть a
1 ≥ a
2 , и пусть
где m
1 , a
3 некоторые целые числа, a
3 a
2 (остаток от деления a
1 на a
2 должен быть меньше a
2).
Предположим, что λ
делит a
1 и a
2 , тогда λ
делит m
1 a
2 и λ
делит a
1 −m
1 a
2 =a
3 (Утверждение 2 статьи «Делимость чисел. Признак делимости»). Отсюда следует, что всякий общий делитель a
1 и a
2 является общим делителем a
2 и a
3 . Справедливо и обратное, если λ
общий делитель a
2 и a
3 , то m
1 a
2 и a
1 =m
1 a
2 +a
3 также делятся на λ
. Следовательно общий делитель a
2 и a
3 есть также общий делитель a
1 и a
2 . Так как a
3 a
2 ≤a
1 , то можно сказать, что решение задачи по нахождению общего делителя чисел a
1 и a
2 сведено к более простой задаче нахождения общего делителя чисел a
2 и a
3 .
Если a
3 ≠0, то можно разделить a
2 на a
3 . Тогда
,
где m
1 и a
4 некоторые целые числа, (a
4 остаток от деления a
2 на a
3 (a
4 a
3)). Аналогичными рассуждениями мы приходим к выводу, что общие делители чисел a
3 и a
4 совпадают с общими делителями чисел a
2 и a
3 , и также с общими делителями a
1 и a
2 . Так как a
1 , a
2 , a
3 , a
4 , … числа, постоянно убывающие, и так как существует конечное число целых чисел между a
2 и 0, то на каком то шаге n
, остаток от деления a
n на a
n+1 будет равен нулю (a
n+2 =0).

Каждый общий делитель λ
чисел a
1 и a
2 также делитель чисел a
2 и a
3 , a
3 и a
4 , …. a
n и a
n+1 . Справедливо и обратное, общие делители чисел a
n и a
n+1 являются также делителями чисел a
n−1 и a
n , …. , a
2 и a
3 , a
1 и a
2 . Но общий делитель чисел a
n и a
n+1 является число a
n+1 , т.к. a
n и a
n+1 без остатка делятся на a
n+1 (вспомним, что a
n+2 =0). Следовательно a
n+1 является и делителем чисел a
1 и a
2 .
Отметим, что число a
n+1 является наибольшим из делителей чисел a
n и a
n+1 , так как наибольший делитель a
n+1 является сам a
n+1 . Если a
n+1 можно представить в виде произведения целых чисел, то эти числа также являются общими делителями чисел a
1 и a
2 . Число a
n+1 называют наибольшим общим делителем
чисел a
1 и a
2 .
Числа a
1 и a
2 могут быть как положительными, так и отрицательными числами. Если один из чисел равен нулю, то наибольший общий делитель этих чисел будет равен абсолютной величине другого числа. Наибольший общий делитель нулевых чисел не определен.
Вышеизложенный алгоритм называется алгоритмом Евклида
для нахождения наибольшего общего делителя двух целых чисел.
Пример нахождения наибольшего общего делителя двух чисел
Найти наибольший общий делитель двух чисел 630 и 434.
- Шаг 1. Делим число 630 на 434. Остаток 196.
- Шаг 2. Делим число 434 на 196. Остаток 42.
- Шаг 3. Делим число 196 на 42. Остаток 28.
- Шаг 4. Делим число 42 на 28. Остаток 14.
- Шаг 5. Делим число 28 на 14. Остаток 0.
На шаге 5 остаток от деления равен 0. Следовательно наибольший общий делитель чисел 630 и 434 равен 14. Заметим, что числа 2 и 7 также являются делителями чисел 630 и 434.
Взаимно простые числа
Определение
1.
Пусть наибольший общий делитель чисел a
1 и a
2 равен единице. Тогда эти числа называются взаимно простыми числами
, не имеющими общего делителя.
Теорема
1.
Если a
1 и a
2 взаимно простые числа, а λ
какое то число, то любой общий делитель чисел λa
1 и a
2 является также общим делителем чисел λ
и a
2 .
Доказательство. Рассмотрим алгоритм Евклида для нахождения наибольшего общего делителя чисел a
1 и a
2 (см. выше).

Из условия теоремы следует, что наибольшим общим делителем чисел a
1 и a
2 , и следовательно a
n и a
n+1 является 1. Т.е. a
n+1 =1.
Умножим все эти равенства на λ
, тогда

Пусть общий делитель a
1 λ
и a
2 есть δ
. Тогда δ
входит множителем в a
1 λ
, m
1 a
2 λ
и в a
1 λ
—m
1 a
2 λ
=a
3 λ
(см. «Делимость чисел»,Утверждение 2). Далее δ
входит множителем в a
2 λ
и m
2 a
3 λ
, и, следовательно, входит множителем в a
2 λ
—m
2 a
3 λ
=a
4 λ
.
Рассуждая так мы убеждаемся, что δ
входит множителем в a
n−1 λ
и m
n−1 a
n λ
, и, следовательно, в a
n−1 λ
−m
n−1 a
n λ
=a
n+1 λ
. Так как a
n+1 =1, то δ
входит множителем в λ
. Следовательно число δ
является общим делителем чисел λ
и a
2 .
Рассмотрим частные случаи теоремы 1.
Следствие
1.
Пусть a
и c
простые числа относительно b
. Тогда их произведение ac
является простым числом относительно b
.
Действительно. Из теоремы 1 ac
и b
имеют тех же общих делителей, что и c
и b
. Но числа c
и b
взаимно простые, т.е. имеют единственный общий делитель 1. Тогда ac
и b
также имеют единственный общий делитель 1. Следовательно ac
и b
взаимно простые.
Следствие
2.
Пусть a
и b
взаимно простые числа и пусть b
делит ak
. Тогда b
делит и k
.
Действительно. Из условия утверждения ak
и b
имеют общий делитель b
. В силу теоремы 1, b
должен быть общим делителем b
и k
. Следовательно b
делит k
.
Следствие 1 можно обобщить.
Следствие
3.
1. Пусть числа a
1 , a
2 , a
3 , …, a
m простые относительно числа b
. Тогда a
1 a
2 , a
1 a
2 ·a
3 , …, a
1 a
2 a
3 ···a
m , произведение этих чисел простое относительно числа b
.
2. Пусть имеем два ряда чисел
таких, что каждое число первого ряда простое по отношению каждого числа второго ряда. Тогда произведение
Требуется найти такие числа, которые делятся на каждое из этих чисел.
Если число делится на a
1 , то оно имеет вид sa
1 , где s
какое-нибудь число. Если q
есть наибольший общий делитель чисел a
1 и a
2 , то
где s
1 — некоторое целое число. Тогда
является наименьшим общим кратным чисел
a
1 и a
2 .
a
1 и a
2 взаимно простые, то наименьшее общее кратное чисел a
1 и a
2:
Нужно найти наименьшее общее кратное этих чисел.
Из вышеизложенного следует, что любое кратное чисел a
1 , a
2 , a
3 должно быть кратным чисел ε
и a
3 , и обратно. Пусть наименьшее общее кратное чисел ε
и a
3 есть ε
1 . Далее, кратное чисел a
1 , a
2 , a
3 , a
4 должно быть кратным чисел ε
1 и a
4 . Пусть наименьшее общее кратное чисел ε
1 и a
4 есть ε
2 . Таким образом выяснили, что все кратные чисел a
1 , a
2 , a
3 ,…,a
m совпадают с кратными некоторого определенного числа ε
n , которое называют наименьшим общим кратным данных чисел.
В частном случае, когда числа a
1 , a
2 , a
3 ,…,a
m взаимно простые, то наименьшее общее кратное чисел a
1 , a
2 как было показано выше имеет вид (3). Далее, так как a
3 простое по отношению к числам a
1 , a
2 , тогда a
3 простое по отношению числа a
1 ·a
2 (Следствие 1). Значит наименьшее общее кратное чисел a
1 ,a
2 ,a
3 является число a
1 · a
2 ·a
3 . Рассуждая аналогичным образом мы приходим к следующим утверждениям.
Утверждение
1.
Наименьшее общее кратное взаимно простых чисел a
1 , a
2 , a
3 ,…,a
m равен их произведению a
1 ·a
2 ·a
3 ···a
m .
Утверждение
2.
Любое число, которое делится на каждое из взаимно простых чисел a
1 , a
2 , a
3 ,…,a
m делится также на их произведение a
1 ·a
2 ·a
3 ···a
m .

Делимость натуральных чисел
6 класс
Урок обобщения и систематизации знаний.
Озым Эрзи Акимовна
Учитель математики МБОУ «СОШ № 2 им. Х.Я.Беретаря» г. Адыгейска

Цели урока
— обобщить и систематизировать знания учащихся по данной теме;
повторить понятия делителя и кратных чисел, повторить признаки делимости суммы и разности чисел;
признаки делимости на 2, 3,4, 5, 9, 10, 25;
повторить признаки делимости и закрепить их знание при разложении чисел на простые множители;
повторить алгоритм нахождения НОК и НОД чисел;
— закрепить навыки и умения применения знаний по теме к решению упражнений.

Сведения из истории
Лиши все вещи на свете их числа, и они перестанут существовать.
Исидор Севильский

Натуральные числа
Первые представления о числе приобретены людьми в незапамятной древности. Они возникли из счета людей, животных, плодов, различных изделий человека и других предметов. Результатом счета являются один, два, три и т.д. Эти числа называются теперь натуральными. В арифметике их называют также целыми. Ряд целых чисел 1, 2, 3, 4, 5… продолжается без конца; он называется натуральным рядом.

Евклид (III в. до н.э.) определял число (натуральное) как «множество, составленное из единиц».

На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух или трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много».

С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах. Для этого человек пользовался окружающими его предметами как инструментами счета: он делал зарубки на палках и деревьях, завязывал узлы на веревках, складывал камешки и кучки и т.п.
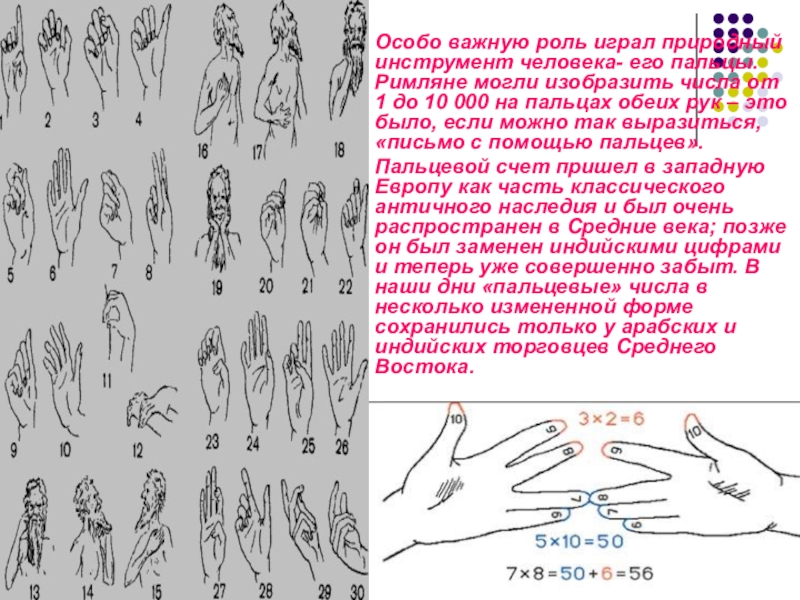
Особо важную роль играл природный инструмент человека- его пальцы. Римляне могли изобразить числа от 1 до 10 000 на пальцах обеих рук – это было, если можно так выразиться, «письмо с помощью пальцев».
Пальцевой счет пришел в западную Европу как часть классического античного наследия и был очень распространен в Средние века; позже он был заменен индийскими цифрами и теперь уже совершенно забыт. В наши дни «пальцевые» числа в несколько измененной форме сохранились только у арабских и индийских торговцев Среднего Востока.

Древние египтяне, индусы, греки и римляне производили расчеты на счетных досках.
Японский соробан
Азиатская ручная абака

Делители и кратные
Если одно натуральное число нацело делится на другое натуральное число, то первое называют кратным второму, а второе – делителем первого.
Таким образом, если а и в – натуральные числа и а делится на в нацело, то а кратно в, а в – делитель а. например, из того, что 45 : 9 = 5, следует, что 45 кратно 9, а 9 – делитель числа 45.
Любое натуральное число имеет бесконечно много кратных.
Пример. 1)Укажите все делители числа 45. 2) Укажите числа, которым кратно число 45.
Решение. 1) Делителями числа 45 будут числа 1; 3; 5; 9; 15; 45.
2) Кратными числу 45 будут числа 45; 90; 135; 180…

Делимость произведения
Если хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.
Пример. Найдите частное: (15ху) : 5; (18аb) : 18.
Решение. (15ху) : 5 = (15:5)ху = 3ху.
(18аb) : 18 = (18:18)аb = аb

Делимость суммы и разности чисел
Свойство 1. Если а : b и с : b, то ( а+с) : b. Например, из того, что 12:3 и 21 :3, можно сдать вывод, что (12+21) : 3.
Свойство 2. Если а : b и с не делится на b, то а + с не делится на b.
Например, из того, что 12:3 и 22 не делится на 3, можно сделать вывод, что 12+22 не делится на 3.
Свойство 3. Если а : b и (а+с) : b, то с: b.
Например, из того, что 12:3 и (12+21) : 3, можно сделать вывод, что 21 :3.
Свойство 4. Если а : с и с : b, то а : b.
Например, из того, что 48 : 6 и 6 : 3, можно сделать вывод, что 48:3.
Если и уменьшаемое, и вычитаемое делятся на некоторое число, то и разность делится на это число.

Признаки делимости на 2,3,4,5,9,10 и 25.
Если последняя цифра числа четная, то оно делится на 2.
Если последняя цифра числа 5 или 0, то оно делится на 5.
Если число оканчивается цифрой 0, то оно делится на 10.
Число делится на 4, если две последние его цифры нули или образуют число, делящееся на 4.
Натуральное число делится на 3 тогда и только тогда, когда делится на 3 сумма его цифр.
Натуральное число делится на 9 тогда и только тогда, когда делится на 9 сумма его цифр.
Число делится на 6, если оно делится одновременно на 2 и на 3.
На 11 делятся только те числа, у которых сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо разнится от нее на число, делящееся на 11.
На 25 делятся числа, две последние цифры которых нули или образуют число, делящееся на 25.( То есть числа, оканчивающиеся на 00, 25, 50 или 75).

Простые и составные числа
Натуральные числа, имеющие только два делителя, называют простыми.
Натуральные числа, имеющие более двух делителей, называют составными.
Число 1 не относится ни к простым, ни к составным числам.
Например: 2, 3, 5, 7- простые числа. 4,6,8,9, 10 – составные числа.
Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители.
Например, 3528=23 * 32 * 72
Основная теорема арифметики: любое натуральное число ( кроме 1) либо является простым , либо его можно разложить на простые множители, причем единственным способом.

Разложение числа на простые множители
При разложении числа на простые множители используют признаки делимости и применяют запись столбиком, при которой делитель располагают справа от вертикальной черты, а частное записывают под делимым.
Например: разложите на простые множители число: 1) 6468, 2) 3780.
Решение : 6468 2 3780 2
3234 2 1890 2
1617 3 945 3
539 7 315 3
77 7 105 3
11 11 35 5
1 7 7
6468= 22 *31 * 72 * 111 1
3780= 22 * 33 * 51 * 71

Нахождение наибольшего общего делителя и наименьшего общего кратного.
Числа, которые одновременно являются делителями некоторых чисел, называют их общими делителями.
Наибольший общий делитель чисел m и n обозначают НОД (m;n).
Например, НОД(28; 42) = 14.
Найдите НОД чисел 12 и 18.
12=22 * 31 , 18= 21 * 32 100 = 22 * 52 , 40 = 23 * 51
6= 21 * 31 20 = 22* 51

Взаимно простые числа. Признак делимости на произведение.
Числа, наибольший общий делитель которых равен 1, называют взаимно простыми.
Например, взаимно простыми являются числа 18 и 35, хотя каждое из них – составное число. В самом деле, у числа 18 шесть делителей: 1,2,3,4,6,9 и 18, а у числа 35 четыре делителя: 1,5,7 и 35. общих делителей, отличных от 1, у чисел 18 и 35 нет.
Признак делимости на произведение взаимно простых чисел: если число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.

Алгоритм нахождения наименьшего общего кратного
1) Разложить данные числа на простые множители.
2) Выписать все простые числа, которые входят хотя бы в одно из полученных разложений.
3) Каждое из выписанных простых чисел взять с наибольшим из показателей степени, с которым оно входит в разложения данных чисел.
4) Записать произведение полученных степеней.
Пример. Найдите НОК 12 и 18.
Решение. 12= 22 * 31 , 18 = 21 * 32
36 = 22 * 32
Для любых натуральных чисел а и b справедливо равенство
НОД(а;b) * НОК (а;b) = ab

Тест №1
1. Укажите выражения, значения которых:
а) кратны 2: 12+16; 25+14; 22-11; 3+21;
б) кратны 3: 17+33; 60*7+5; 10*6+3; 18*2+9
2. Даны числа : 249; 44; 3050; 7855; 9296; 7050. Укажите, какие из них:
а) кратны 2;
б) делятся на 5, но не делятся на 2;
в) кратны 10.
3.Даны числа: 192, 824, 521, 714, 976. Выпишите из них те, которые делятся на 4.
4. Даны числа: 760, 675, 455, 320, 850. Выпишите из них те, которые кратны 25.
5. Из магазина мама принесла несколько пакетов с мандаринами, по 5 мандаринов в каждом пакете. Могла ли она принести 27 мандаринов? 45 мандаринов? 32 мандарина? Ответ обосновать.

Тест № 2
Напишите все четные числа, которые удовлетворяют неравенству 18
Выпишите числа, которые делятся на 3; на 9: 123; 834; 675; 225; 1004; 882; 1111; 2341; 7235; 2385; 6264. Верно ли утверждение: а) если число делится на 9, то оно делится на 3; б) если число делится на 3,то оно делится на 9? Ответ обоснуйте. Приведите примеры.
Найдите частное: 1)(18ав) : (6а); 2) (45ху) : (5х).
Даны числа : 11, 54, 47, 132, 1, 23, 65, 3 и 78. Укажите, какие из них являются: а) простыми; б) составными.
Разложите на простые множители: а) 20; б) 72; в) 150.
Найдите НОК и НОД чисел 126 и 84, 105 и 924.




