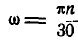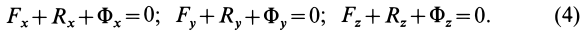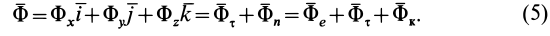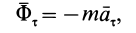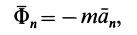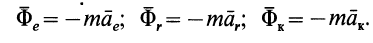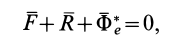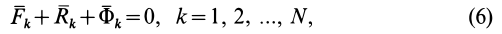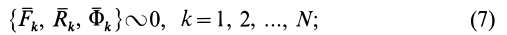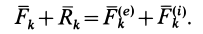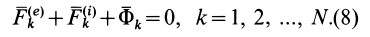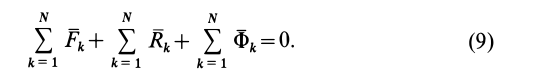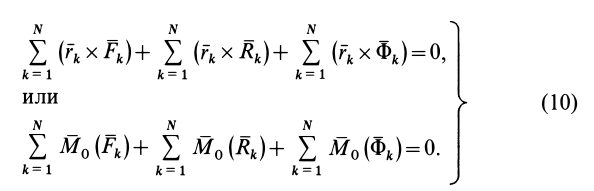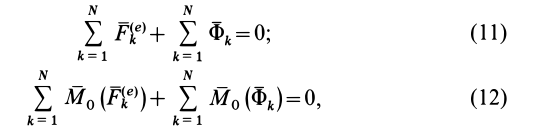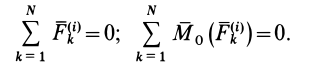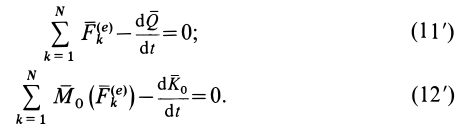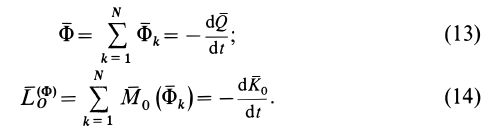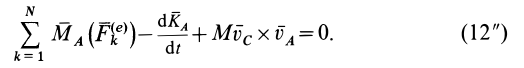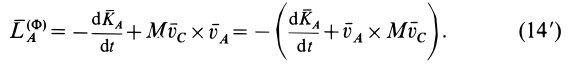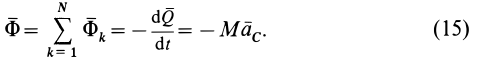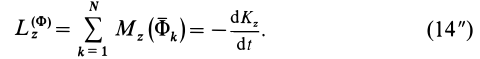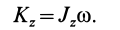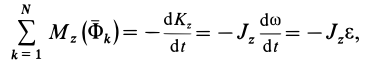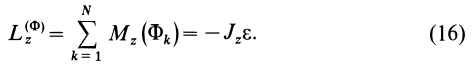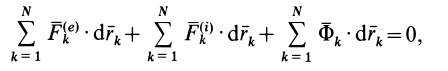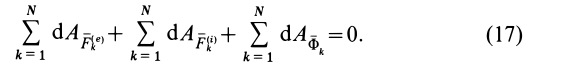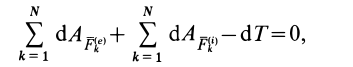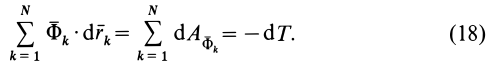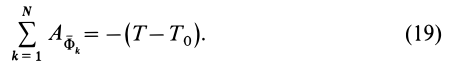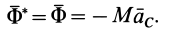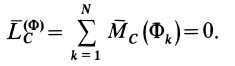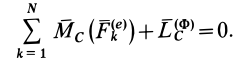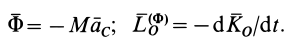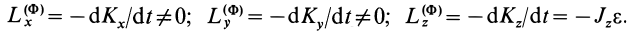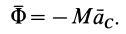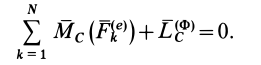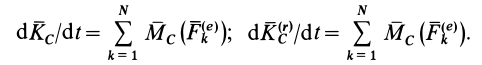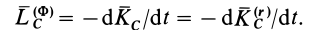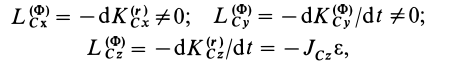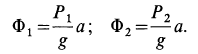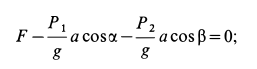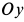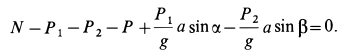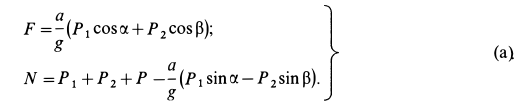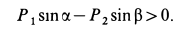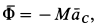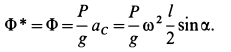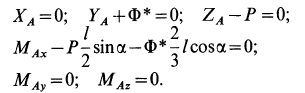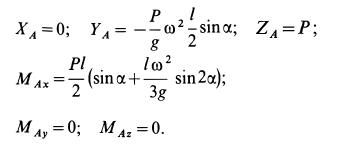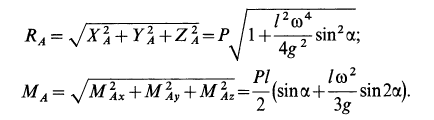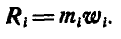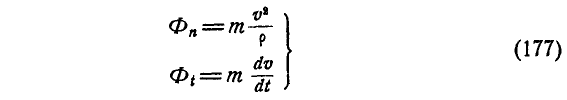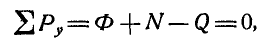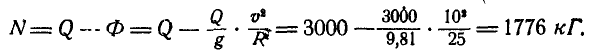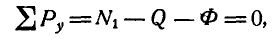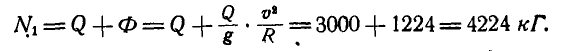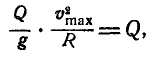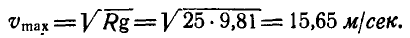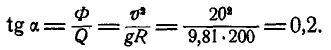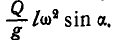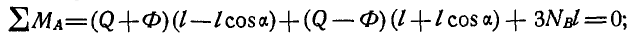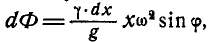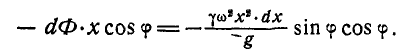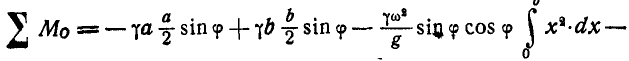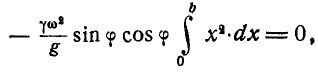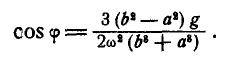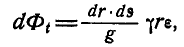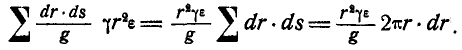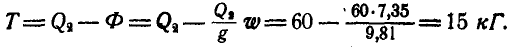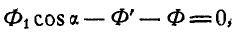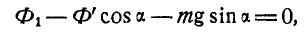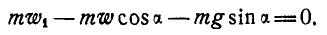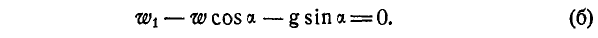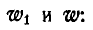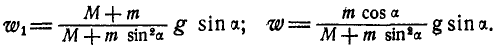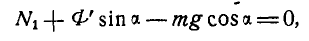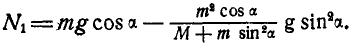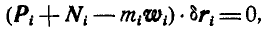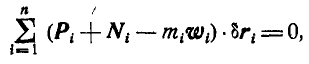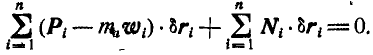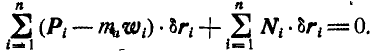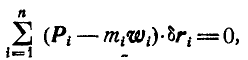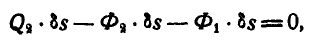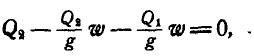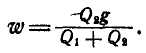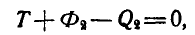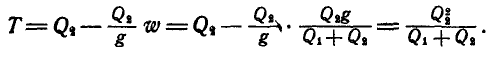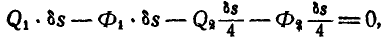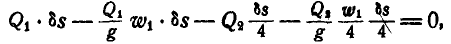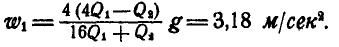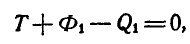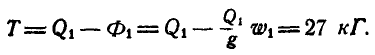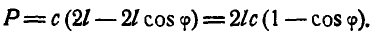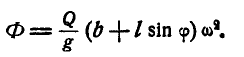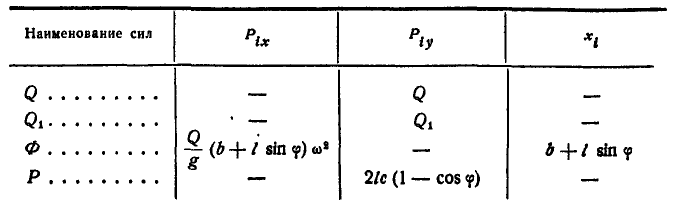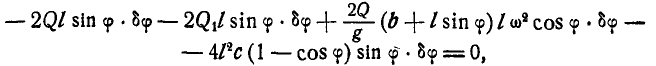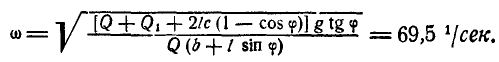Разлагать на составляющие как пишется

Физика и математика не обходятся без понятия «векторная величина». Это необходимо знать и распознавать, а также уметь управлять им. Обязательно стоит научиться, чтобы не запутаться и избежать глупых ошибок.

Как отличить скалярную величину от векторной?

У первого всегда есть только одна характеристика. Это его числовое значение. Большинство скаляров могут быть как положительными, так и отрицательными. Примеры включают электрический заряд, работу или температуру. Но есть скаляры, которые не могут быть отрицательными, например длина и масса.

Векторная величина, помимо числовой, всегда взятой по модулю, также характеризуется направлением. Поэтому его можно представить графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенном направлении.

При письме каждая векторная величина обозначается стрелкой на букве. Если мы говорим о числовом значении, то стрелка не пишется или берется по модулю.

Какие действия чаще всего выполняются с векторами?

Сначала противостояние. Они могут быть, а могут и не совпадать. В первом случае их модули совпадают. Но это не единственное условие. Они также должны иметь равные или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположностями. Если хотя бы одно из указанных условий не выполняется, векторы не равны.

Затем идет добавление. Это можно сделать по двум правилам: треугольник или параллелограмм. Первый предписывает сначала отложить вектор, затем второй — от его конца. Результатом сложения будет то, что нужно нарисовать от начала первого до конца второго.

Правило параллелограмма можно использовать, когда вам нужно добавить векторные величины в физике. В отличие от первого правила, здесь их следует отложить на один балл. Затем соберите их до параллелограмма. Результатом действия нужно считать диагональ параллелограмма, проведенную из той же точки.

Если одну векторную величину вычесть из другой, они снова откладываются от точки. Только результатом будет вектор, равный вектору, проведенному от конца второго до конца первого.

Какие векторы изучают в физике?

Их столько, сколько скаляров. Вы можете только вспомнить, какие векторные величины существуют в физике. Или узнать признаки, по которым их можно вычислить. Тем, кто отдает предпочтение первому варианту, такой столик пригодится. Перечисляет основные векторные физические величины.

Обозначение формулы	Имя
v	скорость
р	в движении
а	ускорение
Ф	сила
р	пульсировать
А ТАКЖЕ	напряженность электрического поля
В	магнитная индукция
М	момент силы

Теперь немного подробнее о некоторых из этих ценностей.

Первая величина — скорость

Начать стоит, чтобы привести примеры векторных величин. Это связано с тем, что он изучается одним из первых.

Скорость определяется как характеристика движения тела в пространстве. Задайте числовое значение и направление. Итак, скорость — это векторная величина. Кроме того, его принято делить на виды. Первый — это линейная скорость. Он вводится при рассмотрении равномерного прямолинейного движения. В этом случае он оказывается равным отношению пути, пройденного телом, и времени движения.

Эту же формулу можно использовать для нерегулярных движений. Только тогда он будет средним. Кроме того, выбираемый временной интервал должен быть как можно короче. Когда временной интервал стремится к нулю, значение скорости уже мгновенное.

Если рассматривать произвольное движение, то здесь скорость всегда является векторной величиной. Ведь его нужно разложить на прямые составляющие по каждому вектору, который направляет координатные линии. Кроме того, он определяется как производная по времени от радиус-вектора.

Вторая величина — сила

Он определяет меру силы воздействия, которое приходит на тело от других тел или полей. Поскольку сила является векторной величиной, она обязательно имеет значение по величине и направлению. Поскольку он действует на тело, то здесь также важна сила. Чтобы получить визуальное представление о векторах силы, вы можете обратиться к следующей таблице.

Власть	Пункт применения	Направление
строгость	центр тела	в центре земли
вселенская гравитация	центр тела	в центре другого тела
эластичность	место контакта взаимодействующих тел	от внешних воздействий
трение	между соприкасающимися поверхностями	в обратном направлении движения

Кроме того, результирующая сила также является векторной величиной. Он определяется как сумма всех механических сил, действующих на тело. Для его определения необходимо провести сложение по принципу правила треугольника. Вам просто нужно отложить векторы по очереди с конца предыдущего. Результатом будет то, что связывает начало первого с концом последнего.

Третья величина — перемещение

Во время движения тело описывает определенную линию. Это называется траектория. Эта строчка может быть совершенно разной. Важнее не внешний вид, а начальная и конечная точки движения. Они соединены линией, называемой сдвигом. Это тоже векторная величина. Кроме того, он всегда направлен от начала движения к точке, где движение было остановлено. Его принято обозначать латинской буквой r.

Здесь может возникнуть вопрос: «Является ли путь векторной величиной?» В общем, это утверждение не соответствует действительности. Путь равен длине пути и не имеет определенного направления. Исключением является ситуация, когда рассматривается прямолинейное движение в одном направлении. Следовательно, величина вектора смещения совпадает по величине с траекторией, и их направление оказывается таким же. Следовательно, при рассмотрении движения по прямой без изменения направления движения, путь может быть включен в примеры векторных величин.

Четвертая величина — ускорение

это характеристика скорости изменения скорости. Кроме того, ускорение может иметь как положительные, так и отрицательные значения. При движении по прямой он направлен в сторону большей скорости. Если движение происходит по криволинейной траектории, вектор его ускорения раскладывается на две составляющие, одна из которых направлена ​​к центру кривизны по радиусу.

Среднее и мгновенное значения ускорения разделены. Первое следует рассчитывать как отношение изменения скорости за определенный период времени к этому времени. Когда рассматриваемый временной интервал стремится к нулю, мы говорим о мгновенном ускорении.

Пятая величина — импульс

По-другому его еще называют количеством движения. Импульс — это векторная величина, потому что она напрямую связана со скоростью и силой, прилагаемой к телу. У них обоих есть направление и импульс.

По определению, последняя равна произведению веса тела и скорости. Используя понятие количества движения тела, вы можете иначе написать известный закон Ньютона. Оказывается, изменение количества движения равно произведению силы на временной интервал.

В физике важную роль играет закон сохранения количества движения, который гласит, что в замкнутой системе тел его полный импульс постоянен.

Мы очень кратко перечислили, какие (векторные) величины изучаются в курсе физики.

Задача о неупругом ударе

Состояние. На путях есть стационарная площадка. К вам приближается карета со скоростью 4 м / с. Вес платформы и вагона — 10 и 40 тонн соответственно. Автомобиль ударяется о платформу, происходит автоматическое сцепление. Необходимо рассчитать скорость системы платформы автомобиля после удара.

Решение. Сначала необходимо ввести следующие обозначения: скорость автомобиля до удара — v1, машина с платформой после спаривания — v, масса машины — m1, платформа — m2. В зависимости от состояния задачи необходимо знать значение скорости v.

Правила решения таких задач требуют схематического изображения системы до и после взаимодействия. Ось OX целесообразно направить по рельсам в направлении движения каретки.

В этих условиях транспортную систему можно считать закрытой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, трение о рельсы не учитывается.

Согласно закону сохранения количества движения их векторная сумма до взаимодействия между автомобилем и платформой равна общей для сцепления после удара. Сначала платформа не двигалась, поэтому ее импульс был нулевым. Переместилась только машина, ее импульс — произведение m1 и v1.

Поскольку удар был неупругим, то есть автомобиль зацепился за платформу, а затем начал катиться вместе в одном направлении, импульс системы не изменил направление. Но его значение изменилось. А именно произведением суммы массы автомобиля с платформой на требуемую скорость.

Вы можете записать это равенство: m1 * v1 = (m1 + m2) * v. Это будет верно для проекции векторов момента на выбранную ось. Легко вывести равенство, которое потребуется для вычисления желаемой скорости: v = m1 * v1 / (m1 + m2).

Согласно правилам, значения массы следует переводить из тонн в килограммы. Поэтому, когда вы подставляете их в формулу, вы должны сначала умножить известные значения на тысячу. Простые вычисления дают число 0,75 м / с.

Отвечать. Скорость вагона-платформы 0,75 м / с.

Задача с разделением тела на части

Состояние. Скорость летящей гранаты — 20 м / с. Он разделен на две части. Масса первого 1,8 кг. Продолжайте движение в том направлении, в котором летела граната, со скоростью 50 м / с. Второй осколок имеет массу 1,2 кг. Насколько это быстро?

Решение. Обозначьте массы фрагментов буквами m1 и m2. Их скорости будут v1 и v2 соответственно. Начальная скорость гранаты v. В задаче надо вычислить значение v2.

Чтобы более крупный осколок продолжал двигаться в том же направлении, что и вся граната, второй должен лететь в противоположном направлении. Если выбрать направление оси, которое было при начальном импульсе, то после разрыва большой фрагмент летит вдоль оси, а маленький — против оси.

В этой задаче допустимо использование закона сохранения количества движения в связи с тем, что взрыв гранаты происходит мгновенно. Поэтому, несмотря на то, что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его величиной по абсолютной величине.

Сумма значений вектора импульса после взрыва гранаты такая же, как и раньше. Если написать закон сохранения количества движения тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Легко выразить требуемую скорость. Он будет определяться по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м / с.

Отвечать. Скорость маленького осколка — 25 м / с.

Задача про выстрел под углом

Состояние. Пушка установлена ​​на платформе массой M. Из нее выстреливается снаряд массой m. Он взлетает под углом α к горизонту со скоростью v (заданной относительно земли). Необходимо знать значение скорости платформы после выстрела.

Решение. В этой задаче можно использовать закон сохранения количества движения в проекции на ось OX. Но только в том случае, если проекция возникающих внешних сил равна нулю.

Для направления оси OX нужно выбрать сторону, по которой будет лететь пуля, и параллельную горизонтальной линии. В этом случае проекции сил тяжести и реакция опоры на OX будут равны нулю.

Проблема будет решена в общем виде, так как конкретных данных для известных значений нет. Ответ — формула.

Импульс системы перед выстрелом был равен нулю, так как платформа и пуля были неподвижны. Пусть требуемая скорость платформы обозначается латинской буквой u. Тогда его импульс после выстрела будет определяться как произведение массы и проекции скорости. Поскольку платформа будет втягиваться (против направления оси OX), значение импульса будет со знаком минус.

Импульс снаряда является произведением его массы и проекции скорости на ось OX. Из-за того, что скорость направлена ​​под углом к ​​горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквальном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из него путем несложных преобразований получается формула ответа: u = (mv * cos α) / M.

Отвечать. Скорость платформы определяется по формуле u = (mv * cos α) / M.

Задача о переправе через реку

Состояние. Ширина реки по всей длине одинакова и равна, берега параллельны. Известны скорость потока воды в реке v1 и собственная скорость лодки v2. 1). При переправе нос лодки направлен строго на противоположный берег. Как далеко он уйдет вниз по течению? 2). Под каким углом α нужно ориентировать нос лодки так, чтобы она доходила до противоположного берега строго перпендикулярно начальной точке? Сколько времени займет такой переход?

Решение. 1). Максимальная скорость лодки — это векторная сумма двух значений. Первый из них — течение реки, которая направляется по берегам. Второй — собственная скорость лодки перпендикулярно берегу. На чертеже изображены два одинаковых треугольника. Первый формируется шириной реки и расстоянием, пройденным лодкой. Второй — из векторов скорости.

Следующая запись следует: s / l = v1 / v2. После преобразования получается формула искомого значения: s = l * (v1 / v2).

2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться собственный вектор скорости, равен отношению между модулями v1 и v2. Чтобы рассчитать время в пути, вам нужно разделить ширину реки на рассчитанную максимальную скорость. Величина последнего рассчитывается по теореме Пифагора.

v = (v22 — v12), поэтому t = l / (√ (v22 — v12)).

Отвечать. 1) s = l * (v1 / v2), 2) sin α = v1 / v2, t = l / (√ (v22 — v12)).

Содержание:

Принцип Даламбера для материальной точки:

Законы Ньютона содержат в себе все необходимое для рассмотрения движения любых механических систем. Но первоначально они применялись только для рассмотрения движения свободной материальной точки и свободного твердого тела до тех пор, пока не была дополнительно сформулирована аксиома связей. Для рассмотрения движения несвободных систем Даламбер предложил специальный принцип, получивший название принципа Даламбера. Этот принцип был сформулирован в терминах «потерянных» движений.

В настоящее время, когда считается справедливой аксиома связей, уравнения движения несвободной материальной точки являются такими же, как и для свободной, только к действующим на точку активным или заданным силам добавляют силы реакций связей.

Современное выражение принципа Даламбера не отличается по содержанию от уравнений движения материальной точки, но для многих задач оно более удобно. Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики. Для несвободной точки он эквивалентен основному закону вместе с аксиомой связей.

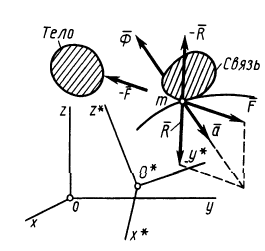
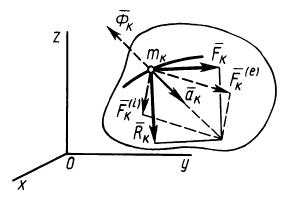
Уравнение движения материальной точки массой m относительно инерциальной системы отсчета под действием приложенных активных сил и реакций связей имеет вид

Рис. 82

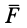
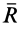
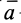
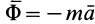
Сила является _ равнодействующей активных сил, — равнодействующей реакций связей,  — ускорением точки относительно инерциальной системы отсчета. Назовем силой инерции материальной точки произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. . Если использовать понятие силы инерции точки и перенести все слагаемые (1) в правую часть уравнения, то получим

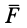
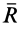
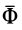
Так как силы , и (рис. 82) образуют систему сходящихся сил и удовлетворяют условию (2), то они являются системой сил, эквивалентной нулю, т. е.

Уравнение (2) или эквивалентное ему условие (3) выражает принцип Даламбера для точки: при движении материальной точки активные силы и реакции связей вместе с силой инерции точки образуют равновесную систему сил.

Из (2) в проекциях на координатные оси получаем три условия равновесия сил:

Ускорение точки относительно инерциальной системы отсчета. можно разложить на составляющие по осям декартовой системы координат, а также на касательное и нормальное ускорения и на переносное, относительное ускорения и ускорение Кориолиса, если движение точки считать сложным, состоящим из переносного и относительного. Соответственно силу инерции 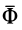можно разложить на такие же составляющие:

Касательная сила инерции

где 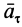— касательное ускорение; нормальная, или центробежная, сила инерции

где 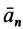— нормальное ускорение. Переносная и относительная силы инерции, а также сила инерции Кориолиса через ускорения выражаются соответственно так:

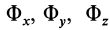
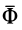
Аналогично выражаются через проекции ускорения на прямоугольные оси координат проекции силы инерции . На силы инерции существует несколько точек зрения. Согласно первой точке зрения, сила инерции условно прикладывается к точке, чтобы уравнению движения (1) придать более удобную форму условия равновесия (2). Поэтому силу инерции называют фиктивной, даламберовой, условной и т. д. С этой точки зрения силы инерции в принципе Даламбера не являются настоящими, реальными силами и отличаются не только от обычных сил, создаваемых действием тел, но даже и от сил инерции в относительном движении.

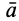
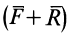
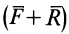
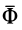
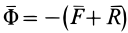
Согласно другой, наиболее распространенной точке зрения, сила инерции считается приложенной по частям к «ускоряющим» телам. Для обоснования приводят следующие рассуждения. Материальная точка движется с ускорением потому  что на нее действуют какие-то тела с силой, равной  (см. рис. 83). По закону о равенстве сил действия и противодействия материальная точка должна оказывать противодействие этим телам с такой же по модулю, но противоположной по направлению силой — , которая, согласно (2), равна силе инерции , т.е. .

Это соотношение дает основание считать, что сила инерции приложена к «ускоряющим» телам, т. е. телам, которые сообщают точке ускорение.

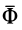
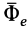
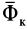
Действительно, сила инерции является векторной суммой сил действия точки на «ускоряющие» ее тела. Она служит суммарной оценкой этого действия. Однако при рассмотрении относительного движения_точки вводятся переносная и кориолисова силы инерции . Для подвижного наблюдателя их следует считать приложенными к движущейся материальной точке, но для них невозможно указать материальные тела, действием которых на точку можно объяснить эти силы.

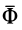
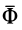
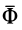
Переносная и кориолисова силы инерции являются частью полной силы инерции . Если для части силы невозможно указать тела, которые ее создают, то это же справедливо и для всей силы инерции . Однако в рассматриваемом случае указывается материальный объект, который действует с силой инерции на ускоряющие тела. Этим объектом является движущаяся с ускорением материальная точка.

Согласно третьей точке зрения, силу инерции считают приложенной к движущейся материальной точке, по крайней мере это справедливо для наблюдателя, который находится в собственной системе отсчета этой точки. Собственной системой отсчета материальной точки называют такую систему отсчета, относительно которой точка находится в покое, т. е. относительно которой ее относительные скорость и ускорение равны нулю. В этой системе отсчета справедливо условие относительного равновесия для сил

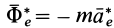
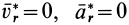
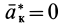
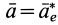
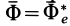
где — переносная сила инерции в собственной системе отсчета. Но в собственной системе отсчета и кориолисово ускорение , а тогда и, следовательно, .

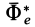
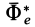
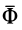
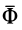
Таким образом, принцип Даламбера есть условие относительного равновесия для сил в собственной системе отсчета. Относительно собственного наблюдателя сила инерции приложена к движущейся точке, а следовательно, к ней приложена и совпадающая с  перенорной силой инерции в собственной системе отсчета сила инерции абсолютного движения . Силу в этом случае считают дополнительным действием на точку поля Вселенной. Такая точка зрения на силы инерции требует изменения понятия приложенной силы и изменения некоторых основных аксиом динамики (см. Приложение).

Принцип Даламбера для системы материальных точек

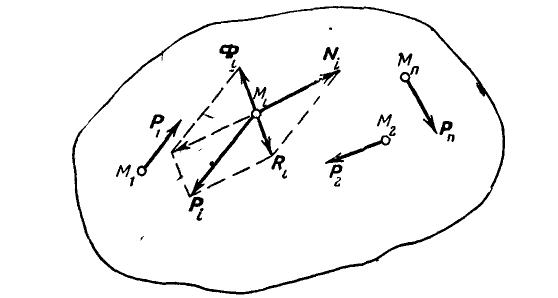
Рассмотрим систему 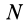материальных точек. К каждой точке системы в общем случае приложены равнодействующая активных сил и равнодействующая реакций связей. Применяя принцип Даламбера к каждой точке системы, получим

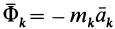
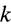
где  — сила инерции для -й точки (рис.83). Условия (6) можно представить в эквивалентной форме:

N векторных условий (6) или (7) выражают принцип Даламбера для системы: при движении механической системы активная сила и реакция связей вместе с силой инерции составляют равновесную систему сил для каждой точки системы.

Принцип Даламбера для системы по своему содержанию не отличается от уравнений движения точек системы.

Представим равнодействующую силу, приложенную к каждой точке системы, разложенной не на активную силу и реакцию связей, а на внутреннюю и внешнюю силы по

отношению ко всей системе:

Тогда принцип Даламбера для системы можно представить в другой форме:

Рис. 83

Из принципа Даламбера для системы в форме (6) или (8) можно получить следствия в виде шести условии равновесия для сил, действующих на точки системы, и сил инерции.

Если просуммировать левые части (6) по всем точкам системы, то

Умножая векторно каждое из соотношений (6) слева на радиус-вектор точки 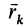и опять суммируя по точкам системы, получаем

Следствие из принципа Даламбера (10) справедливо как для неподвижной в рассматриваемой инерциальной системе отсчета точки, так и движущейся, так как начало радиусов-векторов 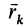можно выбирать в любой точке.

Условия (9) и (10), если выразить их через проекции на координатные оси, дадут шесть условий равновесия, аналогичных условиям равновесия сил, приложенных к твердому телу, в статике.

Если использовать принцип Даламбера в форме (8), то получим следствия в форме

так как внутренние силы системы по свойству этих сил удовлетворяют условиям

Если спроецировать (11) и (12) на координатные оси, то опять получим шесть условий равновесия для сил. Особенностью условий равновесия сил в форме (11) и (12) является отсутствие в них внутренних сил, что делает их особенно удобными при решении многих задач динамики системы.

В действительности условие (11) представляет собой теорему об изменении количества движения, а (12) — теорему об изменении кинетического момента для системы, если их представить в форме

Сравнивая (11) с (11′) и (12) с (12′), получаем формулы для вычисления главных вектора и момента сил инерции системы через количество движения и кинетический момент:

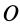
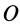
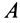
В (12′) точка неподвижна в выбранной инерциальной системе отсчета. Следовательно, по формуле (14) можно вычислить главный момент сил инерции только для неподвижной точки . Для движущейся точки вместо (12′) следует использовать ранее доказанную теорему об изменении кинетического момента для движущейся точки :

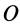
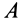
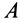
После замены в (12) точки на и сравнения с (12″) получим формулу для вычисления главного момента сил инерции относительно движущейся точки :

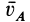
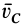
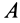
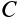
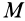
В формуле (14′) и — соответственно скорости точки и центра масс относительно рассматриваемой инерциальной системы отсчета; — масса системы.

Так как 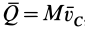, то для главного вектора сил инерции получаем формулу

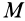
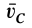
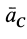
Здесь — масса системы, и — скорость и ускорение центра масс соответственно.

В тех случаях движения твердого тела, когда силы инерции приводятся к равнодействующей, последняя совпадает по модулю и направлению с главным вектором этих сил. Но равнодействующая сил инерции необязательно проходит через центр масс тела, хотя ее модуль и направление всегда определяются по формуле (15).

Проецируя векторы из (14) на ось 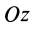, получаем

Аналогичные формулы можно получить и для других координатных осей. В случае вращения твердого тела вокруг неподвижной оси 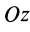, как известно,

Подставляя это значение 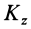в (14″), имеем

или

По формуле (16) вычисляют момент сил инерции относительно оси вращения при вращательном движении твердого тела вокруг неподвижной оси. Этот момент создают касательные силы инерции, так как нормальные силы инерции для каждой точки тела пересекают ось вращения и, следовательно, момента не создают.

Из принципа Даламбера для системы можно получить еще одно следствие — теорему об изменении кинетической энергии. Для этого умножаем (8) скалярно на 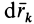и суммируем полученные соотношения по всем точкам. Получаем

или в других обозначениях

Сравнивая (17) с теоремой об изменении кинетической энергии системы в дифференциальной форме

получаем выражение для суммы элементарных работ сил инерции через кинетическую энергию системы :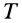

Интегрируя (18), получаем

Таким образом, сумма работ сил инерции на каком-либо перемещении системы равна изменению кинетической энергии на этом перемещении, взятому с обратным знаком.

Силы инерции твердого тела в частных случаях его движения

Методы решения задач динамики с использованием сил инерции называют кинетостатическими.

При поступательном движении

Если твердое тело движется поступательно, то ускорения его точек одинаковы. Силы инерции этих точек составляют систему параллельных сил, направленных в одну сторону. Такая система сил приводится к равнодействующей силе 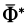, которая равна главному вектору, т. е.

Линия действия равнодействующей силы инерции в этом случае проходит через центр масс, так как главный момент сил инерции точек тела относительно центра масс

Действительно, согласно следствию из принципа Даламбера (12) для центра масс, имеем

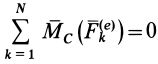
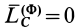
При поступательном движении тело не совершает вращения вокруг центра масс и поэтому . Следовательно, и .

При вращении вокруг неподвижной оси

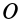
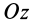
Если выбрать за центр приведения сил инерции точку на оси вращения , то в этой точке получим главный вектор и главный момент сил инерции:

Если центр масс находится на оси вращения, то 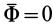. Проекции главного момента сил инерции на неподвижные оси координат в общем случае можно вычислить по формулам

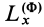
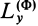
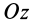
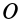
Моменты сил инерции и вычисляются в следующем параграфе. Они равны нулю, если ось  является главной осью инерции для точки .

При плоском движении

Выбрав за центр приведения сил инерции центр масс, получим в этой точке главный вектор и главный момент сил инерции. Для главного вектора сил инерции имеем

Для главного момента сил инерции относительно центра масс С, который является движущейся точкой при плоском движении тела, получим формулы, аналогичные формуле (14), выведенной для неподвижной точки .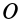

Согласно следствию из принципа Даламбера (12), главный момент сил инерции относительно центра масс удовлетворяет условию

С другой стороны, из теорем об изменении кинетического момента относительно центра масс для абсолютного и относительного движений имеем

Из этих соотношений следует

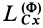
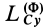
Проекции , на оси координат с началом в центре масс и движущиеся поступательно вместе с центром масс соответственно

где ось 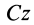перпендикулярна плоскости, параллельно которой совершают движение точки тела.

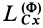
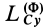
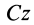
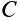
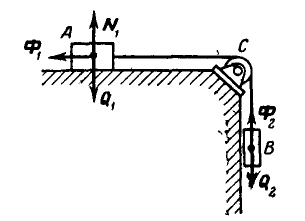
Моменты сил инерции  и  вычисляются так же, как и при вращении тела вокруг неподвижной оси. Они равны нулю, если ось является главной осью инерции для точки . Это, в частности выполняется, если тело имеет плоскость симметрии, проходящую через центр масс и параллельную плоскости движения тела.

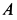
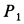
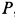
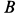
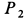
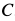
Пример 1. Груз силой тяжести опускается вниз по грани призмы с силой тяжести , приводя в движение груз , имеющий силу тяжести , с помощью нити, перекинутой через невесомый блок .

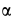
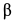
Считая пол, грани призмы и грузов гладкими, определить давление призмы на пол и выступ, препятствующий перемещению призмы, а также силу натяжения нити. Углы наклона боковых граней призмы  и (рис. 84,а,б).

Решение. Применим к системе, состоящей из призмы, грузов, нити и блока, следствия из принципа Даламбера, составив условия равновесия внешних сил и сил инерции системы.

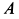
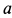
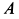
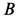
Предположим, что ускорение груза направлено вниз и равно . Для абсолютных значений сил инерции грузов и соответственно имеем

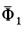
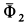
Направления сил инерции и указаны на рисунке.

Рис. 84

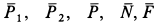
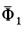
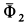
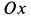
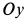
Составляя условия равновесия внешних сил системы и сил инерции и в проекциях на координатные оси , получим:

для

для

Из этих уравнений имеем а.

Для определения силы натяжения нити 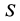и ускорения грузов применим принцип Даламбера к каждому грузу в отдельности, составив условия равновесия внешних сил грузов и сил инерции на направление нити. Получим:

для груза (рис. 84, а)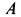

для груза 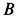(рис. 85,6)

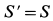
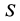
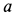
так как  для случая невесомого блока. Из (б) и (б’), исключая , определяем :

Для того чтобы груз двигался вниз, должно выполняться условие 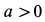или

Подставляя полученное значение 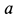в (а), получаем

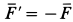
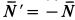
Давление призмы на выступ, согласно закону о равенстве сил действия и противодействия, будет ; давление призмы на пол .

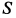
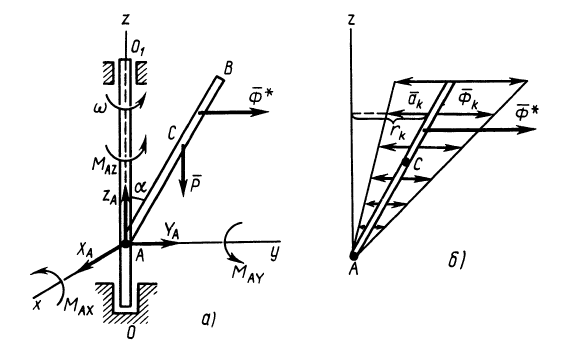
Для определения натяжения нити следует подставить значение ускорения а в одно из уравнений (б) или (б’). Тогда

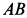
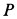
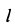
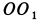
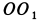
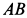
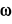
Пример 2. Однородный тонкий стержень силой тяжести и длиной жестко скреплен с вертикальным валом под углом а (рис. 85,а). Вал  вместе со стержнем  вращается с постоянной угловой скоростью .

Определить реакции стержня в заделке .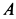

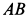
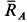
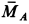
Решение. Применим к внешним силам и силам инерции стержня следствия из принципа Даламбера в форме условий равновесия сил. Неизвестные реакцию и векторный момент в заделке разложим по осям координат.

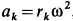
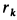
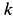
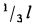
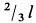
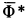
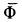
Если разбить весь стержень на элементарные участки одинаковой длины, то ускорения середин этих участков распределятся вдоль стержня по линейному закону (рис. 85,6), так как ускорение каждой точки стержня , где 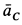— расстояние -й точки до оси вращения. Силы инерции элементарных участков стержня, принимаемых за точки, распределятся тоже по линейному закону, образуя треугольник. Распределенные так параллельные силы имеют равнодействующую силу, линия действия которой отстоит от основания треугольника на расстоянии по стержню и от вершины треугольника. Равнодействующая сила всегда равна главному вектору распределенных по треугольнику сил. Для главного вектора сил инерции имеем

где — ускорение центра масс стержня, т. е. его средней точки. Таким образом,

Рис. 85

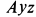
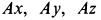
Составим шесть условий равновесия сил, приняв, что стержень в рассматриваемый момент времени находится в координатной плоскости . Тогда для проекций сил и моментов их относительно осей координат имеем:

Подставляя в эти уравнения значение 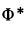и решая их относительно неизвестных, получаем:

Для силы реакции и момента в заделке имеем

Принцип Д’Аламбера

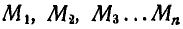
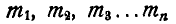
Представим себе находящуюся в движении любую несвободную систему материальных точек с массами  (рис. 302).

Рис. 302.

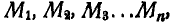
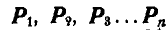
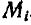
Обозначим равнодействующие задаваемых сил, приложенных к каждой точке системы  соответственно через . Рассмотрим в некоторый момент какую-либо точку системы .

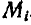
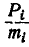
Если бы точка  не была связана с другими точками системы, то ее ускорение было бы  но при наличии связей ее с другими точками системы ускорение будет иным.

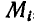
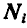
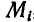
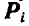
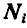
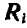
Пусть равнодействующая всех сил, с которыми остальные точки системы действуют на точку , будет сила тогда точку можно рассматривать как свободную, находящуюся под действием сил: и . Сложив эти силы по правилу параллелограмма, найдем их равнодействующую , и основное уравнение динамики запишется так:    

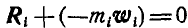
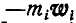
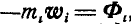
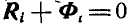
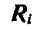
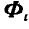
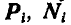
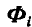
Перепишем его в форме: . Член , очевидно, имеет размерность силы. Обозначив замечаем, что последнее уравнение, переписанное в форме , является уравнением равновесия сил и , или, что то же, сил и .

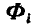
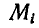
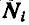
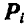
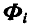
Назовем вектор силой инерции точки и тогда можем сказать, что силы, приложенные к материальной точке, и реакции связей уравновешиваются силой инерции. Или, что то же, реакция связей уравновешивается силами и .

Поступая аналогично с остальными точками системы, путем присоединения силы инерции к каждой точке, приходим к следующему началу д’Аламбера, которое читается так:

Если в какой-либо момент к движущейся системе материальных точек приложить все силы, действующие на нее в этот момент, и все силы инерции, то система будет в равновесии; при этом все реакции связей будут те же самые, которые имеют место при движении.

• Заказать решение задач по теоретической механике

Таким образом, начало д’Аламбера, изложенное в «Трактате по динамике» (1743 г.), дает очень удобный прием решения задач динамики для случаев, когда системы являются связанными, т. е. подчиненными связям. Путем присоединения к точкам системы фиктивных сил инерции задача динамики легко сводится к соответствующей задаче статики.

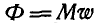
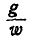
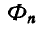
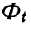
Прикладывая к точкам системы силы инерции, последние приходится при решении задач складывать по правилам статики. Особенно просто складываются силы инерции при поступательном движении твердого тела. В этом случае параллельные между собой и направленные в одну сторону силы инерции заменяются одной силой: , приложенной в центре тяжести тела, так как центр параллельных сил инерции совпадает с центром тяжести. Последнее доказывается тем, что при одновременном повороте всех сил инерции вертикально вниз и умножении их на мы получаем взамен сил инерции силы тяжести точек тела. Иногда бывает полезно силу инерции точки в криволинейном ее движении представить в виде нормальной и касательной составляющих:

направленных соответственно в сторону, противоположную нормальному и касательному ускорениям.

Примеры решения задач на принцип Даламбера

Для уяснения изложенного разберем сначала несколько задач на применение начала д’Аламбера к одной материальной точке, а затем уже к системам материальных точек.

Задача №1

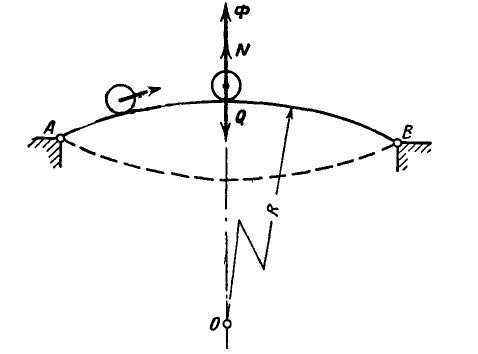
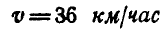
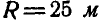
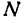
На арочный мост АВ, имеющий в точках А и В неподвижные опоры, расположенные на одной горизонтали, въезжает автомобиль весом Q = 3000 кГ с постоянной скоростью . Проезжая часть моста описана по дуге окружности радиуса . Определить наибольшие давления  и автомобиля на мост в двух случаях, когда проезжая часть моста направлена соответственно выпуклостью кверху и книзу (рис. 303).

Рис. 303.

При какой скорости 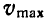автомобиля возможно его отделение от проезжей части моста?

Решение. Принимая автомобиль за материальную точку, замечаем, что для двух указанных случаев наибольшее давление автомобиля на мост будет тогда, когда он находится соответственно в наивысшей и наинизшей точках проезжей части, так как в этом случав все силы, приложенные к автомобилю, направлены по одной прямой.

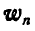
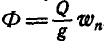
Для нахождения давления автомобиля на мост в первом случае применяем начало д’Аламбера, для чего к силам, действующим на автомобиль, а именно к его весу Q и нормальной реакции моста N, присоединяем силу инерции Ф, направленную в сторону, обратную ускорению автомобиля  и равную . Так как теперь мы имеем уже дело с задачей статики, то составляем уравнение равновесия сил Q, N и Ф  в виде равенства нулю суммы их проекций на вертикальное направление:

откуда

С такой же силой автомобиль будет оказывать давление на мост. Если выпуклость моста направлена книзу, то при решении задачи по началу д’Аламбера надо силу инерции Ф в этом случае направить уже вниз, так как ускорение автомобиля направлено вверх.

Обозначив для рассматриваемого случая нормальную реакцию моста через 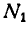, найдем:

или

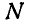
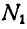
Сравнивая величины  и  замечаем, что во втором случае давление автомобиля на мост значительно больше, чем в первом.

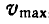
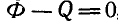
Полагая в первом уравнении N=0, найдем наибольшую скорость , при которой возможно отделение автомобиля от проезжей части моста: , или

откуда

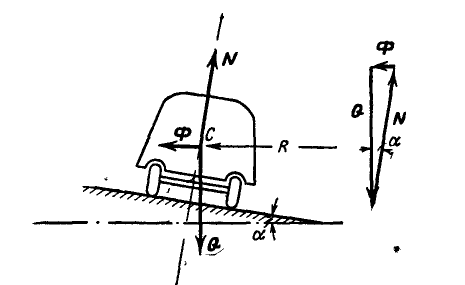
Задача №2

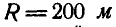
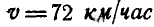
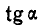
Автомобиль движется по криволинейному участку дороги радиусом со скоростью. Каков должен быть поперечный уклон полотна дороги, характеризуемый (где — угол наклона полотна дороги к горизонту), для того чтобы давление движущегося автомобиля было направлено перпендикулярно к полотну дороги.   

Рис. 304.

Решение. Рассматривая автомобиль как материальную точку, приложим к центру тяжести его С силу инерции Ф, равную 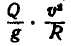и направленную в сторону, противоположную нормальному ускорению точки С (рис. 304). Теперь три силы, приложенные к точке С — вес автомобиля Q, нормальная реакция дороги N и сила инерции Ф, согласно началу д’Аламбера, взаимно уравновешиваются, поэтому треугольник этих сил должен быть замкнут.

Построив этот треугольник, находим:

Задача №3

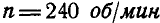
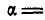
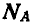
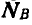
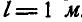
Вал АВ, соединенный жестко со стержнем CD, вращается, делая . К концам стержня CD, наклоненного под углом 45° к валу АВ, прикреплены два одинаковых груза весом Q = 50 кГ каждый (рис. 306). Найти реакции и подшипников А и В при .

Рис. 306.

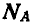
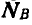
Решение. Для нахождения реакций подшипников и применим начало д’Аламбера, для чего к каждому из грузов С и D присоединим силу инерции Ф, равную

Теперь вал АВ вместе с прикрепленным к нему стержнем CD и грузами находится в равновесии под действием сил тяжести грузов, реакций подшипников и фиктивных сил инерции.

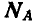
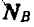
Неизвестные реакции и определим теперь хотя бы из следующих двух уравнений равновесия:    

откуда

Задача №4

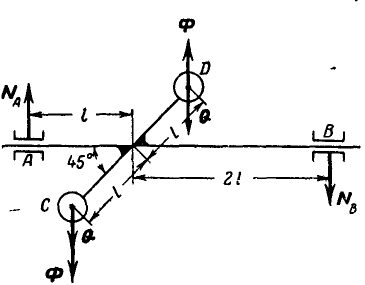
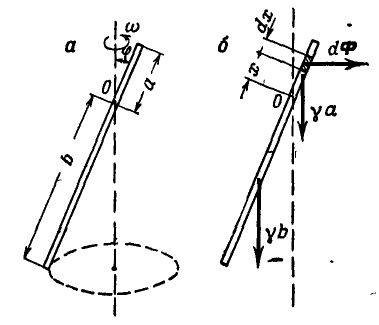
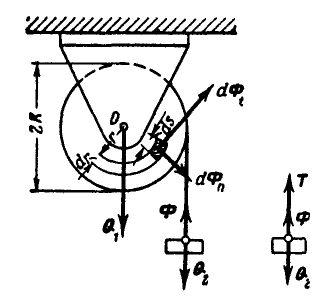
Однородный стержень вращается вокруг вертикальной оси с постоянной угловой скоростью 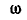(рис. 307, а). Размеры стержня указаны на чертеже. Найти установившийся угол , образованный между стержнем и его вертикальной осью вращения.

Рис. 307.

Решение. Разобьем весь стержень на ряд элементарных отрезков длиной dx каждый (рис. 307, б); тогда элементарная сила инерции, приходящаяся на выделенный элемент, будет:

где 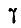— вес единицы длины стержня.

Момент элементарной силы инерции относительно точки О будет:

Так как после присоединения сил инерции стержень будет находиться в равновесии, то для. определения угла 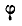составим уравнение равновесия в форме равенства нулю суммы моментов всех сил тяжести и сил инерции относительно точки О:

откуда

Задача №5

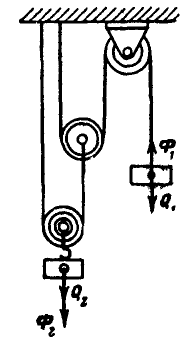
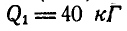
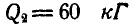
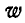
На блок с неподвижной осью вращения, представляющий однородный диск радиусом R и весом , намотан канат, к концу которого подвешен груз весом (рис. 308). Найти ускорение груза и натяжение каната, если груз будет предоставлен самому себе. Массой каната пренебречь.

Рис. 308.

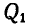
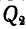
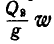
Решение. Для решения задачи воспользуемся началом д’Аламбера. Заданными силами, действующими на систему, состоящую из груза и блока, являются веса и . Так как ускорение груза направлено вниз, то его сила инерции направлена вверх и равна .

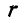
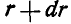
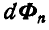
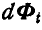
Для вычисления сил инерции блока выделим элемент, ограниченный радиусами и и дугой ds;  тогда сила инерции этого элемента может быть представлена в виде двух составляющих — нормальной и касательной причем:

где 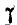— вес единицы площади блока.

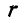
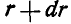
Найдем теперь момент относительно оси вращения О всех сил инерции, приходящихся на элементарное кольцо, ограниченное окружностями радиусов и ; он равен:

Сюда вошел момент только касательных сил ннерцни; момент же нормальных сил инерции блока относительно точки О обращается в нуль.

Так как после присоединения сил инерции ко всем точкам системы последняя находится в равновесии, то для определения ускорения груза 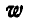приравниваем нулю сумму моментов всех заданных сил н сил инерции системы относительно оси вращения О:

Имея в виду равенства:

найдем окончательно:

Чтобы определить натяжение Т каната, воспользуемся следующим приемом: разорвем канат и взамен этого введем его реакцию, равную Т. Тогда, рассматривая отдельно равновесие груза 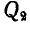(рис. 308 справа), найдем:

откуда

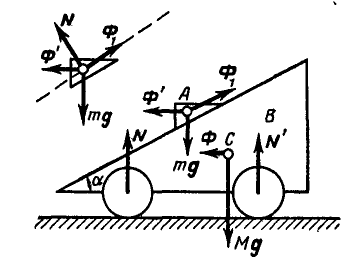
Задача №6

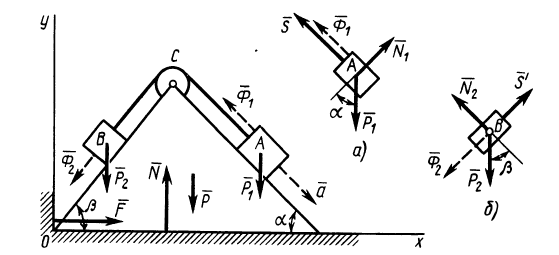
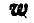
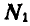
По установленной на рельсах платформе В, представляющей наклонную плоскость, перемещается под влиянием силы тяжести груз А, который можно считать за материальную точку (рис. 310). При движении груза по платформе, последняя будет перемещаться вправо. Пренебрегая силами трения, определить ускорение  платформы, а также давление груза на платформу, если масса груза равна т, а масса платформы М.

Решение. Заданная нам система состоит из груза А, при; нятого нами за материальную точку, и платформы В, движущейся поступательно. Применим принцип д’Аламбера, для чего приложим ко всем точкам системы силы инерции.

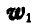
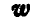
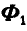
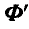
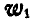
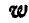
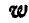
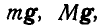
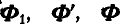
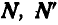
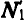
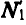
Так как точка А совершает сложное движение и ее ускорение складывается из относительного , направленного вниз параллельно наклонной плоскости, и переносного , равного ускорению платформы, то и сила инерции точки А состоит из двух компонентов:  и , направленных прямо противоположно ускорениям и . Сила ннерции Ф платформы приложена в ее центре тяжести С и направлена в противоположную сторону ускорению . Теперь уже система находится в равновесии под действием заданных сил сил инерции  и реакций рельсов (сила давления груза на платформу и реакция платформы взаимно уравновешиваются).

Рис. 310.  

Напишем уравнение равновесия сил, приложенных к системе, в форме равенства нулю проекций нх на ось, совпадающую с направлением рельсов:

или

 

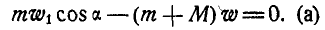
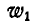
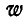
Это уравнение содержит два неизвестных  и . Составим второе уравнение, исходя из рассмотрения равновесия точки А, для чего приравняем нулю сумму проекций всех сил, приложенных к точке А, на ось, параллельную наклонной плоскости (рис. 310, вверху):

или

После сокращения на 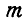получим:

Из уравнений (а) и (б) определяем

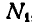
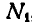
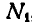
Давление груза на платформу равно реакции плоскости но противоположно по направлению. Для нахождения составим равенство нулю суммы проекций всех сил, приложенных к точке А, на направление оси, совпадающей с направлением .

откуда

Переходя к изучению движения любой системы материальных точек, мы применим принцип виртуальных перемещений, включив, согласно началу д’Аламбера, в число приложеных сил — силы инерции.

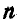
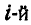
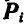
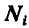
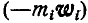
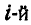
Пусть движущаяся система состоит из материальных точек и подчинена двусторонним и идеальным связям. Обозначим равнодействующую всех задаваемых сил, приложенных к точке через , а равнодействующую реакций связей — через ; тогда, введя силу инерции , запишем уравнение, выражающее принцип возможных перемещений для точки:

а для всей системы:

или

В силу идеальности связей сумма работ их реакций на возможном перемещении системы обращается в нуль:

Отсюда прнходим к общему уравнению динамики, выраженному в векторной форме:

или в проекциях:

       

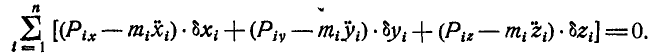
Это и есть общее уравнение динамики, или уравнение д’ Аламбера — Лагранжа, выражающее начало д’Аламбера в аналитической форме. Из него можно вывести уравнения равновесия и движения любых материальных систем.  

Применение этого уравнения выясним на отдельных задачах.    

Задача №7

Груз А весом 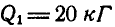находится на горизонтальной гладкой плоскости и скреплен с нитью, перекинутой в точке С через малый блок, массой которого пренебрегаем (рис. 311).

К концу нити подвешен свободно груз В весом 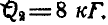Найти ускорение груза В  и натяжение нити Т.

Рис. 311.

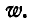
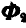
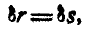
Решение. Пусть грузы А и В движутся с ускорением Остановим систему и приложим к грузам А и В силы инерции и . Дадим теперь системе возможное перемещение  переместив грузы, хотя бы слева направо, и составим уравнение работ:

или

откуда

Натяжение нити Т легко определится, если нить оборвать и рассмотреть равновесие одного из грузов, например В. Тогда, приравнивая нулю сумму проекций всех сил, приложенных к В на вертикальное направление, найдем:

или

Задача №8

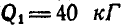
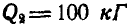
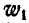
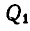
К системе блоков (рис. 312) подвешены грузы:  и  . Пренебрегая массами блоков, определить ускорение груза и натяжение нити Т.

Рис. 312.

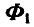
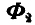
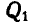
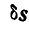
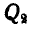
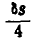
Решение. Приложим к грузам силы инерции и и дадим системе возможное перемещение. Если груз опустим вниз на величину , то груз поднимется вверх на .

Отсюда следует, что ускорение второго груза будет также в четыре раза меньше ускорения первого груза.

Напишем теперь уравнение работ:

или

откуда

Натяжение нити T найдем из рассмотрения равновесия, например, первого груза:

или

Задача №9

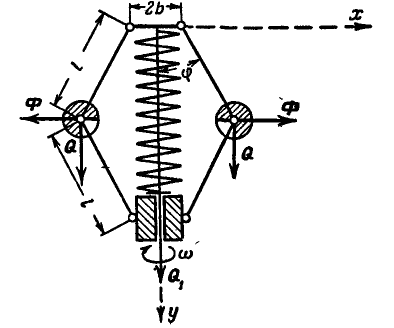
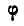
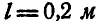
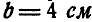
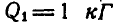
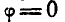
Найти, при каком числе оборотов в минуту регулятора вокруг вертикальной оси угол отклонения его плеч от вертикали будет равен 45° (рис. 313). Данные величины: длина плеч регулятора , расстояние от оси вращения до шарнира , вес каждого из шаров Q = 2 кГ, жесткость пружины с= 10 кГ/см, вес муфты  и при пружина не растянута и не сжата.

Рис. 313.

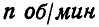
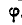
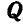
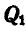
Решение. Пусть при угол отклонения плеч регулятора от вертикали равен . При этом на систему, состоящую из двух шаров и муфты, действуют следующие заданные силы: веса шаров , вес муфты , а также сила упругости пружины Р:

Все эти силы направлены по вертикали вниз.

Решим задачу, пользуясь началом д’Аламбера, для чего приложим к шарам равные по величине силы инерции:

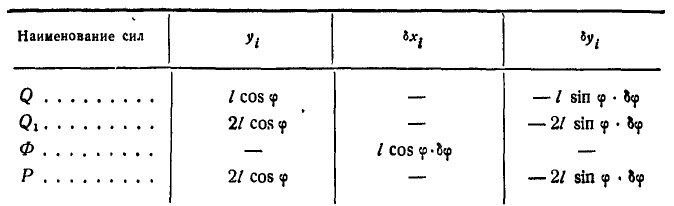
При составлении уравнения работ все вычисления сведем в таблицу 13. В таблицу 13 введены силы и , приложенные к шару, находящемуся справа от оси вращения.

Таблица 13

Отсюда

или   

Но так как , то