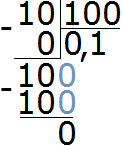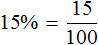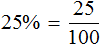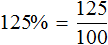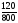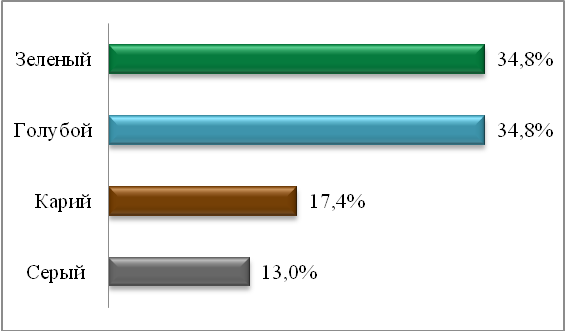Автор: Пушкова Раиса Егоровна
Должность: учитель математики
Учебное заведение: МБОУ СОШ № 51 г.Брянска
Населённый пункт: Брянская область г.Брянск
Наименование материала: Проект ученика 6 класса
Тема: «Проценты в математике и в нашей жизни»
Раздел: среднее образование
МБОУ СОШ № 51
Проект
по математике
на тему:
Проценты в математике и в нашей жизни
Выполнил: Татаринов А. А.
ученик 6 б класса
Проверила: Пушкова Р.Е.
г. Брянск
2016
1
Содержание
Введение…………………………………………………………….. 3
Цели и задачи проекта……………………………………………… 4
1.
Процент. Основные понятия…………………………………. 5
2.
Происхождение процентов…………………………………… 6
3.
Проценты в нашей жизни…………………………………….. 8
4.
Задачи на проценты. И способы их решения………………… 9
5.
Ребусы, стихи, загадки про проценты………………………. 12
Заключение………………………………………………………….. 15
2
Введение
Тема моего проекта «Проценты в математике и в нашей жизни». Я выбрал
эту
тему,
потому
что,
будучи
совсем
маленьким
и
постоянно
слыша
от
взрослых такие фразы как: « 30 % скидки», «подорожает на 20 %» и тому
подобные. Уже тогда мне было интересно, что же такое «Процент». А после
знакомства на уроках математики с процентами, мне захотелось узнать о них
еще больше. Для чего мы их изучаем, где можно применить полученные
знания, как часто приходится сталкиваться с процентами? Нужны ли будут
нам в жизни проценты?
3
Цели и задачи проекта
Цели проекта:
1.
Понять, что такое процент;
2.
Расширить знания о проценте;
3.
Выяснить, где и как проценты применяются в нашей жизни.
Задачи проекта:
1.
Изучить историю происхождения процента;
2.
Рассмотреть задачи на проценты
;
3.
Определить сферу практического применения процента.
4
Процент. Основные понятия.
Проце́
нт
(от латинского слова pro centum, что буквально означает «за
сотню»
или
«со
ста») —
одна
сотая
часть.
Обозначается
знаком
«%».
Используется
для
обозначения
доли
чего-либо
по
отношению
к
целому.
Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть 85 кг.
Справедливо
также
утверждение,
что
200 %
от
500 кг
является
1000 кг,
поскольку 1 % от 500 кг равен 5 кг, и 5 ∙ 200 = 1000.
5
Происхождение процентов.
Идея выражения частей целого постоянно в одних и тех же долях,
вызванная
практическими
соображениями,
родилась
еще
в
древности
у
вавилонян,
которые
пользовались
шестидесятеричными
дробями.
Уже
в
клинописных таблицах вавилонян содержатся задачи на расчет процентов. До
нас
дошли
составленные
вавилонянами
таблицы
процентов,
которые
позволяли быстро определить сумму процентных денег.
Были известны проценты и в Индии. Индийские математики вычисляли
проценты,
применив
так
называемое
тройное
правило,
т.
е.
пользуясь
пропорцией.
Они
умели
производить
и
более
сложные
вычисления
с
применением процентов.
Денежные расчеты с процентами были особенно распространены в
Древнем
Риме.
Римляне
называли
процентами
деньги,
которые
платил
должник заимодавцу за каждую сотню. Даже римский сенат вынужден был
установить максимально допустимый процент, взимаемый с должника, так
как некоторые заимодавцы усердствовали в получении процентных денег. От
римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особо
много
внимания
обращали
на
умение
вычислять
проценты.
В
то
время
приходилось рассчитывать не только проценты, но и проценты с процентов, т.
е. сложные проценты, как называют их в наше время. Отдельные конторы и
предприятия
для
облегчения
труда
при
вычислениях
процентов
разрабатывали
свои
особые
таблицы,
которые
составляли
коммерческий
секрет фирмы.
Впервые опубликовал таблицы для расчета процентов в 1584 году Симон
Стевин
–
инженер
из
города
Брюгге
(Нидерланды).
Стевин
известен
замечательным
разнообразием
научных
открытий
в
том
числе
–
особой
записи десятичных дробей.
6
Употребление термина «процент» в России начинается в конце 18 в.
Долгое время под процентами понимались исключительно прибыль и убыток
на каждые 100 рублей. Они применялись только в торговых и денежных
сделках. Затем область их применения расширилась, проценты встречаются в
хозяйственных и финансовых расчетах, статистике, науке и технике. Нынче
процент
–
это
частный
вид
десятичных
дробей,
сотая
доля
целого
(принимаемого за единицу).
Знак % происходит, как полагают, от итальянского слова cento (сто),
которое
в
процентных
расчетах
часто
писалось
сокращенно
cto.
Отсюда
путем дальнейшего упрощения в скорописи буквы t в наклонную черту
произошел современный символ для обозначения процента.
Существует и другая версия возникновения этого знака. Предполагается,
что
этот
знак
произошел
в
результате
нелепой
опечатки,
совершенной
наборщиком. В 1685 году в Париже была опубликована книга – руководство
по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал
%.
7
Проценты в нашей жизни.
Проценты – одно из математических понятий, которые часто встречаются
в повседневной жизни. Так, мы часто читаем или слышим, что например, в
выборах приняли участи 52,5% избирателей, рейтинг победителя хит-парада
равен
75%,
промышленное
производство
сократилось
на
11,3%,
уровень
инфляции 8% в год, банк начисляет 12% годовых, молоко содержит 3,2%
жира, материал содержит 60% хлопка и 40% полиэстера и т.д.
8
Задачи на проценты. И способы их решения.
Основные задачи на проценты можно разделить на три группы:
1. Нахождение процентов от числа.
Правило: Чтобы найти проценты от числа, нужно сначала найти один
процент, а потом умножить полученное число на количество процентов.
Пример: В бензобаке автомашины было 60 л. бензина. На поездку
израсходовали 25% этого бензина. Сколько литров бензина израсходовали на
поездку?
1 способ
Решение:
1) 60 : 100 = 60/100
(л)- составляет 1%.
2)60/100 *25=15(л)- израсходовали на поездку.
Ответ: 15 л. бензина израсходовали.
2 способ
Решение:
1)
100-25=75% — осталось бензина.
2)
75/100*60=45 (л) – бензина осталось.
3)
60-45=15 (л)- бензина израсходовали.
Ответ: 15 л. бензина израсходовали.
3 способ
Решение:
1)
25%=25/100=1/4 – бензина израсходовали.
2)
60*1/4=15 (л) – бензина израсходовали.
Ответ: 15 л. бензина израсходовали.
4 способ
Решение:
60 л. – 100 %
Х л. – 25 %
Составляем пропорцию
Х= 60*25/100=15 (л) – бензина израсходовали.
Ответ: 15 л. бензина израсходовали.
2. Нахождение числа по его проценту.
Правило:
Чтобы найти число по его проценту, нужно сначала найти один
процент, а потом умножить полученное число на 100 процентов.
Пример: Заасфальтировав 40 км дороги, ремонтники тем самым выполнили
20% плана. Сколько километров дороги надо заасфальтировать по плану?
1 способ
Решение:
1)40:20=2(км) — составляет 1%.
9
2) 2*100%=200(км) — надо заасфальтировать по плану.
Ответ: 200км.
2 способ
Решение:
40 км. – 20 %
Х км. – 100 %
Составляем пропорцию
Х=40*100/20=200 (км) — надо заасфальтировать по плану.
Ответ: 200 км.
3 способ
Решение:
1)
20%=20/100=1/5 – выполнено по плану.
2)
Примем за 1 – весь план, тогда
40 км – 1/5
Х км – 1
Составляем пропорцию
Х=(40*1)/(1/5)=200 (км) — надо заасфальтировать по плану.
Ответ: 200 км.
3.Нахождение процентного отношения чисел:
Правило:
Чтобы найти процентное отношение чисел надо отношение этих
чисел умножить на 100%.
Пример: Мама купила 650 грамм конфет. За вечер съели 260 грамм конфет.
Сколько процентов имеющихся конфет съели за вечер?
1 способ
Решение:
1)
260/650=0,4
2)
0,4*100=40%
Ответ: 40% конфет съели.
2 способ
Решение:
1)
650-260=390 (г) – конфет осталось.
2)
390/650*100=60% — конфет осталось.
3)
100-60=40% — конфет съели.
Ответ: 40% конфет съели.
Алгоритм решения задач
10
1.
Прежде,
чем
начать
решать
подобные
задачи,
необходимо
повторить методы отыскания части от целого и целого по части.
2.
Выяснить, какая величина принята за целое, т.е. за 100%.
3.
Ответить на вопрос: известна ли эта величина?
4.
Выяснить, как найти величину, которая приходится на 1%.
5.
Выяснить,
что
требуется
найти
–
число
по
его
проценту
или
процент от числа.
6.
Выполнить
необходимые
действия.
Ребусы, стихи, загадки про проценты
11
Проценты.
В математике есть термин,
Именуется «процент».
Мы вам с точностью ответим:
Проще ничего и нет.
Это, кто ещё не знает,
Одна сотая числа.
Кто процент легко считает,
Тот повсюду голова.
Измеряются в них скидки,
Что торговцы нам дают,
Вклады в банках и кредиты,
И инфляция валют.
Если в классе все чихают,
Есть большой процент больных, —
Карантин пообещают,
12
От учёбы передых.
Как маткласс, мы твёрдо скажем:
Знать процент – большая честь.
Без процентов не дано нам
Ни дышать, ни пить, ни есть.
И конечно, пожелаем
Вам, и нам, и всем подряд,
Чтоб в учёбе был достигнут
Стопроцентный результат!
Загадки
Я знаю только 1)
на рубль -копейки
на доллары-центы
бегут- набегают в банке…..
(Проценты)
13
Заключение
Изучение процента продиктовано самой жизнью.
Без понятия «процент»
нельзя обойтись.
Они нас окружают почти везде. Люди многих профессий
работают
с
процентами.
Например,
экономисты,
бухгалтера,
банкиры,
продавцы. Чтобы
начислить
зарплату
работнику,
нужно
знать
процент
налоговых отчислений; чтобы открыть счет в сбербанке, наши родители
интересуются размером процентных начислений на сумму вклада. Именно в
торговле понятие «процент» используется наиболее часто: мы очень часто
слышим о скидках, наценках, уценках, и т.д. — все это проценты.
Умение
выполнять процентные вычисления и расчеты необходимо каждому человеку,
так как с процентами мы сталкиваемся в повседневной жизни.
14
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь
в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
2% = = 0,02
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
Найти от 10 см
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
0,1 × 2 = 0,2
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
0,2 см = 2 мм
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
300 : 100 = 3
Теперь полученный результат умножаем на 50
3 × 50 = 150 руб.
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти
от 300 рублей, а решать такие задачи для нас пока проще
300 : 100 = 3
3 × 50 = 150
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
1200 : 100 = 12
12 × 32 = 384
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись , а если перевести эти
в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
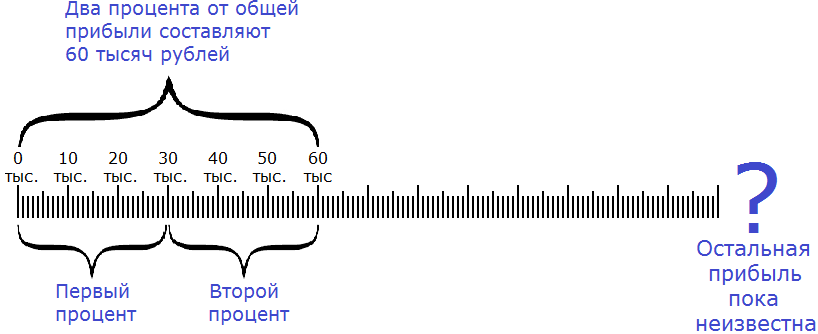
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35 : 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500 : 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35 : 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Задания для самостоятельного решения
Задание 1. Найдите 20% от числа 200
200 : 100 = 2
2 × 20 = 40
Задание 2. Найдите 34% от числа 1050
1050 : 100 = 10,5
10,5 × 34 = 357
Задание 3. Найдите 25% от числа 80
80 : 100 = 0,80
0,8 × 25 = 20
Задание 4. Найдите 185% от числа 1,5
1,5 : 100 = 0,015
0,015 × 185 = 2,775
Задание 5. Найдите 150% от числа 1150
1150 : 100 = 11,50
11,50 × 150 = 1725
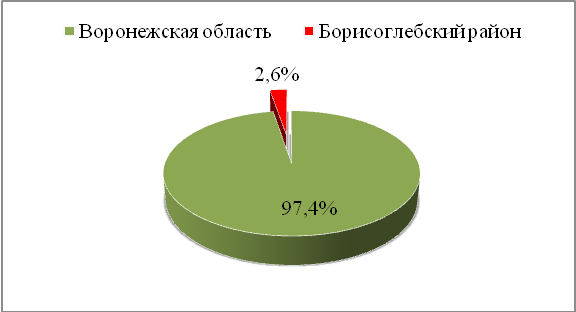
Задание 6. Представьте выражение 15% в виде обыкновенной дроби
Задание 7. Представьте выражение 25% в виде обыкновенной дроби
Задание 8. Представьте выражение 125% в виде обыкновенной дроби
Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.
12 : 60 = 0,2
0,2 × 100 = 20
Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.
40 : 20 = 2
2 × 100 = 200
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Министерство образования и науки Российской Федерации
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 4 рп Ванино Ванинского муниципального района Хабаровского края
Задачи на проценты в жизни человека
(исследовательская работа)
Выполнили: Семчук Назар и
Зоткина Валерия,
учащиеся 6 А класса
МБОУ СОШ № 4
рп Ванино
Руководитель: Гусятникова М.Д.,
учитель математики
рп Ванино
2015 г
Содержание
| Раздел | Наименование | Страницы |
| Раздел 1. | 1.1Актуальность 1.2.Проблема 1.3.Объект исследования 1.4.Предмет исследования 1.5.Гипотеза 1.6.Цель работы 1.7.Задачи работы 1.8.Методы исследования 1.9.Новизна исследования | 2 – 3 стр. |
| Раздел 2. | 2.1.История возникновения процента 2.2.Решение задач 2.3.Проценты в жизни человека | 3 — 4 стр. 4 -7 стр 5 — 7 стр. |
| Раздел 3. | Заключение | 7 стр. |
| Раздел 4. | Список используемой литературы | 7 стр. |
| Раздел 5. | Приложения | 8 стр. |
Раздел 1.
-
Актуальность. На уроках математики мы познакомились с процентами. Узнали, что проценты – одно из математических понятий, которые часто встречаются в повседневной жизни. Нам стало интересно узнать, когда люди впервые узнали о процентах, как они использовали проценты для решения практических задач, а также заинтересовались вопросом, часто ли мы можем встретить проценты в жизни и в быту.
-
Проблема: Люди часто в повседневной жизни сталкиваются с процентами, но не могут решать задачи на проценты.
-
Объект исследования: процент как универсальная единица сравнения различных данных
-
Предмет исследования: практические задачи на проценты
-
Гипотеза: удобно ли сравнивать с помощью процентов данные с разными параметрами
-
Цель работы: .определить процент как единицу сравнения данных с разными параметрами и доказать необходимость использования процентных соотношений
-
Задачи:
-
Изучить историю происхождения процента;
-
Рассмотреть задачи практического применения «процента»;
-
Исследовать возможности применения «процента».
-
Методы исследования: сбор и изучение информации, определение проблем при решении задач способом опроса.
-
Новизна исследования: ранее работа в данном направлении в МБОУ СОШ № 4 рп Ванино не проводилась.
Раздел 2.
2.1. История возникновения процента
Слово «процент» происходит от латинского «pro centum», что означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях.
Это дает возможность упрощать расчеты и сравнивать части между собой и целыми. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян.
Уже в клинописных табличках вавилонян содержатся задачи на расчет процентов. (Приложение 1.)
Проценты были известны еще в индии в V веке. Именно в Индии с давних пор счет ведется в десятичной системе счисления.
Индийские математики применяли для вычисления процентов так называемое тройное правило, то есть пользовались пропорцией.
Особенно распространены проценты были в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.
Есть мнение, что понятие «процент» ввел бельгийский ученый Симон Стевин. В 1584 году он опубликовал таблицы процентов.
Употребление термина «процент» в России начинается в конце XVIII в.
Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако, наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.
2.2. Решение задач
Рассмотрим виды задач, решаемые в школе. Покажем практическое применение данных задач.
Мы изучаем три вида задач на проценты:
-
Нахождение процента от числа
-
Нахождение числа по его проценту
-
Нахождение процентного отношения двух чисел
Задача 1. Нахождение процента от числа.
В библиотеку школы поступило 1000 новых учебников. 40 % из них для учащихся начальной школы. Сколько учебников поступило в библиотеку для учащихся начальной школы?
Решение: Сначала выразим 40 % обыкновенной и десятичной дробью. 40 % =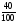

Ответ: 400 учебников.
Задача 2. Нахождение числа по его проценту.
По итогам второй четверти в нашем классе 12 хорошистов, что составляет
40 % от числа всех учащихся класса. Сколько учащихся в классе?
Решение: Итак, нам неизвестно сколько всего учащихся в классе. Но мы знаем, что хорошисты составляют 40 % от общего количества учащихся класса. Нужно 12 разделить на дробь 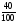
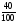
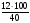
Ответ: 30 учеников в классе.
Задача 3. Нахождение процентного отношения двух чисел.
Из 800 учеников нашей школы 120 занимается в хоккейном клубе «Трансбункер». Сколько процентов всех учеников школы занимаются в хоккейном клубе «Трансбункер»?
Решение : нам нужно найти количество хоккеистов. Для этого нужно неизвестную часть (120 хоккеистов) разделить на общее количество учеников школы (800 учеников) и умножить на 100 %, т.е. 
Ответ: 15 % учащихся школы занимаются хоккеем.
2.3. Проценты в жизни человека
Услышав о процентах в первый раз, мы вдруг заметили, что проценты окружают нас повсюду. Мы работаем с процентами на уроках в школе (математики, физики, химии, биологии, географии и др.), при составлении отчетов работниками администрации школы, учителями, библиотекарями. Работники торговли либо делают наценку на товар, либо объявляют скидки, выражая величины в процентах. Работодатели повышают или понижают зарплату, оперируя понятием процента. В банках, СМИ, медицине, интернете и других сферах.
Научившись решать задачи на проценты, мы решили составить задачи практического содержания. Провели наблюдения и составили диаграммы.
-
Диаграмма прогноза погоды в Ванино в апреле 2015 г.
Мы наблюдали за погодой в течении одного месяца, вели дневник наблюдений и выяснили, что солнечная погода была 18 дней, что составило 60% от общего количества дней в апреле 2015 г; плохую погоду мы наблюдали в течении 5 дней – 17%, погоду с переменной облачностью мы увидели 7 дней – 23 %.
-
Диаграмма численности населения
Затем мы сравнили численность населения п. Ванино, п. Октябрьский, п. Токи. (Данные взяли на сайтах поселков). Из диаграммы наглядно видно, что в п. Ванино проживает людей больше, чем в п. Токи и п. Октябрьский.
Таблица результатов
| 2013г | 2014г | 2015г | |
| п. Ванино | 16496 | 16076 | 15756 |
| п. Токи | 2394 | 2327 | 2317 |
| п. Октябрьский | 6093 | 6040 | 6013 |
| Всего в Ванинском районе | 36115 | 35291 | 34873 |
Далее мы подсчитали процентное отношение жителей каждого поселка в 2015 году ко всем жителям района. Получили, что в п. Ванино проживает 45 % населения Ванинского района, в п. Токи – 6 %,
в п. Октябрьский – 17 %.
-
Мы сравнили цены на продукты в п. Ванино и в г. Хабаровске и сделали вывод, что в нашем поселке продукты стоят дороже.
Хлеб в г.Хабаровске стоит 16,5 руб (21 %), в Ванино – 25 руб (31%). Сахар в г.Хабаровске стоит 58 руб (72,5 %), в Ванино – 80 руб (100%). Яйцо в г. Хабаровске стоит 49 руб (61%), в Ванино – 76 руб (95 %).
-
Мы обратились к работникам банка и выяснили, что одним из самых наглядных примеров применения процентов в жизни является процент по кредиту. (Кредит – отпускаемая на что-нибудь денежная сумма. Толковый словарь Ожегова).
Процентная ставка – сумма, указанная в процентном выражении к сумме кредита, которую платит получатель кредита за пользование им в расчете на определенный период. То есть, если мы возьмем 100000руб на 1 год под 20 %, то мы должны будем ежемесячно выплачивать по 9263 руб, а переплата за кредит составит 11161 руб.
-
Мы заметили проценты на одежде. Покупая вещи, надо обращать внимание на состав одежды. Особенно тем людям, которые страдают аллергией на какие-то волокна. Например, если у вас аллергия на шерсть, надо смотреть процентное содержание шерсти в составе одежды.
-
У всех молочных продуктов есть своя массовая доля жира, обозначающая процент жирности продукта. Чем жирнее продукт, тем он калорийней. Например, молоко (3,2 %), майонез (60 %), кефир (2,5 %), молоко сгущенное (8,5 %) и т.д.
-
При закатывании банок на зиму хозяйки добавляют продукты в процентном отношении. Например, надо знать, сколько положить уксуса при 9% или 70 %. Это важно.
Раздел 3.
Заключение
Проанализировав нашу исследовательскую работу на тему «Задачи на проценты в жизни человека» мы поняли, что проценты играют важную роль в нашей повседневной жизни. Мы сделали вывод: без понимания сущности процента жизнь современного человека будет крайне сложной.
В результате проведенной исследовательской работы мы изучили историю происхождения процентов, рассмотрели основные задачи практического применения процентов, исследовали возможность применения процентов в повседневной жизни человека.
Раздел 4.
Использовались интернет — источники по теме исследовательского проекта.
Раздел 5.
Диаграммы из Приложения опубликованы в тексте исследовательской работы.
Приложение 1.
7
Проект
«Проценты в нашей жизни» приготовили: учащиеся 6 кл «СОШ№3»Клёпов А, Сукманов А. руководитель: Дремухина Т.А
Выяснить, где и как проценты применяются в нашей жизни. Расширить знания о применении процентных вычислений в задачах и в разных сферах жизни человека.
Цель:
- Провести исследования и с помощью процентных вычислений представить данные в виде задач и диаграмм
Задачи проекта:
- Изучить историю происхождения процента;
- Рассмотреть задачи на проценты из практической жизни и окружающей среды современного человека.
Актуальность нашего проекта
Проценты — это одна из сложнейших тем математики, и очень многие учащиеся затрудняются или вообще не умеют решать задачи на проценты. А понимание процентов и умение производить процентные расчёты необходимы для каждого человека. Прикладное значение этой темы очень велико и затрагивает финансовую, экономическую, демографическую и другие сферы нашей жизни. Изучение процента продиктовано самой жизнью. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни.
План наших действий
- Мы изучили дополнительно тему проценты их историю
- Выяснили что знают родители, родственники
- Составили свои задачи на проценты
- Решили некоторые задачи из ЕГЭ
- Приготовили презентацию
Немного из истории
Слово «процент» имеет латинское происхождение: «pro centum» — «со ста». Часто вместо слова «процент» используют словосочетание «сотая часть числа».Процентом называется сотая часть числа. 1/100=1%Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник (заимодавцу) за каждую сотню.
Так как слова «на сотню» звучали как «процентум», то сотую часть стали называть процентом
Символ появился не сразу. Сначала писали слово «сто» так:
В 1685г. в Париже была напечатана книга «Руководство по коммерческой арифметике», где по ошибке вместо было набрано .
От римлян проценты перешли к другим народам Европы. В Россию понятие процент ввел Пётр I.
2.Проценты в нашей жизни.
Проценты — одно из математических понятий, которое часто встречаются в повседневной жизни. Мы слышали например, что
В магазине скидка 20%
в выборах приняли участие 57% избирателей,
успеваемость в классе 100%,
банк начисляет 16% годовых,
Уксусная кислота 70%
материал содержит 100% хлопка и т.д
Пацан 100%- В разговоре означает лучший во всем!
Три основные действия, связанные с процентами
1. Нахождение процентов от числа.
Чтобы найти у% от в, надо в·0,01.
2. Нахождение числа по его процентам.
Если известно, что у% числа x равно в, то x=в:0,01.
3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100%.
Проценты применяются
1. в медицине
2. в программировании
3. в магазинах
4. на выборах
5. в кулинарии
6. в статистике
7. в составах тканей
8. в налогах
9. в растворах
10. в сбербанках
11. в анализе деятельности
Проценты используют люди разных профессий
Проведя исследования в нашем классе мы собрали некоторые данные и обработав их мы получили такие результаты
Дни рождения в классе по временам года
От школьного бухгалтера мы узнали, что
- Ежемесячно от зарплаты работников, работодателем отчисляется:
- — в Пенсионный фонд — 22 %;
- — фонд социального страхования – 2,9%;
- — фонд соц. страхования от несчастных случаев – 0,2%
- — фонд регионального медицинского страхования – 5,9%. Итого 30,2%
- Налог отчисляемый от зарплаты работника НДФЛ =13%
- Например зарплата составляет 14500рублей -13% НДФЛ =14500-1885=12615руб получит работник на руки
Вот такие задачи мы составили опираясь на полученные сведения
Лесные угодья г.Северобайкальска занимают площадь 1651527 км2. Летом наш город был долгое время весь в дыму, горел лес. Сколько процентов леса сгорело во время Пожара, если площадь пожара 25234кв.км(1,5%)
История нашего города
- Мы провели опрос среди жителей г. Северобайкальск «Знаете ли вы герб нашего города» из 123 опрошенных 65% людей знают герб, остальные нет. Сколько человек из опрошенных не знает герба нашего города?(79 чел знают,44 не знают)
Проценты в торговле:
Мама хотела купить себе пуховик за 2700 руб. в магазине «Эконом». А 4 ноября была распродажа. Скидка на весь товар 20%. За сколько рублей мама купит пуховик на распродаже?
(2160 руб)
т
Скидка 20%
От нашего повара мы узнали,что
% есть и в столовых
При смешивании 5%-ного раствора кислоты с 40% -ным раствором кислоты получили 140г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?
Рассмотрим старинный способ решения этой задачи.
Друг под другом пишутся содержания кислот имеющихся растворов, слева от них и
примерно посередине – содержание кислоты в растворе, который должен получиться
после смешивания. Соединив написанные числа чёрточками получим такую схему:
30
5
40
Рассмотрим пары 30 и 5, 30 и 40. В каждой паре из большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки . Получится такая схема:
10
30
5
40 25
Из неё делается заключение, что 5% раствора следует взять 10 частей,
а 40% 25 частей, .(10+25=35частей всего, 140:35=4г-вес одной
части, 4×10=40г, 4×25=100г.)
т.е. для получения 140г. 30% — ого раствора нужно взять
5% — ого раствора 40г., а 40% — ого — 100г
По телевизору я услышал что курящий человек сокращает свою жизнь на 15%, что составляет 8,4 года. Какова средняя продолжительность жизни в России? (56)
Еще одна задача
Раньше Вася решал правильно две задачи на проценты из двадцати. После изучения темы на одном полезном сайте, Вася стал решать правильно 16 задач из 20. На сколько процентов поумнел Вася? За стопроцентный ум считаем 20 решённых задач(70%)
Задача из ЕГЭ
Тетрадь стоит 40 рублей. Какое наибольшее количество таких тетрадей можно купить на 650 рублей, после понижения цены на 15%? (19)
А вот, что мы узнали от наших родителей:
1. Семейный бюджет (за месяц):
| Наименование | руб | % |
| Мама | 15 000 | 100 |
| Бабушка | 13 000 | |
| Итого | 28 000 | |
| Расходы Остаток | 21770 6230 |
2. Распределение семейного бюджета на ноябрь:
| Коммунальные услуги | 2000 руб | 9% |
| Мобильные телефоны (все) | 600 руб | 2,8% |
| Питание | 6600 руб | 30,3% |
| Одежда, обувь | 4000 руб | 18,4% |
| Кредит | 5000 руб | 23% |
| Транспортные расходы | 520 руб | 2,4% |
| Лекарства | 1000 руб | 4,6% |
| Развлечения (концерт) | 300 руб | 1,4 |
| Сладости | 1500 руб | 6,9% |
| Другое (стрижка) | 250 руб | 1,2% |
| Итого | 21770 | 100% |
Мы выбрали эту тему потому, что нам нравится математика и мы считаем, что математику надо знать хорошо.
Делаем выводы
- Мы выбрали эту тему потому, что нам нравится математика и мы считаем, что математику надо знать хорошо.
- Мы хотели получить полноценные представления о процентах, об их роли в повседневной жизни.
- Мы подумали как это важно, понимать и знать проценты и решили: чтобы быть хорошими специалистами и быть успешными на 100%, необходимо хорошо учиться.
- Крамор В.С. «Повторяем и систематизируем школьный курс алгебры и начало анализа». М., «Просвещение» 1990 год.
- Журнал «Математика в школе.» 1998г.№5.
- Ф.Ф. Нагибин «Математическая шкатулка» М.«Просвещение»1988год.
- https://yandex.ru/images/
- http://infourok.ru/
- https://ru.wikipedia.
МБОУ БГО ООШ№9
Образовательная область: «Математика», «Информатика»
Предмет: «Математика»
Проценты в нашей жизни
Выполнил: Филичкин А.Ю.,
учащийся 6 «А» класса
Руководитель: Шерстяных В.Н., учитель математики,
Борисоглебск
2017
Содержание
Введение…………………………………………………………………..……..……………3
1. Основные сведения о процентах………………………………………………………….4
1.1. История возникновения термина и знака……………………………………………4
1.2. Проценты в нашей жизни……………………………………………………………4
1.3. Интересные факты в процентах………………………………………………………5
2. Применим проценты в жизнь
2.1. Проценты и площади…………………………………………………………………6
2.2. Проценты в нашей школе и классе…………………………………………………..6
Заключение………………………………………………………………………..……..……9
Литература………………………………………………………………………..………….10
Введение
В математике есть термин,
Именуется «процент».
Я вам с точностью отвечу:
Проще ничего и нет.
Это, кто ещё не знает,
Одна сотая числа.
Кто процент легко считает,
Тот повсюду голова.
Измеряются в них скидки,
Что торговцы нам дают,
Вклады в банках и кредиты,
И инфляция валют.
До средних веков человечество прекрасно обходилось без процентов, но с развитием математики, торговля в Европе обрела десятичные дроби, а с ними и проценты. Произошло это лишь в 15 веке.
Цель моей работы: доказать важное значение процентов в жизни человека.
Для достижения цели были поставлены и решены следующие задачи:
-
Изучить историю возникновения процентов;
-
Рассмотреть основные области применения процентов;
-
Познакомиться с интересными фактами о процентах;
-
Научиться рассчитывать процентные соотношения.
1. Основные сведения о процентах
1.1. История возникновения термина и знака
Слово процент от латинского слова «pro centum»,что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов.
Так же проценты были особенно распространены в Древнем Риме. Задолго до существования десятичной системы счисления, вычисления часто производились с помощью дробей, которые были множителями, были кратны 1/100. Например, Октавиан Август взимал налог в размере 1/100 на товары, реализуемые на аукционе.
И в Индии были известны проценты ещё в V в., так как именно в Индии с давних пор счет велся в десятичной системе счисления. Там математики вычисляли проценты, применяя «тройное правило», то есть пользуясь пропорцией.
Знак «%» происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения в скорописи буквы t в наклонную черту произошёл современный символ для обозначения процента. Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошёл в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга — руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.
1.2. Проценты в нашей жизни
В повседневной жизни люди сталкиваются с процентами ежедневно.
При посещении магазинов мы видим яркие объявления о скидках и распродажах. Выгода распродаж для покупателей очевидна – это возможность приобрести качественный товар по сниженным ценам.
В последние годы в средствах массовой информации довольно часто можно услышать о повышении тарифов на коммунальные услуги. Как правило, все цифры озвучиваются в процентах. С 1 июля 2016 года в России тарифы ЖКХ повысились в среднем на 8,3%. Плата за газоснабжение увеличилось на 7,5%, за теплоснабжение – на 8,4%, за электроэнергию – на 8,5%, за горячую и холодную воду, а также за водоотведение – на 9,1%.
Кредиты в банковской сфере выдаются людям под процент. Также очень многие люди в целях безопасности и увеличения суммы денег хранят свои денежные средства в банках под процентами.
На выборах победа партии или кандидата так же определяется в процентах.
Медицинские работники ежедневно сталкиваются с умением рассчитать проценты, например, при инъекциях, для разбавления препарата. Покупая любое лекарство больной перед его использованием внимательно изучает инструкцию к нему, в которой подробно перечислен состав препарата с указанием процентного содержания всех входящих в него веществ.
Бухгалтер любого предприятия ежемесячно рассчитывает прибыль, полученную предприятием, начисляет заработную плату всем сотрудникам предприятия, производит отчисления в налоговую инспекцию, пенсионный фонд, в фонд социального страхования и прочие. Все отчисления рассчитываются индивидуально для каждого сотрудника, но при этом бухгалтер пользуется единой для всех процентной ставкой.
Умение вычислять проценты очень важно при приготовлении сплавов, например, для получения сплава золота 585 пробы необходимо 58.5% чистого золота и два основных лигатурных металла: медь (33.5%) и серебро (8%). Из-за достаточно большого количества золота, внешний вид изделия из 585 пробы не тускнеет в процессе эксплуатации.
1.3. Интересные факты в процентах
Все живые животные и растительные существа состоят из воды: животные – на 75%, рыбы – на 75%, медузы – на 99%, картофель — на 76%, помидоры — на 90%, огурцы — на 95%, яблоки — на 85%, арбузы — на 96%. Даже человек состоит из воды. 86% воды содержится в теле у новорожденного и до 50% у пожилых людей.
Если человек теряет 2% воды от массы своего тела, то у него возникает сильная жажда. Если проценты потерянной воды увеличатся до 10, то у человека начнутся галлюцинации. При потере в 12% человек не сможет восстановиться без помощи врача. При потере в 20% человек умирает.
Вода не только дарит жизнь, но может и отнимать ее, 85% всех заболеваний в мире передается с помощью воды.
Страна с самым большим количеством озёр: Канада. 60% всех озёр мира находятся на территории Канады: более 3 000 000 озёр, занимающих 9% канадских земель.
Самая засушливая страна: Ливия. 99% Ливии покрыто пустыней.
Страна — крупнейший производитель кислорода в мире: Россия. В Сибири растёт примерно 25% мировых лесов, которые охватывают площадь больше, чем континентальная часть США, что делает Россию самым мощным в мире переработчиком углекислого газа в ценнейший кислород.
2. Применим проценты к жизни
2.1. Проценты и площади
Интересно, а сколько составляет в процентах площадь Воронежской области от всей площади Российской Федерации? После расчетов мы узнали, что это всего 0,3%!
Рисунок 2.1 – Соотношение площади Воронежской области к РФ
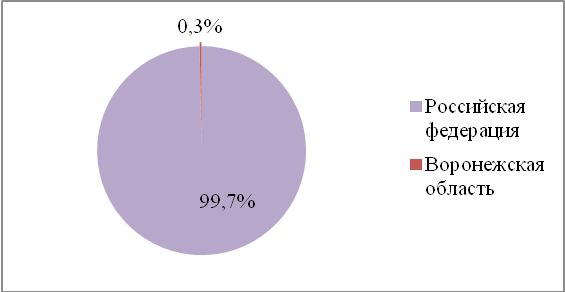
А Борисоглебский район, сколько составляет процентов от Воронежской области? Оказывается, что это 2,63%.
Рисунок 2.2 – Соотношение площади Борисоглебского района к Воронежской области
2.2. Проценты в нашей школе и классе
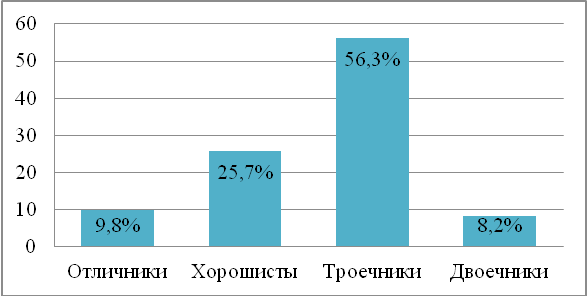
Всю нашу школу можно представить в виде процентов. Итак, всего учащихся 366 человек, из них отличников – 36, хорошистов – 94, троечников 206 и 30 двоечников. Рассмотрим данные показатели в процентом соотношении от общего количества учащихся школы и построим диаграмму.
Рисунок 2.3 – Успеваемость в школе
В нашей школе отличников 9,8%, хорошистов 25,7%, 56,3% троечников и 8,2% двоечников.
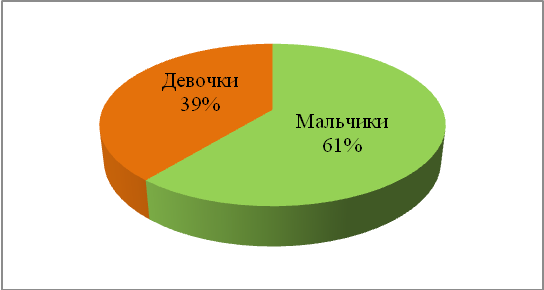
А сколько процентов в нашем классе мальчиков и девочек, если всего в классе 23 ученика? На диаграмме видно, что мальчиков 61%, а девочек 39%.
Рисунок 2.4 – Соотношение мальчиков и девочек в классе
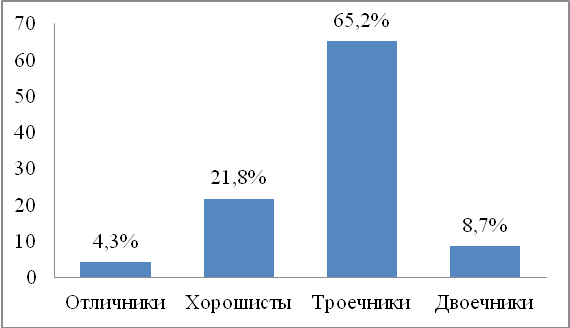
Теперь узнаем, сколько в классе отличников, хорошистов и троечников, а может, есть и двоечники? На диаграмме видно, что итогам второй четверти в классе преобладающий процент троечников – 65,2%, хорошистов 21,8%, 8,7 % двоечников и 4,3% отличников.
Рисунок 2.5 – Успеваемость в классе
На рисунке 2.6 представлена диаграмма цвета глаз нашего класса.
Рисунок 2.6 — Диаграмма цвета глаз
В нашем классе преобладают ребята с зелеными и голубыми по 34,8%, меньше всего ребят с серыми глазами всего 13%.
Интересно узнать какой цвет является самым любимым среди моих одноклассников. Рассмотрим рисунок 2.7.
Рисунок 2.7 – Любимый цвет
Больше всего ребята любят зеленый цвет. То ли в шутку, то ли всерьёз как-то, кто-то изрёк: гении выбирают зелёный цвет. Удивительно, но исследования подтверждают, что в этом изречении заложен глубокий смысл. Может быть, в нашем классе есть будущие гении и у нас их 39%!
Заключение
Итак, роль процентов в жизни человека велика. Они имеют широкое практическое применение в промышленности, медицине, науке и многих других отраслях. С помощью процентов более ярко можно донести нужную информацию до любого человека. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни. Проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты и поэтому очень распространены.
Уметь грамотно и экономно проводить элементарные процентные вычисления должен каждый современный учащийся. В последнее время экзамен по математике проводится в форме ЕГЭ, и в контрольно-измерительных материалах ЕГЭ присутствует задача на проценты. Поэтому нужно как можно лучше знать и уметь пользоваться этой темой.
Список литературы:
-
http://math-prosto.ru/?page=pages/reports/percent-math.php
-
http://rasnajamatematika.blogspot.ru/2013/05/blog-post.html
-
https://infourok.ru/osobennosti-izucheniya-temi-procenti-378938.html
-
http://livescience.ru/Статьи:Говорящие-проценты
-
https://znanija.com/task/550997
-
http://secrets-world.com/interesting/779-20-interesnyh-faktov-o-stranah-mira.html
-
http://pikabu.ru/story/faktyi_o_vode_731461
12