Характеристика класса В классе 6 человек: 4 учатся на «4» и «5» , один на «4» и «3» , один на «3».
Средства, обеспечивающий учебный процесс на уроке: рабочая тетрадь, линейка, карандаш, мультимедийный проектор, презентация к уроку, карточки с заданием.
- Организационный момент.
Цели, которая должна быть достигнута учащимися на данном этапе урока: эмоционально настроиться на успешную работу.
Цель: создать условия для успешного повторения и изучения нового материала, положительного эмоционального настроя на работу. Создание ситуации успеха для каждого учащегося.
Задачи: мобилизировать учеников для активной работы на уроке.
Метод организации работы учащихся: словесный метод.
Деятельность учащихся
Деятельность учителя
Примечание
Включаются во взаимодействие с одноклассниками и с учителем.
В паре улыбаются друг другу.
Дети проверяют готовность рабочего места.
Учащиеся записывают в тетрадях дату проведения урока, вид работы (классная работа), тему урока: («Координатная плоскость»).
Ребята! Я рада вас видеть сегодня на уроке в хорошем настроении.
Посмотрите друг на друга, улыбнитесь, глазками пожелайте товарищу хорошего рабочего настроения.
Я тоже вам желаю сегодня хорошей работы.
Проверьте наличие рабочей тетради, дневника, учебника, ручки, карандашей, инструментов.
Записать в тетрадях дату проведения урока, вид работы (классная работа), тему урока: («Координатная плоскость»).
(Презентация, слад 1).
2. Опрос учащихся по заданному на дом материалу.
Цель, которую учитель ставит перед учениками на данном этапе урока: определить степень усвоения материала и разобраться в своих недочетах.
Цель: проверить выполнение домашнего задания.
Задача: Установить правильность и осознанность выполнения домашнего задания. Устранить обнаруженные пробелы. Активизация и актуализация опорных знаний и умений.
Методы, способствующие решению поставленных целей и задач: объяснительный, репродуктивный, наглядный.
Критерии достижения целей и задач: качественное выполнение домашнего задания.
Методы организации совместной деятельности учащихся: фронтальный, индивидуальный, личностно-адаптированный.
Методы мотивирования учебной активности учащихся в ходе опроса: объяснительный, личностно-адаптированный, сотрудничество.
Методы и критерии оценивания ответов учащихся в ходе опроса: промежуточный контроль, поощрение и благодарность ученикам.
- определение возможных действий педагога в случае, если ему или учащимся не удается достичь поставленных целей;
Деятельность учащихся
Деятельность учителя
Примечание
Проверяют правильность выполнения домашнего задания. Задают вопросы.
1. Прямую, с выбранными на ней началом отсчёта, единичным отрезком и направлением, называют координатной прямой.
2.Работают по карточке с заданием №1. Записывают координаты. Проверяют.
Создание условий для выявления качества усвоения знаний, определение типичных недочетов и выявление причин их появления; ликвидация их недостатков. Рассматриваются решения задач, которые вызвали затруднения при решении дома.
Выполнение учащимися упражнений для повторения:
1.Какая прямая называется координатной прямой? (Презентация, слад 2)
2.Найдите координаты точек A, B, C, D. (Презентация, слад 3-5)
3.Изучение нового учебного материала.
Учебная цель: научиться строить точки на координатной плоскости; определять координаты точек, построенных на координатной плоскости.
Цели: познакомить учащихся с понятием «Координатная плоскость»;
рассказать о Р. Декарте, который ввёл понятие координатная плоскость;
показать на примерах использование понятия координатная плоскость в других областях;
в игровой форме закрепить принцип построения точек на координатной плоскости.
Задачи:
1) ввести понятие координатной плоскости;
2) научить учащихся строить точки на координатной плоскости;
3) научить учащихся определять координаты точек, построенных на координатной плоскости.
4)развитие логического и математического мышления, четкости и аккуратности выполнения.
Основные положения нового учебного материала:
1) Две перпендикулярные координатные прямые-x и y, которые пересекаются в начале отсчета — точке О, называют системой координат на плоскости, а точку О –началом координат.
2)Плоскость, на которой выбрана система координат, называют координатной плоскостью.
3)Пара чисел, определяющая положение точки на плоскости, называется координатами данной точки.
4)Координаты точки на плоскости, соответствующую x называют абсциссой, а соответствующую y – ординатой.
Координатную прямую x называют осью абсцисс, а координатную прямую y называют осью ординат.
5)Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината. И наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Формы и методы изложения нового учебного материала: постановка проблемы урока, её обсуждение, объяснение, метод иллюстраций.
Основные формы и методы организации индивидуальной и групповой деятельности учащихся: словесный. наглядный метод, самостоятельная работа.
Критерии определения уровня внимания и интереса учащихся к излагаемому педагогом учебному материалу: качественное выполнение заданий, вопросы по излагаемому материала, желание выполнять задание.
Методы мотивирования учебной активности учащихся в ходе освоения нового учебного материала: слово учителя, подготовка проблемных вопросов, работа с презентацией, создание ситуации успеха.
Деятельность учащихся
Деятельность учителя
Примечание
Высказывают свое мнение по данной проблеме.
Учащиеся рассуждают.
Слушают рассказ учителя.
Работают в тетрадях.
Учащиеся самостоятельно в тетрадях записывают координаты, отмеченных на координатной плоскости точек.
Проверяют правильность выполнения.
Учащиеся в тетрадях чертят координатную плоскость по заданным размерам.
Работают по карточке с заданием №2
По завершению этой работы учащиеся определяют, что получилось на рисунке.
Как определить положение точки на плоскости?
Где мы в жизни сталкиваемся с координатами?
(Слайд № 6) при посещении кинотеатра
(Слайд № 7) во время любимой всеми игры в «Морской бой»
(Слайд № 
Рассказать учащимся об авторе координатной плоскости Рене Декарте. (Слайд № 9).
Учитель прорисовывает каждое новое понятие с помощью анимации на слайде.
(Слайд № 10). Знакомство с прямоугольной декартовой системой координат введение горизонтальной координатной прямой (оси абсцисс), вертикальной координатной прямой (оси ординат), обозначение точки пересечения осей началом координат.
(Слайд №11). Определение координат точки, отмеченной на координатной плоскости и знакомство с названиями координат точки (абсциссой и ординатой).
(Слайд №12). Учитель предлагает учащимся самостоятельно в тетрадях записать координаты, отмеченных на координатной плоскости точек. Затем на слайде производим проверку самостоятельно выполненной работы.
(Слайд № 13) Творческая работа. Построить фигуру, последовательно соединяя заданные точки на координатной плоскости. На слайде записаны координаты точек, которые надо последовательно отметить на координатной плоскости, и начерчена координатная плоскость.
Затем мы вместе при помощи анимации строим точки на плоскости и последовательно соединяем их отрезками.
Проблемная ситуация.
Начинается совместная работа учителя и учащихся.
Творческая работа.
4.Закрепление учебного материала.
Учебная цель: выяснить, насколько ученики усвоили новый материал (умение строить точку по ее координатам).
Цели и задачи учителя: развитие умения анализировать и оценивать результаты работы.
Формы и методы достижения поставленных целей: учебно-познавательные, учебно-адаптивные, самостоятельная работа.
Критерии, позволяющие определить степень усвоения учащимися нового учебного материала: качественное выполнение заданий в тетради, устные ответы на вопросы, оценка деятельности учащихся на уроке.
Возможные пути и методы реагирования на ситуации: при неусвоении частью учеников нового учебного материала рекомендую использовать работу по образцу, наводящие вопросы учителя при выполнении самостоятельной работы.
Деятельность учащихся
Деятельность учителя
Примечание
Выполняю самостоятельную работу по вариантам.
Проверка задания по вариантам.
Учащиеся отвечают на вопросы
(Слайд № 14). Учащимся предлагается самостоятельно по вариантам выполнить подобную творческую работу. Раздаются карточки с заданием №3.
(Слайд № 15) Проверка задания варианта № 1.
(Слайд № 16) Проверка задания варианта № 2.
Подведение итогов по вопросам:
1.Как называются оси координат?
2.Как называют пару чисел, определяющих положение точки на плоскости?
3. Как называют первое число? Как называют второе число?
4.Какой необходимо соблюдать порядок при записи координат точек?
Самостоятельная работа учащихся по закреплению изученного на уроке материала.
5. Задание на дом.
Цель самостоятельной работы учащихся: в ходе выполнения домашнего задания ученики должны выучить основные понятия п. 45, выполнить творческое задание по выбору (№1, №2)
Цель учителя: умение выделять главные мысли, обосновывать свое мнение, уметь делать выводы, знать изученный материал, делать сравнительный анализ.
Критерии успешного выполнения домашнего задания: правильность выполнения домашнего задания, аккуратность, свободное владение материалом в процессе фронтального опроса.
Деятельность учащихся
Деятельность учителя
Примечание
п.45 (приложение с творческим заданием).
1.Выполнить практическую работу по предложенной учителем карточке (построить фигуру, последовательно соединяя точки на координатной плоскости)
2.Самому придумать творческую работу.
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.
Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».
После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
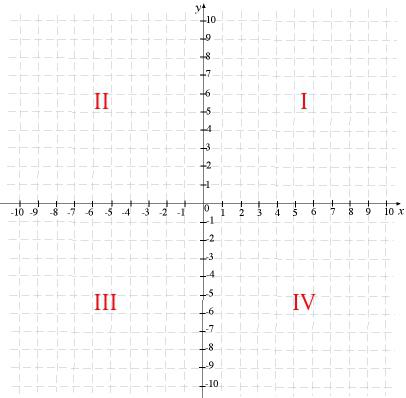
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
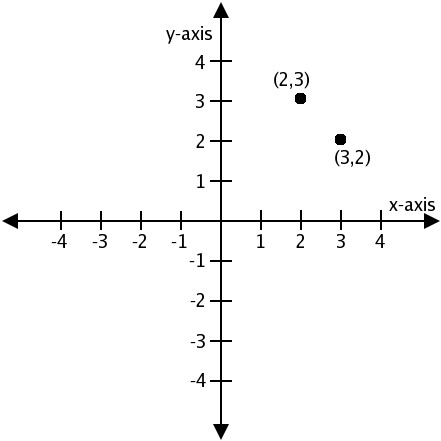
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
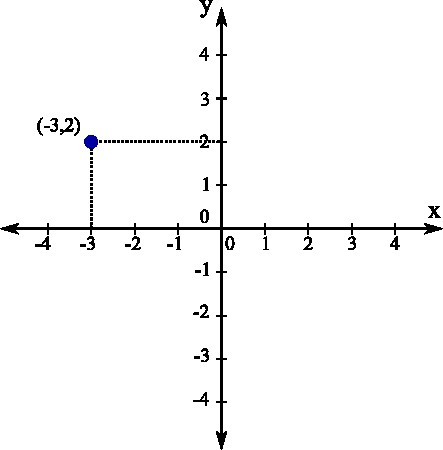
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.
Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
§ 7. Координатная плоскость
1. Оси координат и отыскание координат точки на плоскости
На координатной прямой «прописаны» точки-жильцы, у каждой точки есть свой номер дома — её координата. Если же точка берётся в плоскости, то для её «прописки» нужно указывать не только номер дома, но и номер квартиры. Напомним, как это делается.
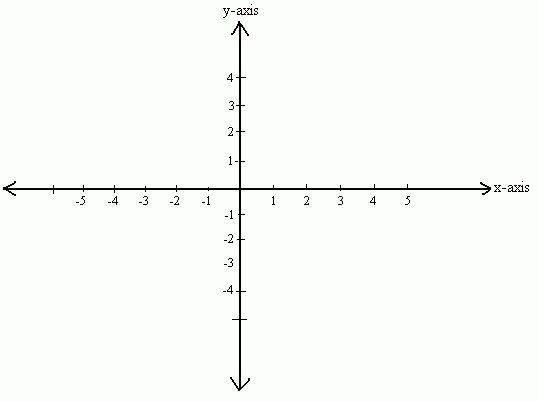
Проведём две взаимно перпендикулярные координатные прямые и будем считать началом отсчёта на обеих прямых точку их пересечения — точку О. Тем самым на плоскости задана прямоугольная система координат (рис. 17), которая превращает обычную плоскость в координатную. Точку О называют началом координат, координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами. Координатные углы нумеруют так, как показано на рисунке 17.
А теперь обратимся к рисунку 18, где изображена прямоугольная система координат и отмечена точка М. Проведём через точку М прямую, параллельную оси у. Прямая пересекает ось х в некоторой точке, у этой точки есть координата на оси х (для точки, изображённой на рис. 18, эта координата равна -1,5), её называют абсциссой точки М. Далее проведём через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата на оси у (для точки М, изображённой на рис. 18, эта координата равна 2), её называют ординатой точки М. Коротко пишут так: М(х; у) (для точки на рисунке 18 имеем М(-1,5; 2)). Абсциссу записывают на первом месте, ординату — на втором. Используют, если в этом есть необходимость, и другую форму записи: х = -1,5; у = 2.
На практике для отыскания координат точки М обычно вместо прямых, параллельных осям координат и проходящих через точку М, строят отрезки этих прямых от точки М до осей координат (рис. 19).
Замечание. В предыдущем параграфе мы ввели разные обозначения для числовых промежутков. В частности, как мы условились, запись (3; 5) означает, что на координатной прямой рассматривается интервал с концами в точках 3 и 5. В настоящем же параграфе пару чисел мы рассматриваем как координаты точки; например, (3; 5) — это точка на координатной плоскости с абсциссой 3 и ординатой 5. Как же правильно по символической записи определить, о чём идёт речь: об интервале или о координатах точки? Обычно это бывает ясно из контекста.
Учитывая введённые термины и обозначения, горизонтальную координатную прямую называют осью абсцисс или осью х, а вертикальную координату …
Именно так мы и действовали, находя координаты точки М на рисунке 18.
Если точка Mi(x; у) принадлежит первому координатному углу, то х > 0, у > 0; если точка Мг(л:; у) принадлежит второму координатному углу, то х < 0, у > 0; если точка М3(х; у) принадлежит третьему координатному углу, то х < 0, у < 0; если точка Mi(x; у) принадлежит четвёртому координатному углу, то х > 0, у < 0 (рис. 21).
А что будет, если точка, координаты которой надо найти, лежит на одной из осей координат? Пусть точка А лежит на оси х, а точка В — на оси у (рис. 22). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, её координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси х: сама ось х пересекает ось у в точке О с координатой (ординатой) 0.
В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; -1,5). А для точки О имеем 0(0; 0).
Вообще любая точка на оси х имеет координаты (х; 0), а любая точка на оси у — координаты (0; у).
2. Построение точки на плоскости по её координатам
Выше мы обсудили, как находить координаты точки на координатной плоскости. А как решать обратную задачу, т. е. как, задав координаты, построить соответствующую точку? Чтобы выработать алгоритм, проведём два вспомогательных, но в то же время важных рассуждения.
Первое рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси у и пересекающая ось х в точке с координатой (абсциссой) 4 (рис. 23). Любая точка, лежащая на этой прямой, имеет абсциссу 4. Так, для точек Мь М2, М3 имеем Мх(4; 3), М2(4; 6), М3(4; -2). Иными словами, абсцисса любой точки М прямой I удовлетворяет условию х = 4. Если же взять точку, не лежащую на этой прямой, то её абсцисса будет отлична от 4. Говорят, что х = 4 — уравнение прямой I или что прямая I (и только она) удовлетворяет уравнению х = 4.
На рисунке 24 изображены прямые, удовлетворяющие уравнениям х — -4 (прямая 1), х = — 1 (прямая Z2), х = 3,5 (прямая 13). А какая прямая удовлетворяет уравнению х = 0? Догадались? Ось у.
Второе рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси х и пересекающая ось у в точке с координатой (ординатой) 3 (рис. 25). Любая точка, лежащая на этой прямой, имеет ординату 3. Так, для точек Мь М2, М3 имеем: МД0; 3), М2(4; 3), М3(-2; 3). Иными словами, ордината любой точки М прямой I удовлетворяет условию у = 3. Если же взять точку, не лежащую на этой прямой, то её ордината будет отлична от 3. Говорят, что у = 3 — уравнение прямой I или что прямая I (и только она) удовлетворяет уравнению у — 3.
На рисунке 26 изображены прямые, удовлетворяющие уравнениям у = -4 (прямая 1{), у = -1 (прямая Z2)> г/ = 3,5 (прямая 13). А какая прямая удовлетворяет уравнению у = 0? Догадались? Ось х.
Заметим, что математики, стремясь к краткости речи, говорят «прямая х = 4», а не «прямая, удовлетворяющая уравнению х = 4». Аналогично они говорят «прямая у = 3», а не «прямая, удовлетворяющая уравнению у = 3». Мы будем поступать точно так же.
Подведём итоги.
Чтобы построить на координатной плоскости хОу прямую х — а, нужно:
- 1) отметить на оси х точку с абсциссой а;
- 2) провести через неё прямую, параллельную оси у.
Чтобы построить на координатной плоскости хОу прямую у = b, нужно:
- 1) отметить на оси у точку с ординатой b;
- 2) провести через неё прямую, параллельную оси х.
Вернёмся теперь к рисунку 18. Обратите внимание, что точка М(-1,5; 2), которая там изображена, есть точка пересечения прямой х = -1,5 и прямой у = 2. Теперь, видимо, будет понятен алгоритм построения точки по заданным её координатам.
Алгоритм построения точки М(а; b) в прямоугольной системе координат хОу
- Построить прямую х = а.
- Построить прямую у = b.
- Найти точку пересечения построенных прямых — это и будет точка М(а; b).
ПРИМЕР 1. В системе координат хОу построить точки: А(1; 3), В(-2; 1), С(4; 0), D(0; -3).
Решение: Точка А есть точка пересечения прямых х = 1 и у = 3 (рис. 27). Точка В есть точка пересечения прямых х — -2 и у = 1. Точка С принадлежит оси х, а точка D — оси у.
Рене Декарт (1596—1650), французский философ, математик, физик, физиолог.
Впервые прямоугольную систему координат на плоскости стал активно использовать Рене Декарт для решения геометрических задач алгебраическими методами и, обратно, для замены алгебраических моделей геометрическими. Поэтому иногда говорят: «декартова система координат», «декартовы координаты».
ПРИМЕР 2. В координатной плоскости хОу дана точка М(3; 2). Построить точку, симметричную точке М: а) относительно оси х; б) относительно оси у, в) относительно начала координат. Указать координаты построенных точек.
Решение: а) Точка М(3; 2) указана на рисунке 28 — это точка пересечения прямых х = 3, у = 2. Точка Р симметрична точке М относительно оси х, её координаты таковы: Р(3; -2). Обратите внимание: абсцисса осталась прежней, а знак ординаты изменился.
б) Точка N симметрична точке М относительно оси у, её координаты таковы: N(~3; 2). Обратите внимание: ордината осталась прежней, а знак абсциссы изменился.
в) Точка К симметрична точке М относительно начала координат, её координаты таковы: К(-3; -2). Обратите внимание: изменились знаки обеих координат.
Вопросы для самопроверки
- Что такое прямоугольная система координат на плоскости?
- Сформулируйте алгоритм отыскания координат точки М, заданной в системе координат хОу.
- В какой четверти координатной плоскости хОу находится точка М(х; у), если: а) х < 0, у > 0; б) х > 0, у < 0; в) х < 0, у < 0; г) х > 0, у > 0?
- Как на координатной плоскости хОу построить прямую: а) х = а; б) у = b?
- Какая прямая в координатной плоскости хОу задаётся уравнением: а) х = 0; б) у = 0?
- Сформулируйте алгоритм построения точки М(а; b) в прямоугольной системе координат хОу.
- Как на координатной плоскости расположены друг относительно друга точки: М{а; b) и Р(а; -b); М(а; b) и N(-a; b); М(а; b) и К(-а; -b)?