В детском возрасте ребенок усваивает информацию лучше всего. Поэтому родители стараются дать как можно больше знаний своему чаду. Математические сказки про геометрические фигуры — это отличный способ познакомить ребенка со сложным предметом. Не всем взрослым понятны школьные задачки, а ребенку и подавно не объяснишь, что такое равнобедренный треугольник и почему овал не круглый. Именно для того чтобы математика стала понятной и доступной, были придуманы сказки для 1 класса, которые так нравятся детям.
Геометрия
В чудной стране, где почему-то обитают точки, линии и различные фигуры, каждый день происходят странные и смешные истории. Геометрия — наука очень сложная, но если добавить волшебства с помощью воображения, то окажется, что во всех этих треугольниках, параллелепипедах и даже овалах нет ничего страшного.
Математические сказки про геометрические фигуры появились очень давно. И у каждого учителя имеются свои рассказы. Создано все это было для того, чтобы ребенок не перегружал свой еще не окрепший мозг сложными терминами, при этом легко понимал все темы.
Кстати, математика — это не единственная наука, к которой применимы сказки. Например, всем известный короткий сказ о том, что Иван родил девчонку, велел тащить пеленку, отлично помогает запомнить падежи.
Классификация
При подборе сказочных историй воспитатель должен учитывать возрастные и индивидуальные особенности дошкольников.
Например, есть существенные отличия в сказочных математических историях, предлагаемых дошкольникам и школьникам. Отличия состоят в функции персонажа. Если у малышей Баба-Яга или Колобок занимаются изучением основ геометрии вместе с детьми, то в истории для школьников они выполняют только вспомогательную функцию.
Разные виды геометрических фигур — сюжет для кукольного представления, причем «озвучиванием» сказочных персонажей могут заняться дети.
Сказки могут быть краткосрочными, помогающими отрабатывать конкретные вычислительные действия.
Сказки про фигуры
Несмотря на то, что сама геометрия как предмет появляется только в старшей школе, фигуры и некоторые их свойства изучать начинают в первых классах. Математические сказки про геометрические фигуры бывают очень короткие, буквально из одного предложения. Они могут стать ярким акцентом на занятии. Такие сказки для 1 класса придумывают для того, чтобы дети могли легко запомнить какую-либо информацию. К тому же, они помогают сделать процесс обучения более приятным для детей.
Но все же намного интереснее ребятам слушать продолжительные математические сказки про геометрические фигуры. И одним из самых популярных является рассказ про полезный прямоугольник.
История повествует о геометрических фигурах и о том, что все они очень нужны.
Картотека полезной литературы
- «Путешествие в Цифроград: математическая сказка» Шорыгина Татьяна Андреевна (3 книги).
- «Математические сказки. Пособие для детей 6–7 лет» Ерофеева Тамара Ивановна.
- «Математические сказки. Пособие для детей 5 — 6 лет. В 2 выпусках» Ерофеева Тамара Ивановна, Стожарова Марина Юрьевна.
- «Приключения Треугоши: Математическая сказка для детей от 2-х до 4-х лет» Шевелев Константин Валерьевич.
- «О короле Кролике и хитром Лисе: Математическая сказка для дошкольников 5–7 лет» Лукьянова Антонина Владимировна (худ. Душин М.В.).
- «Приключения Кубарика и Томатика, или Веселая математика» Сапгир Генрих Вениаминович, Луговская Юлия Павловна.
- «Приключения в стране Геометрии» Ерофеева Тамара Ивановна.
- «Математика для малышей в сказках, стихах и загадках. Для детей 3–6 лет» Дерягина Людмила Борисовна.
- «Учимся считать. Веселое путешествие, или Как найти новых друзей и научиться считать до десяти» Горбушин Олег Юрьевич.
- «Цифры, счет и карандашик Коля» Рик Татьяна Геннадиевна.
Сказка «Как подружились Квадрат и Прямоугольник»
В одной геометрической стране жили разные фигуры, в том числе и наши герои. Прямоугольник всю свою жизнь восхищался Квадратом, а как выглядит он сам, ему ну никак не нравилось. Вот ляжет он на животик и сразу становится толстый и низкий, а если во весь рост встанет, то и подавно некрасивый. Жираф какой-то узкий. А Квадрат, слыша все это, восхищался собой, и правда, ну идеален же! Все стороны равны, не то что какой-то там Прямоугольник.
Но вот однажды заблудился один Человек в лесу и повстречал Квадрат и Прямоугольник. Последний сидел грустный-грустный, поэтому Человек попросил помощи у Квадрата. А хотел он всего лишь выяснить, где же его дом. Взобрался Человек на Квадрат, да так ничего не увидел. Как ни крутил он его все одно — только деревья видно и все.
Решил тогда Человек хотя бы через речку переправиться, но и в этом Квадрат не смог помочь, плюхнулся только в воду и промок. Прямоугольник все это видел и решил помочь Человеку. Выпрямился во весь свой рост и стал выше деревьев, тут-то Человек и увидел, куда ему теперь идти. И через речку Прямоугольник лег мостом и помог пройти герою. Квадрат увидел все это и покраснел, понял он, что не каждое совершенство является таким. С тех пор и дружат две фигуры.
Вот так сказка «Как подружились Квадрат и Прямоугольник» показала, что недостаток может быть и преимуществом.
Рассказы про геометрические фигуры
Конечно, сказки бывают разными и в каждом городе, в каждой школе их рассказывают по-разному. Но все же смысл не меняется, в каждой истории есть свой урок и разъяснение по поводу того, как выглядят фигуры и какие свойства они имеют. Вот, например, математическая сказка «Квадрат и Треугольник» повествует о том, что не всегда можно поодиночке справиться. Все же две головы иногда лучше, чем одна.
Но помимо этого, в рассказе описан тот факт, что фигуры бывают разными. Треугольник может быть и прямоугольным, и равнобедренным, и так далее. Все это — важные знания, которые в будущем точно пригодятся ребенку.
Лесная история
В некотором царстве, математическом государстве, жила-была семья зайчиков. Все они были похожи друг на друга, но имена у них были разные. Разные и необычные. Папу звали «Один», он был самый высокий, маму – «Два», она была чуть пониже папы, а их деток звали: «Три», «Четыре» и «Пять». Три был самым старшим, и он во всём старался помогать своим родителям. Четыре – был средним: пониже Три и повыше Пять, он часто присматривал за своим младшим братом. А Пять был совсем маленьким и ничего не умел делать. Семья Зайчиков жила в маленьком домике, на Лесной опушке, в тени трёх высоких дубов, рядом протекал ручей, над которым склонялись две ивы. Зайчата быстро подрастали и в их маленьком домике уже не хватало места для всей семьи. Решили Зайцы построить себе новый большой дом, чтобы в нём было два этажа: один этаж для больших Зайчиков, и один – для маленьких. Строить решили из берёзовых веток, да и путь к берёзовой роще был коротким: пройдёшь по узкому мостику через ручеёк, повернёшь влево – и ты на месте! Вся заячья семья пришла в рощу. Папа набрал самую большую охапку из десяти толстых веток, мама – Зайчиха – чуть поменьше – девять веток, её ветки были тоньше, но тоже прочными. Старший сын набрал веток больше всех своих братьев, средний больше чем младший, а младший маленько, но зато веточки были тонкие и гибкие. Стали зайцы возвращаться на опушку по той же короткой дороге, да по узкому мостику, да вот беда! С широкими охапками никак не пройти по узкому мостику! Загрустили зайчики. Высоко на дереве сидела Ворона. Она сказала: «Не грустите зайчата, здесь есть другая дорога, она немного длиннее, но пошире и вам будет удобнее по ней пройти». А ещё она позвала на помощь зайчатам пять крепких медвежат. Все они вместе легко добрались до опушки. Потом весело и дружно построили новый большой дом. На новоселье к ним пришли гости: десять белок, шесть лисят и пять дружных медвежат.
Сказка о трёх царевнах
В далёком царстве жил царь с тремя дочками. Они любили по вечерам решать задачки и разгадывать загадки. За каждый правильный ответ царевны получали по подарку. Старшая царевна любила получать подарки из золота, средняя царевна из бриллиантов, а младшая любила цветы и животных. Однажды вечером царь сказал: «Я привёз из дальних стран много разных подарков. Кто из моих дочек правильно решит задачки – тот и получит подарки. Задача №! – Для старшей царевны: сорви с одной яблони 5 жёлтых яблок, а с другой 5 красных яблок. Сколько всего яблок ты сорвала? Задача №2 – Для средней царевны: в твоей шкатулке лежат 6 колец с бриллиантами. Я тебе привёз ещё 2 кольца. Сколько всего у тебя будет колец? Задача № 3 – Для младшей царевны: у тебя было 9 котят, а 2 убежали. Сколько осталось котят?» Все царевны решили свои задачи правильно, и царь подарил старшей царевне золотой сундучок, средней царевне 2 кольца с бриллиантами, а младшей царевне весёлого щенка. Вот тебе сказка, а мне кринка масла.
Про 0 и 1
Жили- были в городе Математики числа и цифры. Они всегда спорили кто важнее и старше, даже придумали для себя необычные знаки «<�», «>», «+», «=», «-». Среди них жили единичка и нолик. Они очень хотели учиться в школе, но их не брали, так как они были маленькие. Думали друзья, думали и придумали, что им надо держаться вместе.
И получилась из них цифра 10. Стали они числом побольше, и их взяли в школу. В городе их стали все уважать. Вот так и стали жить вместе цифры 1 и 0, или число 10. А другие числа посмотрели на их дружбу и тоже стали жить дружнее. Так появились цифры больше 10.
Сказка о двух оценках
В некотором царстве, в далёком государстве, в стране Школьных уроков жили — были не тужили рядом по — соседству две цифры: двойка и пятёрка. Дружба их никак не брала, вечный спор между ними стоял: кто из них главнее? Пятёрка говорила, что она главнее и умнее двойки, что только за хорошие знания можно её получить, а для оценки два знания не нужны. Двойка ей в ответ, что без неё тоже нельзя, тогда не будет стремления для совершенства в учёбе. Что она даёт толчок на дальнейшее стремление к знаниям. Спору их не было конца. А вы, за какую оценку? Вот будете жить поживать, ума наживать, а лиха избегать. Тогда возможно спор их и решится.
Новогодняя сказка
В одну предновогоднюю пору, случилась эта история в нашей семье. Все стали готовиться к празднику. Папа, мама, бабушка, дедушка, сестра Вероника и я, Семён. Семья наша большая, а вы успели нас сосчитать? Папа принёс большую, пушистую, зелёную ёлку. А на ней мы заметили необычный конверт. Что бы это значило, подумали мы все. Открыв конверт, мы поняли, что это послание из далёкой Лапландии, где живёт Дед Мороз. Это письмо было с заданиями. Дед Мороз просил украсить ёлку так, чтобы бабушка повесила на ёлку три шишки, дедушка – пять шаров, мама нарядила ёлку двумя хлопушками, а Вероника повесила четыре конфеты, а я повесил одну гирлянду. А вы успели сосчитать, сколько всего игрушек надо было развесить на ёлке. А на макушку мы водрузили пятиконечную звезду. Кто знает, сколько концов у звезды? А когда наступил Новый год, и мы проснулись. Мы увидели под ёлкой подарки от Деда Мороза, значит, мы правильно выполнили его просьбу.
Дедушке достались часы, бабушке – шаль, маме – духи, папе – удочка, Веронике – кукла, а мне, Семёну – ролики. А вы успели посчитать, сколько подарков принёс нам Дед Мороз?
Про Золушку
В одном сказочном королевстве жила-была девочка по имени Золушка. Была она сирота, воспитывала её мачеха, и были у неё две дочери. Дочери были очень ленивы, и всю работу по дому приходилось делать Золушке. Вот в один прекрасный день Король пригласил всех на бал. Но Золушке мачеха не разрешила ехать на бал. Она приказала Золушке к её возращению решить все задачки, возращению решить все задачки, которые не решили её дочери: • В комнате 4 угла. В каждом углу сидела кошка. Напротив, каждой кошки – 3 кошки. Сколько кошек в комнате? • Как в решете воды принести? • Из какой посуды нельзя ничего съесть? Так же Золушка должна была вымыть посуду: 5 ложек и 5 чашек и 5 тарелок. Сколько получилось вымытой посуды? Когда вернулась мачеха с дочерями домой. Золушка быстро справилась с заданием мачехи и села за рукоделие.
ПРИНЦ КРУГ И КОЛДУН МИНУС
В далёкой стране Математика жили-были король Треугольник и королева Трапеция. И всё у них было хорошо, кроме того, что не было у них детей. Тогда королева решила сходить к злому колдуну Минусу, чтобы он помог ей. Колдун Минус дал королеве зёрнышко и сказал: — Посади его в горшочек и поливай каждое утро, но за это ты должна отдать мне голос своего ребёнка. Королева была так рада, что у неё наконец-то появится ребёнок, и дала согласие колдуну. Когда королева Трапеция вернулась во дворец, сразу же посадила зёрнышко в горшок с землёй и полила его. Шло время зёрнышко росло и превратилось в прекрасный цветок, когда цветок распустился, там оказался прекрасный малыш. Король Треугольник и королева Трапеция были очень рады, они решили назвать маленького принца Круг. Принц рос, но не говорил, и тогда королева вспомнила, что она отдала голос принца злому колдуну Минусу. Она рассказала всё королю Треугольнику, и они решили пойти вместе к колдуну, и попросить его смиловаться и вернуть голос принцу Кругу. Когда король и королева пришли к злому колдуну Минусу, они услышали прекрасный голос. Это был голос колдуна, точнее принца Круга. Тогда они упали перед колдуном Минусом на колени и стали его умолять, чтобы он отдал принцу Кругу голос. Колдун смиловался над ними и сказал: — Я верну голос принцу Кругу, но за это вы больше не будите называть меня злым колдуном. — Мы согласны – сказали король и королева. Король Треугольник выступил перед своими подданными, сказал: — Отныне колдун Минус добрый колдун, а не злой. У принца Круга в эту же минуту появился голос. И все в стране Математика стали жить счастливо.
ПО ГРИБЫ
Однажды Маша отправилась в лес за грибами и заблудилась. Вдруг увидела, катится по дороге Колобок. Говорит Маша Колобку: -Колобок, Колобок, где тут грибы растут? А он ей отвечает: — Не знаю, я спешу, некогда мне, лису ищу, разыскиваю, хочу её съесть. Спроси лучше у цифры Два, «колючей», она всё про грибы знает. Пошла Маша к цифре Два и спросила: — Эй цифра Два, где тут у вас грибы растут? -Там возле домика.
Отвечает цифра Два. Увидела Маша грибы лисички и скорее и их собирать стала. Вдруг из домика Мишка – медведь как выскочит и зарычал на Машу. Испугалась Машенька и скорей побежала подальше от медведя. Прибежала на полянку видит пенёк стоит. Села Маша на пенёк и стала плакать. А мимо летела птица Три. Услышала она, что девочка плачет, подлетела к ней и спрашивает: — Ты чего здесь плачешь на весь лес? — Я потерялась! — говорит Маша. — Не плачь, я тебе помогу, покажу дорогу домой. — Ура, ура! – закричала радостная Маша. — Только пообещай, что никогда больше одна в лес не пойдёшь без взрослых. — Конечно, обещаю – ответила Маша, и они отправились домой.
ДВОЙКИ – ЛЕБЕДИ
В одном волшебном царстве, цифровом государстве, жили-были царь Десятка и царица Девятка. Были они богатые и знатные, но в то же время добрые и весёлые. И было у них двое детей, сын Семёрка и дочь Пятёрка. Дочка была самая красивая и умная, все завидовали царю и ласково называли её Пятёрочка. Захотела Баба Яга украсть Пятёрочку, чтобы получить за неё выкуп у царя. Позвала она своего верного слугу Шестёрку и дала ему наказ украсть Пятёрочку. Шестёрка выслушал Баба Ягу, пошёл в сарай, где у них жили Двойки-лебеди, запряг их в сани и полетел воровать Пятёрочку. А в это время Пятёрочка гуляла в своём любимом цветочном саду, рассматривала невиданной красоты розы и пела песенки. Внезапно всё небо затянуло чёрными тучами, подлетел к ней Шестёрка на своих Двойках-лебедях, схватил её за руки, усадил в сани и полетел обратно к Бабе Яге. Закричала Пятёрочка, что есть мочи: «Батюшка, матушка – помогите!!! Спасите, увозит меня Шестёрка в густой дремучий чёрный лес к Бабе Яге!» Услышали её крик слуги царя и побежали ему сообщить о случившемся горе. Чернее тучи стал царь от горя, узнав о случившемся несчастье, слегла царица. Тут заходит в царские покои к царю сын Семёрка и говорит: «Не печалься Царь-батюшка! Я пойду и спасу сестрицу! Соберу я своё войско из единичек, и пойдём войной на Бабу Ягу!» Отвечает царь: «Нет, сынок Баба Яга не глупа, здесь хитрость нужна! Пойди, сходи к магу Восьмёрке и посоветуйся с ним как лучше сделать?» Пошел, Семёрка к магу, рассказал о беде. И посоветовал Восьмёрка взять палочку-уменьшалочку и шапку-невидимку. Объяснил, как пользоваться этими вещами, если ударишь ты по верному слуге Бабы Яги Шестёрке шесть раз, то он уменьшится до таких размеров, что исчезнет, а если ударишь по Двойке-лебедю два раза, то он уменьшится тоже до таких размеров, что исчезнет. Этим самым ты обезоружишь Бабу Ягу, лишив её верного слуги и Двоек-лебедей. Поблагодарив Мага Восьмёрку Семёрка, взял у него палочку-уменьшалочку, шапку-невидимку и пошёл выручать сестрицу Пятёрочку. Долго он шёл по полям по лесам, наконец, дошёл до дремучего леса Бабы Яги. Надел шапку-невидимку, подкрался к дому Бабы Яги и увидел слугу Шестёрку. Ударил раз по нему палочкой-уменьшалочкой, уменьшился, Шестёрка в размерах и закричал: «Ой-ой-ой! Что такое? Кто здесь?» Ударил Семёрка ещё пять раз и исчез Шестёрка, как будто его и не было. Пошел, Семёрка в сарай и начал хлестать по Двойкам-лебедям палочкой-уменьшалочкой пока они все не исчезли. После этого зашёл он в дом Бабы Яги, не снимая, шапки-невидимки и увидел свою сестрицу Пятёрочку. Она сидела на лавочке и горько плакала. Подошёл к ней Семёрка и зашептал в самое ухо: «Здравствуй сестрица! Не плачь, я тебя сейчас выручу!» Снял он быстро шапку-невидимку с себя и одел её на себя и сестрицу, вышли они из дома Бабы Яги и побежали что есть мочи домой к батюшке и матушке. Очень обрадовался царь Десятка, когда снова увидел свою ненаглядную красавицу дочь Пятёрочку. Царица Девятка выздоровела, и снова они зажили весело и счастливо, как раньше.
В ДЕСЯТОМ КОРОЛЕВСТВЕ
В далеком месте, в Десятом королевстве жил-был добрый пухлый король Ноль. А женат он был на красавице Единице – гордой и вредной девице. И было у короля и королевы две дочери. Старшую звали Двойкой. Она была похожа на мать – такая же стройная, величавая и такая же вредная и заносчивая. Младшая дочь Пятерка – вся в отца – веселушка, хохотушка, в общем – миленькая душка! Как-то раз пошли принцессы погулять к реке у леса. Там купались ребятишки. Пять девчонок, семь мальчишек. Сколько было там детишек? — Эй, принцессы, вы куда? Подходите к нам сюда! Будем вместе веселиться, шутить, прыгать и играть, плавать, бегать, загорать! Пятерка сразу согласилась. К ребятам кубарем скатилась. Ну, а Двойка рассердилась: — Я принцесса! Как посмели меня звать! Негоже с вами мне играть! Эта вся моя река! Буду плавать здесь одна! Убирайтесь кто куда! Стало грустно детворе, и сказали Двойке все: — Ты не лебедь, ты – вреднюка! — Злюка! — Злюка! — И дюдюка! Тут уж Двойка разозлилась… Аж в лице переменилась…Головой она качнула – и детей как ветром сдуло. Мы забыли рассказать, что могла ведь колдовать наша вредная принцесса.
С той поры все дети королевства на уроках стали получать самые худшие школьные оценки – двойки. Нет ничего страшного, если двойка встречается одна или с другими цифрами где-нибудь в книге, на афише или, скажем, на бирке в магазине. Но если двойка появляется в твоем дневнике – это настоящая школьная беда! Кому нужна плохая отметка?! А у мальчишек и девчонок Десятого королевства в дневнике и тетрадях были теперь только такие отметки. Да и в соседних королевствах дети все чаще и чаще приносили домой дневники с двойками. Словно вирус, болезнь распространялось вредное колдовство вокруг. И как бы учителя не старались, как бы родители не строжились – дети все равно учились плохо. Стало жаль Пятерке ребят. Кто же из них теперь вырастет – двоечники, которые ничего не знают и не умеют в жизни? Решила она им помочь – открыть секрет избавления от заклятья. Она услышала его ночью, когда ее старшая сестра бормотала во сне. Но Двойка догадалась о том, что ее сестра хочет рассказать этим вредным детям тайну избавления от плохих оценок. Рассердилась она и на сестру. Наколдовала высокую башню – в 22 метра, далеко-далеко от своего королевства, и упрятала там свою младшую сестру Пятерку. Мол, пусть посидит немного, а то чего удумала, старшей сестре перечить. Все свои волшебные силы потратила Двойка на это колдовство. И так ослабела, что позабыла и о своем вредном волшебстве, и, вот беда, и о секрете исцеления детей, и о своей сестре тоже позабыла. Не на шутку встревожились и опечалились король и королева, узнав об исчезновении своей младшей дочери. Во все четыре стороны света разослал король Ноль своих гонцов с королевским указом. Тому, кто найдет и вернет принцессу Пятерку домой, обещал Ноль свою младшенькую дочь в жены отдать, когда принцесса подрастет, и полкоролевства подарить! Многие пытались найти пропавшую принцессу – все напрасно! И вот как-то раз услышал о принцессе Пятерке храбрый принц далекого королевства Четверка. Он был очень настойчивый, упрямый и трудолюбивый. Решил Четверка во чтобы то ни стало отыскать Пятерку. Долго бродил он по свету, много трудностей и испытаний пришлось пережить отважному принцу. Но он не сдавался! И вот в один прекрасный день увидел он высокую башню. Попытался он проникнуть в нее, но на пути у него возникло новое препятствие. Принцесса Двойка заколдовала башню так, что она никого не впускала, пока путник не отгадает ее загадку. «Мышка яблоко несла и еще одно нашла, — забубнила башня, — громко ухнула сова: «У тебя теперь их…». Сколько яблок у мышки?». Принц с легкостью дал правильный ответ. Башня впустила его. Но на втором этаже ему снова пришлось считать. — Три зайчонка на качелях с аппетитом сушки ели. Два пришли к ним поболтать. Сколько заек? — спросила башня. — Ровно …, — ответил принц. И опять правильно. Так этаж за этажом, загадка за загадкой – добрался Четверка и до последнего. — Девять гусениц ползли, семь из них домой пошли. В мягкой шелковой траве их осталось только…? — Две!!! И, о чудо! Дверь в комнату распахнулась, и принц увидел прекрасную юную принцессу. Это была Пятерка! Принц влюбился в нее без памяти. Вернул он дочь родителям. Как же счастливы были король и королева увидеть родную Пятерочку!!! Королева Единица перестала вредничать после исчезновения младшей дочери, и теперь была такая же добрая, как и ее муж Ноль. Двойка ничего не помнила о своем поступке и тоже от души радовалась возвращению младшей сестренки. Сыграли пышную свадьбу – Четверка и Пятерка стали мужем и женой, а от обещанной половины королевства принц отказался. Не ради него юноша искал принцессу! Да к тому же у него и свое — целое королевство имелось! — А как же дети-двоечники? – спросите вы. Все в порядке! Не волнуйтесь. Они стали отличниками! Секрет в том, что не надо лениться, нужно трудиться, как бы тяжело иногда не было. Домашние задания необходимо выполнять прилежно и вовремя. На уроках не отвлекаться, а внимательно слушать учителя. Уважать родителей и прислушиваться к их советам. Нужно побольше читать полезных и интересных книг о природе, животных, нашей планете. Не забывать и про сказки! И, конечно же, делать зарядку по утрам, вовремя ложиться спать по вечерам, гулять на свежем воздухе, заниматься спортом, чтобы хорошо работала не только наша голова, но и тело. Чтобы мы всегда чувствовали себя хорошо и многого смогли достичь в жизни! Выполняя все эти нехитрые правила, ребята Десятого королевства и соседних земель быстро исправили все двойки на пятерки – пятерок они получили столько, что двойки сами улетучились из дневника. И теперь у них были одни четверки и пятерки! И стали все отличными врачами, учителями, певцами, поварами, летчиками и космонавтами! А кем хочешь стать ты? Будешь ли ты хорошо учиться, чтобы тобой можно было всем гордиться?!
ДВОЙКА – ЛЕБЕДЬ
У реки в бору плакала Двойка. Она боялась войти в реку, потому что не умела плавать. К ней подошла цифра Один и сказала ей:
— Не грусти подружка! А потом к ней подошла цифра Три и сказала ей:
— Вытри слёзки! Последние к ней подошли Четвёрка с Пятёркой и стали её утешать: — Ты на лебедя похожа, значит плавать, можешь тоже! Двойка радостно вздохнула, шеей длинною качнула, в воду зашла и как настоящий лебедь поплыла. На берегу за неё радовались Единица с Тройкой и Четвёрка с Пятёркой.
ДРУЖБА КРЕПКАЯ
В далёкой, далёкой стране Цифландии жили — были разные цифры. Однажды встретились две из них «единица» и «пятёрка». Единица была очень гордая, высокая, всегда ровно держала спину и очень любила с кем – ни будь поспорить. Пятёрочка была весёлая, яркая, но очень большая зазнайка. И затеяли они спор кто из них больше и важнее. «1» — говорит: я выше, а значит я больше! «5» — ей отвечает: а я больше места занимаю на тетрадном листе, значит я больше! Спорили они долго и никак не могли разобраться кто же из них больше, тогда решили «1» и «5» отправиться за советом к другим цифрам. Пришли они, но тем было некогда. И лишь только «нуль» сказал – все цифры важны! Ты единица делаешь другие цифры десятками, и ты самая первая из всех цифр. А ты Пятёрочка больше и ставишь детям в школе хорошие оценки. Если встанете вы рядом, то станете одной цифрой. Обрадовались «1» и «5» подошли друг к другу взялись за руки, и получилась цифра «15» Так и стали они неразлучные друзья!!! Всегда и везде вместе!
МАТЕМАТИЧЕСКИЙ ТЕРЕМОК
Как-то рано поутру шла Однёрка по столу, а на том столе лежала книга безымянная. Захотелось ей поспать на её мягоньких листах – белоснежных простынях. Постучала, всё молчат, значит тут и буду спать. Мимо лебедем плыла цифра Два из далека, увидала нашу книгу и обрадовалась та, заживу в ней навсегда. Тук, тук, тук кто здесь живёт? — Это я Единичка, тонкая как спичка. — А я цифра Два словно лебедь и красива, и стройна. — Заходи, коль ты пришла, вместе жить будем тогда. И скакала рядом Тройка та, что прыгает так бойко, постучала и она, вы впустите жить меня. Так собрались в нашей книжке цифры все, какие есть, мы сейчас их перечислим: Тут Четыре — руки в боки, Пять — что любит поиграть, А Шестой – тот лежебока, очень любит крепко спать, Тут и Седьмой – его зовём мы кочергой, А Восьмёрка – два кружка, как сестра снеговика, И Девятый – самый старый весь седой и с бородой. Не хватало лишь Ноля, не заставил себя ждать тот, кряхтя, не торопясь с боку на бок волочась. Ну а как же так друзья без названия она, наша книга, что собрала всех с Девятки — до Ноля? Ты учись скорей считать и тогда ты будешь знать, называется она Математика друзья!!!
ЗАЯЦ ПО ИМЕНИ НОЛИК
Шёл по лесу заяц по имени Нолик. Шёл он один, потому что семьи у него не было. Но он очень хотел жить в уютном домике со своей семьёй. На встречу по тропинке бежала зайчиха по имени Единичка. Нолику очень понравилась единичка и он предложил ей построить домик и жить в нём. Вот и стали они жить вместе. Дом был красивый и уютный, а вокруг него большой и крепкий забор, чтобы волк не мог к ним пробраться И появились у них 9 замечательных зайчат: Двойка, Тройка, Четверик, Пятёрочка, Шестерик, Семёрик, Восьмёрочка, Девяточка и Десяточка.
ВЕСЁЛЫЙ СВЕТОФОР
Жил — был весёлый светофорик. Он стоял на перекрёстке. Но однажды он заболел и сломался, и у него погасли все 3 огонька: красный, жёлтый и зелёный. Мимо проходила девочка, она позвонила в службу спасения цифре 3.
Цифра принесла светофору волшебное печенье. Оно было разного цвета и разной формы. Красное печенье было треугольное, жёлтое печенье квадратное и зелёное печенье было круглым. Когда светофор съел печенье, то его огоньки снова заработали. Но теперь они были разной формы, от этого он смотрелся ещё веселее.
ВОЛШЕБНАЯ ПЛАНЕТА МАТЕМАТИКИ
Жила-была одна девочка, её звали Настя. У неё были квадратные зайчики, жили они все на волшебной планете, где всё было розовое и море, и лес, и горы. Когда Настя искупалась в волшебном море, то она тоже стала розовой. Она спросила у зайчиков: «Почему я розовая?» Но они не могли ей ответить. И пошли они все к русалочке по имени Ариэль, чтобы она ответила им на все их вопросы. Она была странная, совсем круглая, как шар. Ариэль сказала, что планета, на которой они живут, волшебная и занимательная. Потому что все жители планеты любят загадывать друг другу загадки-шутки по математике, а так как они очень весёлые и смешные все жители веселятся и радуются и от этого всё вокруг становиться розовым и красивым. И Ариэль стала загадывать свои загадки: Задумай число до 5. Прибавь к нему 2, а я отгадаю, какое число ты задумал. Сколько у тебя получилось? Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей. Курица, стоящая на одной ноге, весит 2 кг. Сколько весит курица, стоящая на двух ногах? (2 кг) Настя и её квадратные зайчики долго слушали русалочку. Ведь загадок было так много, что они не заметили, как настал вечер. А закат на планете тоже был розовым — это было так красиво. А потом все ушли спать в свои домики розового цвета. И им всю ночь снились только розовые сны.
Вот и сказочкам КОНЕЦ, а кто ответил МОЛОДЕЦ!
Сказка «Город геометрических фигур»
Чтобы сделать урок еще интереснее, можно рассказать о приключениях любимых героев детей в городе, где живут геометрические фигуры. Например, можно рассказать сказку про Чипа и Дейла.
Как-то раз бурундучки, когда еще не стали знаменитыми сыщиками, забрели в неизвестный им город. В то время землю окутал снег, и, конечно же, Чипу и Дейлу пришлось искать себе дупло потеплее. Но как оказалось, найти домик не так сложно, как сделать его уютным.
И пошли бельчата к известным мастерам, чтобы попросить сделать им дверь для дупла. Первым их встретил напыщенный Треугольник. Он всегда думал, что только его фигура является идеальной и поэтому сделал дверь по своему подобию — треугольной. Но сколько бельчата не старались, закрыть дупло не получилось.
Тогда Чип отправился к Овалу. Этот мастер знал, что каждая фигура хороша по-своему, поэтому не стал делать овальную дверь. Она бы ну никак не поместилась в дупло. Вырезав круг, Овал отнес его к Чипу и Дейлу и закрыл продуваемую дыру.
Так Треугольник понял, что каждая фигура в этом мире очень важна.
«Гуси-лебеди»
Жили-поживали дед да баба. Были у них сын и дочка. Ушли они как-то на работу, а дочери наказали за братцем следить. Как только родители покинули отчий дом, девочка забыла о наказе, посадила братика на солнышко, а сама убежала играть с подружками. Вернувшись, она не обнаружила братца, его унесли гуси-лебеди. Поплакала Алена, а потом побежала искать малыша. На пути ей встретилась печка, которая обещала указать дорогу в ответ на правильно решенную задачку про пирожки.
Побежала Аленка по тропинке, на ее пути встретилась яблоня.
Чтобы та указала ей путь к гусям-лебедям, девочке пришлось найти среди фигур круги (ребята помогают сделать правильный выбор).
Яблоня сказала, что братец Иванушка живет в избушке Бабы-Яги. Вошла девочка в избу и говорит: «Здравствуй, бабушка Яга. Отдай мне, пожалуйста, моего младшего братика».
Яга попросила навести порядок в избе, разложив вещи по следующим признакам:
- по названию: чашки, тарелки, мячики, кружки;
- по размеру;
- по цвету;
- по форме.
Алена с помощью школьников быстро решает задачу Яги и возвращается вместе с братом домой.
Домашнее задание
Помимо того, что ребятам можно рассказывать сказки, можно попросить их самих придумать истории. Это поможет еще больше понять разницу между фигурами. Разделив детей на группы, можно дать тему, например «Сказка о бароне Квадрате», которую они придумают сообща прямо на уроке. Детям будет проще придумывать историю, если дать им фабулу. Поэтому в качестве начала сказки можно предложить использовать несколько вводных предложений: «Как-то раз в волшебную страну, где правила царица Математика, пришел Лист. Его края были неровными, потому что нерадивый учение вырвал его из тетради. Чужестранец очень страдал из-за этого и считал себя некрасивым. Дни и ночи напролет он лил горькие слезы. И тогда царица Математика издала указ. Она пообещала дать титул барона тому, кто сможет помочь горю Листа…».
Конечно, рассказы, придуманные учениками, могут быть однотипными, но это неважно. Самое главное — процесс, в который будет погружен ребенок. Но перед тем как давать подобные задания, лучше рассказать сказку, в которой будут описаны свойства всех фигур.
Тип: комбинированный, с применением
компьютерных технологий.
Цели и задачи.
Образовательные – познакомить учащихся с
историей возникновения геометрии, с первыми
основными геометрическими понятиями: точка и
прямая, «лежать между» («лежать на») для точек
прямой, с их условными обозначениями; с
простейшими геометрическими фигурами на
плоскости.
Развивающие – развивать творческую и
мыслительную деятельность учащихся на уроке с
помощью решения задач исследовательского
характера, интеллектуальные качества личности
школьников такие, как самостоятельность,
способность к оценочным действиям, обобщению,
быстрому переключению; способствовать
формированию навыков самостоятельной работы;
формировать умение четко и ясно излагать свои
мысли.
Воспитательные – прививать учащимся интерес
к предмету с помощью изучения истории и развития
науки, применения информационных технологий (с
использованием компьютера); формировать умение
аккуратно и грамотно выполнять математические
записи.
План урока:
- Вводное слово учителя с показом слайдов.
- Рассказ учителя об истории развития геометрии с
показом слайдов. - Выделение основных понятий планиметрии.
- Повторение ранее изученного геометрического
материала, математических символов и выполнение
учащимися задания на взаимное расположение
точек и прямых на плоскости. - Самостоятельная работа в виде тестирования с
последующей самопроверкой (слайды с ответами и
критерием оценивания). - Проверка усвоения изученного материала в форме
кроссворда. - Подведение итогов урока. Выставление оценок.
Домашнее задание.
Ход урока
1. Вводное слово. В начале XX века великий
французский архитектор Ле Корбюзье сказал: «Я
думаю, что никогда до настоящего времени мы не
жили в такой геометрический период. Все вокруг –
геометрия».
Эти слова очень точно характеризуют и наше
время. Мир, в котором мы живем, наполнен
геометрией домов и улиц, гор и полей, творениями
природы и человека. Лучше ориентироваться в нем,
открывать новое, понимать красоту и мудрость
окружающего мира поможет вам предмет –
геометрия, который мы начинаем изучать с этого
урока.
Внимательно прочитайте тему урока, вдумайтесь
в ее формулировку, сформулируйте вопросы, на
которые мы должны, на ваш взгляд, найти ответы в
ходе урока.
Учащиеся называют вопросы, а учитель обещает,
что на все вопросы мы все сообща постараемся
найти ответы на этом уроке.
Вопросы:
Что означает слово «геометрия»?
Когда, как и с какой целью зародилась наука –
геометрия?
Кого можно считать основоположниками
геометрии? Как называлось первое дошедшее до нас
научное изложение геометрии?
Какие можно выделить этапы развития геометрии?
Что изучает геометрия?
Как можно объяснить, что такое точка, прямая, отрезок?
Различные математические объекты определили
направления в математике.
С геометрическими понятиями вы уже знакомы с
самого детства: круг, квадрат, угол, куб,
измерение отрезков, площадь, объем, и т.д.
При изучении фигур в геометрии не берется во
внимание, из какого материала они сделаны, какого
цвета, в каком состоянии находятся (твердое,
жидкое, газообразное).
Этим занимается физика, химия, биология. Изучая
геометрию, нас будут интересовать формы и
размеры предметов.
Шкаф, спичечный коробок, кирпич, многоэтажный
дом – прямоугольный параллелепипед.Футбольный мяч, резиновый мяч, мыльный пузырь –
шар.Блин, солнце, луна, озеро – круг.
Красный кубик, синий кубик, зеленый кубик – куб.
Таким образом, геометрическая фигура (тело)
– это абстрактный предмет, в котором
рассматривается только форма и размер, не
обращая внимания на физические свойства.
Расположением геометрических фигур занимаются
различные разделы геометрии.
Слайд 1
Слайд 2
Геометрические фигуры, точки которых лежат в
одной плоскости, изучает планиметрия.
Геометрические фигуры, точки которых не лежат в
одной плоскости, изучает стереометрия.
Мы начнем изучать геометрию с плоских фигур.
Но прежде заглянем в историю возникновения
геометрии.
2. История возникновения геометрии.
Великий немецкий математик Вильгельм Лейбниц
сказал: «Кто хочет ограничиться настоящим, без
знания прошлого, тот никогда его не поймет».
Заглянем в прошлое, когда зародилась наука
геометрия….
Для первобытных людей важную роль играла форма
окружавших их предметов. По форме и цвету они
отличали съедобные грибы от несъедобных,
пригодные для построек породы деревьев от тех,
которые годятся лишь на дрова, вкусные орехи от
горьких и т.д. Особенно вкусными казались им
орехи кокосовой пальмы, которые имеют форму шара.
А добывая каменную соль, люди наталкивались на
кристаллы, имевшие форму куба. Так, овладевая
окружающим их миром, люди знакомились с
простейшими геометрическими формами.
Уже 200 тысяч лет тому назад были изготовлены
орудия сравнительно правильной геометрической
формы, а потом люди научились шлифовать их.
Специальных названий для геометрических фигур,
конечно, не было. Говорили: «такой же, как
кокосовый орех» или «такой же, как соль» и т.д.
Слайд 3
А когда люди стали строить дома из дерева,
пришлось глубже разобраться в том, какую форму
следует придавать стенам и крыше, какой формы
должны быть бревна. Сами того не зная, люди все
время занимались геометрией: женщины,
изготавливая одежду, охотники, изготавливая
наконечники для копий или бумеранги сложной
формы, рыболовы, делая такие крючки из кости,
чтобы рыба с них не срывалась.
Когда стали строить здания из камня, пришлось
перетаскивать тяжелые каменные глыбы. Для этого
применялись катки. И заметили, что перекатка
проще, если взять кусок дерева с почти одинаковой
толщиной в начале и в конце. Так люди
познакомились с одним из важнейших тел – цилиндром.
Скалками цилиндрической формы пользовались и
женщины, раскатывая белье после стирки.
Перевозить грузы на катках было довольно
тяжело, потому что сами древесные стволы весили
много. Чтобы облегчить работу, стали вырезать из
стволов тонкие круглые пластинки и с их помощью
перетаскивать грузы. Так появилось первое
колесо.
Но не только в процессе работы знакомились люди
с геометрическим фигурами.
Слайд 4
Издавна они любили украшать себя, свою одежду,
свое жилище (бусинки, браслеты, кольца, украшения
из драгоценных камней и металлов, роспись
дворцов).
Для того, чтобы взимать налоги с земли,
необходимо было знать их площадь. Гончару
необходимо было знать, какую форму следует
придать сосуду, чтобы в него входило то или иное
количество жидкости. Астрономы, наблюдавшие за
небом и дававшие на основе этих наблюдений
указания, когда начинать полевые работы, должны
были научиться определять положение звезд на
небе. Для этого понадобилось измерять углы.
Так практическая деятельность людей привела к
дальнейшему углублению знаний о формах фигур,
развитию геометрии. Люди стали учиться измерять
и площади, и объемы, и длины и т.д.
Древние египтяне были замечательными
инженерами. До сих пор не могут до конца
разгадать загадки огромных гробниц Египетских
царей – Фараонов.
Слайд 5
Пирамиды – а они построены более 5 тыс. лет
назад – состоят из каменных блоков весом 15 тонн,
и эти «кирпичики» так подогнаны друг к другу, что
не возможно между ними протиснуть и почтовую
открытку. А при строительстве использовали лишь
простейшие механизмы – рычаги и катки.
«Все боится времени, но само время боится
пирамид».
В Вавилоне при раскопках ученые обнаружили
остатки каменных стен, высотой в несколько
десятков метров, а высота Вавилонской башни
достигает 82 метра.
Слайд 6
Без математических знаний все эти сооружения
невозможно было бы построить. И все же
математические знания египтян и вавилонян были
разрозненные и представляли собой свод правил,
проверенных практикой, поэтому правила надо было
зазубривать, не понимая, почему надо применять
то, а не другое.
Слайд 7
Почти все великие ученые древности и средних
веков были выдающимися геометрами. Девиз древней
школы был: «Не знающие геометрии не
допускаются!»
Слайд 8
Слайд 9 (Пифагор VI век до н.э., основал свою
школу)
Настает время привести все разрозненные знания
в систему.
И наиболее удачно была изложена геометрия, как
наука о свойствах геометрических фигур,
греческим ученым Евклидом (III в. до н. э.) в
своих книгах «Начала». Произведение состояло из
13 томов, описанная в этих книгах геометрия
получила название Евклидова.
Слайд 10
Конечно, геометрия не может быть создана одним
ученым. В работе Евклид опирался на труды
десятков предшественников и дополнил работу
своими открытиями и изысканиями. Сотни раз книги
были переписаны от руки, а когда изобрели
книгопечатание, то она много раз переиздавалась
на языках всех народов и стала одной из самых
распространенных книг в мире.
Слайд 11
В одной легенде говорится, что однажды
египетский царь Птолемей I спросил
древнегреческого математика, нет ли более
короткого пути для понимания геометрии, чем тот,
который описан в его знаменитом труде,
содержащемся в 13 книгах.
Ученый гордо ответил: » В геометрии нет
царской дороги«.
В течение многих веков «Начала» были
единственной учебной книгой, по которым молодежь
изучала геометрию. Были и другие. Но лучшими
признавались «Начала» Евклида. И даже сейчас, в
наше время, учебники написаны под большим
влиянием «Начал» Евклида.
Несмотря на то, что содержание геометрии
расширилось далеко за пределы учения о земле, она
по-прежнему продолжает называться «Геометрией».
3. Основные понятия планиметрии
Конечно, геометрия дает не только
представление о фигурах, их свойствах, взаимном
расположении, но и учит рассуждать, ставить
вопросы, анализировать, делать выводы, то есть логически
мыслить.
Мы начинаем изучать планиметрию.
Как вы думаете, какие самые основные понятия
планиметрии?
Даже самое большое здание складывается из
маленьких кирпичей, так и сложные геометрические
фигуры составляются из простейших фигур.
Конечно, самая главная — это точка.
Слайд 12
Почти все названия геометрических фигур
греческого происхождения, как и само слово
геометрия. Однако эти слова вошли в русский язык
не непосредственно с греческого, а через
латинский язык.
Точка – результат мгновенного касания, укол
Отсюда же произошел медицинский термин пункция-прокол.
Пунктир.
Линия – льняная нить.
Линолеум – первоначально означал промасленное
льняное полотно.
Как уже было сказано ранее, все названия
геометрических фигур первоначально были
названиями конкретных предметов, имеющих форму,
более или менее близкую к форме данной фигуры.
4. Повторение известного материала о точках и
прямых и их расположении относительно друг
друга.
Давайте вспомним, как обозначают на чертеже
прямые и точки.
— Прямая безгранична, поэтому на чертеже
изображают часть.
— Прямые обозначают двумя заглавными
латинскими буквами, соответствующим двум точкам
на прямой или одной малой буквой.
— Точки обозначают заглавными латинскими
буквами.
— Знак означает принадлежание, т.е. А1
m
означает, что точка А1 принадлежит прямой m
или лежит на ней. И А2m соответственно, не
принадлежит или не лежит.
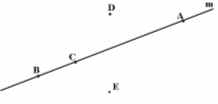
Выполнить задание
Слайд 13
Опишите этот рисунок. Запишите рассказ,
используя условные обозначения.
5. Самостоятельная работа.
В форме теста.
Самопроверка теста, выставление оценок.
Слайд 14 (ответы)
Слайд 15 (Критерий оценивания)
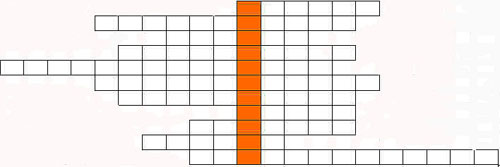
6. Проверка усвоения изученного материала.
Учитель выдает кроссворд каждому ученику.
Кроссворд
Слайд 16
- Вставь пропущенное слово: «Через любые две
точки можно провести … ; и при том только одну». - Математический знак
- Название книги, в которой впервые был
систематизирован геометрический материал. - Геометрическая фигура на плоскости.
- Геометрическая фигура в пространстве.
- Раздел геометрии.
- Математический знак
- Первоначальное понятие в геометрии.
- Часть прямой, ограниченная двумя точками.
- Древнегреческий математик.
- Геометрическая фигура на плоскости.
Если кроссворд учащиеся не успевают выполнить
весь, то он выдается на дом для доработки, и
следующий урок начинается с опрашивания по
вопросам кроссворда. Или: тот, кто успел ответить
на все вопросы кроссворда вовремя, считается
полностью усвоившим урок.
Итак, что же получилось в выделенной части?
Слайд 17
Что такое планиметрия?
7. Подведение итогов урока.
На все ли вопросы вы получили сегодня ответы?
(Учитель обращает внимание учащихся на вопросы,
поставленные в начале урока, и просит кратко еще
раз на них ответить.)
Выставление оценок за тест.
Домашнее задание: стр. 3-6, № 1,2 на стр.7
Использованная литература:
- Атанасян Л.С. и др. Геометрия 7-9. М.:
Просвещение, 1991. - Депман И.Я., Виленкин Н.Я. За страницами учебника
математики. Пособие для учащихся 5-6 класса. М.:
Просвещение, 1989. - Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная
геометрия. Учебное пособие для 5-6 классов.
Смоленск: Русич, 1995. - Геометрия 7 класс. Поурочные планы по учебнику
Атанасяна Л.С. и др. «Геометрия. 7-9
классы»./Авторы-составители Афанасьева Т.С.,
Тапилина Л.А. – Волгоград: Учитель, 2002. - Энциклопедия для детей. Том 11. Математика. – М.:
Аванта +, 1999. - Чупин В.Д. От Пифагора до наших дней. Пермь, 1992
- Методические рекомендации по курсу «История
математики» ПГПУ. Пермь, 2004. - Мищенко Т.М. Геометрия. Рабочая тетрадь для 7
класса. М.: ИД Генжер, 1998.
Презентация к уроку
Действующие лица: король Многоугольник XII; королева Окружность; принцесса Прямая; принц Отрезок; Герцог Угол и его сыновья: углы Развернутый, Прямой, Острый, Тупой; графиня Биссектриса; графиня Медиана; баронесса Точка; Треугольник- разбойник; фея утверждений Аксиома; фея доказательств Теорема.
Автор.
В царстве Геометрическом, городе Планиметрическом
Правил король Многоугольник XII.
Его поприветствовать стоит овацией.
Супруга его, королева Окружность,
Имела весьма недурную наружность.
А это дочка — принцесса Прямая. Теперь же сына я представляю: Зовут симпатичного принца Отрезок. Он весел и мил» хоть бывает и резок. Представлена вам вся семья наконец. Давайте заглянем теперь во дворец. Во дворце сегодня бал, Тьму гостей король созвал: Нынче юная принцесса — именинница. Вот в роскошнейшей карете Герцог Угол в гости едет.
Угол. Спешу я вас поздравить, принцесса, поскорей. Позвольте вам представить красавцев-сыновей: Вот угол Развернутый, этот Прямой, А вот угол Острый, а это Тупой. Прямая.
Ах, знакомство мне приятно, только очень непонятно: Как их можно различить, как не спутать, не забыть?
Угол. Их запомнить очень просто:
Угол меньше девяносто у меня зовется Острым. Тот, что равен девяносто, называется Прямым, А Развернутый средь прочих Самым выглядит большим, Ста восьмидесяти равна у него величина.
Автор. У крыльца остановился новенький кабриолет И графиня Биссектриса вышла. Ну а ей вослед (Слышишь, грохот барабана?) Мчит графиня Медиана.
Биссектриса. Принцесса, мы вас поздравляем! Медиана. И счастья в жизни вам желаем! Принцесса. Спасибо! Рада видеть вас!
Как дома будьте вы у нас!
Графини отходят. Принцесса (сама себе).
Ах, нет милей графинь двоих! Но я так мало знаю их! Мне их узнать поближе б надо. Пойду поспрашиваю брата. (Подходит к Отрезку.)
Отрезок, милый, объясни ты, Чем те графини знамениты, Насколько знатны и богаты? Отрезок. Сестрица, знать давно должна ты, Что Медиана мне родня, Похожа в чем-то на меня. Но есть и разница со мной: Она отрезок не простой, А в треугольнике вершину Соединивший с серединой Той, что напротив, стороны. Быть осторожны мы должны…
Принцесса. Ах, Боже мой, как это странно!
Позор! Графиня Медиана Имеет связи с Треугольником, Известным в городе разбойником. Ну а графиня Биссектриса?
Отрезок. Да мерзопакостная крыса!
Она шныряет по углам И делит их напополам.
Биссектриса (шепотом).
Ах, обозвал меня он крысой! Ну, он попомнит Биссектрису! Чуть позже месть устрою я Всему семейству короля.
Автор. Наконец-то прибыла баронесса Точка.
Свой подарок поднесла королевской дочке. (Точка подходит к принцессе, вручает подарок, делает реверанс, отходит.)
Вот чудесно, бал в разгаре, Все танцуют, все в ударе!
(Музыка, танец геометрических фигур.)
Король. Вот исполнилось принцессе 18 лет с утра.
Стала совершеннолетней, замуж ей теперь пора.
Угол. Ваше высочество, Многоугольник XII,
Очень мне хочется, позвольте признаться, На милой красавице, дочке твоей, Женить одного из своих сыновей. Но старший мой сын уж женат, к сожаленью, А из остальных на свое усмотренье Вы выбрать смогли б, несомненно, любого: Тупого, иль Острого, или Прямого. Король. О, герцог! Вам мое почтенье! Благодарю за предложенье. Но хочу отметить я, как красива дочь моя: Тонка, стройна, бесконечно длинна. Ей, такой прямой и стройной, Надобен супруг достойный. Потому для всех, кто просит руку дочери моей, Объявить хочу я конкурс. Претенденты, ну, смелей! Кто из вас умнее прочих, очень хочется узнать. Без ошибок на вопросы вы должны мне отвечать. (Лицом в зал.)
Ну а зрителей попросим
Мы ответы подтверждать или опровергать.
Вот услышали ответ и кричите «Да!» иль «Нет!».
Вопрос; Какие существуют в геометрии фигуры, Приведите мне пример?
Тупой угол. Ферзь и пешка, например.
(Зрители: «Нет!»)
Прямой угол. Треугольник, например.
(Зрители: «Да!»)
Острый угол. Луч, отрезок, например. (Зрители: «Да!») Король. Отвечайте сей же час: Пересечься сколько раз Две различные прямые Могут в плоскости у нас?
Тупой угол. Я скорей ответить жажду: Пересечься могут дважды.
Прямой угол. Бесконечно много раз
Пересечься могут, да-с. Острый угол. Если речь о двух прямых, Точка общая у них Может — я прошу понять — Лишь одна существовать. Или вовсе ее нет. Вот вам правильный ответ.
Король. И еще вопрос вам всем: Ну а если нет совсем Общей точки у прямых? Как же назовем мы их?
(Тупойугол пожимает плечами.)
Прямой угол. Вопрос простой, чего уж думать тут
Их перпендикулярными зовут.
Острый угол. Если прямые не пересекаются,
Они параллельными называются.
Король. Вижу я, что угол Острый Ум имеет самый острый. Мне такой подходит зять! Дочь ему готов отдать. Автор. Вот уже и поздний вечер.
Бал окончен, гаснут свечи. Надо вам напомнить здесь Про обещанную месть. Ну, про ту, что Биссектриса Обещала произвести. Возвращаясь из гостей, Биссектриса поскорей Мчит за город, к лесу Карандашному, К Треугольнику-разбойнику страшному. Суть беседы их полночной Не известна никому, Но несчастью завтра точно В королевском быть дому… Вот и утро. Весь народ Весть дурную узнает: Без следа исчезла в ночь Из дворца принцесса-дочь. Плач и траур во дворце, Изменились все в лице. У отца печаль в глазах, Королева вся в слезах.
Король. Кто сумеет нам помочь?
Королева. Кто вернет нам нашу дочь?
Автор. К счастью, есть на свете чудо. Вдруг неведомо откуда Феи в замке появились.
Король. Кто вы? И зачем явились?
Феи (по очереди представляются, слегка приседая). Фея утверждения Аксиома, фея доказательства Теорема.
Аксиома. Мы готовы вам помочь.
Знаем мы, где ваша дочь. Теорема. Прямую похитил разбойник, Унес ее в лес Треугольник. Аксиома. Мы мигом его вам доставим,
Принцессу вернуть вам заставим.
Теорема взмахивает волшебной палочкой. Вбегает Треугольник, падает на колени перед королем, истошно вопит.
Треугольник.
Не вели меня казнить! Умоляю пощадить! Приказала Биссектриса похищенье совершить. Я верну вам вашу дочь, уберусь из царства прочь, И не сделаю вреда я вам больше никогда. Только не губи, прости! На свободу отпусти!
Король. Я в прощении отказываю, Наказать его приказываю! Голову ему срубить, В трапецию превратить! А графиню Биссектрису надо тоже наказать: Мы ее отправим в угол, Чтоб всю жизнь ей там стоять!
Теорема взмахивает волшебной палочкой. Появляется принцесса Прямая. Всеобщее ликование.
Автор. Ну вот, с Многоугольником XII И всей его семьей пора прощаться нам. Всего два дня мы с ними провели, Но пользы они много принесли. Ведь признаки фигур геометрических Теперь, надеюсь, знаете отлично вы.
В 7 классе ученики начинают изучать новый предмет — геометрию. До этого они уже знакомились с некоторыми геометрическими понятиями, но не так подробно. Чтобы в дальнейшем не возникали трудности с усвоением информации, следует с самого начала усвоить основные моменты: уметь различать типы фигур, знать основные их свойства, выучить теоремы, признаки фигур. В 7 классе изучаются простейшие объекты: точка, луч, отрезок, прямая и т.д. Кроме этого, в учебниках подробно рассматривается треугольник.
Чтобы помочь ученику с усвоением основных тем по геометрии, ниже рассмотрено их содержание, представлены рисунки фигур и задачи по темам треугольников.
Основные темы по геометрии 7 класс
Ученику 7 класса предстоит познакомиться со следующими основными разделами учебника по геометрии:
-
Начальные сведения (об основных геометрических объектах).
-
О треугольниках: что это, какие бывают, как понять, равны ли два треугольника.
-
Отдельно о равнобедренном и прямоугольном треугольнике.
- Задачи по пройденному материалу.
Геометрия 7 класс объяснение основных тем, понятно для детей
первые геометрические объекты
Начать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.
Первыми геометрическими фигурами, которые стоит усвоить, являются точка, прямая, отрезок.
Точка — это абстрактный объект в пространстве. Никаких измерительных характеристик она не имеет (но можно определить координаты).
Через две точки можно провести прямую линию (причем единственную); она не искривляется, не имеет конца и начала, продолжается до бесконечности.
Иными словами, прямая — это множество точек на одной линии, продолжающееся до бесконечности.
Запомните важную аксиому:
Если часть прямой линии ограничить точками, получится отрезок. У отрезка есть и начало, и конец. Обозначается он большими буквами (например, отрезок КL, SD, AB и т.д.).
Если две прямые пересекаются под углом 90º, то говорят, что они перпендикулярны.
Если прямую ограничить только одной точкой, то получится два луча. У луча есть начало, а конца нет (уходит в бесконечность). Называют луч двумя буквами, например, ОА.
Еще одна фигура — угол. Он представляет собой точку и два луча, исходящие из нее. Лучи — это стороны угла, а начало этих сторон — его вершина. От того, сколько градусов составляет угол, зависит тип треугольника, который можно образовать.
О равных треугольниках. Равнобедренный треугольник
Треугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.
Сумма всех углов в треугольнике равняется 180º. Знание этого факта пригодится при решении задач на нахождение углов.
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.
Если один треугольник (назовем его CFD) наложить на другой (C1F1D1) и они будут соответствовать друг другу, то треугольники равны. У равных фигур все элементы равны.
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.
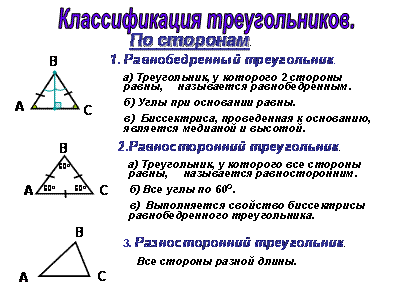
Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.
На заметку! Если равны все стороны, а не только две, то треугольник уже равносторонний, а не равнобедренный.
Исходя из этого, можно выделить признаки равнобедренного треугольника. Треугольник равнобедренный, если:
- 2 угла в нем равны;
- биссектриса одновременно является высотой и медианой;
- медиана — биссектриса и высота;
- высота, соответственно — медиана и биссектриса.
Если взять треугольник неравнобедренный, то эти три составляющие (высота, биссектриса и медиана) не будут совпадать (это четко прослеживается на рисунке ниже).
параллельные прямые
Если на тетрадном листе кажется, что прямые параллельны, но имеется небольшой уклон, то вполне вероятно, что за пределами листа (ведь они бесконечны), прямые пересекутся.
Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.
Показать параллельность прямых а и б можно так: а ΙΙ б.
прямоугольный треугольник и его свойства
Прямоугольным называют треугольник, в котором один из углов равен 90º. Рассмотрим название сторон такой фигуры.
Геометрия 7 класс задача по теме треугольники, пояснение решения задач
Решим несколько задач про треугольники:
- нахождение периметра;
- доказательство равенства треугольников.
Чтобы найти периметр в представленной задаче, нашли сперва неизвестные стороны. Потом просто сложили полученные значения.
Для этой задачи понадобилось знание признаков равенства треугольников.
Для решения задачи понадобится знание признаков равнобедренного треугольника. Так, можно утверждать, что в треугольнике сторона АС и АВ равны, как и СМ и МВ. Поскольку периметр — это сумма всех сторон, получается, что сумму периметра АВМ можно записать сложением АВ, ВМ и АМ (ее как раз нужно найти).
Сумму периметра АВС также записали с помощью сложения сторон. Затем упростили это сложение, записав: 32 = 2 АВ + 2 ВМ (так как АВ и АС равны — равнобедренный треугольник; ВМ и СМ тоже равны). Потом эту запись сократили, разделив на 2.
Вышло, что сумма двух сторон равна 16 см. Остается найти третью сторону (АМ). Она входит в треугольник АВМ, периметр которого равен 24 см. Тогда, чтобы найти третью сторону (АМ, нужно просто 24 отнять 16, вышло 8 см. В примере подставили в уравнение, чтобы не запутаться.
Решим задачу на нахождение угла в треугольнике.
Чтобы найти угол С в задаче потребовалось узнать, чему равен угол В. По условиям известно, что внешний В равняется 110º. Знаем, что развернутый угол равняется 180º (это внешний и внутренний угол В в сумме). Поэтому от 180 отнимаем 110. Получается угол В = 70º.
Треугольник равнобедренный, значит углы при основании одинаковые ⇒ угол В = углу А = 70º.
Поскольку сумма углов треугольника равна 180º (по правилу), значит угол С = 180 — углы А и В = 180 — 70 — 70 = 40°.
Задачи на второй и третий признак равенства треугольников подробно представлено в видео-уроке.
Геометрия 7 класс тест по теме треугольник
Закрепим материал по треугольникам, решив несколько тестовых заданий.
- Как называется сумма всех сторон в треугольнике?
а) площадь;
б) периметр;
в) медиана
2. Треугольник называется равнобедренным, если:
а) у него есть основание;
б) все стороны равны;
в) две стороны равны
3. Если в равнобедренном треугольнике к основанию провести высоту, то чем еще она будет являться?
а) биссектрисой;
б) медианой;
в) медианой и биссектрисой;
г) только высотой
4. Сколько всего признаков равенства треугольников?
а) 4;
б) 3;
в) 2
5. В треугольнике можно провести ___ медиан (-ы)
а) одну;
б) множество;
в) три;
г) две
6. Как называются стороны прямоугольного треугольника, которые образуют угол 90º?
а) гипотенузы;
б) катеты;
в) высоты
7. Про что гласит 3-й признак равенства треугольников?
а) про стороны;
б) про сторону и углы;
в) про угол и стороны
8. Под каким углом в любом треугольнике проходит высота?
а) это зависит от вида треугольника
б) под углом 45 градусов;
в) 90 градусов
9. По каким признакам различаются виды треугольников?
а) по размеру сторон;
б) по размеру углов;
в) по размеру сторон и углов;
г) по периметру и площади
10. Чему равна сумма двух острых углов прямоугольного треугольника?
а) 90 градусов;
б) 180 градусов;
в) 60 градусов
Ответы: 1 — б; 2 — в; 3 — в; 4 — б; 5 — в; 6 — б; 7 — а; 8 — в; 9 — в; 10 — а.
7 класс геометрия сложная тема, разъяснить подробно для детей
Решим более сложную задачу, где есть и доказательство равенства треугольников, и поиск углов. Алгоритм решения задачи:
Шаг 1. Начертим, согласно условиям. Дается треугольник АВС, в котором провели медиану (вспоминаем, что медиана делит сторону пополам). В нашей задаче медиана AD уходит за пределы треугольника, создавая дополнительный отрезок DE (он равен AD). Получился треугольник, из которого проведена медиана.
Шаг 2. Первая задача — доказать равенство треугольников ABD и ECD: соединим точку Е и С, чтобы получился треугольник.
Шаг 3. По условиям AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE
Шаг 4. Получается BD = DC, так как медиана разделила BC пополам (выходит, еще одни стороны треугольников равны).
Шаг 5. Рассмотрим углы между сторонами (на рис. обозначены цифрами 1 и 2). Они вертикальные, так как образовались двумя прямыми. Следовательно, они равны.
Из первого признака равенства треугольников знаем, что если 2 стороны и угол между этими сторонами одного треугольника равен этим показателям во втором, то они равные. Пункт а доказан. Переходим к б.
Шаг 1. Нам нужно найти угол АСЕ. Из рисунка видно, что он состоит из 2-х маленьких углов, получается: угол АСЕ равен сумме углов DCA и DCE.
Шаг 2. По условиям мы знаем, чему равен DCA, осталось найти второй. Так как равенство треугольников доказали, значит воспользуемся правилом: напротив равных сторон треугольников лежат и равные углы. AD напротив ABD; DE напротив DCE. Выходит: угол ABD = углу DCE = 40 градусам (по условию).
Шаг 3. Маленькие углы известны, найдем тот, который требуется: угол ACE = 56º + 40º = 96º.
Равенство доказали, угол нашли. Задание выполнено.
Еще пара видеороликов про решение задачи с прямоугольным треугольником, а также вся геометрия за 7 класс в одной задаче.
| 7 класс Геометрия | Учитель : Сейдаметова Г. К. | 10. 02. 2020 г. |
Урок № 42
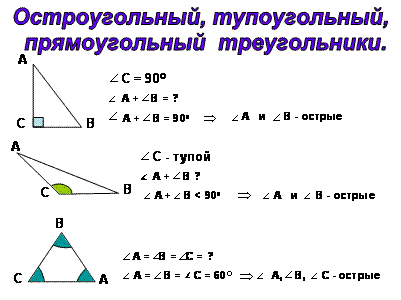
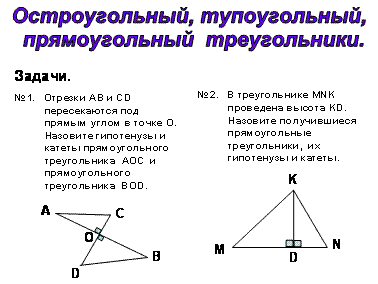
ТЕМА: «Остроугольный, прямоугольный и тупоугольный треугольник. Решение задач»
Тип урока: урок комплексного применения знаний и умений.
Продолжительность урока: 45 минут.
Методы обучения: словесный, наглядный, практический, проблемный.
Цели:
-
повторить и обобщить знания о треугольнике; доказать теорему о сумме углов треугольника и классифицировать треугольники по углам и сторонам; научиться применять полученные знания при решении задач.
-
развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.
-
развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе; содействовать формированию активной жизненной позиции учащихся.
Планируемые результаты:
-
Предметные: уметь в процессе реальной ситуации использовать полученные знания при решении задач
-
Метапредметные: уметь применять свою наблюдательность, геометрическую интуицию и глазомер; формировать коммуникативную компетенцию учащихся; контролировать и оценивать процесс и результаты своей деятельности.
Универсальные учебные действия:
Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий
-
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев
-
Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.
-
Коммуникативные: умеют активно работать на уроке, слушать собеседника и вести диалог, аргументировать свою точку зрения; умеют работать в сотрудничестве с учителем, друг с другом.
-
Личностные: проявляют критичность мышления.
Образовательные технологии, используемые на уроке:
-
информационно-коммуникационная;
-
проблемно-диалоговая технология;
-
здоровьесберегающая технология (физкультминутка, создание позитивного эмоционального настроя на работу всех учеников в ходе урока; организация различных форм деятельности учащихся, организация урока с учетом временного восприятия и усвоения учебного материала).
Формы работы учащихся: фронтальная, индивидуальная.
Методы обучения:
словесные – беседа, рассказ;
наглядные – демонстрация презентации;
практические – решение задач.
Необходимое оборудование и материалы для урока: компьютер, мультимедийный проектор, раздаточный материал.
ХОД УРОКА:
1. Организационный момент. Мотивация урока.
Учитель. Здравствуйте, ребята, садитесь. Я рада встрече с вами. Вижу у вас хорошее настроение, и я желаю всем на уроке подняться еще на одну ступеньку выше в познании.
— Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный нашими предками. Древние греки, на основе наблюдений и из практического опыта, делали выводы, высказывали предположения-гипотезы, а затем на встречах ученых — симпозиумах, эти гипотезы пытались обосновать и доказать. В то время и сложилось утверждение: «В споре рождается истина». Нас сегодняшний урок тоже будет похож на небольшой симпозиум. Мы выскажем своё предположение по вопросу, попытаемся его доказать, и если у нас это получится, то посмотрим, как его можно будет применять при решении задач. А эпиграфом нашего урока, я хочу предложить слова Пифагора:
– Послушайте стихотворение:
Знает даже и дошкольник,
Что такое треугольник,
А уж вам-то как не знать.
Но совсем другое дело –
Быстро, точно и умело
В треугольнике считать:
В нём есть стороны их три
И углов во всех по три
И вершин конечно три.
Если длины всех сторон
Мы сложением найдём
То к периметру придём
Ну, а сумма всех углов
В треугольнике любом
Связана одним числом.
(Учитель держит в руках треугольник) И сегодня мы с вами поговорим о треугольнике, который вдохновлял многих ученых на новые открытия и исследования Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
2. Мотивация, сообщение темы , цели и задач урока.
Наш урок я хотела бы начать со слов математика современности В. В. Произволова:
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»
А сегодня мы продолжим говорить о самой главной фигуре в курсе геометрии 7 класса и это… (треугольник). И сегодняшняя тема, также связана с треугольником.
Чтобы узнать о чем мы сегодня будем говорить, вам предстоит решить несколько задач на нахождение углов треугольника. Найдите угол 1 и заполните таблицу в соответствии с ключом на первой странице маршрутного листа.
Вы получили слово КЛАССИФИКАЦИЯ.
Что такое классификация? Распределение по группам, разрядам, классам.
Где вы встречались с этим словом?
Сегодня на уроке мы выясним, как можно классифицировать треугольники.
3. Актуализация знаний
— Внимание на боковую доску. Здесь даны задачи на готовых чертежах. Вам необходимо их решить.
— Но, прежде один из вас сформулирует теорему о сумме углов треугольника. Другой ученик даст определение внешнего угла треугольника и сформулирует его свойство.
— Контроль за уровнем усвоения изученного материала по теме «Сумма углов треугольника».
Задание №1
1) 2) 3) 4)
Задание № 2: Вычислите градусную величину углов 1 и 2 в каждом из треугольников
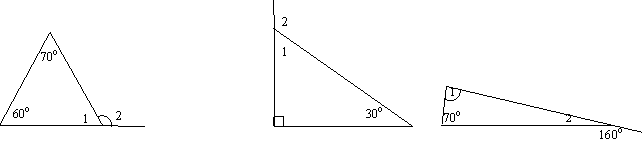
— Актуализация опорных знаний
Для актуализации опорных знаний нужно вспомнить виды углов, их градусные меры и теорему о сумме углов треугольника.
На слайде даны углы, а обучающиеся должны определить их вид.
4. Первичное усвоение новых знаний
— Можно ли по видам углов треугольника определить названия треугольников?
(Выслушиваются варианты ответов учащихся)
Рассматривая треугольники с различными углами, выяснить, что прямой и тупой углы в треугольнике могут быть только по одному, а остальные углы — острые.
— Ребята, попробуйте самостоятельно сделать вывод и сформулировать определение острого, прямоугольного и тупоугольного треугольника.
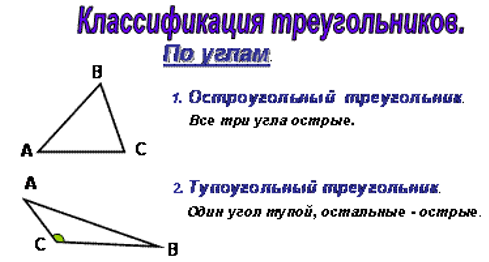
— Итак, дети, мы с вами пришли к такому выводу:
— если все 3 угла треугольника острые, то треугольник называется остроугольным;
— если в треугольнике 1 угол тупой, а 2 других — острые углы, то он называется тупоугольным;
— если в треугольнике 1 угол прямой, то треугольник – прямоугольный.
Вводятся определения остроугольного, тупоугольного, прямоугольного треугольников, понятия гипотенузы и катета прямоугольного треугольника учащимися.
Далее, на слайде показаны верные определения.
Фронтальная работа с классом.
Ученик на доске перемещает слова к треугольникам.
В тетради записать виды треугольников по углам.
— Мы на уроке должны узнать названия сторон прямоугольного треугольника. Итак: две стороны, которые образуют прямой угол, называются катетами; сторона, лежащая против прямого угла, называется гипотенузой.
Вывешиваются на магнитную доску плакаты, на которых нарисованы прямоугольные треугольники. По каждому треугольнику проговариваются названия сторон. Учащиеся перечерчивают к себе в тетрадь.
5. Первичная проверка понимания
Устно решаются задачи на распознавание гипотенузы и катетов.
Классификация треугольников по углам и сторонам. Выделяются основные моменты, связанные с каждым видом треугольника.
Учащиеся сами пытаются классифицировать треугольники по углам и сторонам.
Б) организация проектной деятельности (показ презентаций учащимися)
Обозначается проблема: треугольники можно встретить только на страницах учебников и в школьных тетрадях, или эта фигура в разных видах и разных ролях встречается в окружающем мире?
Для решения этой проблемы разработан информационный минипроект, целью которого является с помощью наблюдения, исследования выяснить, где и как, с какой целью применяются человеком треугольники.
С целью реализации проекта обучающиеся разбились на группы по два человека, определили роли участников (координатор, исследователи, оформитель, ответственный за защиту проекта).
Предлагается на выбор три темы проекта:
Где и как используются треугольники в строительстве, архитектуре.
Где и как используются треугольники в быту?
Где и как используются треугольники в одежде?
6. Первичное закрепление
а) Выписать все равнобедренные треугольники и их элементы (боковые стороны и основание)
б) Выписать все прямоугольные треугольники и их элементы (гипотенузу и катеты)
Два ученика работают у доски – маркером,
остальные – в раздаточном материале.
Самоконтроль.
Проверка.
Один ученик работает у доски, перемещая треугольники, остальные учащиеся работают в раздаточных материалах – вписывают соответствующие номера треугольников
в таблицу.
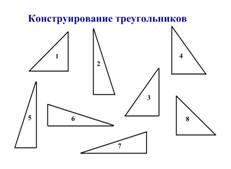
В) Конструирование.
Дано восемь треугольников – четыре треугольника с углами 20 и 70 градусов, два треугольника с углами 45 и 45 градусов, два треугольника с углами 30 и 60 градусов. Перемещая данные фигуры, составить треугольники – равносторонний; равнобедренный тупоугольный; равнобедренный прямоугольный; равнобедренный остроугольный.
Ученики, перемещая треугольники, конструирует на доске, остальные
с моделями на местах.
Самоконтроль.
Проверка.
Г) Динамическая пауза.
Покажите руками развернутый угол, прямой угол, тупой угол, острый угол, углы 45 и 135 градусов
Д) Пиши грамотно.
В геометрические термины, используемые на уроке вписать пропущенные буквы.
Открыть «шторку» и проверить правильность написания.
Один человек работает маркером у доски.
Остальные в раздаточном материале. Самоконтроль.
7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция
Учитель с учениками обсуждают ошибки, сделанные на уроке учащимися.
8. Информация о домашнем задании, инструктаж по его выполнению: п. 32 №223 (б,в);
№227 (а);№230
9. Рефлексия (подведение итогов занятия)
Продолжить фразу. Подвести итог урока.
Ученики, перемещают слова – узнал, удивился, научился, задумался, повторил, запомнил, и устно завершают фразу.
Какие углы называются смежными?
Какие виды треугольников вы знаете?
Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
Какой треугольник называется равнобедренным?
Могут ли быть смежными тупой и прямой углы? Почему?
Какие углы могут образоваться при пересечении улиц?
Приложение
Устный тест
1. В треугольнике АВС угол А равен 90°, при этом другие два угла:
а) один острый, а другой может быть
прямым;
б) оба острые;
в) один острый, а другой может быть
тупым .
2. В треугольнике АВС угол В — тупой, при этом другие два угла могут быть:
а) только острыми;
б) острый и прямой;
в) острый и тупой.
3. В остроугольном треугольнике могут быть:
а) все углы острые;
б) один тупой угол;
в) один прямой угол.
Учитель предлагает обучающимся устно решить задачи по готовым чертежам
-
В треугольнике ABC угол A равен 30o, угол B равен 90o. Найдите угол C.(60)
-
В треугольнике ABC угол C равен 120o, AC = BC. Найдите угол A.(30)
-
В треугольнике ABC угол A равен 40o, AC = BC. Найдите угол C.(100)
-
В треугольнике ABC AC = BC, угол C равен 50o. Найдите внешний угол CBD. (115)
-
В треугольнике ABC угол A равен 40o, внешний угол при вершине B равен 100o. Найдите угол C. (60)
-
В треугольнике ABC AB = BC. Внешний угол при вершине B равен 140o. Найдите угол C.(70)
-
Углы треугольника относятся как 1:2:3. Найдите меньший из них.(30)
-
Для черепичных крыш угол между двумя стропилами берут равным приближённо 90º. Определите, какой высоты будет крыша, если ширина дома 10 м? (5м)
№2 Дано: АВС-
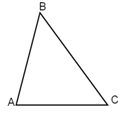
А: В: С = 2:3:4
Найти: А, В, С.
Решение: Пусть одна часть составляет х0. Тогда А=(2х)0,В=(3х)0,С=(4х)0. Зная, что по теореме о сумме углов треугольника А + В+ С=1800, составлю и решу уравнение.
2х+3х+4х=180,
9х=180,
х=20,
А=400, В=600, С=800.
Ответ:400,600,800.
Фронтально:
-
Назовите элементы треугольника:
вершины, стороны, углы.
2. Какой угол называется острым, тупым, развернутым, прямым?
-
Градусная мера острого угла меньше 90 градусов;
-
Градусная мера тупого угла больше 90 градусов, но меньше 180 градусов;
-
Градусная мера прямого угла равно 90 градусов.
3. Свойства смежных углов:
Сумма смежных углов равна 180 градусов.
4. Свойства вертикальных углов:
Вертикальные углы равны.
5. Определение внешнего угла треугольника:
Угол, смежный с углом треугольника.
6. Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
7. Какой треугольник называется равнобедренным,
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине.
8. Как называются равные стороны в равнобедренном треугольнике?
Боковые стороны.
9. Свойство углов у основания равнобедренного треугольника?
Углы при основании равнобедренного треугольника основания равны.
10. Какой треугольник называется равносторонним?
Равносторонний треугольник — это треугольник, в котором все стороны равны между собой по длине.
11. Свойства углов равностороннего треугольника .
Углы равностороннего треугольника равны.
11