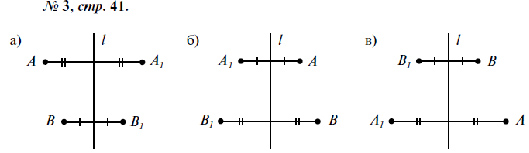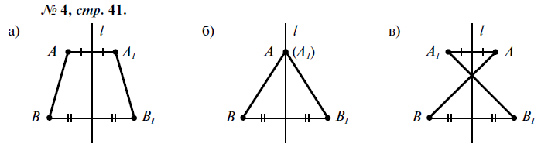что такое симметрия?
15.01.2017
3469
469
Аксберг Татьяна Владимировна
Урок по ИЗО во 2 классе «Что такое симметрия?»
Цель: Уточнить понятие о том, что такое симметрия, симметричные предметы, ось симметрии и научить рисовать симметричную бабочку в технике монотипия
Задачи:
Образовательные: закрепить представление о том, что такое симметрия, ось симметрии, научить видеть симметрию в окружающих нас предметах.
Развивающие: развитие творческих способностей, развитие умения наблюдать, сравнивать, делать выводы,работать с принадлежностями художника.
Воспитательные: воспитание внимательности, усидчивости, аккуратности.
Материалы:
для учителя: образец изделия, шаблоны бабочек, плакаты с изображением симметричных предметов.
для учеников: альбом, простой карандаш, непроливайка, краски и кисти,фломастеры.
Зрительный ряд: иллюстрации, презентация про бабочку.
Ход урока
1.Организационный момент
Быстро прозвенел звонок, Ни минуты не теряем,
Начинается урок. Садимся, слушаем, запоминаем
Сегодня на уроке нам понадобится: альбом, простой карандаш, краски и кисти,фломастеры.
— У всех все есть на партах?
2. Постановка цели
Ребята, давайте вспомним , что такое симметрия? (ответы детей).
3. Беседа по теме урока.
У: Симметрия, ребята, это когда части рисунка или какого – то предмета как бы зеркально отражаются, т.е. левая и правая половинки одинаковы. Линия, которая делит наш предмет пополам, называется осью симметрии.
У: А теперь давайте посмотрим на таблицы. Ребята, посмотрите вокруг, и вы увидите великое множество симметричных предметов. Это листья и цветы, ягоды и фрукты. Оказывается, насекомые, животные и люди тоже симметричны, т.к. их правая и левая половины одинаковы.
У: Ребята, давайте посмотрим на свой класс и найдем симметричные предметы. Назовите их?
Д: Окно, листья у цветов (Учащиеся называют предметы, которые они видят, а учитель поправляет, если ответ неверный).
4.Последовательность выполнения работы
У: чтобы узнать ,что мы будем рисовать,вам нужно отгадать загадку
Спал цветок и вдруг проснулся –
Больше спать не захотел.
Шевельнулся, встрепенулся,
Взвился вверх и улетел (бабочка)
У:-знакомство с видами бабочек.(слайды)
лимонница Это самые ранние бабочки, появляются в начале июля и летают до осени.
капустница Верхняя сторона крыльев густобелая. Вершины передних крыльев черные, а у самки посредине еще два черных пятна. Нижняя сторона задних крыльев желтовато-зеленая с легким темным налётом.Питается всеми видами культур.а не только капустой.
адмирал Ярко-красная полоса проходит по краю крыльев.За эти полоски бабочка и получила своё имя:в старину у адмиралов на брюках были красные лампасы,а через плечо они носили красные ленты.
павлиний глаз встретить можно в лесу-на полянке или опушке,тогда других насекомых ещё очень мало,ранней весной.
махаон Почему бабочка получила такое название – «махаон»? Корни этого имени относят нас в древнюю страну – Трою. Именно там, некогда, согласно легендам, жил чудо-врач Махаон, который умело исцелял раненных воинов.Занесён в Красную книгу.
монарх Бабочки Монархи — короли в мире бабочек.Может прожить от 6 до 8 недель в саду.Ядовита.
-что заметили в окраске?
-какие фигуры можно нарисовать на крыльях?
5.Физминутка
6.Знакомство с техникой монотипииМонотипия — это вид печатной графики.От греческого «моно» — это «один» и «typos» — это отпечаток, образ.Один лист покрывают краской или гуашью, а уже от него делают отпечаток на листе, как правило он неповторимый. Авторство изобретения приписывают итальянскому художнику Джованни Кастильоне (1607-1655).
7.Работа с технологической картой.
Этапы выполнения работы.
2.Согнуть лист пополам.
3.Приложить к сгибу шаблон и обвести его.
4.Развернуть лист и нанесение краски на одну сторону листа.
5.Складываем лист опять пополам. .Прорисовываем недостающие детали.
8. Правила техники безопасности.
У: Но для начала давайте повторим правила техники безопасности при работе с красками.
Как мы работаем с красками?
Д:1. Баночка для воды должна стоять с правой стороны, чтобы не пролить воду на рисунок во время промывки кистей.
2. Нельзя пробовать краски на вкус, это опасно.
3. По окончанию работы нельзя оставлять непромытые кисти.
У: Молодцы, а теперь приступаем к работе.
Практическая работа детей под руководством учителя.
Выполнение работы с опорй на технологическую карту.
Проверка изделия. Оценивание.
У:Поменяйтесь работами с соседом.Проверьте ,правильно ли у него нарисовано(усики,брюшко,крылья ).
Взаимопроверка.
У: Давайте сделаем выставку наших работ на доске и посмотрим, все ли справились с работой. Посмотрите, какие замечательные симметричные бабочки у вас получились. Я довольна вашей работой на уроке.
Итог урока.
Учитель готовит выставку на доске из детских работ.
— Летите бабочки сюда.
— Давайте полюбуемся на ваших бабочек. Какие красавицы!!! Вот прекрасная бабочка с нежными крыльями. А эта очень яркая, как будто на праздник собралась.
— Весной появятся на наших улицах живые бабочки и будут радовать нас своей красотой. А пока пусть эти бабочки украсят наш класс. Откройте конвертик и возьмите только одну бабочку. (Бабочки из цветной бумаги на липкой основе)
Розовую – если очень понравилось сегодня на уроке.
Желтую – если я хотел бы узнать больше.
Голубую – если мне было скучно.
Прикрепите на доску(нарисована цветочная поляна)
-Молодцы ребята, у вас получились прекрасные работы. Мы теперь с нетерпением будем ждать лета, чтобы увидеть живых бабочек
Полный текст материала смотрите в скачиваемом файле.
На странице приведен только фрагмент материала.
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий —
на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
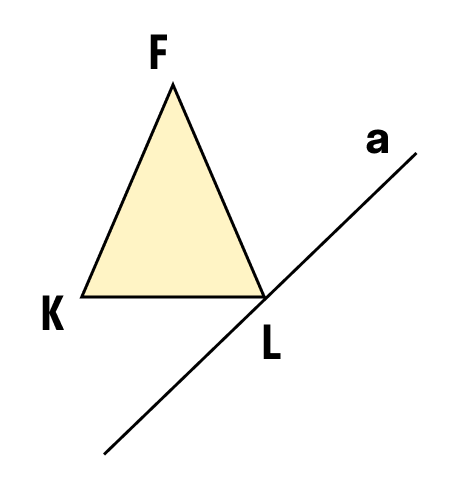
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
СИММЕТРИЯ Руководитель: Пьяникина Н.Н., учитель начальных классов МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 16» ПРОЕКТ учеников 2 «В» класса Саратов 2016 – 2017 г.
2 слайд

Описание слайда:
Мы очень любим рисовать и мастерить. Перед Новым годом мы сделали много снежинок, ёлочек из бумаги и решили украсить ими класс. Трудились дружно, каждый из нас старался прикрепить к стене как можно больше снежинок. Но когда мы посмотрели на свою работу, то поняли, что в ней что-то не так. Снежинки и ёлочки были прикреплены беспорядочно на стене. Мы не могли понять, что же сделали не так? Наша учительница предложила нам выполнить проект «Симметрия».
3 слайд

Описание слайда:
ЦЕЛЬ ПРОЕКТА: выяснить, что лежит в основе красоты окружающего мира; применить знания о симметрии в природе и художественном творчестве в практической работе по украшению класса к Новому году. ЗАДАЧИ: Познакомиться с понятием «симметрия». Научиться находить ось симметрии у различных фигур окружающего мира. Узнать, как художники и народные мастера используют знание симметрии в своей работе. Украсить класс к Новому году, применяя знания симметрии.
4 слайд

Описание слайда:
Симметрия – греч., соразмерность, одинаковость в расположении частей по противоположным сторонам от точки, прямой или плоскости. Словарь С.И.Ожегова
5 слайд

Описание слайда:
Симметрия свойственна природе, она окружает нас на каждом шагу, нужно только внимательно приглядеться. Вот некоторые объекты природы, в которых мы обнаружили симметрию: бабочка,
6 слайд

Описание слайда:
листок, Отражение относительно некоторой линии. Ось симметрии – это прямая линия, по которой можно сложить фигуру. Её половинки совпадут.
7 слайд

Описание слайда:
цветок, Поворот относительно некоторого центра
8 слайд

Описание слайда:
снежинка,
9 слайд

10 слайд

11 слайд

Описание слайда:
человек.
12 слайд

Описание слайда:
Симметрия — это порядок, предсказуемость, устойчивость. Человек любит порядок, предсказуемость, устойчивость, поэтому симметричные объекты кажутся ему красивее. Художники, украшая свои изделия, используют симметрию.
13 слайд

Описание слайда:
Перенос вдоль некоторой линии (ритмическое повторение)
14 слайд

Описание слайда:
На уроках технологии мы научились вырезать симметричные фигуры путём сгиба бумаги. Мы решили украсить класс нашими фигурками ёлочек и снежинок.
15 слайд

Описание слайда:
Мы разделились на группы, и каждая группа придумала, как симметрично расположить фигурки. Работа над эскизом
16 слайд

Описание слайда:
Первая группа украшала классную доску. Ось симметрии проходила по центру доски. На противоположных сторонах от оси симметрии на одинаковом расстоянии расположили снежинки и ёлочки.
17 слайд

Описание слайда:
Вторая группа украшала стену над нашей раздевалкой. Ось симметрии проходила по фигуре Деда Мороза. На противоположных сторонах от оси симметрии на одинаковом расстоянии расположили снежинки, учитывая их размеры.
18 слайд

Описание слайда:
Третья группа украшала стену, применяя прием ритмического повторения.
19 слайд

Описание слайда:
Четвертая группа симметрично расположила наши поделки на окне. Ось симметрии проходит через звездочку. На противоположных сторонах от оси симметрии на одинаковом расстоянии расположили фигурки снеговиков и ёлочки.
20 слайд

Описание слайда:
Симметрия? Что это? — Это не прозвище, Это не имя, не злая болезнь, Это не птица, не зверь, не чудовище, Нельзя это выпить, нельзя это съесть. В симметрии множество тайн и загадок, В ней красота открывается нам. Симметрия- то, что рождает порядок Об этом, дружок, ты задумайся сам. ВЫВОДЫ Симметрия вокруг нас: в природе, в быту, в работах художников и народных мастеров. Симметрия – это красиво. Симметрия – это гармония и красота, равновесие и устойчивость.
21 слайд

Описание слайда:
ИСТОЧНИКИ http://www.uchportfolio.ru/articles/read/1256 Математическая поэзия Словарь ОжеговаС.И. Фотографии http://muzaz.ru/muzaz_song/tosh-levon-madcat-deems-dvatree-jerocrips_babochki.html http://heaclub.ru/images/heaclub/2016/11/23/widescreen-maple-leaves.jpeg http://np174.ru/catalog/kits_for_crafts/mosaic_pictures/mozaichnaja_kartina_milato_n_117_afrikanskaja_romashka_27h20_sm.html?ymclid=836344272031511864600004 http://images.forwallpaper.com/files/images/d/d03c/d03cb4b2/808533/natures-design.jpg http://crosti.ru/patterns/00/13/44/272b65fa46/preview.jpg http://cdn01.ru/files/users/images/b2/7d/b27d00a26f02840ec270b85faaf385da.jpg
-
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта,
Вы можете оставить жалобу на материал.Пожаловаться на материал

- Сейчас обучается 973 человека из 79 регионов

- Сейчас обучается 876 человек из 81 региона

- Сейчас обучается 344 человека из 69 регионов
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-171097
Вам будут интересны эти курсы:
О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Мне кажется, трудно найти человека, который не имел бы какого-то представления о симметрии. Симметрия (от греч. symmetria — соразмерность). Оно, как и слово «гармония», означает соразмерность, наличие определенного порядка, закономерности в расположении частей в природе. Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.
Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать. Свойство симметричности, присущее живой природе, человек использовал в своих достижениях: изобрел самолет, создал уникальные здания архитектуры. Да и сам человек является фигурой симметричной.
Симметрию можно увидеть среди цветов. Осевой симметрией обладают цветки семейства розоцветных, а центральной симметрией – семейство крестоцветных. Симметрию можно увидеть и на листьях деревьев.
Симметрия, характерная для представителей животного мира, называется билатеральной симметрией.
Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет, что всякое твердое тело – кристалл. Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии. (10. с. 21)
Таким образом, данное преобразование фигур (симметрия) вошло в математику в результате наблюдения человека за окружающим миром. Оно встречается часто и повсеместно. Поэтому даже неискушенный человек обычно легко усматривает симметрию в относительно простых ее проявлениях.
Уже в 1 классе начальной школы идет пропедевтическая работа по теме «Симметрия», но без введения данного термина. В подготовительной работе по теме предлагаются задания вида: дорисуй по образцу. (см. приложение). А с преобразованием фигур на плоскости учащиеся знакомятся в 3 классе, эта тема предшествует теме «Симметрия». (7. с. 37. урок 14)
На уроках учащиеся выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представление о преобразовании фигур уточняются. Понятие «преобразование фигур» можно пояснить, как перемещение фигур на плоскости, их перенос. На 14 уроке рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево (параллельный перенос) приложение. С детьми надо проговорить вывод о том, что при таких преобразованиях каждая точка фигур перемещается в одном и том же направлении на одно и то же расстояние. При этом линии, соединяющие соответствующие точки фигур, параллельны. Направление расстояния, на которое осуществляется перенос, удобно показывать направленным отрезком или вектором. (7. с. 37.)
А разговор о симметрии фигур целесообразно начать с практической работы, которую должен выполнить каждый учащийся. Детям, на уроке в 3-м классе я предлагаю выполнить следующее задание: на одной половинке листа бумаги, свернутого пополам ставится чернильная клякса и накрывается другой половинкой. Капля растекается по листу, и если теперь развернуть лист, то получится две фигуры причудливой формы, симметричные относительно линии сгиба. И так, фигуры симметричны относительно прямой L, если они совпадают при перегибании плоскости по этой прямой. (6. с. 244)
Симметричные фигуры можно увидеть проделав другой опыт. Взять какой–нибудь рисунок, положить его на стол, а радом с ним вертикально поместить прямоугольное зеркальце. Тогда в зеркальце появится изображение рисунка, симметричное данному относительно края зеркала.
В окружающем мире дети могут наблюдать симметрию достаточно часто: симметрично расположены глаза и уши человека, дверцы стенного шкафа и т.д. На уроках 15 – 17 учащиеся должны выявить математические закономерности расположения симметричных фигур и в простейших случаях научиться их строить. Для проверки правильности построения используется калька.

Исследование можно организовать в виде практической работы. Если сложить пополам лист бумаги, затем проколоть его ножкой циркуля, то полечатся две симметричные точки. Обозначим их A и B. Что интересного в их расположении?
Для ответа на поставленный вопрос учитель предлагает учащимся провести отрезок AB и обозначить О точку его пересечения с линией сгиба (осью симметрии). С помощью линейки и чертежного угольника дети должны установить, что тока О является серединой отрезка AB, а сам отрезок АВ перпендикулярен оси симметрии.
Таким образом, симметричные точки расположены на прямой, перпендикулярной оси симметрии, на равном расстоянии от нее. Для проверки равенства отрезков можно использовать циркуль. (6. с. 245)
В процессе выполнения задания на преобразование фигур и на построение симметричных фигур формируется умение работать с циркулем, чертежным угольником и линейкой.
Исходя из опыта работы, можно сделать вывод, что детям очень интересны эти творческие задания. А завершающим этапом при изучении темы «Симметрия» является построение симметричных фигур.
Для построения симметричных фигур выбираются опорные точки (концы отрезков, центры окружностей), строятся симметричные к ним точки, а затем по этим точкам воспроизводятся сами фигуры. Выполняя эти задания, дети должны заметить, что точки, лежащие на оси симметрии, при симметрии переходят сами в себя. (7. с. 43)
Заключение
На основании изученного мною теоретического материала и собственного опыта работы в начальной школе можно сделать вывод, что акцентирование внимания на геометрической линии в системе Л.Г. Петерсон, оправдано, так как способствует раннему формированию у детей правильного восприятия окружающего мира и помогает более полно подготовить детей к изучению геометрии в средней школе. Таким образом, данная линия является перспективной в развитии образования начальной школы.
Изучив литературу по данной теме и применяя данные знания в своей профессиональной деятельности, мне удалось доказать значимость изучения геометрии по системе Л.Г. Петерсон в начальных классах и практическое значение темы «Симметрия. Преобразование фигур» в жизни человека.
Известный немецкий математик Герман Вейль в своей книге «Симметрия» (2. с.11) дал определение симметрии таким образом: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».
Библиография
1. А.В. Белошистая. Методика обучения математики в начальной школе, М., «Владос», 2007.
2. Вейль Г., Симметрия, пер. с англ., М., 1968. – 192 с.: ил.
3. Н.Я. Виленкин, Н.К. Голубева. Москва 1 – 2 классы, — М; 1979, 1981 г.г.
4. Конспект лекций по системе «Школа 2000» Романовской О.К.
5. Петерсон Л.Г. Математика, 3 класс. Методические рекомендации для учителей. – изд. 3-е, перераб. и доп./Л.Г. Петерсон. – М.: Издательство «Ювента»; 2009. – 336 с.: ил.
6. Петерсон Л.Г. Математика, 2 класс. Методические рекомендации. Пособие для учителей. – М.: «Баласс», «С-инфо»; 1997, — с. 256. ил.
7. Петерсон Л.Г. Математика. 3 класс. Часть 2./Л.Г. Петерсон. – М.: Издательство «Ювента», 2010. – с. 96.: ил.
8. Федеральный компонент Государственного стандарта общего образования. Часть I. Начальное общее образование. Основное общее образование./ Министерство образования РФ. – М. 2004, — с 224
9. «Школа 2000». Математика для каждого: Технология. Дидактика. Мониторинг. Вып. – 4. – М.: УМЦ «Школа 2000 …», 2002.
10. Шубников А.В., Симметрия. (Законы симметрии и их применение в науке, технике и прикладном искусстве), М. – Л., 1940
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых”
(ВлГУ)
кафедра психологии и педагогики дошкольного и начального образования
Реферат на тему
«Преобразование плоскости. Метод изучения симметрии в начальной школе».
Выполнила студентка
гр. ЗНОу-218
Носкова Полина Сергеевна
Руководитель:
ст. преподаватель каф.ППДНО
Болотова Татьяна Владимировна
Владимир 2021 г.
Содержание
Введение……………………………………………………………………….….3
I. Преобразование плоскости………………………………………………….5
II. Метод изучения симметрии в начальной школе……….……………………
III. Вывод……………………………………………………………………….…
IV. Список литературы…………………………………………………………………….…
Введение
В школу ребёнок приходит уже с определёнными знаниями о геометрических фигурах, объектах, среди которых есть и симметричные.
Школа должна ему обеспечить развитие познавательных, интеллектуальных и творческих способностей. Дать учащимся начальные геометрические представления, развить логическое мышление и пространственное воображение детей, сформировать умения узнавать геометрические фигуры и их части.
В курсе начальной школы, главным является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки. Задания на вычисления различных параметров геометрических фигур (длин отрезков, периметра и площади прямоугольника и квадрата).
Неоценимую роль играет изучение алгебраических, геометрических понятий, в том числе и понятия о симметрии. Включение в начальный курс математики темы «Симметрия», использование проектных технологий на уроках и во внеурочное время по формированию понятий о симметрии позволит развить у детей пространственное мышление, расширить знания о геометрических фигурах, подготовить детей к активному и осмысленному восприятию курса геометрии в средней школе. Детям свойственно в этом возрасте усваивать понятия с помощью наглядно-практических методов, игровых, проектных.
Эта работа способствует 3 формированию опыта саморазвития и личностной ответственности учащихся, способности к творческой созидательной деятельности. А это и есть те ключевые компетенции, которые определяют современное качество образования России. На основании вышеизложенного можно сделать вывод, что данная тема, у младших школьников является актуальной, а использование для этого проектных технологий соответствует современным требованиям образования.
Данная тема рассматривает следующую цель:
развитие логического мышления и пространственного воображения детей; формирование умения знать и называть геометрические фигуры, изображать.
На основании цели поставлены задачи:
o развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать
o формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки
I. Преобразование плоскости. Метод изучения симметрии в начальной школе
В программе начальной школы геометрический материал изучается на протяжении каждого года. Особой темы не выделяется, материал изучается не углубленно, только в качестве знакомства без терминологии.
Ученики учатся строить геометрические фигуры, сравнивать их и изображать.
Данную тему мы видим в линии учебников УМК «Школа России», «Перспектива», (Дорофеев Г.В, Миракова Т.Н.), Петерсон и др.
Современные методические подходы, к изучению геометрического материала отражают изменения, которые произошли в начальной школе и обучении математике.
Плоскостные фигуры моделируют форму частей поверхности твердого тела, форму сечений и теней (проекций), алинейные фигуры — форму границ этих поверхностей, сечений и теней. Форму твердого тела можно задать так же определенным расположением точек, «точечной фигурой». Для графического представления формы разработаны специальные правила изображений, правила построения геометрических фигур с использованием определенных наборов чертежных и измерительных инструментов.
Для описания границ поверхностей и границ видимости предназначены линии — замкнутые и незамкнутые, прямые и кривые. Соответствующие геометрические фигуры назовем линейными. Обобщением линий служат понятие прямая и кривая. К линейным геометрическим фигурам относятся также: луч, отрезок, ломаная, многоугольники, понимаемые как замкнутые ломаные линии; угол (как два луча, исходящие из одной точки).
Важную информацию о форме предмета несет форма теней (проекций), форма срезов, сечений тел плоскостью. Наблюдения за тенями (проекциями), срезами способствуют развитию представлений о форме, развитию пространственного воображения и формированию понятий о геометрических фигурах.
Всем известно, как любят дети рисовать. Карандаши, ручки, фломастеры, мелки — любимые «инструменты» детей. Из-под их «пера» выходят линии самой разной формы. Комментируя рисунки, обучая рисованию, взрослые называют формы линий, их расположение относительно друг друга геометрическими терминами. Занятия изобразительной деятельностью оказывают значительное влияние на геометрическое развитие детей.
Плоскостные геометрические фигуры и линии используются в психологических тестах при исследовании мышления. Объясняется это тем, что они удобны для сравнения, образования рядов, представляющих закономерности. С помощью геометрических объектов развивают внимание, память. Модели геометрических фигур, их изображения служат счетным материалом, элементами множеств, с помощью которых представляют числа, арифметические действия, отношения между ними. Геометрические фигуры характеризуются величинами, как и моделируемые ими материальные тела. Все геометрические фигуры, кроме точки, обладают ненулевой длиной. Плоскостные фигуры двумерны, объемные фигуры — трехмерны. Плоскостные и объемные фигуры характеризуются площадью, объемные — объемом. Изучение геометрических величин — важнейший источник представлений учащихся о величинах реальных физических тел.
Симметрия по программе «Школа России» М.И. Моро и др. (Слайд 2)
В программе по математике «Школа России» М.И. Моро и др. прописано, что:
Математические знания и представления о числах, величинах,
геометрических фигурах лежат в основе формирования общей картины мира и познания законов его развития. Именно эти знания и представления необходимы для целостного восприятия объектов и явлений природы, многочисленных памятников культуры, сокровищ искусства.
Обучение младших школьников математике на основе данной программы способствует развитию и совершенствованию основных познавательных процессов (включая воображение и мышление, память и речь).
Содержание курса имеет концентрическое строение, отражающее последовательное расширение области чисел. Такая структура позволяет соблюдать необходимую постепенность в нарастании сложности учебного материала, создаёт хорошие условия для углубления формируемых знаний, отработки умений и навыков, для увеличения степени самостоятельности (при освоении новых знаний, проведении обобщений, формулировании выводов), для постоянного совершенствования универсальных учебных действий.
Структура содержания определяет такую последовательность изучения учебного материала, которая обеспечивает не только формирование осознанных и прочных, во многих случаях доведённых до автоматизма навыков вычислений, но и доступное для младших школьников обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, осознание связей между рассматриваемыми явлениями. Сближенное во времени изучение связанных между собой понятий, действий, задач даёт возможность сопоставлять, сравнивать, противопоставлять их в учебном процессе, выявлять сходства и различия в рассматриваемых фактах.
В связи с концентрическим строение курса тема «Симметрия » изучается на протяжении всех 4 лет обучения.
В 1 классе даются задания на нахождение зеркального отражения фигуры. (слайд 3)
ММ1Ч2с59
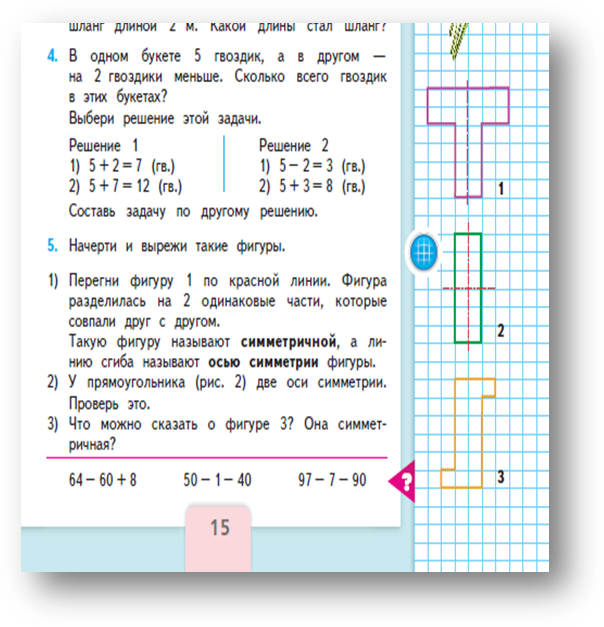
Во втором классе дается определение симметрии и ось симметрии. Так же дети учатся определять оси симметрии. На данную тему так же даются задания. Слайд 4
ММ2Ч1с.15
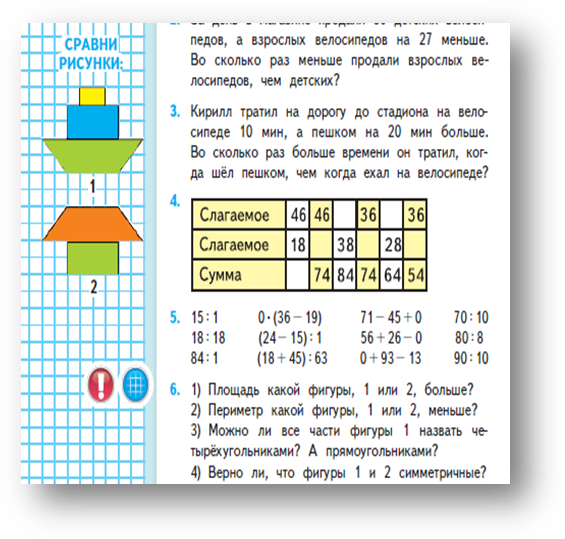
В третьем и четвертом классе акцент на данной теме не делается, но задания на повторения предлагаются. Слайды 5-6
ММ3Ч1с.84
ММ4Ч1с.31
1.2 Симметрия по программе Л.Г. Петерсон Слайд 7
В курсе математики Л.Г. Петерсон сохраняется преемственность с традиционной программой по математике, но усиливается геометрическое содержание за счет большого дополнительного материала (особенно в 4-ом классе), что позволяет расширить геометрические представления и знания учащихся, развивать их пространственное воображение, техническое и логическое мышление, конструкторские умения.
Определяется конкретное содержание, основными положениями которого являются:
• преемственность с традиционным построением курса математики, что обеспечивает числовую грамотность учащихся, умение решать текстовые задачи, знакомство с величинами и их измерением;
• усиление геометрического содержания обеспечивает расширение геометрических представлений и знаний учащихся, развивает их пространственное воображение и логическое мышление. В программу входит знакомство с основными линейными, плоскостными и пространственными геометрическими фигурами и их свойствами. Расширение геометрических представлений и знаний используется для формирования у учащихся элементов технического мышления и конструкторских умений;
• обеспечивается формирование умений изображать на бумаге в форме чертежа сначала элементарных геометрических фигур, а затем конструируемые объекты или их части;
• активизируется творческое мышление, побуждает к поиску нестандартных математических задач.
Изложение геометрического материала проводится в наглядно-практическом плане. Работая с геометрическим материалом, дети знакомятся и используют основные свойства изучаемых геометрических фигур. Задания располагаются в порядке усложнения и постепенного обогащения новыми элементами конструкторского характера.
Уже в 1 классе начальной школы идет пропедевтическая работа по теме «Симметрия», но без введения данного термина. В подготовительной работе по теме предлагаются задания вида: дорисуй по образцу
Особенностью изучения геометрических понятий в программе Л.Г. Петерсон – их раннее введение на основе построенной многоуровневой системы математических понятий. Тема «Преобразование фигур. Симметрия.» в данной программе изучается в 3 классе и ей отводится 4 урока (Уроки 14-17 в соответствии с программой), что соответствует 4 академическим часам. Согласно данной темы программа предусматривает следующие задачи:
— сформировать навык построения симметричных точек, отрезков на клетчатой бумаге с помощью специальных инструментов (линейки, угольника, циркуля);
— уметь строить фигуры, симметричные относительно прямой;
— учить находить и строить линию симметрии в симметричных фигурах.
Реализация задач достигается следующим содержанием программы:
— симметрия (построение симметричных фигур);
— симметричные фигуры (симметрия на клетчатой бумаге).
В заданиях, предложенных Л.Г. Петерсон, предусмотрено использование наглядно-практических и объяснительно-иллюстративных методов и приемов. Слайд 8
На уроках учащиеся выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представление о преобразовании фигур уточняются. Понятие «преобразование фигур» можно пояснить, как перемещение фигур на плоскости, их перенос. На 14 уроке рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево (параллельный перенос) приложение. С детьми надо проговорить вывод о том, что при таких преобразованиях каждая точка фигур перемещается в одном и том же направлении на одно и то же расстояние. При этом линии, соединяющие соответствующие точки фигур, параллельны. Направление расстояния, на которое осуществляется перенос, удобно показывать направленным отрезком или вектором. (с. 37. урок 14)
Для построения симметричных фигур выбираются опорные точки (концы отрезков, центры окружностей), строятся симметричные к ним точки, а затем по этим точкам воспроизводятся сами фигуры. Выполняя эти задания, дети должны заметить, что точки, лежащие на оси симметрии, при симметрии переходят сами в себя. (7. с. 43. урок 16) слайды 9-10
На уроках 22 – 25 учащиеся знакомятся с некоторыми преобразованиями фигур на плоскости (параллельный перенос, симметрия), закрепляют приемы письменного умножения и деления многозначного числа на однозначное, отрабатывают навыки устных вычислений, повторяют и закрепляют нумерацию, сложение и вычитание многозначных чисел, решение текстовых задач и уравнений, зависимость между компонентами и результатами арифметических действий, расширяют представление о геометрических фигурах.
С преобразованием фигур на плоскости учащиеся уже встречались раньше при рассмотрении равенства фигур, в задачах на построение симметричных фигур и др. Однако сам термин «преобразование фигур» не вводился. На данных уроках ученики выполняют практические действия с фигурами на клетчатой бумаге, в процессе которых их представления о преобразовании фигур уточняются.
Понятие «преобразование фигур» можно пояснить как перемещение фигур на плоскости, их перенос. На уроке 22 рассматривается перенос фигур на данное число клеток вверх, вниз, направо и налево (параллельный перенос).
Проблема урока связана с «открытием» свойств этого преобразования, которые позволят строить изображения фигур при их параллельном переносе, а именно:
1. Все точки фигур перемещаются в одном и том же направлении на одно и то же расстояние.
Это означает, что для построения параллельного переноса фигуры можно выбрать «опорные точки», перенести каждую из них в заданном направлении на одно и то же расстояние, а затем восстановить фигуру по полученным точкам.
2. В результате переноса фигур они не деформируются, т. е. получаются равные фигуры.
Значит, для построения параллельного переноса фигуры можно переместить по заданному условию одну какую-нибудь точку, а затем, исходя из нее, восстановить и саму данную фигуру.
Таким образом, на этапе актуализации знаний требуется восстановить в памяти обучающихся понятие равных фигур: две фигуры равны, если их можно совместить наложением.
Задание № 1, стр. 37 можно использовать на этапах постановки проблемы и «открытия» нового знания. В этом задании в результате выявленных свойств учащиеся переносят данную фигуру сначала на 7 клеток вправо, а затем на 3 клетки вниз одним из указанных выше способов.
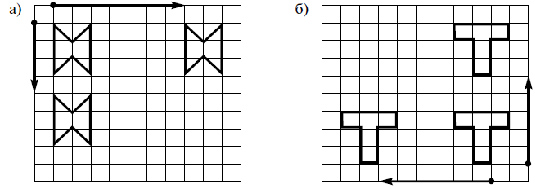
Задания № 2–4, стр. 37 предназначены для этапа первичного закрепления. В № 2 ученики должны выразить в речи выполняемые преобразования. Можно сказать им, что направление и расстояние, на которое осуществляется перенос, удобно показывать направленным отрезком (вектором), и попросить нарисовать направленные отрезки, соответствующие данным преобразованиям. Так, в задании (а) горизонтальный вектор означает, что фигура переносится на 7 клеток вправо, а вертикальный – что она переносится на 4 клетки вниз; в задании (б) горизонтальный вектор показывает, что фигура переносится на 6 клеток влево, а вертикальный – что она переносится на 5 клеток вверх: Слайд 11
В задании № 3, стр. 37 учащиеся должны не просто выполнить преобразования, но и найти результат их последовательного выполнения (композиции): два переноса – сначала на 15 клеток вправо, а потом на 3 клетки влево – можно заменить одним переносом на 12 клеток вправо. В задании № 4, стр. 37 учащиеся встречаются с понятием обратного преобразования.
Задание № 5, стр. 37 можно использовать на этапе самостоятельной работы с самопроверкой в классе. Учащиеся строят в тетради произвольный треугольник, переносят его сначала на 6 клеток вправо, потом на 8 клеток вниз и, наконец, на 6 клеток влево. В завершение они устанавливают, что все эти преобразования можно было заменить одним – переносом треугольника на 8 клеток вниз.
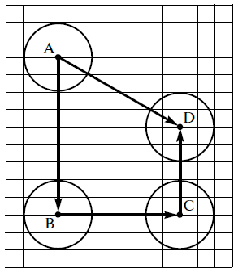
Наиболее трудное задание № 6, стр. 38. Предыдущие выполнялись с помощью линейки, а для выполнения этого задания нужен циркуль. Ученики вспоминают, как надо чертить окружность с помощью циркуля, а потом переносят круг, ограниченный этой окружностью, сначала на 9 клеток вниз, потом на 7 клеток вправо, а потом на 5 клеток вверх. Обучающихся надо подвести к мысли о том, что все эти преобразования можно заменить одним преобразованием, определяемым направленным отрезком (или вектором) AD. Слайд 12
В отличие от традиционной программы, эта тема является дополнительной линией по системе Л.Г. Петерсон.