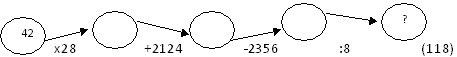- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Понятие о натуральном числе
Натуральные числа и десятичная запись числа
Чтобы сосчитать некоторое количество предметов, используются числа, которые называют натуральными.
С помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно записать любое натуральное число. (подобным образом мы используем буквы алфавита, чтобы записать слова)
Такую запись числа называют десятичной ‒ десять единиц каждого разряда составляют одну единицу следующего старшего разряда.
Натуральный ряд
Если натуральные числа записать в порядке возрастания, то получится ряд натуральных чисел ‒ натуральный ряд.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
Каждое число в этом ряду меньше последующего на единицу. Наименьшее число среди натуральных чисел — это 1, а наибольшего числа нет.
Многозначные числа
Натуральное число называют однозначным, если его запись состоит из одного знака — одной цифры.
Например, числа 3, 7, 9 — однозначные.
Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.
Например, числа 25, 44, 65, 80 — двузначные.
Числа 100, 543, 888 — трёхзначные:
Числа 2000, 6791, 1060 — четырёхзначные и т. д.
Двузначные, трехзначные, четырёхзначные, пятизначные и т. д. — это многозначные числа.
Классы и разряды
Прочитать записи однозначных, двузначных и трехзначных чисел (например: 7, 54, 976) затруднений не вызывает.
Чтобы прочесть многозначное натуральное число, его необходимо разбить справа налево на группы по три цифры в каждой. Крайняя левая группа может состоять из одной или двух цифр.
Эти группы называют классами.
Три первые цифры справа ‒ это класс единиц, три следующие — класс тысяч, затем класс миллионов, класс миллиардов и т. д.
Место, занимаемое цифрой в записи числа, называют разрядом.
Если считать справа налево, то первое место в записи числа называют разрядом единиц, второе — разрядом десятков, третье — разрядом сотен и т. д.
Например, в числе 5034 имеем 4 единицы разряда единиц, 3 единицы разряда десятков, 0 единиц разряда сотен и 5 единиц разряда тысяч.
Можно также сказать, что в классе единиц 34 единицы.
Названия некоторых больших чисел
1 тысяча (1 тыс.) – 1 000 (тысяча)
1 миллион (1 млн) – 1 000 000 (тысяча тысяч)
1 миллиард (1 млрд) – 1 000 000 000 (тысяча миллионов)
1 триллион (1 трлн) – 1 000 000 000 000 (тысяча миллиардов)
Рассмотрим число 6 000 126 754.
Его читают: 6 миллиардов 126 тысяч семьсот пятьдесят четыре.
В классе миллионов во всех разрядах стоят нули. Поэтому при чтении числа 6 000 126 754 не произносят название этого класса.
Примеры прочтения чисел:
а) Число 200 700 читается так: двести тысяч семьсот;
б) Число 6 000 008 читается так: шесть миллионов восемь;
в) Число 14 000 002 000 читается так: четырнадцать миллиардов две тысячи.
Значение цифры в записи числа
Значение цифры зависит от её позиции (места) в записи числа.
Например, в записи числа 56 978 цифра 8 означает 8 единиц, так как она стоит на последнем месте в записи числа (в разряде единиц);
В записи числа 42 389 цифра 8 означает 8 десятков, так как она стоит на предпоследнем месте в записи числа (в разряде десятков);
В записи числа 5 300 847 цифра 8 означает 8 сотен, так как она стоит на третьем месте от конца в записи числа (в разряде сотен).
Число 0 и цифра 0
Число 0 натуральным не является.
Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль» (что означает ‒ «ни одного»).
(Например, счёт 1 : 0 хоккейного матча говорит о том, что вторая команда не забила ни одной шайбы в ворота противника.)
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 12,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 530,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 538,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 557,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1331,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1345,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 957,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 22,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 127,
Мерзляк, Полонский, Якир, Учебник
Номер 133,
Мерзляк, Полонский, Якир, Учебник
Номер 164,
Мерзляк, Полонский, Якир, Учебник
Номер 334,
Мерзляк, Полонский, Якир, Учебник
Номер 588,
Мерзляк, Полонский, Якир, Учебник
Номер 912,
Мерзляк, Полонский, Якир, Учебник
Задание 127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 413,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 214,
Мерзляк, Полонский, Якир, Учебник
Номер 241,
Мерзляк, Полонский, Якир, Учебник
Номер 247,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 394,
Мерзляк, Полонский, Якир, Учебник
Номер 423,
Мерзляк, Полонский, Якир, Учебник
Номер 488,
Мерзляк, Полонский, Якир, Учебник
Номер 489,
Мерзляк, Полонский, Якир, Учебник
Номер 492,
Мерзляк, Полонский, Якир, Учебник
Номер 496,
Мерзляк, Полонский, Якир, Учебник
Содержание:
- Введение
- Происхождение номеров
- Происхождение счета в древности
- История происхождения натуральных чисел
- За основу арифметики. Натуральная числовая линия
- Натуральные числа, основные функции натуральных чисел
- Характеристика количества объектов
- История возникновения нуля
- Индия
- Заключение
- Список литературы
| Тип работы: | Реферат |
| Дата добавления: | 21.01.2020 |
- Данный тип работы не является научным трудом, не является готовой выпускной квалификационной работой!
- Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
Если вы хотите научиться сами правильно выполнять и писать рефераты по любым предметам, то на странице «что такое реферат и как его сделать» я подробно написала.
Введение
Номер — одно из фундаментальных понятий математики. Концепция числа, разработанная в тесной связи с изучением магнитуд, продолжается и по сей день. Во всех областях современной математики необходимо учитывать различные количества и работать с числами. Современный человек постоянно сталкивается в своей повседневной жизни с числами и цифрами. Что означает слово «число»? Первоначально понятия абстрактного числа не существовало, число было «привязано» к подсчитываемым объектам.
С развитием письма появляется абстрактное понятие натурального числа. Первое научное определение числа было дано Евклидом в его «Элементах», которые он взял у своего соотечественника Евдокса Младенца: «Единицей является то, согласно которому каждая из соответствующих вещей называется единицей». Число — это количество, состоящее из единиц». Математик Магнитский так же определил число в своей «Арифметике» (1703). Еще до Евклида Аристотель дал следующее определение: «Число — это количество, измеренное единицами».
В своей «Всеобщей арифметике» (1707) Исаак Ньютон писал: «Под числом мы понимаем не столько количество единиц, сколько абстрактное соотношение одного количества к другому количеству того же рода, взятому в качестве единицы. Целое число — это то, что измеряется одной единицей…». В настоящее время математик С.Ф. Клюйков также внес свой вклад в определение числа: «Числа — это математические модели реального мира, придуманные человеком для своих знаний».
Считается, что термин «натуральное число» впервые использовался римским государственным деятелем, философом и автором математики и теории музыки Бетием (480-524), однако греческий математик Никомах из Геразы говорил о натуральном, т.е. естественном ряду чисел. Термин «натуральное число» в его современном понимании использовался последовательно французским математиком Далембером (1717-1783).
Вопрос об обосновании концепции натуральных чисел долгое время не поднимался в науке. Понятие натурального числа настолько знакомо и просто, что нет необходимости определять его в терминах простых понятий. В процессе работы над аннотацией появляется возможность больше узнать об истории возникновения числа, а также о понятии натурального числа.
Происхождение номеров
Происхождение счета в древности
Наши первые представления о количестве и форме пришли из очень далекой эпохи палеолита. До перехода от простого сбора продуктов питания к активному производству продуктов питания, от охоты и рыбной ловли к сельскому хозяйству люди не добились большого прогресса в понимании количественных показателей и пространственных отношений.
Самым трудным этапом, через который прошло человечество в разработке понятия числа, считается присвоение единицы из понятия «многие». Скорее всего, это произошло в то время, когда человечество находилось на более низкой стадии развития. В.В. Бобынин объясняет такое задание тем, что, как правило, человек рукой хватает предмет, а это, по его мнению, отличает единицу от толпы. Таким образом, Бобынин думает о начале нумерации как о создании системы, состоящей из двух представлений: единицы и неопределенной величины.
Например, племя Ботокуд, жившее в Бразилии, выражало числа только словами «один» и «многие». Внешний вид элемента «два» объясняется идентификацией возможности взятия предмета в каждой руке. На ранних стадиях счета люди связывали это понятие с идеей о том, что обе руки держат по одному предмету, «три» определялись путем поднятия обеих рук и указания на ноги. Отсюда и понятие «четыре» также было относительно чеканным, так как оно вызывалось сопоставлением двух рук и двух ног с одной стороны, и умением поставить предмет на каждую ногу с другой.
Дальнейшее развитие счета, вероятно, относится к той эпохе, когда было сформировано первобытное коммунистическое общество с соответствующим распределением пищи, одежды и орудий труда. Эти обстоятельства заставили человека так или иначе вести учет общей собственности, враждебных сил, с которыми ему приходилось соперничать в борьбе за обладание новыми территориями. Процесс подсчета не мог больше останавливаться в четыре и должен был продолжать развиваться.
На этой стадии развития человек уже отказывается от необходимости брать в руки подсчитанные предметы или ставить их у ног. Первая абстракция в математике состоит в замене подсчитанных объектов на некоторые другие схожие объекты или знаки: Камешки, ветки, веточки, выемки. Операция основана на принципе соответствия один к одному: для каждого подсчитываемого объекта добавляется один из объектов, выбранных в качестве счетного средства (т.е. камешек, узел на строке и т.д.).
Следы этого вида счета сохранились среди многих народов и по сей день. Иногда такие примитивные счетные инструменты (камни, ракушки, кости) нанизывали на строку или палку, чтобы не потерять их. Это привело к созданию более совершенных очков, дошедших до наших дней: российских скутеров и аналогичных китайских суан-панов.
История происхождения натуральных чисел
Понятие натурального числа, возникшее из необходимости считать предметы, имело свое происхождение в доисторические времена. Процесс формирования понятия натурального числа заключался в следующем. На самом низком уровне первобытного общества понятие абстрактного числа отсутствовало. Это не означает, что первобытный человек не мог знать количество объектов определенного количества, например, количество людей, участвующих в охоте, количество озер, в которых можно ловить рыбу и т.д.
Но сознание первобытного человека еще не сформировало того общего, что есть в объектах такого рода, таких как «три человека», «три озера» и т. д. Анализ языков первобытных народов показывает, что словесные выражения использовались для подсчета объектов различного рода. Слово «три» в контексте «три человека», «три лодки» было сделано по-другому. Конечно, такие именованные серии чисел были очень короткими и заканчивались индивидуализированным понятием («множество») большого количества тех или иных объектов, которое также называлось, то есть выражалось разными словами для объектов разного рода, таких как «толпа», «стадо», «куча» и т.д.
Истоком понятия абстрактного числа является примитивный подсчет объектов, который заключается в сравнении объектов данного конкретного множества с объектами данного конкретного множества, играющими, как бы, роль части стандарта.
Среди большинства народов первыми такими эталонами являются пальцы (палец подсчитывается, о чем говорилось выше), что, несомненно, подтверждается лингвистическим анализом названий первых чисел. На этом этапе число становится безошибочным, оно не зависит от качества подсчитываемых объектов, а появляется одновременно в весьма конкретной реализации, связанной с природой эталонной совокупности. Растущая потребность в подсчете вынудила людей использовать другие стандарты подсчета, такие как надсечки на палочке. Для фиксации относительно больших чисел появилась новая идея маркировки определенного числа (десять для большинства народов) новым знаком, например, выемкой на палочке.
С развитием письменности возможности воспроизведения чисел значительно расширились. Сначала цифры стали обозначаться строками на материале, используемом для записи (папирус, глиняные таблетки и т.д.). Затем были введены другие знаки для больших чисел. Вавилонские клинописные цифры, как и дошедшие до нас «римские цифры», ясно свидетельствуют именно о таком способе формирования нотации для числа.
Шагом вперед стала индийская система позиционного письма, позволяющая записывать любое натуральное число десятью символами — цифрами. Таким образом, параллельно с развитием письменности устанавливается понятие натурального числа в виде слов (в устном языке) и в виде обозначения специальными знаками (в письменной форме).
Важным шагом в развитии концепции натурального числа является признание бесконечности натурального ряда чисел, т.е. потенциальной возможности его бесконечного продолжения.
Вопрос об обосновании понятия естественного числа уже давно перестал возникать в науке. Понятие натурального числа настолько знакомо, что нет необходимости определять его в терминах более простых понятий. Только в середине 19 века, под влиянием развития аксиоматического метода в математике, с одной стороны, и критического пересмотра основ математического анализа, с другой, стала очевидной необходимость установления понятия количественного натурального числа.
Явное определение понятия натурального числа, основанное на понятии количества (набора объектов), было дано в 70-х годах 19 века в сочинениях Г. Кантора:
- Во-первых, он определяет понятие равенства множеств. А именно, два набора называются эквипартитами, если объекты, из которых они состоят, можно сравнить по отдельности. Затем определяется число объектов, составляющих данную совокупность, как то, что эта совокупность и любая другая совокупность объектов, равная ей, имеют общие, независимо от качественных характеристик этих объектов. Это определение отражает сущность натурального числа в результате подсчета объектов, составляющих заданное множество.
Цифры возникли из необходимости считать и измерять и прошли долгий путь исторического развития.
Было время, когда люди не умели считать. Для сравнения конечных множеств они устанавливали соответствие один к одному между заданными множествами или между одним из множеств и подмножеством другого множества, т.е. на данном этапе люди воспринимали количество элементов без пересчета. Например, о количестве множества из двух объектов он мог сказать: «столько же, сколько рук человека», о множестве из пяти объектов — «столько же пальцев на руке». Таким образом, сравниваемые наборы должны были быть одновременно наблюдаемыми.
В результате очень долгого периода развития человек подошел к следующему этапу генерации натуральных чисел — для сравнения количеств он стал использовать количественные посредники: мелкие камни, ракушки, пальцы. Эти количественные посредники уже представляли зачатки понятия натурального числа, хотя даже на этом этапе число не отделялось от подсчитываемых объектов: например, речь шла о пяти камешках, пяти пальцах, но не о «пяти» в целом.
Для определения количества сравниваемых с ними количественных показателей стали использоваться названия количественных показателей. Так, среди некоторых племен число множества, состоящего из пяти элементов, называлось словом «рука», а число множества, состоящего из 20 элементов, называлось словом «все люди».
Только тогда, когда человек научился оперировать количествами, установил общность, существующую, например, между пятью пальцами и пятью яблоками, то есть, когда абстрагировался от природы элементов количеств, возникла идея естественного числа. На этом этапе, например, при подсчете яблок, слова «одно», «два яблока» и т.д. больше не перечислялись, а произносились слова «одно», «два» и т.д. Это был важнейший этап в развитии концепции числа.
Историки полагают, что это произошло в каменном веке, в эпоху первобытно-общинного строя, примерно в 10-5 тысячелетии до нашей эры.
Появление концепции натурального числа стало важнейшим моментом в развитии математики. Исследование этих чисел стало возможным независимо от конкретных задач, в связи с которыми они возникли. С развитием концепции натурального числа в результате подсчета объектов при использовании действий над числом.
Операции сложения и вычитания впервые появились как операции над самими агрегатами в виде объединения двух агрегатов в один и разделения части агрегата. Умножение возникло, по-видимому, в результате подсчета на равные части (на две, на три…), деление — как разделение населения на равные части.
Только в многовековом опыте сформировалось представление об абстрактном характере этих действий, о независимости количественного результата действия от природы субъектов, образующих агрегат, о том, что, например, два субъекта и три субъекта образуют пять субъектов, независимо от природы этих субъектов. Затем они начали разрабатывать правила действий, изучать их свойства, создавать методы решения проблем, то есть началось развитие науки о числе.
Теоретическая наука, которая начала изучать числа и действия, связанные с ними, называлась «арифметикой». Слово «арифметика» происходит от греческого arithmos, что означает «число». Следовательно, арифметика — это наука о числах.
Термин «натуральное число» был впервые использован в V веке римским ученым А. Бетием, известным как переводчик трудов известных математиков прошлого на латинский язык и автор книги «О введении в арифметику», которая стала образцом для всей европейской математики вплоть до XVI века.
Во второй половине XIX века выяснилось, что натуральные числа являются основой всей математической науки, и от их состояния зависит сила всего математического строя. В связи с этим возникла необходимость строго логически обосновать понятие натурального числа, систематизировать то, что с ним связано.
Когда математика XIX века перешла к аксиоматическому построению своих теорий, была разработана аксиоматическая теория натурального числа. Теория множеств, возникшая в XIX веке, также оказала большое влияние на изучение природы натурального числа. Конечно, в возникших теориях понятия естественного числа и действия о них стали более абстрактными, но это всегда связано с процессом обобщения и систематизации отдельных фактов.
Дальнейшее расширение понятия числа больше не обусловлено насущными потребностями в подсчете и измерении, а является следствием развития математики.
За основу арифметики. Натуральная числовая линия
Как мы уже говорили, арифметика — это наука, которая имеет дело с числами и операциями над ними. Подсчет — основа арифметики.
Прежде чем научиться арифметике, необходимо научиться считать и уметь писать числа. Для подсчета используются названия чисел и специальные знаки для их краткого представления. Символы, используемые для представления чисел, называются цифрами. Почти везде в мире десять цифр (от 0 до 9) служат алфавитом на языке чисел; эти цифры называются арабскими цифрами. Девять из них используются для обозначения первых девяти натуральных чисел, а нулевое число, представленное цифрой 0, используется для обозначения отсутствия объектов.
Все числа: 1, 2, 3, 4,…17,18 и т.д., без конца называются натуральными, а сами числа называются натуральными числами. В строке с натуральным номером любое число, начинающееся с 2, на одно больше, чем предыдущее. Натуральные числа формируются путем подсчета объектов и значений измерений. Но если в результате измерения получаются числа, отличные от натуральных, то подсчет только натуральных чисел. Для того, чтобы отсчитывать, нам нужна последовательность чисел, которая начинается с одной и позволяет переходить от одной цифры к другой столько раз, сколько необходимо.
Другими словами, нам нужен сегмент натуральной последовательности чисел. Поэтому для того, чтобы решить проблему обоснования системы натуральных чисел, сначала необходимо было ответить на вопрос, что же такое число как элемент последовательности натуральных чисел. Ответ на этот вопрос был дан в работах двух математиков — немецкого Грассмана и итальянского Пеано. Они предложили аксиоматику, при которой натуральное число оправдывается как элемент бесконечно непрерывной последовательности.
Важным шагом в развитии концепции натурального числа является понимание бесконечности натуральной последовательности чисел, то есть потенциальной возможности ее бесконечного продолжения.
Человечеству потребовалось много времени, чтобы перейти к 1-ой стадии численного обобщения. Для создания кратчайших серий натуральных чисел от одного до бесконечности потребовалось сто столетий. Натуральные числа, потому что они обозначают (моделируют) реальные неделимые объекты: людей, вещи, животных.
Натуральные числа, основные функции натуральных чисел
Натуральные числа — это целые числа. Ноль также относится к целым числам, но не является одним из натуральных чисел. Не следует путать термины «числа» и «цифры». Вы можете писать столько цифр, сколько захотите, но есть только десять цифр. Мы пишем каждое натуральное число этими десятью цифрами. При подсчете объектов в качестве маркера ордера мы используем натуральный номер. В задачах, связанных с измерением количеств, число действует как значение количества с выбранной единицей, т.е. как мера количества. Большое внимание уделяется и другой роли числа — как составной части вычислений. Таким образом, натуральное число имеет множество функций.
Характеристика количества объектов
Характеристика порядка расположения объектов в серии.
В соответствии с этими функциями возникли понятия порядкового номера (первый, второй и т.д.) и количественного номера (один, два и т.д.). В частности, расположение в ряду подсчитываемых объектов и их последующий пересчет с использованием порядковых номеров всегда был наиболее распространенным методом подсчета объектов (таким образом, если последний из подсчитываемых объектов оказывается седьмым, это означает, что их насчитывается семь).
История возникновения нуля
Ноль (от латинского Nullus — нет) — это имя первого (по порядку) числа в стандартных системах счисления, а также математический знак, выражающий отсутствие значения этой категории в числе, заданном в системе позиционной нотации. Ноль, помещенный справа от другого числа, увеличивает значение левой цифры на одну (соответственно, умножается на десять в десятичной системе счисления).
Индия
Основным преимуществом внедрения методов записи чисел индейцами является то, что они значительно сократили количество цифр, применили позиционную систему десятичного счета, а также ввели нулевой знак. Введение нуля, цифр и принципа их локальной значимости облегчило арифметические операции над числами и, следовательно, арифметический расчет и претерпело значительное развитие в Индии.
Индейцы называли знак, указывающий на отсутствие цифры в числе словом «сунья», что означает «пустота» (цифра, место). Арабы перевели это слово по смыслу и получили слово «сифр», от которого происходит слово «цифра». Харьязми первым использовал в своих рассказах число «ноль». Первая достоверная запись о написании нуля датируется 876 г., в настенной надписи из Гвалиора (Индия) найдено число 270.
Некоторые исследователи полагают, что ноль был заимствован у греков, которые использовали букву «о» в качестве нуля в шестнадцатеричной системе счисления, которую они использовали в астрономии. Другие же считают, что ноль пришел в Индию с Востока; он был изобретен на границе между индийской и китайской культурами. Более ранние надписи, датированные 683 и 686 годами, были обнаружены на территории нынешней Камбоджи в Индонезии, где ноль представлен в виде точки и небольшого круга. Сначала индейцы представляли ноль как точку. Когда в V веке н.э. индейцы ввели нулевой знак, они смогли отказаться от позиционной системы счисления и разработать абсолютную позиционную десятичную систему, превосходство которой в подсчете, хотя и не признано, повседневно используется сотнями миллионов людей.
Математическое число ноль конечно.
Заключение
На первых этапах развития понятие числа определялось потребностями в подсчете и измерении, которые возникали в непосредственной практической деятельности человека. Тогда число становится основным понятием математики, и дальнейшее развитие понятия числа определяется потребностями этой науки. Мир полон тайн и загадок. Современная наука встречается с ценностями настолько сложного характера, что для их изучения приходится изобретать все новые типы чисел.
Рассмотрев этот вопрос, можно с уверенностью сказать, что историческая информация изменчива, и со временем, возможно, мы узнаем много нового о том, что, кажется, уже известно, и что-то не менее интересное и неисследованное в настоящее время также будет обнаружено.
Список литературы
- Задачник-практикум по математике. Пособие для студентов-заочников факультетов подготовки учителей начальных классов пединститутов под ред. Н.Я. Виленкина. Москва «Просвещение», 1978.
- Марков С.Н. Курс истории математики: Учебное пособие. — Иркутск: Издательство иркутского университета, 1996.
- Стойлова Л.П., Виленкин Н.Я., Лаврова Н.Н. Математика. В 2ч. Ч1. Для студентов — заочников 1-2 курсов фак. подгот. учителей нач. классов пед. ин-тов; Моск. Гос. Пед. Ин-т. М.: Просвещение, 1991.
В процессе работы над индивидуальным исследовательским проектом по математике на тему «Натуральные числа» автором была поставлена цель, выяснить, как сформировалось у людей первое представление о натуральных числах и как оно изменялось с развитием науки математики, дается обоснование определениям «натуральные числа» и «системы счисления».
Подробнее о работе:
В ученическом проекте по математике «Натуральные числа» автором была изучена теория о появлении натуральных чисел, их роли в науке и обыденной жизни, рассматривает существующие системы счисления и возможные математические действия над натуральными числами, характеризует простые и составные числа.
Учебная исследовательская работа по математике на тему «Натуральные числа» подробно описывает свойства сложения и вычитания, умножения и деления натуральных чисел, описывает занимательные факты о натуральных числах. В исследовательской работе автор приводит решение задач и примеров с натуральными числами на каждое математическое действие и выдвинутые гипотезы.
Оглавление
Введение
1. Натуральные числа.
1.1. Причины возникновения натуральных чисел.
1.2. Системы счисления.
2. Действия над натуральными числами и их свойства.
2.1. Свойства сложения и вычитания.
2.2. Умножение натуральных чисел и его свойства.
2.3. Делимость натуральных чисел и его свойства.
2.4. Простые и составные числа.
3. Занимательные факты о натуральных числах.
Заключение
Список использованной литературы
Введение
Для счета предметов используются числа 1,2,3,4,5 и т.д. Такие числа подходят для подсчета яблок в вазе, грузовиков в гараже, учебников в классе. Кроме того, они используются для измерения величин: длины, площади, массы, времени, скорости. Но числа появляются не только тогда, когда мы считаем предметы или единицы измерения. Подсчитывать приходиться и многое другое: количество рейсов самолетов между городами, уроков математики в учебном году, глав в книге и т.д.
Для таких чисел используют специальное название – натуральные числа.
В рамках школьной программы история математики изучается поверхностно. Мы мало знаем о происхождении тех или иных терминах и математических понятиях. Понятие натуральных чисел не имеет чёткого и безупречного определения, но математики долгое время опираются на него при определении других важных понятий. Кажется, что человеку всегда приходилось складывать, вычитать, умножать и делить, т.е. числа всегда сопровождали человека по жизни. Но как появились первые натуральные числа, почему они возникли, и какую роль играют в жизни человека?
На эти вопросы я попыталась ответить в своей работе.
Я поставила перед собой цели:
- Выяснить, как сформировалась у людей первое представление о натуральных числах, как оно изменялось с развитием науки математики.
- Изучить необычные и ранее неизвестные факты о натуральных числах.
- Изучить теоретический материал по теме работы.
Для достижения поставленных целей необходимо было решить следующие задачи:
- Ознакомиться с литературой о натуральных числах.
- Обобщить полученные знания в своей работе.
Объект: натуральные числа.
Предмет: математические действия с натуральными числами.
Причины возникновения натуральных чисел
Натуральные числа – это первая числовая система, с которой встречается человек в своей жизни. Простейший вид чисел — натуральные числа — исторически возник из потребностей счета: одна лодка, два человека, три дерева и т.д.
Лишь на достаточно высоком интеллектуальном уровне было осознано, что у конкретных предметных групп «два камня», «две птицы» и «две руки» есть нечто общее: «два». Абстрактные, отвлеченные числа позволяли сравнивать количество предметов в разных группах, что имело важное значение при обменных операциях типа «раковина за орех».
Число — важнейшее понятие математики. Потребовалось несколько тысячелетий, чтобы это понятие приобрело тот вид, который в настоящий момент признается удовлетворительным для большинства математиков. Однако в соответствующих формулировках используется профессиональный язык такого высокого уровня, что попытка передать их точный смысл «простыми и понятными словами» безнадежна. Приходится довольствоваться лишь общими описаниями.
Числа 1,2,3,4,5,6,7,8,9, использующиеся для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называют натуральными.
Системы счисления
Развитие счета шло параллельно с изменением в психологическом восприятии понятия «много». Вначале было «один, два, много» или «один, два, три, много», но постепенно граница отодвигалась, формировался натуральный ряд чисел: 1, 2, 3, 4 и т.д.
Пальцы на руках установили первый предел счёта: десять. Принцип группировки по десять позволял охватывать все большие количества предметов, объединяя их в новые единицы счета: десять десятков — сотня, десять сотен — тысяча, дальше десяти тысяч обыденный разум не заглядывал. Так сформировалась десятичная система счисления.
Она позволяла с помощью небольшого количества слов называть все встречающиеся числа: например, триста шестьдесят пять — это три сотни и шесть десятков и пять единиц. Не у всех народов десяток стал основным числом счета: одни осознали в качестве первой границы пять (пальцы одной руки), другие — двадцать (все пальцы на руках и на ногах), в Вавилоне употреблялась система с загадочным основанием шестьдесят, в согласии с ней мы до сих пор делим окружность на триста шестьдесят градусов и измеряем время: в часе — шестьдесят минут, в минуте — шестьдесят секунд. Но в конце концов десятичный принцип стал общепризнанным.
С появлением письменности возникла проблема записи чисел. Древние греки и евреи применяли алфавитную систему нумерации: числа от единицы до девяти, а затем все десятки и сотни обозначались буквами в порядке алфавита, над которыми ставилась черта.
Создатели славянского письма перенесли этот прием на новую почву: знаки кириллицы, соответствовавшие греческим буквам, получили те же числовые значения (но алфавитный порядок при этом нарушился), сверху ставилось титло. Таким образом, приходилось запоминать 27 (проверьте) числовых знаков — цифр.
Числа 1,2,3,4,5,6,7,8,9,0 – эти числа называются арабскими.
В древности числа записывали палочками: II- один, IIIII — пять, IIIIIIIIII- десять и т.п. Но это было неудобно, и люди искали и находились другие, каждый раз все более современные способы записи чисел. В Западной Европе вплоть до XVIII века в официальных документах применялась римская буквенная нумерация.
Числа записывали при помощи букв латинского алфавита: I-1, V-5, X-10, L-50, C-100, D-500, M-1000. Число также записывалось в виде последовательности цифр, но из эстетических соображений запрещалось четырехкратное повторение одной и той же цифры. Так что числа 4, 9, 40, 90, 400, 900 обозначались соответственно как IV, IX, XL, XC, CD, CM,- меньшая по значению цифра оказывалась левее большей (но часовщики упорно писали на циферблатах IIII, чтобы не путать с шестеркой VI).
В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначения дат, в порядковых номеров, значительных событий, годовщины. Примеры: 31.XII, Сонет CCLXIX.
Любое натуральное число в десятичной системе записывают с помощью цифр: 0,1,2,3,4,5,6,7,8,9. Например, запись 2457 означает, что 2-цифра тысяч, 4- цифра сотен, 5- цифра десятков, 7-цифра единиц; то есть 2457 = 2*1000+4*100+5*10+7. Вообще, если, а – цифра единиц, b – цифра сотен, с – цифра десятков, d – цифра единиц, то имеем а*1000+b*100+с*10+d.
Сначала математические операции «обыгрываются» на реальных предметах и тем самым формируют у людей представление о натуральных числах, как о числах, употребляющихся для счёта. Строгое определение натуральных чисел производиться аксиоматически.
В основе любой аксиоматики натуральных чисел лежит, по сути, одно присущее им свойство – «следовать за».
- Единица – натуральное число, которое не следует ни за каким натуральным числом.
- За каждым натуральным числом следует одно и только одно натуральное число.
- Каждое натуральное число, отличное от 1, следует за одним и только одним натуральным числом.
- Совокупность натуральных чисел, содержащая число 1, а вместе с каждым числом и следующее за ним число, содержит все натуральные числа. Множество натуральных чисел обозначается N:N ={1, 2, 3… n:.. }
Множество натуральных чисел имеет наименьший элемент – 1, но неограниченно сверху.
В наше время почти все народы пользуются счётом десятками, сотнями, тысячами, то есть десятичной системой счисления. В ней значение цифры зависит от позиции, которое оно занимает в записи числа. Поэтому такую систему счисления называют позиционной. В тёплых странах Африки и Америки, где люди ходили босыми, для счёта применялись не только пальцы рук, но и пальцы ног.
Получался счёт двадцатками. Позиционная система записи чисел арабскими цифрами получила широкое распространение в Европе со второй половины XV века. Она оказалась значительно удобнее и проще римской нумерации, которая позиционной не является. С помощью позиционной системы легко записываются как малые, так и большие числа.
Значение цифры зависит от её места в записи числа. Например, цифра 6 означает:
- 6 единиц, если она стоит на последнем месте в записи числа (в разряде единиц).
- 6 десятков, если она стоит на предпоследнем месте (в разряде десятков).
- 6 сотен, если она стоит на третьем месте от конца (в разряде сотен).
Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа «нуль». Это число означает, ни одного. Счёт 0:10 волейбольного матча говорит о том, что первая команда не забила ни одного гола в сетку противника. Нуль не относят к натуральным числам.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идут классы миллионов, миллиардов и т. д.
Миллион – это тысяча тысяч (1000 тыс.), его записывают 1 млн или 1 000 000.
Миллиард – это 1000 миллионов. Его записывают 1 млр или 1 000 000 000. Чтобы прочитать число, называют слева по очереди число единиц каждого класса и добавляют название класса. Не произносят название класса единиц, а также класса, все три цифры которого – нули.
Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особым знаком «-» (титло), который писали над буквой. Первые девять букв алфавита обозначали единицы, следующие девять букв – десятки, а последние 9 букв – сотни. Число 10 тысяч называли словами «тьма» (и теперь мы говорим: народу – тьма тьмущая).
Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли у индусов. Поэтому цифры, которыми мы считаем, пользуемся, европейцы называют «арабскими», а арабы – «индейскими». Эта система была введена в Европе примерно в 1120 году английским учёным – путешественником Аделардом.
К 1600 году она была принята в большинстве стран мира. Русские названия чисел тесно связаны с десятичной системой счисления. Например, пятнадцать означает «пять на десять», пятьдесят – «пять десятков», а пятьсот – «пять сотен».
Действия над натуральными числами и их свойства
Свойства сложения и вычитания. Для натуральных чисел определены операции сложения и умножения, причём сумма и произведение являются также натуральными числами. Натуральные числа можно
складывать
. Числа, которые складывают, называются
слагаемыми.
Число, получающееся при сложении этих чисел, называется их суммой. Сложить числа 2+5 – значит прибавить к числу 2 5раз единицу. Получим 2+5=2+1+1+1+1+1=3+1+3=7, короче 2+5=7.
Если м,n – натуральные числа, то р = m+n – тоже натуральное число, м и n – слагаемые, р – сумма, р = mn – тоже натуральное число, м,n – множители, р – произведение.
Справедливы следующие свойства сложения натуральных чисел:
Переместительное свойство – это когда сумма чисел не изменяется при перестановке слагаемых.
Например: 2+8=10, 8+2=10; а+b=b+а.
Сочетательное свойство – это когда нужно прибавить к числу сумму 2х чисел. Надо сначала прибавить I слагаемое, а потом к полученной сумме – второе слагаемое.
Например: 2+(5+3)=2+8=10
(2+5)+3=7+3=10
(а+b)+с=d+(b+с)=(а+с)+b.
Натуральные числа также можно вычитать. Вычитание – это действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое. Число, из которого вычитают называется уменьшаемым, а число, которое вычитают – вычитаемым. Результат вычитания называют разностью.
При вычитании 10-2=8, число 10 – уменьшаемое, 2 – вычитаемое, 8 – разность. При действиях с натуральными числами уменьшаемое не может быть меньше вычитаемого. Разность 2х чисел, показывает, на сколько первое число больше второго, или на сколько второе число меньше первого.
Свойства вычитания
1. Свойство вычитания суммы из числа.
Чтобы вычесть сумму из числа, надо вычесть из числа первое слагаемое, а потом из полученной разности – второе слагаемое.
Например: (6+3)-2=9-2=7
6+(3-2)=6+1=7
(6-2)+3=4+3=2.
2. Свойство вычитания числа из суммы.
Чтобы из суммы вычесть число, надо вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое.
Вычитаемое число должно быть меньше слагаемого, из которого его вычитают, или равно ему. Это свойство называют свойством вычитания числа из суммы.
3. Если из числа вычесть нуль, оно не изменится.
Например: 6-0=6
6+0=6.
4. Если из числа вычесть это число, получится нуль.
Например: 6-6=0.
Число, получаемое в результате выполнения всех указанных действий в числовом выражении, называют значением этого выражения. При решении задач записывают действия, а потом их выполняют. Полученные записи называют числовыми выражениями.
Например: 980+(980+50)=2010, 2010 – значение этого выражения.
Выражение, содержащее буквы, называют буквенным выражением. Числа, которыми заменяют букву, называют значениями этой буквы.
Буквенная запись свойств сложения и вычитания
Свойства сложения и вычитания можно записать с помощью букв.
1. Переместительное свойство сложения записывается так: а+b=b+а. В этом равенстве буквы а и в могут принимать любые натуральные значения и значение 0.
2. Сочетательное свойство сложения записывается так: а+(b+с)=а+b+с=а+b+с. Здесь, а, в, с – любые натуральные числа или нуль.
3. Свойство нуля при сложении записывается так: а+0=0+а=а. Здесь буква а может иметь любое значение.
4. Свойство вычитания суммы из числа записывается так: а-(b+с)=а-b-с. Здесь b+с<а или b+с=а.
5. Свойство вычитания числа из суммы записывается так: (а+b)-с=а+(b-с), если с<b, или с=b. (а+b)-с=(а-с)+b, если с<а или с=а.
6. Свойство нуля при вычитании записывается так: а-0=а, а-а=0. Здесь а может принимать любые натуральные значения и значение 0.
Умножение натуральных чисел и его свойства
Умножить число m на натуральное число n, значит найти сумму nслагаемых, каждое из которых равно m. Выражение m*n и значение этого выражения называют произведением чисел mи n. Числа m и n называют множителями. Произведения 7*4 и 4*7 равны одному и тому же числу.
1. Произведение 2х чисел не изменяется при перестановке множителей. Это свойство умножения называют переместительным. Например:
(5*3)*2=15*2 и 5*(3*2)=5*6. Одно и тоже значение 30. Значит 5*(3*2)=(5*3)*2.
2. Чтобы умножить число на произведение 2х чисел, надо сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель. Это свойство умножения называется сочетательным. d*(b*с)=(а*b)*с, 2*(3*с)=(2*3)*с. Сумма n слагаемых, каждое из которых равно 1, равна n. Поэтому верно равенство 1*n=n. Сумма n слагаемых, каждое из которых равно нулю, равна нулю. Поэтому равенство верно 0*n=0. Перед буквенным множителем обычно знак умножения не пишется, вместо 2*х пишут 2х.
Опускают знак умножения и перед скобками 2*(а+b) пишется 2(а+b). Когда в записи произведения нет скобок, умножение выполняется по порядку слева направо.
Делимость натуральных чисел и его свойства
Деление – это действие, с помощью которого по произведению и одному из множителей, находят другой множитель. 32:2=16. Число, которое делят называют делимым. Число, на которое делят, называют делителем, результат деления называют частным. Частное показывает, во сколько раз делимое больше, чем делитель.
Ни одно число нельзя делить на нуль.
- При деление любого числа на 1 получается это же число.
- При деление числа на это же число получается единица.
- При делении нуля на число получается нуль.
Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
Например: х:8=13
х=13*8=104, х – произведение множителей 8 и 13.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Чтобы найти неизвестное делимое, надо частное умножить на делитель, 42:х=6 42 – произведение множителей 6 и х, то есть 6х=42.
Деление одного натурального числа на другое нацело не всегда возможно, 22:4=5(2). Число 22 здесь делимое, 4 – делитель, 5 – неполное частное, и 2 остаток. Остаток всегда меньше делителя 2<4. Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка. Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток. Например: 22=(5*4)+2.
При делении m:n=k говорят, что m – делимое, n– делитель, k– частное число m называют также кратным числа n, а число n– делителем числа m. Если m – кратное числа n, то существует натуральное число k такое, что m=kn.
1. Чтобы найти наибольший делитель нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем.
2. Пусть даны числа 72 и 96. Выпишем все делители числа 72: 1,2,3,4,6,8,9,12,18,24,36,72. Выпишем все делители числа 96: 1,2,3,4,6,8,12,24. Среди выписанных чисел есть одинаковые: 1,2,3,4,6,8,12,24. Все эти числа называют общими делителями чисел 72 и 96, а наибольшим среди них – наибольшим общим делителем.
Например: Найти Д (3780, 7056)
Решение
3780=22*33*5*7
7056=24*32*72
Тогда Д (3780, 7056)=22*32*7, взяты простые множители, которые входят и в разложение числа 3780, и в разложение числа 7056.
Итак, Д(3780 и 7056)=252.
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим (из имеющихся) показателем.
Например. Пусть даны числа 12 и 18.
Кратные 12: 12,24,36,48,60,72.
Кратные 18: 18, 36,54,72.
Среди выписанных чисел есть одинаковые: 36,72. Все эти числа называют общими кратными чисел 12 и 18, а наименьшее из них число – 36 – называют наименьшим общим кратным чисел 12, 18.
Например: k(3780, 7056)
Решением имеем 3780=22*33*5*7
7056=24*32*72
Тогда k(3780, 7056)=24*32*72, то есть взяты все простые множители, которые входят в разложения хотя бы одного из чисел 3780 и 7056. Итак, k(3780,7056)=105840. Наименьшее общее кратное 2х взаимно простых чисел равно произведению этих чисел.
3. Например, найти Д (148,60,72). Разложим на простые множители каждого из данных чисел: 48=24 *3, 60=22*3*5, 72=23*32. Значит Д(48,60,72)=22*3. Получим: Д(48,60,72)=12.
Простые и составные числа
Простым называется натуральное число, не имеющее других делителей, кроме 1 и себя самого. Остальные натуральные числа, за исключением 1, называются составными. Натуральное число 1 не является ни простым, ни составным числом. Представление натурального числа n в виде произведения натуральных чисел n=b*с называется разложением на множители.
Для простых чисел – это разложение состоит только из самого числа. Если натуральное число составное, то можно единственным образом представить в виде произведения простых множителей. 19=1*19 При разложении чисел на простые множители используются признаки делимости и применяется запись столбиком, при котором делитель располагается справа от вертикальной черты, а частное записывается под делимым. Так, для числа 360 эта запись будет выглядеть следующим образом:
Это и есть основная теорема арифметики.
Из чисел с помощью знаков, арифметических действий и скобок составляют числовые выражения. Если в числовом выражении выполнить указанные действия, соблюдая принятый порядок, то получится число, которое называют значением выражения.
В некоторых случаях, не производя деления натурального числа m на натуральное число n можно ответить на вопрос: выполнимо деление m на n без остатка или нет? Ответ на этот вопрос можно получить с помощью различных признаков делимости:
Теорема 1. Если каждое слагаемое делится на некоторое число, то и сумма делится на это число (теорема о делимости суммы). Не следует, однако, думать, что если каждое слагаемое суммы не делится на какое – то число, то и сумма не делится на это число. Например, сумма 37+19 делится на 4, хотя ни 37, ни 19 не являются кратными числа 4. Заметим, однако, что если все слагаемые, кроме одного, делятся на некоторое число, то сумма не делится на это число.
Теорема 2. Если в произведении один из множителей хотя бы один из множителей делится на некоторое число, то и произведение делится на это число (теорема о делимости произведения). Например, не выполняя умножения, можно утверждать, что произведение 105*48*93*54 делится на 5, так как 105 делится на 5.
Теорема 3. Натуральное число делится на 2 тогда, и только тогда, когда его последняя цифра делится на 2 или равна нулю (признак делимости на 2). Числа, делящие на 2, называются честными и составляют множество честных натуральных чисел.
Теорема 4. Натуральное число делится на 5 тогда, и только тогда, когда его последняя цифра либо 0, либо 5 (признак делимости на 5).
Теорема 5.Натуральное число делится на 19 тогда, и только тогда, когда его последняя цифра 0 (признак делимости на 10).
Теорема 6. Натуральное число, содержащее не менее 3х цифр, делится на 4 двузначное число, образованное последними двумя цифрами заданного числа (признак делимости на 4). Например, число 15436 делится на 4, так как число 36 делится на 4. Число 372506 не делится на 4, так как 06, то есть 6 не делится на 4.
Теорема 7. Натуральное число делится на 3 тогда, и только тогда, когда сумма его цифр делится на 3. Например, число 2742 делится на 3, так как делится на 3 сумм цифр этого числа 2+7+4+2=15. Число 17941 не делится на 3, так как сумма цифр этого числа равна 22, а 22 не делится на 3.
Теорема 8. Натуральное число делится на 9 тогда, когда сумма его цифр делится на 9 (признак делимости на 9).
Занимательные факты о натуральных числах
Кроме ознакомления с теоретическим материалом моей задачей было подобрать занимательные факты из истории математики по решению древними учёными тех или иных задач с натуральными числами.
— Итак , я выяснила, что алфавитные системы нумерации позволяли легко обращаться с числами первой тысячи, а при помощи дополнительных знаков — в пределах десяти тысяч ( например, это было последнее число, имевшее у греков свое имя — мириада).
Классическая древность и не сталкивалась с необходимостью заглядывать дальше этой границы в каких-либо реальных или теоретических ситуациях. Неопределенные библейские выражения типа «тысячи тысяч», «тьма тем» (Дан. 7,10), «легион» (Лук. 8,30) или обыденное «как песчинок» отодвигали числовой горизонт в некоторую загадочную даль, невыразимую в конкретных количествах.
Но вскоре я обнаружила интересный факт: в заметке «Псаммит» (т.е. исчисление песка) Архимед показал, как можно систематически строить и называть сколь угодно большие числа. В частности, размещая в маковом зерне 10 000 (мириада) песчинок, он находит, что во Вселенной (шар диаметром в мириаду диаметров Земли) поместилось бы (в наших обозначениях) не более чем 1063 песчинок.
Любопытно, что современные подсчеты количества атомов в видимой Вселенной приводят к числу 1067 (всего в мириаду раз больше). Великий Архимед убедил, что он в состоянии указать некоторые числа, превосходящие число песчинок в объеме всей Вселенной. Но воображение его остановилось на жутком образе мира, утонувшего в пыли. Точно так же и безвестный служитель «цыфирной науки» ограничил полет своей терминологической фантазии колодой, устояв перед соблазном рассмотреть, скажем, «легион колод».
Математики не хотели изобретать большие числа свыше количества их, необходимого для тех или иных конкретных нужд. Натуральный ряд мыслился лишь потенциально бесконечным, т.е. неограниченно продолжаемым, а не существующим актуально, в качестве завершенного объекта. Таким образом, создавались все новые натуральные числа, а не открываем их, как острова в безбрежном океане.
На противоположной точке зрения стоял святой Августин (354-430), обличавший своих оппонентов в том, что они считают «будто бесконечность превышает знание Господне». С конца прошлого века математики постепенно склонялись к признанию бесконечных множеств как актуально существующих — независимо от того, описан ли как-нибудь способ их образования.
В современной математической практике эта точка зрения возобладала, но не все ее разделяют, и теоретические дискуссии об актуальной и потенциальной бесконечности продолжаются (а как вы воспринимаете натуральный ряд?)
— В 1955 году английский математик Скьюз показал, что существует натуральное число x, обладающее некоторым важным свойством (детали здесь несущественны), и что оно не превосходит величины 101010964. Число 101010964 в настоящий момент является наибольшим натуральным числом, использованным для какой-либо практической цели.
Его полная запись представила бы собой единицу с количеством нулей, заполняющим многие тома. И архимедово число песчинок, и число атомов во Вселенной, и даже «великое славянское число» колода не сопоставимы с этим монстром, обозначающим сегодняшнюю границу потенциально бесконечного натурального ряда.
— Главная книга христианского мира Библия в полной мере отражает ту роль, которую играли разнообразные вычисления в жизни наших далеких предков. В пятой главе книги «Бытие» указываются потомки Адама от Сифа до Ноя. Стандартная конструкция этой главы имеет следующий вид: «25 Мафусаил жил сто восемьдесят семь лет, и родил Ламеха. 26 По рождении Ламеха, Мафусаил жил семьсот восемьдесят два года, и родил сынов и дочерей. 27 Всех же дней Мафусаила было девятьсот шестьдесят девять лет; и он умер.» Согласимся, что арифметические примеры типа 187+782=969 никак нельзя считать тривиальными для времени создания Библии.
В главе 11 «Бытия» после рассказа о крушении Вавилонской башни приводится список потомков Сима, старшего сына Ноя, однако здесь общая схема дается в усеченном виде: «24 Нахор жил двадцать девять лет, и родил Фарру. 25 По рождении Фарры, Нахор жил сто девятнадцать лет, и родил сынов и дочерей. Финальный возраст Нахора не указывается, интересующемуся придется искать сумму 29+119.
— В книге «Числа» (название говорит само за себя) приводятся статистические сведения о числе всех сынов Израилевых, годных для войны, во всех коленах, о распределении воинов каждого колена по станам. Здесь уже приходится иметь дело с величинами вроде 46 500, 59 300, 64 400, а общее количество всех военнообязанных достигает 603 550 при первом обследовании (глава 1) и 601 730 при втором (глава 26). В главе 31 (стихи 26-47) рассматривается сложный пример деления военной добычи. Он не вполне завершен и мог бы послужить предметом интересных обсуждений.
Разнообразные подсчеты и измерения проводятся в книгах Иисуса Навина (глава 21), 1-й Паралипоменон (главы 12, 15), Ездры (главы 1, 2, 8), Неемии (глава 7), Иеремии (глава 52), Иезекииля (глава 40). Наибольшее конкретное число указывается во второй книге Царств (глава 24): 800 000. И, конечно, нельзя не упомянуть об Откровении святого Иоанна Богослова (Апокалипсис), где в заключительном стихе главы 13 указывается «число зверя»: 666 (или римскими цифрами: DCLXVI — шесть разных цифр в правильном порядке! Кроме того, 666 — это сумма первых 36 натуральных чисел).
В различные исторические периоды пытливые умы, применяя реальные или изобретенные к случаю алфавитные нумерации, пытались разоблачить тех или иных деятелей путем «расшифровки» их имен и титулов так, чтобы получилось роковое число. Вот и Пьер Безухов («Война и мир», т.3, часть 1, глава XIX), приписав числовые значения буквам французского алфавита, нашел, что L’empereur Napoleon дает 666 «и что поэтому Наполеон и есть тот зверь, о котором предсказано в Апокалипсисе».
Несмотря на некоторые погрешности (пропуск буквы j в алфавите, арифметическая ошибка, исправляя которую, приходится писать Le empereur), апокалиптические вычисления Пьера, троекратно приводящие к числу 666, изумляют.
Заключение
Вот и закончилось моё исследование на тему «Натуральные числа». Готовя своё исследование, я узнала много нового и интересного о числах, о высказываниях математиков, учёных, живущих в разные века и время.
Эта тема очень обширная и писать можно о числах бесконечно. Чем глубже проникаем в изучение математики, тем больше находим интересных и полезных для себя сведений об этой науке и теме «Натуральные числа».
Математика, скорее всего, никогда не достигла бы такой великой степени совершенства, если бы древние не приложили столько усилий для изучения проблем, которые сегодня воспринимаются нами как истина. Как часто новые методы, новая техника или алгоритм, возникшие при решении, казалось бы, частных задач, приводили науку на новый, более высокий уровень развития!
Без знаний по математики, без знания о натуральных числах, о счёте чисел, мы не смогли бы добиться больших успехов в технике, изобретении, научных открытиях и создании сложных вычислений.
Я буду постоянно следить за литературой о математике, о новых событиях в науке, а также изучать историю математики, работы выдающихся математиков.
Не слишком ли много внимания я уделила начальным шагам в математику? Ответом на это мог бы послужить известный афоризм немецкого математика Леопольда Кронекера (1823-1891): «Бог создал натуральные числа, все остальное — дело рук человеческих»…
Список литературы
- Большая школьная энциклопедия г. Москва 2004г. «Русское энциклопедическое творчество».
- Справочник школьника г. Москва 2004г. Авторы: В.А.Гусев и А.Г.Мордкович.
- Математика – учебник для общеобразовательных учреждений г. Москва 2003г. Авторы: А. Мордкович. Из – во Мнемозина
- Математика. Г. Москва 1992 г. Авторы: И.
Если страница Вам понравилась, поделитесь в социальных сетях:
Цель урока: развитие устойчивого
интереса к математике.
Воспитательная цель: формирование
коммуникативных навыков и волевых качеств
личности.
Задачи:
- Закрепить и развить навыки выполнения
арифметических действий с натуральными числами; - Продолжить работу по формированию навыков
решения уравнений; - Развивать умение решать текстовые задачи с
практическим содержанием, логические задачи.
Оборудование урока: ТСО,
дидактический раздаточный материал, рисунки к
заданиям.
Форма проведения урока:
сказка-соревнование.
Правила игры:
- Учащиеся разбиваются на две команды;
- Команды отвечают на вопросы письменно;
- Побеждает в игре та команда, которая больше
наберет баллов.
Ход урока
“Горят причудливо краски,
И, как ни мудра голова,
Вы все-таки верьте сказке,
Сказка всегда права”.
Вступительное слово учителя:
Повторение темы “Натуральные числа” пройдет
на основе сюжета сказки Алексея Толстого
“Приключения Буратино”. Вместе с героем сказки
Буратино мы совершим путешествие по стране
чисел.
Цель игры: вместе с Буратино преодолеть
трудности, успешно справиться с заданиями и
найти золотой _ _ _ _ _ _. Итак: выполните действия,
применяя свойства сложения и вычитания, и
узнайте, что хочет найти Буратино.
- (311+44)-211=
- (236+417)-117=
- 1441-(326+441)=
- 146-(31+46)=
- (36+19)+44=
- 458+317+42=
Ответы: 536-л, 144-к, 69-ч, 23-м, 817-к, 674-ю.
Выполнено задание и мы узнали, что Буратино
утром решил отправиться на поиски ключика.
Буратино- мальчик шустрый, но деревянный, поэтому
ему нужна ваша помощь!
1 этап пути
- Задание 1. Буратино лег спать пораньше, в семь
часов вечера, предварительно заведя будильник на
восемь часов с тем, чтобы встать утром. Сколько
часов он проспал, пока его не разбудил будильник.
(1 час). - Задание 2. У Буратино в шкафу лежали в вперемежку
три пары носков с красными полосками и четыре
пары с желтыми полосками. Какое наименьшее число
носков он должен взять из шкафа в темноте, чтобы
иметь не менее пары носков одного цвета? ( 3 носка).
2 этап пути
Утром Буратино отправился в путь на поиски
ключика, который хранится у старой черепахи
Тортилы. Дорога предстояла трудная и далекая.
На окраине города внимание Буратино привлекла
харчевня “Три пескаря”. Проголодавшийся
Буратино решил подкрепиться.
В харчевне он увидел Карабаса Барабаса, лису
Алису и кота Базилио. На вертеле жарилась утка, но
у Буратино не было денег. Карабас Барабас
предложил ему пойти на сделку. Если Буратино
правильно отвечает на вопрос, то его накормят
бесплатно и дадут несколько золотых монет.
- Задание 3. Одна утка на вертеле жарится до
готовности один час. За сколько часов на одном
вертеле зажарятся сразу три утки? (один час).
3 этап пути
Сытый Буратино продолжил путь . За городом он
увидел красивую лужайку и посреди неё маленький
домик. В нем жила Мальвина, девочка с голубыми
волосами. Мальвина рассказала Буратино о том, что
вдоль каждой дороги написано уравнение. Нужно
найти корни уравнений и определить путь, ведущий
к пруду черепахи Тортилы.
Поможем Буратино справиться с этим трудным
заданием.
- Задание 4. Решите уравнения.
- 7х+21=133 (х=16).
- 181-8х=45 (х=17).
- 162:х=9 (х=18).
К пруду Тортилы вел указатель с числом 16,
поэтому Буратино пошел по первой дороге.
4 этап пути
Буратино продолжил путь. Лиса Алиса и кот
Базилио решили заманить Буратино в Страну
Дураков.
- Задание 5. Они привели Буратино на пустырь и
рассказали:
— это Поле Чудес: если закопаешь здесь золотые
монеты, то утром вырастит дерево, на котором
будет в три раза больше золотых монет. Затем все
это можно повторить. Так можно снять несколько
урожаев. Закопай свои монеты, а мы можем
посторожить их.
В награду за услуги Лиса Алиса и кот Базилио
потребовали после каждого урожая отдавать по 9
монет. Буратино не согласился. Он заявил, что
после двух урожаев у него совсем не останется
денег. Сколько золотых монет было у Буратино?
(четыре монеты).
5 этап пути
Буратино бежал из Страны Дураков и продолжил
путь через топкое болото. Следуем за Буратино по
математическим кочкам. Поможем преодолеть
очередное препятствие Буратино.
- Задание 6. Выполните действия
6 этап пути
Наконец-то, Буратино подошел к пруду, в котором
живут черепаха Тортила и много-много зеленых
лягушек. Лягушки довезли на кувшинке Буратино до
черепахи. Черепаха Тортила тоже загадала загадку
Буратино.
- Задание 7. Буратино вынесли 3 шкатулки. На одной
написано “Здесь лежит золотой ключик”, на
другой “Непустая шкатулка”, в третьей “Здесь
сидит черепаха”. Все надписи неверны. Где же
лежит золотой ключик? (в третьей).
Получив ключик, довольный Буратино вернулся
домой….
Итоги игры.
Сегодня на уроке вы, ребята, преодолели много
испытаний. За помощь Буратино всем большое
спасибо! Объявляются результаты игры. Участники
игры за урок получают оценки.
Представим себе такую историю…
Раз, два, три, четыре, пять,
Научились мы считать.
Ну а дальше мы не знаем,
Может, вместе посчитаем?
Шесть – конфеты любим есть,
Семь – мы помогаем всем,
Восемь – мы друзей в беде не бросим,
Девять – учимся на пять,
Десять – кончили считать.
Вспоминал считалочку Саша.

– Саша, а что ты делаешь? Для чего это ты
считаешь? – спросил Паша.
– Я хочу привести в порядок свою коллекцию
солдатиков! Как из них всех выбрать кого-то на первое место? Они же такие все
одинаковые! – воскликнул Саша.

– Я совсем не вижу проблемы! Посмотри: на
каждом из твоих солдатиков стоит цифра. Ну так и поставь их по порядку! –
возразил Паша.
– Как это? Что значит по порядку? – удивился
Саша.
– Саша, ты такой смешной! Ты что, в школе не
изучал натуральные числа? – с недоумением спросил Паша.
– Какие числа? На-ту-раль-ные??? – ещё больше запутался Саша.
– Да, да, Саша! Именно натуральные! –
продолжил Паша. Давай я тебя познакомлю со своим другом Электрошей.
И он сейчас тебе всё объяснит.
– Мы каждый день отвечаем на вопрос «Сколько?»
– начал Электроша. При этом, помимо слов «много» или
«мало», мы называем конкретные числа. Кстати, а вы знаете, что число является
основным понятием математики, которое сложилось в ходе очень длительного
исторического развития? А чтобы ответить на вопрос «Сколько?», надо сосчитать.

– Вот, Саша, сколько тебе лет? – спросил Электроша.
– Одиннадцать! – уверенно ответил Саша.
– Все те числа, которые вы слышите с самого
рождения, и, кстати, они же будут сопровождать вас постоянно и повсюду,
помогают нам считать различные предметы и отвечают на вопрос «Сколько?» –
продолжал Электроша. –Такие числа называются натуральными.

Запомните! Числа 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12 и так далее, используемые при счёте предметов, называют
натуральными.

Вот, например, числа 1, 5, 7, 11, 31, 365, 2017,
1 000 000 – это натуральные числа. Но важно понимать, что не
все числа, которыми вы пользуетесь, – натуральные. Так, например, числа 0,  ,
,  ,
, 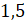 – не являются натуральными числами. Об этих
– не являются натуральными числами. Об этих
числах мы поговорим в другой раз.

Вообще, название «натуральное»
происходит от латинского слова natura –
‘природа’. То есть натуральные числа как бы происходят от природы, но,
конечно, изобретены они человеческим мозгом.

Впервые термин «натуральное число»
появился в трудах римского философа Боэция, жившего ещё в V – VI веках.

– Спасибо, Электроша!
– с радостью воскликнул Саша. – Теперь я всё понял и могу с лёгкостью привести
в порядок свою коллекцию солдатиков. И тут Саша быстренько начал расставлять
солдатиков по своему порядку.

– Саша, ты не всё понял! – остановил Сашу
Паша. – Ведь числа тоже имеют свой порядок.
– Порядок? – удивился Саша.
– Да, Саша! Числа тоже хотят жить в порядке! –
сказал Электроша.
Если выстроить все числа по порядку, только
не просто, как ты сейчас расставил своих солдатиков, а от меньшего числа к
большему, то получится натуральный ряд.
Запомните! Все натуральные числа,
записанные в порядке возрастания, образуют ряд натуральных чисел
(или натуральный ряд).

А вот что тебе ещё нужно знать о натуральном
ряде:
1) натуральный ряд чисел начинается с числа 1.
То есть первым числом натурального ряда является число 1, вторым – число 2,
третьим – число 3 и так далее;
2) в натуральном ряду за каждым числом
следует ещё одно число, большее предыдущего на единицу. То есть для того, чтобы
получить следующее натуральное число, надо прибавить к текущему натуральному
числу единицу;
3) число один не имеет предыдущего. Значит,
мы можем с уверенностью говорить, что среди натуральных чисел есть наименьшее
число – и это число 1, но нет наибольшего;
4) в натуральном ряду чисел нет последнего
числа. Другими словами, натуральный ряд чисел бесконечен, так как к любому
числу всегда можно прибавить ещё единицу;
5) натуральных чисел бесконечно много, а вот
несуществующих предметов человеку не приходило в голову считать. Поэтому число ноль
не натуральное число, так как оно не может получиться в результате счёта;
6) выписать весь натуральный ряд невозможно.
Обычно поступают так: выписывают подряд несколько первых чисел натурального
ряда, а затем ставят многоточие.

– Вот теперь, Электроша,
я точно всё понял – обрадовался Саша. – Посмотри, как я расставил своих
солдатиков!

– Да, Саша, на этот раз ты сделал всё
правильно! – подбодрил Электроша Сашу. – И раз ты всё
понял, предлагаю вам с Пашей закрепить знания на выполнении некоторых заданий.
Задание первое: из указанных чисел выберите
натуральные.
11,  , 251, 0, 12 800.
, 251, 0, 12 800.
Решение: числа 11, 251, 12 800 –
натуральные, так как мы их используем при счёте, а вот те числа, которые
остались, не будут натуральными.

Следующее задание: из записанных рядов чисел
назовите натуральный.
0, 1, 2, 3, 4, 5, 6, 7, …
1, 2, 3, 4, 5, 6, 7, …
7, 6, 5, 4, 3, 2, 1, …
1, 3, 5, 7, 9, 11, …
Решение: в этом задании из всех записанных
числовых рядов натуральным будет только второй ряд. Первый ряд не подходит,
потому что вначале стоит цифра 0, а мы знаем, что 0 не является натуральным
числом. Третий ряд не подходит, так как числа записаны в нём не в порядке
возрастания, а в порядке убывания. А вот последний ряд не подходит, потому что
в нём каждое последующее число больше предыдущего не на единицу, а на два.

– Саша, Паша, вы отлично справляетесь с
заданиями! – с радостью сказал Электроша. – А значит,
вы обязательно справитесь с моей непростой задачей.
Задача. 11 коров за 3 дня съедают 33 мешка сена. Сколько мешков
сена надо 5 коровам на 5 дней?
Решение: сначала нам нужно найти, сколько
мешков сена съедают 11 коров за один день. Для этого 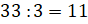 (м.).
(м.).
Затем мы можем узнать, сколько мешков сена
съедает 1 корова за 1 день. Для этого 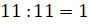 (м.). Получаем, что 1 корова за 1 день съедает 1 мешок сена.
(м.). Получаем, что 1 корова за 1 день съедает 1 мешок сена.
Теперь узнаем, сколько мешков сена съедят 5 коров
за 1 день. Для этого 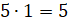 (м.) –– получаем 5 мешков сена.
(м.) –– получаем 5 мешков сена.
И осталось выяснить, сколько мешков сена
съедят 5 коров за 5 дней. Для этого 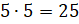 (м.).
(м.).
Получается, что 5 коров за 5 дней съедят 25 мешков сена.