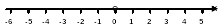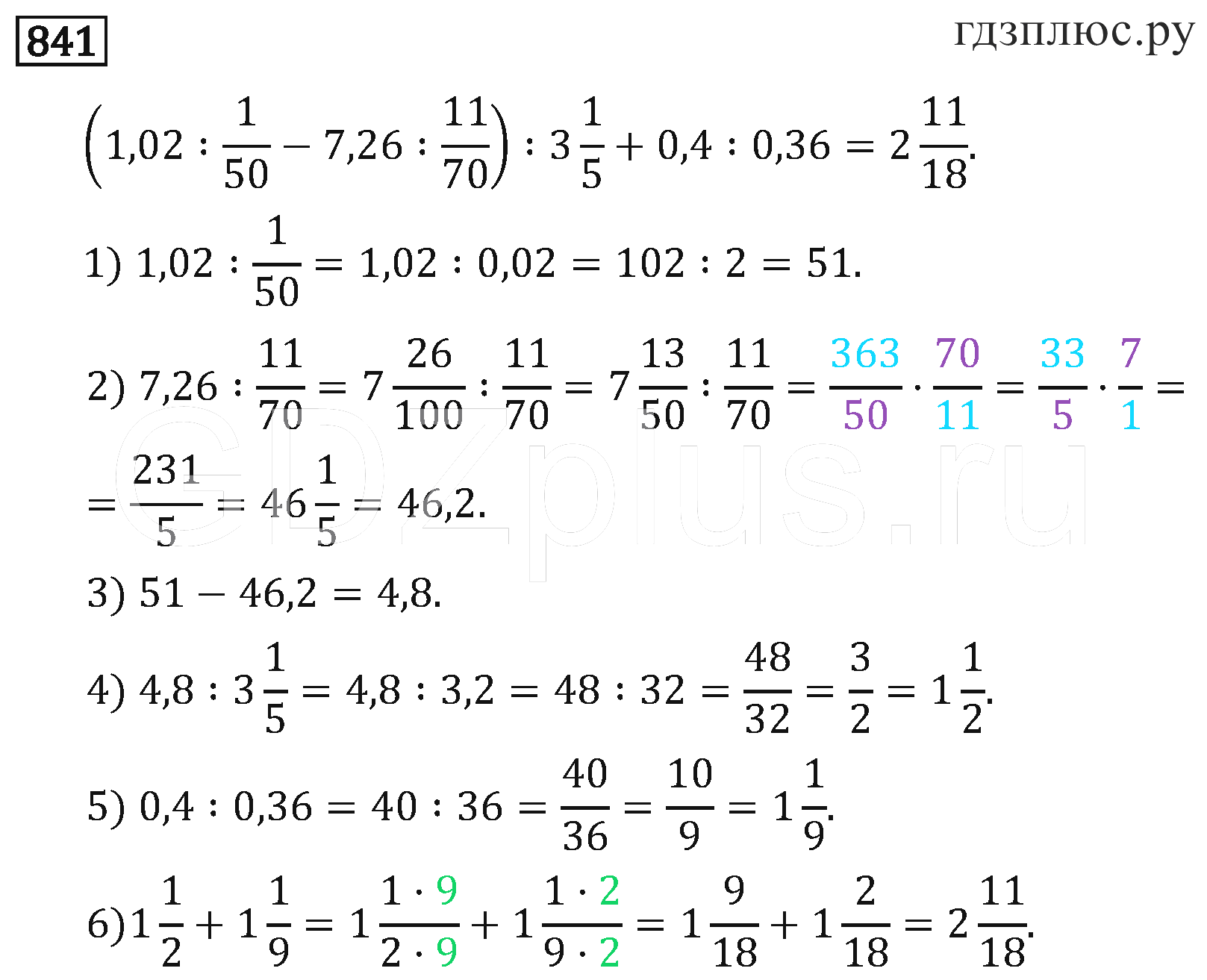Знакомство с положительными и отрицательными числами. Чем они отличаются. Как обозначаются.
Герасимова Татьяна Анатольевна
Урок № 92
Тема: «Изображение чисел на координатной прямой. Появление нуля и отрицательных чисел в математике древности»
6а –
6б –
6г –
6е –
6м —
Тип урока: ознакомление с новым материалом
Цель урока: формирование представления о координатной прямой.
Задачи урока:
Обучающая: дать всестороннее представление о новых числах, научить читать и записывать положительные и отрицательные числа, изображать их точками на прямой; определять координаты точек, находить координату точки, отмечать на координатной прямой точку по ее координатам.
Воспитательная: воспитывать добросовестность, усидчивость, целеустремленность, умение слушать, инициативность, активность.
Развивающая: развивать грамотную математическую речь, память, внимание, логическое мышление.
Планируемые результаты:
Предметные: знакомятся с понятиями положительные и отрицательные числа, изображают их на координатной прямой, определяют координаты точек.
Личностные: Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают оценку результатов своей учебной деятельности.
Метапредметные:
Р – определяют цель учебной деятельности, осуществляют поиск средств её осуществления.
П – делают предположения об информации, которая нужна для решения учебной задачи.
К – умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами.
Оборудование: мультимедийный проектор, компьютер, интерактивная доска.
Структура урока:
| 1. | Организационный момент | 2 мин |
| 2. | Анализ контрольной работы | 10 мин |
| 3. | Воспроизведение и коррекция опорных знаний через устный счет | 5 мин |
| 4. | Сообщение темы и цели урока | 1 мин |
| 5. | Ознакомление с новым материалом | 9 мин |
| 6. | Физкультминутка | 1 мин |
| 7. | Первичное осмысление и закрепление связей и отношений в объектах изучения | 10мин |
| 8. | Рефлексия | 2 мин |
| 9. | Постановка Д/З | 1 мин |
Ход урока
| Учитель | Ученики | УУД |
| ||
| Приветствую учащихся. Сажаю их на места. | Приветствуют учителя. | К: Умение слушать и вступать в диалог. |
| 2. Анализ контрольной работы | ||
| 1. Сообщить результаты контрольной работы. 2. Решить задания, вызвавшие затруднения у обучающихся. | Спрашивают. | |
| 3.Воспроизведение и коррекция опорных знаний через устный счет | ||
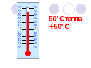
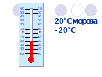
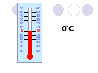
| — Где в практической жизни мы встречаемся с величинами, которые могут изменяться в противоположных направлениях? (слайд 1) Какую температуру показывает каждый термометр? (слайд 2 ) (слайд 3) (слайд 4) (слайд 5) (слайд 6) — Как называют температуру выше нуля? (слайд 7) — А как называют температуру ниже нуля? (слайд — На уроках математики до сих пор мы рассматривали натуральные и дробные числа. Однако в жизни вы уже наверняка встречались и с другими числами – отрицательными. Как вы думаете, какие числа мы называем положительные, а какие отрицательные? — Помимо положительных и отрицательных чисел, еще есть число 0. Как вы думаете, к каким числам оно относится? — Приведите примеры положительных и отрицательных чисел. (слайд 9) — Дело в том, что существует много вещей, которые могут, как увеличиваться, так и уменьшаться. Если на товар большой спрос, то завод увеличивает план по его выпуску, а если товар вышел из моды, то план уменьшают. Увеличивается и уменьшается с течением времени температура воздуха. Для описания изменения величин как раз и служат положит. и отрица. числа. Если величина растет, то говорят, что ее изменение «+», а если она убывает, то изменение называют «-». — Где применяют отрицательные числа? Зачем они нам нужны? (слайд 10) (слайд 11 — 13) История отрицательных чисел
— Давайте вспомним, что такое координатный луч? (слайд 14) 0 А(3) С(7) Точка А(3) расположена на расстоянии 3 правее начала луча Точка С(7) расположена на расстоянии 7 правее начала луча — Как построить точку М(-3) ? — С какой проблемой мы столкнулись? | Тепло — холод, влево — вправо, вверх — вниз, наличие денег – долг и т.д. +350С + 500С — 100С — 20 0С 0 0С положительная отрицательная — числа со знаком «+» называются положительными, а со знаком « — » отрицательными — 0 не относится ни к положит., ни к отрицат. Приводят примеры Слушают Отвечают слушают — это луч, с заданным полож.направлением, началом отсчета и ед.отрезком. — высказывают предположения | П: уметь ориентироваться в своей системе знаний К: уметь слушать и понимать речь других, оформлять мысли в устной речи Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение |
| 3. Сообщение темы и цели урока (слайд 15) | ||
| — Сформулируйте тему и цель сегодняшнего урока. Запишите тему урока в тетрадь. | — записывают в тетрадях число, кл/р, тема урока | |
| 4. Ознакомление с новым материалом | ||
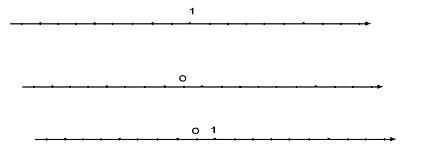
| Практическая работа 1. Начертите горизонтальную прямую 2. Отметьте на ней точку О (примерно посередине). Эту точку будем называть начало отсчета. 3. Выберите единичный отрезок и отложите его вправо и влево от начала отсчета (одну или две клетки). 4. Под каждой точкой подпишите соответствующие числа. — Чем неудобна эта шкала? — Как выйти из этого затруднения? В математике принято числа, которые идут влево от начала отсчета, записывать со знаком “- “. Направление вправо от начала отсчета называется положительным, и положительное направление на прямой обозначается стрелкой. Направление влево от точки О называется отрицательным (отрицательное направление не указывается). — Рассмотрим это еще раз (слайд 16 — 17). Точка О на прямой АВ разбивает эту прямую на два дополнительных луча ОА и ОВ. Точка О — начало отсчета. М(-3) М(3) 3 3 Выберем единичный отрезок. Положение точки на каждом из лучей задается ее координатой. Точка С(3) расположена на расстоянии 3 правее точки О. Точка М(-3) расположена на расстоянии 3 левее точки О. — Так что же такое координатная прямая? (слайд 18) Прямую с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой. — Что называется координатой прямой? Число, показывающее положение точки на прямой, называют координатой этой точки. Числа, расположенные справа от точки О называются положительными, а числа, расположенные слева от точки О называются отрицательными. Число ноль не относится ни к положительным числам, ни к отрицательным. (слайд 19) Задание: назвать среди этих прямых прямую, которая является координатной. (слайд 20) | Выполняют в тетрадях, учитель на доске — одно и тоже число стоит под двумя разными точками Смотрят и слушают отвечают записывают записывают Отвечают с места по одному | П: уметь добывать новые знания. Р: уметь работать по коллективно составленному плану, проговаривать последовательность действий на уроке. К: уметь слушать и понимать других, оформлять свои мысли в устной и письменной речи |
| 6. Физкультминутка (слайд 21) | ||
| А теперь, ребята, встали. Быстро руки вверх подняли, В стороны, вперед, назад. Повернулись вправо, влево, Тихо сели, вновь за дело. | Выполняют | |
| 7. Первичное осмысление и закрепление связей и отношений в объектах изучения | ||
| № 830 (устно) № 831 № 832 № 833 № 835 а) +6; б) -4 № 836 № 838 № 841 | С места по цепочке. Один ученик у доски, остальные в тетрадях С места по цепочке. Один ученик у доски, остальные в тетрадях | П: делают предположения об информации, которая нужна для решения учебной задачи. К: умеют критично относиться к своему мнению Р: понимают причины своего неуспеха и находят пути выхода из него. |
| 8. Рефлексия | ||
| — Закончите предложения.
| Поднимают руки. | Р: умеют оценивать правильность выполнения действий |
| 9. Постановка Д/З | ||
| П. 29, № 834, 837, 839, 840, 843 | Слушают, записывают. | |
4
-75%
Сохранить у себя:

Числа в пословицах, поговорках и сказках.ppt
Содержание:
1. Введение.
2. Из истории пословиц и поговорок.
3. Волшебные числа в произведениях устного народного творчества.
Число 1 в пословицах, поговорках и сказках
Число 2 в пословицах, поговорках и сказках
Число 3 в пословицах, поговорках и сказках
Число 4 в сказках
Число 7 в пословицах, поговорках и сказках
Число 9 в пословицах и поговорках
Число 12 в пословицах, поговорках и сказках
Число 13 в пословицах и поговорках
4. Заключение. Выводы по работе.
5. Источники информации.
При изучении русского фольклора, мы заметили, что в пословицах, поговорках и сказках очень часто употребляются числа.
Почему числа нашли свое отражение в русских пословицах, поговорках и сказках?
Какова их роль в устном народном творчестве?
Цель: Исследовать пословицы, поговорки и сказки в которых есть числа.
Гипотеза: Числа в пословицах, поговорках и сказках имеют магический смысл.
Задачи
1. Провести анализ литературы с целью выявления и классификации пословиц и сказок с числами.
2. Определить, каким числам народная мудрость посвятила больше пословиц, поговорок и сказок.
3. Систематизировать пословицы и сказки с числами 1,2,3,4,7,9,12,13,100.
Из истории пословиц и поговорок
У русского народа существует огромное множество пословиц и поговорок. Трудно сказать, с каких времён среди народа начали ходить пословицы и поговорки. Появились они ещё в то время, когда не было письменности.
Пословицы – краткие народные изречения с назидательным содержанием, народные афоризмы. В пословице есть второй смысл, это аллегория.
Чем дальше в лес, тем больше дров
У пословицы есть родная сестра – поговорка. Они похожи друг на друга. Поговорки – краткие устойчивые выражения, не составляющие, в отличие от пословиц, законченных высказываний.
Семь пятниц на неделе
«Поговорка – цветок, пословица – ягодка».
Самый большой сборник пословиц принадлежит Владимиру Ивановичу Далю
Волшебные числа в произведениях устного народного творчества
Народ очень часто употреблял в пословицах и поговорках числа. У каждого народа свой набор числовых символов.
Мы провели опрос 27 учащихся 5,6,7 классов и выяснили:
| № п/п | Вопрос | Варианты ответов |
| 1. | Знаете ли вы пословицы и поговорки, в которых есть числа? | Да – 89% |
| 2. | Какие числа чаще всего встречаются в пословицах и поговорках? | «1» — 44% |
| 3. | Приведите примеры пословиц с числами. | Один в поле не воин – 11 чел. |
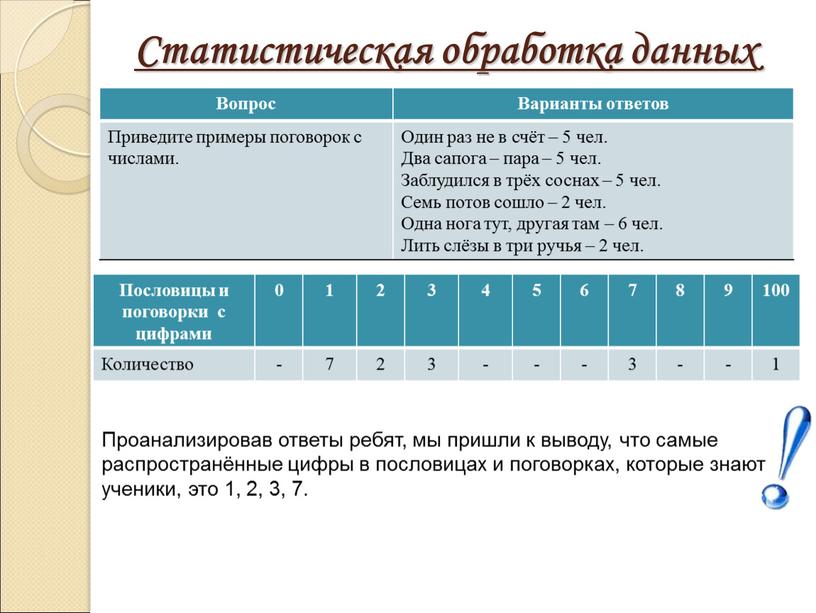
Статистическая обработка данных
| Вопрос | Варианты ответов |
| Приведите примеры поговорок с числами. | Один раз не в счёт – 5 чел. |
| Пословицы и поговорки с цифрами | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 100 | |
| Количество | — | 7 | 2 | 3 | — | 3 | — | 1 | |||
Проанализировав ответы ребят, мы пришли к выводу, что самые распространённые цифры в пословицах и поговорках, которые знают ученики, это 1, 2, 3, 7.
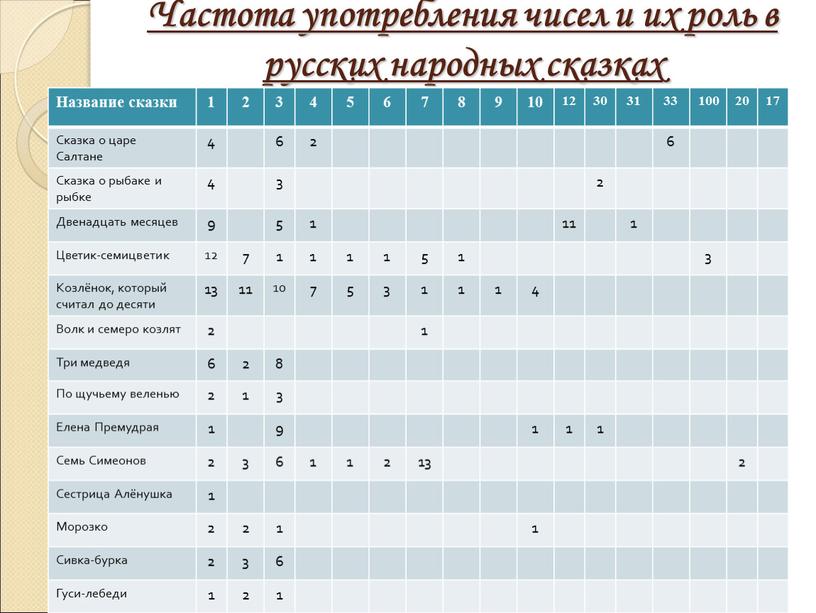
Частота употребления чисел и их роль в русских народных сказках
| Название сказки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 30 | 31 | 33 | 100 | 20 | 17 |
| Сказка о царе Салтане | 4 | 6 | 2 | 6 | |||||||||||||
| Сказка о рыбаке и рыбке | 3 | 2 | |||||||||||||||
| Двенадцать месяцев | 9 | 5 | 1 | 11 | 1 | ||||||||||||
| Цветик-семицветик | 12 | 7 | 1 | 5 | 1 | 3 | |||||||||||
| Козлёнок, который считал до десяти | 13 | 11 | 10 | 7 | 5 | 3 | 1 | 4 | |||||||||
| Волк и семеро козлят | 2 | ||||||||||||||||
| Три медведя | 6 | 2 | 8 | ||||||||||||||
| По щучьему веленью | 2 | 1 | 3 | ||||||||||||||
| Елена Премудрая | 1 | 9 | 1 | ||||||||||||||
| Семь Симеонов | 2 | 3 | 6 | 1 | 2 | 13 | 2 | ||||||||||
| Сестрица Алёнушка | 1 | ||||||||||||||||
| Морозко | 2 | 1 | 1 | ||||||||||||||
| Сивка-бурка | 3 | 6 | |||||||||||||||
| Гуси-лебеди | 1 | 2 | 1 | ||||||||||||||
| Название сказки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 30 | 31 | 33 | 100 | 20 | 17 |
| Волк и лисица | 1 | 1 | |||||||||||||||
| Царевна-лягушка | 2 | 6 | 1 | 1 | 1 | ||||||||||||
| Курочка Ряба | |||||||||||||||||
| Сказка о золотом петушке | 1 | 2 | |||||||||||||||
| Сказка о мёртвой царевне | 2 | 1 | 2 | 1 | |||||||||||||
| Иван-царевич и серый волк | 5 | ||||||||||||||||
Мы составили таблицу частот чисел, которые встречаются в сказках. В рассмотренных текстах 20 русских народных сказок числа встречаются 264 раза.
Первые места в рейтинге заняли числа: «3», «1», «2», «7».
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 30 | 31 | 33 | 100 | 20 | 17 |
| Частота употребления | 69 | 33 | 73 | 13 | 8 | 7 | 22 | 2 | 7 | 12 | 3 | 1 | 6 | 3 | 2 | 1 | |
Возникает вопрос: « Почему чаще всего встречаются числа 3 и 1?»
Оказывается Пифагор и его единомышленники ставили единицу выше всех других чисел, считая, что именно она начало всех начал. Что именно от неё пошёл весь мир. И, правда, единица – «героиня» и «прима» всякого счёта. Та самая, о которой говорят: «Мал, да удал»! Без единицы не состоялось бы самое простое исчисление.
Число три символизирует собой целостность, тройственную природу Мира, его разносторонность, триединство созидающих, разрушающих и сохраняющих сил Природы – примиряющее и уравновешивающие их начало, счастливую Гармонию, творческое совершенство и удачу. Тройка на Руси считалась воплощением духовного начала. Как и в европейской культуре, она символизирует полноту и завершённость.
Квадрат Пифагора. Нумерология для всех.
Пословицы и поговорки с числом 1
Единица – изобретение математиков, она нужна для счета, и в магии чисел ее не существует. В древних текстах слово «один» употребляется нечасто и означает нечто неделимое, целостное, такое, как Бог, Космос, Вселенная.
А в некоторых пословицах единица означает что-то очень малое, незначительное.
Один в поле не воин.
Один в море не рыбак.
Семь бед — один ответ.
Один за всех и все за одного.
Лучше один раз увидеть, чем сто раз услышать.
В страду одна забота – не стояла бы работа.
От великого до смешного – один шаг.
Одна голова – хорошо, а две лучше.
Один дурак пятерых умных ссорит.
Одна голова – два языка.
Значение чисел в сказках — число 1
С давних пор люди наделяли цифры особым магическим значением. Если мы вернемся к устному народному творчеству, то увидим, что все сказки, былины и предания были пронизаны числовой символикой. Число 1 встречается в сказках очень часто. Например, один -одинешенек Кузьма скоробогатый, одна сиротинушка маленькая Крошечка — Хаврошечка. Зачастую цифра 1 символизирует одного человека, главного героя, которому придется бороться с обстоятельствами, своими страхами, вымышленными, либо реальными злодеями. Подобная фигура весьма целостная, самодостаточная. Это становится понятно, если мы обратимся к значению числа 1 и увидим, что оно отождествляется с единством, сосредоточением силы в одном источнике.
Пословицы и поговорки с числом 2
В магии числа Двойка как бы есть, но вроде ее нет. Просто деление на свет и тьму. Это знак сравнения одного с другим. А еще Двойка – символ взаимоотношений и взаимодействий человека с тем, что его окружает.
Старый друг лучше новых двух.
Два медведя в одной берлоге не уживутся.
За двумя зайцами погонишься — ни одного не поймаешь.
Два сапога – пара.
Одна голова – хорошо, а две лучше.
Скупой платит дважды.
Убить двух зайцев.
Двум смертям не бывать, а одной не миновать.
Лентяй да шалопай – два родных брата.
Из двух зол выбирай меньшее.
За битого двух небитых дают.
Символическое значение числа 2
Как часто в сказках встречается цифра 2? Например, в сказке «Гуси-лебеди» были дочка да сынок (двое детей), в «Морозко» падчерица и родная дочка, в сказке «Про ленивую и радивую» главные героини —две дочери. Практически всегда эта цифра является символом парности, показывает читателю двух абсолютно противоположных персонажей. Символика числа 2 указывает на двойственность всего. Например, есть живая и мертвая вода, день и ночь, утро и вечер, небо и земля, добро и зло, правда и кривда. Подобные противоположности демонстрирует большинство народных сказок, дошедших до нашего времени. Самая частая противоположность — добро в образе главного героя побеждает зло в образе своего недруга или обидчика.
Пословицы и поговорки с числом 3
Три – первое в магическом ряду число. Оно открывает настоящий магический счет, с ним появляется что – то действительно новое. Время мы делим на три – прошлое, настоящее, будущее, пространство мы делим на три – ширину, длину, высоту. Число три у многих народов священное.
Заблудиться в трёх соснах.
Бог любит троицу.
У мужика в августе три заботы: и косить, и пахать, и сеять.
Не узнавай друга в три дня – узнавай в три года.
Обещанного три года ждут.
От горшка три вершка.
Наврал с три короба.
Плакать в три ручья.
Согнуться в три погибели.
Почему в русских сказках часто используется число 3
Число три это число гармонии и совершенства, которое используется во всех мировых культурах. Русскую землю охраняли в сказках три главных богатыря Илья Муромец, Добрыня Никитич и Алексей Попович. В былине об Илье Муромце к нему приходили три старца. Змей Горыныч имел три головы, у старика трое сыновей — два умные, один дурак. Даже царство, которое вынужден искать сказочный герой, носит название тридесятого, которое лежит также за тридевять земель. Иван Царевич ищет счастья в трех царствах — Медном, Серебряном и Золотом. Можно сказать, что число три появляется едва ли не во всех русских народных сказках, даже со звериными мотивами, как в известной сказке «Три медведя». Не обошел своей любовью тройку и родоначальник российской словесности Александр Пушкин, который с рассказами няни Арины Родионовны впитал дух русских сказок. Три девицы у поэта прядут под окном, Гвидон трижды посещает царство Салтана, старик со старухой жили у синего моря тридцать лет и три года, золотая рыбка соглашается исполнить для старика три желания. Работник Балда соглашается работать на попа всего за три щелчка.
Почему именно троица ?
Тройка популярна во всех странах и культурах, потому как это число выражает идею времени и пространства. Время делится на прошлое, настоящее и будущее, трёхмерное пространство заключается в длине, высоте и ширине. Человеческий возраст различается на молодость, зрелость и старость.
Даже сама Земля — третья планета от солнца. Христианская религия, принятая Русью, выражает бога через троицу — Отца, Сына и Святого Духа. Часть исследователей полагает, что популярность троицы пришла к нам именно из христианства.
Символическое значение числа 4
Еще одна цифра, часто встречающаяся в сказках, — это 4. Число ассоциируется с устойчивостью, мировым порядком. Встречается оно часто, например: столько существует сторон света,
4 мировые стихии, 4 времени года. Всего существует четыре периода человеческой жизни: детство, юность, зрелость, старость. Цифру 4 читатель встречает в сказке «Колобок», так как всего столько персонажей встретило главного героя на его пути. В произведении «Лиса, заяц и петух» ровно 4 раза звери пытались спасти зайца.
Пословицы и поговорки с числом 7
Семь – самое «путаное» число на свете. Семерка – число, которое используется, чтобы указать на что – то необычное, даже сверхъестественное. Число 7 – символ обновления. Большое значение числу семь придаёт христианская религия. «Бог создал мир за 7 дней», посвятив седьмой день отдыху. В глубокой древности это число долгое время считалось неопределённо большим количеством.
Семь раз отмерь, один раз отрежь.
Семеро одного не ждут.
Семь пятниц на неделе.
Тайна за семью печатями.
Семеро с ложкой, а один с сошкой.
У семи нянек дитя без глазу.
Семеро – не один, в обиду не дадим.
Лук от семи недуг.
Семь ворот, да все в огород.
Одним махом семерых убивахом.
Семеро одного не ждут.
Семи пядей во лбу.
Семь бед — один ответ.
Символическое значение числа 7
Сказки «Волк и семеро козлят» и «Дочь семилетка», семь цветов радуги, столько же чудес света, 7 дней недели — повсюду нас сопровождает таинственная и магическая цифра 7.
Если мы обратимся к нумерологии то обнаружим, что подобное число в сказках могло символизировать святость, разум, крепкое здоровье. Данная цифра означала победу мудрости над злом.
Пословицы и поговорки с числом 12
Очень почитается число двенадцать, «дюжина»:
12 месяцев в году,
12 знаков Зодиака,
12 делений на циферблатах часов,
сервизы на 12 персон.
В году двенадцать месяцев, и в каждом — свои ягоды.
Правда двенадцать цепей разорвет.
Одного воробья на двенадцать блюд не разложишь.
Символическое значение числа 12
Среди наиболее распространенных сказок, в которых упоминается это число, «Двенадцать месяцев».
Упоминается данное число также в сказках о Елене премудрой, Кощее бессмертном. Считалось, что это число позволяет заглянуть в глаза правде, позволяет человеку своими глазами, понять, что происходит и принять единственно правильное решение.
Пословицы и поговорки с числом 13
Тринадцать сулит одни неприятности. Оно простое и делится только на себя и единицу. Суеверия, связанные с числом 13, оказались наиболее устойчивыми и получили наибольшее распространение.
У наших предков – славян не было суеверий, связанных с числом 13.
Вашего брата по тринадцати на дюжину кладут,
да и то не берут.
Тринадцатый гость под стол.
Пословицы и поговорки с числом 100
100 — число, выражающее полное совершенство (10×10).
Эра делится на столетия.
Число 100 состоит из единицы и двух нулей.
Цифра 1 с языка чисел переводится как «энергия».Цифра 0 переводится как «созревание» или «засыпание» энергии.
Не имей сто рублей, а имей сто друзей.
Лучше один раз увидеть, чем сто раз услышать.
Одним махом сто побивахом, а прочих не считахом.
Сто голов — сто умов.
Трус умирает сто раз, а герой — один раз.
Одна весна на Родине лучше, чем сто весен на чужбине.
Для матери ребёнок до ста лет дитёнок.
В субботу в обед будет сто лет.
Верный друг лучше сотни слуг.
Заключение
Люди с древних времён вкладывали в числа определённый смысл. Всё это нашло отражение в устном народном творчестве, в том числе и в пословицах и поговорках.
Русская народная традиция тяготеет больше к слову, чем к числу. Тем не менее, она пронизана числовой символикой, проявляющейся в сказках. Присутствие чисел в ней наблюдается повсюду, и почти всегда они выступают как священные и глубоко символические.
Оказалось, что чаще всего в пословицах, поговорках и сказках встречаются числа: 1, 2, 3, 7.
Источники информации:
Александров Э., Левшин В. В лабиринте чисел. М.: Художественная литература, 2004
Аникин В.П. Русские народные пословицы, поговорки, загадки и детский фольклор. М.: Просвещение, 2004
Волина В.В. Пословицы, поговорки, ребусы. С.- Пб, Дидактика Плюс, 2009
Даль В.И. Пословицы русского народа, М.: Художественная литература, 2003
Пословицы, поговорки. http://www.poskart.ru/tsifry.html
Пословицы про счёт. http://posl.sc11tavda.edusite.ru/p3aa1.html
Числа и пословицы. http://gimnasy.tukalinsk.omskedu.ru/index.php/component/content/article/225.html
Картинки.
Магическое значение чисел в сказках. https://grimuar.ru/numerologia/znachenie-chisel-v-skazkah.html#h2_1
«Когда мы говорим о молодых ребятах и девчонках, для нас, действительно, было приятным откровением, что они готовы смотреть сложные лекции, готовы тратить на это большое количество времени. Мы, кажется, поняли очень важный ответ: им важна не просто сумма знаний, им важны глаза человека, личный пример. Люди, которые собрались в этом зале, все, кто представлен к номинации премии общества “Знание”, — это, в первую очередь, вдохновители, люди, которые воодушевляют, передавая частичку своего огня, блеск своих горящих глаз и свою искреннюю веру в то, что они делают», — отметил он.
Во время загрузки произошла ошибка.
Так, лучшим просветительским проектом стал конкурс «Большая перемена», который также победил в номинации «За лучшее просветительское мероприятие». В 2021 году в нем приняли участие 2,5 млн школьников и студентов колледжей. «Конкурс запустился одновременно с пандемией и смог ответить на массовый запрос подростков и детей быть полезными. Мир развивается такими темпами, что сегодня большинство подростков уже имеет рабочие, актуальные предпринимательские проекты, ребята очень увлечены научно-техническими разработками, развиваются творчески. И каждый должен получить возможность раскрыть свой потенциал. Сегодня большая перемена — это не просто конкурс, это огромная команда, настоящая семья, где важен талант каждого», — сказал на церемонии награждения генеральный директор АНО «Большая перемена» Валерий Моргуновский.
Лучшим просветителем года стал главный внештатный специалист сердечно-сосудистой хирургии Минздрава России, профессор хирургии Леонид Бокерия, он также стал победителем в номинации «Спорт и ЗОЖ».
Он до сих пор оперирует огромное число больных с врожденными и приобретенными пороками сердца и сердечных клапанов. «Я хочу вам всем пожелать крепкого здоровья, я хочу каждому, если здесь такие есть, кто этого не сделал, обязательно привиться, потому что эта зараза (коронавирус) ничего другого не признает, кроме прививки. Я хочу пожелать, чтобы те поколения людей, кто через пять, 10, 50 лет будут стоять на этом месте, были лучше, счастливее нас и более долговечней», — сказал Бокерия на сцене.
Юниорское движение Worldskills Russia стало победителем премии «Знание» за вклад в сфере «Достижения и гордость России».
«Через движение юниоры получают возможность раннего погружения в профессии по компетенциям Worldskills. Основными направлениями деятельности юниорского движения являются чемпионаты и финалы по стандартам Worldskills, общеразвивающая программа “Профильные техноотряды”, профориентационные фестивали профессий», — говорится на сайте премии.
Лучшим просветительским проектом в интернете был выбран лекторий «Достоевский» — бесплатная универсальная современная медиатека видео, аудио, подкастов, курсов и вебинаров. Лучшим просветителем в интернете стал Денис Прудник, ведущий популяризатор космонавтики в РФ, основатель проекта «Мы верим в космос». В исторической номинации среди проектов победила мультимедийная выставка-комикс «Александр Невский», которая состоит более чем из 140 видеопроекций разного формата, а лучшим просветителем в этой номинации стал антрополог Станислав Дробышевский.
В номинации «Просвещение по радио и ТВ» победу среди проектов одержал документальный фильм «Гибель империи. Российский урок» о событиях времен Февральской революции 1917 года, а среди просветителей в этой номинации победил доктор физико-математических наук Алексей Семихатов, который с 2014 года ведет программу «Вопрос науки» на телеканале «Наука». Лучшим документальным фильмом признана картина «Гагарин. Жизнь в хронике ТАСС». Фильм рассказывает подробности о том, как ТАСС освещал полет Гагарина, и раскрывает интересные и порой малоизвестные моменты из жизни космонавта через эксклюзивные фотографии, многие из которых никогда не публиковались.
В номинации «Культура и искусство» победу одержал проект «Сказки для и про особенных детей». Это социальные сказки, герои которых отличаются от своего окружения. Проект призван мотивировать особенных детей и их родителей верить в лучшее будущее, расти и развиваться. Среди просветителей победителем в этой номинации стал руководитель проекта SiberiaDOC Николай Бем, который занимается развитием авторского документального кино в Сибири.
В номинации «За активную просветительскую деятельность в школе» победил проект «Билет в будущее», посвященный ранней профессиональной ориентации учеников 6-11 классов.
Учителем-просветителем года признан Алексей Ермолин, автор методики осмысленного обучения и создания креативных презентаций «Смыслографика». В номинации «За активную просветительскую деятельность в вузе» жюри отдали победу проекту развития жестового языка «POжестI». Преподавателем-просветителем в этой номинации признан старший преподаватель кафедры физики высоких энергий и элементарных частиц Санкт-Петербургского государственного университета Антон Шейкин.
Обладателей призов зрительских симпатий объявлял генеральный директор общества «Знание» Максим Древаль. «Я очень рад, что так много талантливых, выдающихся людей вносят свой вклад в общее дело просвещения, мотивации и вдохновения молодежи. Я знаю, что в данной номинации более 10 тысяч человек отдали свои голоса за всех номинантов», — отметил он.
Приз зрительских симпатий получил проект «Что не найдешь в учебнике: вопросы и ответы». Это социально-исторический проект о героизме предков, неизвестных фактах истории России, которых еще нет в школьных учебниках. Лучшим просветителем зрители признали ученого-филолога, преподавателя Ивана Пыркова, который разработал фресковый метод преподавания литературы — предельная визуализация подаваемого материала, подача в сжатой, образной, яркой форме.
Премия «Знание» учреждена с целью признания заслуг российских просветителей, выявления значимых просветительских проектов и подтверждения высокого статуса просветителя в России. В 2021 году она проводится впервые, однако предполагается, что премия станет ежегодной.
В шорт-листы вошли 103 номинанта, после чего жюри определило лауреатов премии. В состав почетного жюри в том числе входят помощник президента РФ Андрей Фурсенко, гендиректор информационного агентства России ТАСС Сергей Михайлов, глава «Сбера» Герман Греф, министр культуры РФ Ольга Любимова, ректор МГУ имени М. В. Ломоносова Виктор Садовничий и ректор РАНХиГС Владимир Мау.
Лауреаты премии будут приглашены к сотрудничеству с обществом «Знание» и получат статус резидента «Центра знаний», который открывает доступ к широким возможностям мультимедийной инфраструктуры. Они также получат поддержку в продвижении своих проектов.
В награждении победителей принимали участие первый заместитель руководителя администрации президента РФ Сергей Кириенко, помощник президента Владимир Мединский, народные артисты России Константин Хабенский и Владимир Машков, гендиректор общества «Знание» Максим Древаль, руководитель Росмолодежи Ксения Разуваева и другие.
SLY_G
Вопрос Давида Гильберта о многочленах седьмой степени, долгое время считавшийся решённым, открыл исследователям новую сеть математических связей
Успех в математике достигается редко. Спросите хотя бы Бенсона Фарба.
«Проблема математики в том, что в 90% случаев вас ждёт неудача, и вам нужно быть человеком, умеющим это принимать», — сказал однажды Фарб за ужином с друзьями. Когда один из гостей, также математик, удивился тому, что Фарбу удаётся достигать успеха в целых 10% случаев, Фарб признал: «Нет, нет, я сильно преувеличил процент своих успехов».
Фарб, тополог из Чикагского университета, с радостью встретил последнюю свою неудачу – хотя, честно говоря, это не только его заслуга. Вопрос связан с задачей, парадоксальным образом одновременно решённой и нерешённой, открытой и закрытой.
Задача – это 13-я из 23 математических проблем, которые не были решены в начале XX века. Тогда немецкий математик Давид Гильберт составил этот список, который, по его мнению, определял будущее математики. Задача связана с решением полиномиальных уравнений седьмой степени. Полином – это последовательность членов уравнения, каждый из которых состоит из числового коэффициента и переменных, возведённых в степень; между собой члены связываются сложением и вычитанием. Седьмая степень означает самую большую экспоненту у всех переменных.
Математики уже научились ловко и быстро решать уравнения второго, третьего и в некоторых случаях, четвёртого порядка. В эти формулы – в том числе и в знакомую квадратичную формулу для второй степени – входят алгебраические операции, то есть арифметические действия и извлечение корней. Но чем больше экспонента, тем запутаннее уравнение, и решать его становится всё сложнее. 13-я проблема Гильберта – это вопрос, можно ли выразить решение уравнения седьмого порядка через набор сложений, вычитаний, умножений, делений и алгебраических функций от максимум двух переменных.

В 1900 году Дэвид Гильберт составил список из 23 важнейших открытых проблем.
Ответ: вероятно, нет. Однако для Фарба это не просто вопрос решения сложного алгебраического уравнения. Он сказал, что 13-я проблема – одна из самых фундаментальных проблем математики, поскольку она поднимает глубокие вопросы: насколько сложны полиномы, и как это измерить? «Целый слой современной математики был изобретён для того, чтобы лучше понимать корни полиномов», — сказал Фарб.
Эта проблема затянула его и математика Джесси Вольфсона из Калифорнийского университета в Ирвине в математическую кроличью нору, ходы которой они изучают до сих пор. Она также привлекла к их раскопкам Марка Кисина, специалиста по теории чисел из Гарварда и старого друга Фарба.
Фарб признал, что они пока не решили 13-ю проблему Гильберта, и даже не приблизились к решению. Однако они раскопали почти исчезнувшие математические стратегии, и изучили связи проблемы с различными областями знаний, включая комплексный анализ, топологию, теорию чисел, теорию представлений и алгебраическую геометрию. Они применили собственные подходы, в частности, объединив полиномы с геометрией и сузив диапазон возможных ответов на вопрос Гильберта. Также их работа предлагает способ классификации полиномов по метрикам сложности – аналог классов сложности, имеющих отношение к нерешённой задаче равенства классов P и NP.
«Они на самом деле смогли извлечь из интереса более интересную его версию» по сравнению с теми, что изучались ранее, сказал Дэниел Литт, математик из университета Джорджии. «Они показывают математическому сообществу множество естественных и интересных вопросов».
Открыли, закрыли и снова открыли
Многие математики уже считали проблему решённой. В конце 1950-х гениальный советский учёный Владимир Игоревич Арнольд и его наставник Андрей Николаевич Колмогоров опубликовали свои доказательства. Для большинства математиков работа Арнольда-Колмогорова закрыла этот вопрос. Даже в Википедии – не истине в последней инстанции, но довольно разумном посреднике в поисках знаний – до последнего времени задача была отмечена как решённая.

Владимир Арнольд и его наставник Андрей Колмогоров в 1950-х доказали один из вариантов 13-й проблемы Гильберта – но, возможно, Гильберта интересовал другой её вариант.
Однако пять лет назад Фарб наткнулся на несколько интригующих строчек в эссе за авторством Арнольда, где знаменитый математик размышляет над своей работой и карьерой. Фарб с удивлением узнал, что Арнольд описывает 13-ю проблему как открытую, и сорок лет пытался решить задачу, которую он вроде бы уже решил.
«Существуют научные работы, где просто повторяется тезис о решённости проблемы. Они явно не понимают самой проблемы», — сказал Фарб. В то время он работал вместе с Вольфсоном, бывшим тогда постдоком, над проектом в области топологии. Когда он поделился найденными в работе Арнольда сведениями, Вольфсон подключился к проекту. В 2017 году во время семинара, посвящённого 50-летию Фарба, Кисин услышал доклад Вольсфона и с удивлением понял, что их идеи, касающиеся полиномов, связаны с вопросами его работы по теории чисел. Он присоединился к их команде.
Причина путаницы с этой проблемой вскоре стала ясна: Колмогоров и Арнольд решили только один из её вариантов. В их решении фигурировали непрерывные функции – такие, у которых нет резких разрывов, или точек перегиба. Среди таких функций – знакомые операции вроде синуса, косинуса, экспоненты, а также более экзотические.
Однако не все исследователи согласны с тем, что Гильберта интересовали именно они. «Многие математики считают, что Гильберт имел в виду алгебраические, а не непрерывные функции», — сказал Зиновий Рейхштейн, математик из университета Британской Колумбии. Фарб и Вольфсон работают над проблемой, которую, как они считают, и хотел изучить Гильберт.
Фарб сказал, что 13-я проблема – это калейдоскоп. «Раскрываешь эту штуку – и чем больше изучаешь, тем больше направлений и идей она открывает, — сказал он. – Она приоткрывает дверь к целому массиву задач, показывает всю прекрасную паутину математики».
Корни проблемы
Математики игрались с полиномами с момента изобретения самой математики. На каменных табличках 3000-летней давности видно, как вавилонские математики использовали формулу для решения полиномов второго порядка. Это был клинописный предшественник той самой квадратичной формулы, которую сегодня учат на уроках математики. Формула показывает, как найти корни полинома – то есть, значения x, при которых выражение ax2+bx+c, полином второй степени, становится равным нулю.
Со временем математики, естественно, заинтересовались вопросом о том, существуют ли такие чёткие и ясные формулы для полиномов высших порядков. «Многотысячелетняя история этой проблемы заключается в том, чтобы прийти к чему-то такому же мощному, простому и эффективному», — сказал Вольфсон.
Чем выше степень полинома, тем более громоздкими они становятся. В книге 1545 года «Ars Magna» [«Великое искусство»] итальянский эрудит Джероламо Кардано опубликовал формулы для поиска корней полиномов третьей и четвёртой степеней.
Корни кубического полинома ax3+bx2+cx+d=0 можно найти по следующей формуле:
Формула для полинома четвёртой степени выглядит ещё хуже.
«С ростом степени растёт и сложность, вырисовывается гора сложностей», сказал Курт Макмаллен из Гарварда. «Как нам покорить эту гору?».
Итальянский математик Паоло Руффини в 1799 году утверждал, что полиномы 5-й и больших степеней нельзя решить при помощи арифметических операций и извлечения корней. В 1824 году это доказал норвежский математик Нильс Хенрик Абель. Иначе говоря, подобной формулы для полинома пятой степени не существует. К счастью, появились другие идеи, предлагавшие способы изучать полиномы высших степеней, которые можно упростить через подстановку. К примеру, в 1786 году шведский юрист Эрланд Бринг показал, что любое уравнение вида ax5+bx4+cx3+dx2+ex+f=0 можно переписать в виде px5+qx+1=0, где p и q – комплексные числа, величину которых определяют a, b, c, d, e и f. Этот факт открыл новые подходы к скрытым свойствам полиномов.
В XIX веке Уильям Роуэн Гамильтон продолжил работы Бринга и других. В числе прочего он показал, что для поиска корней полинома шестой степени понадобятся лишь обычные арифметические операции, квадратные и кубические корни и алгебраическая формула, зависящая только от двух переменных.
В 1975 году американский алгебраист Ричарт Брауэр из Гарварда ввёл идею «степени резольвенты», описывающую минимальное количество членов, необходимых для описания полинома некоторой степени. Менее чем через год после этого Арнольд и японский специалист по теории чисел Горо Шимура в другой работе ввели почти такое же определение.
В модели Брауэра, первой попытке систематизации правил таких подстановок, 13-я проблема Гильберта – это вопрос о том, возможно ли, чтобы у полиномов седьмой степени степень резольвенты была меньше 3. Позднее он выдвинул сходные гипотезы по поводу полиномов шестой и восьмой степеней.
Однако в основе всех этих вопросов лежит более общий: каково наименьшее количество параметров, необходимое для поиска корней любого полинома? До какого нижнего предела можно дойти?
Визуальное мышление
Естественный подход к этому вопросу – представить себе, как выглядят полиномы. Полином можно записать как функцию – к примеру, f(x)=x2−3x+1, — и построить её график. Тогда поиски корней сводятся к тому, что функция становится равной нулю там, где её кривая пересекает ось х.
Чем выше степень полинома, тем сложнее его график. Функции третьего порядка с тремя переменными выдают гладкие но перекрученные поверхности в трёх измерениях. Зная, в какие места этих поверхностей смотреть, математики могут многое узнать о лежащей в их основе полиномиальной структуре.
В результате в попытках понять полиномы задействуется множество методов из алгебраической геометрии и топологии – разделов математики, фокусирующихся на том, что происходит с фигурами, когда они деформируются, сжимаются, растягиваются или ещё как-то изменяются без разрывов. «Анри Пуанкаре, по сути, изобрёл топологию, и чётко сказал, что сделал это, чтобы понять алгебраические функции, — сказал Фарб. – В то время люди с трудом изучали эти фундаментальные связи».
Сам Гильберт раскрыл особенно интересную связь, применив геометрию к этой проблеме. К тому времени, как он составил свой список проблем в 1900-м году, у математиков уже был большой набор трюков, позволявших понижать степени полиномов, но они всё равно не могли продвинуться дальше. Однако в 1927 году Гильберт описал новый трюк. Начал он с определения всех возможных способов упростить полиномы девятой степени, и нашёл среди них семейство особых кубических поверхностей.
Гильберт уже знал, что на каждой гладкой кубической поверхности – замысловатой фигуре, описываемой полиномом третьей степени – содержится ровно 27 прямых, вне зависимости от того, насколько перекрученной она выглядит. Эти прямые сдвигаются с изменением коэффициентов полиномов. Он понял, что зная положение одной из них, можно упростить полином девятой степени и найти его корни. Формуле требовалось всего четыре параметра – в современных терминах это значило, что степень резольвенты не превышает 4.
«Потрясающее озарение Гильберта состояло в том, что это чудо геометрии, происходящее из совершенно другого мира, можно было использовать, чтобы уменьшить степень резольвенты до 4», — сказал Фарб.
Движение к паутине связей
Когда Кисин помогал Фарбу и Вольфсону разбираться в задаче, они поняли, что общепринятое мнение о решённости 13-й проблемы Гильберта убило весь интерес в геометрическом подходе к степени резольвенты. В январе 2020 года Вольфсон опубликовал работу, оживившую этот подход. Она расширила геометрическое обращение Гильберта с полиномами девятой степени до более общей теории.
Гильберт сконцентрировался на кубических поверхностях для поисков решения полиномов девятой степени, содержавшего всего одну переменную. Но что насчёт полиномов более высоких степеней? Чтобы решить эту задачу сходным образом, подумал Вольфсон, можно заменить кубическую поверхность некоей «гиперповерхностью» высшего порядка, сформированной этими полиномами высших степеней со множеством переменных. Геометрия подобных поверхностей изучена не так хорошо, но за последние несколько десятилетий математики доказали, что в некоторых случаях на них всегда можно найти прямые.
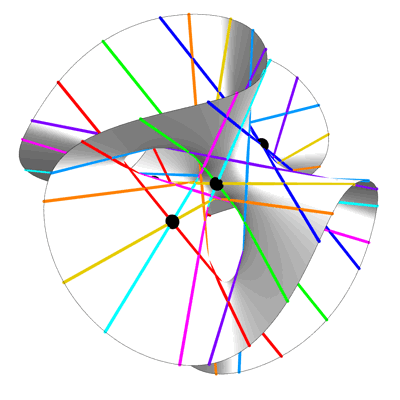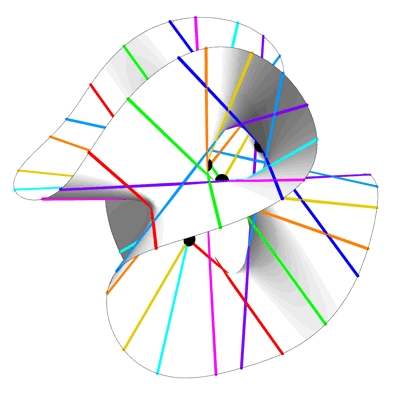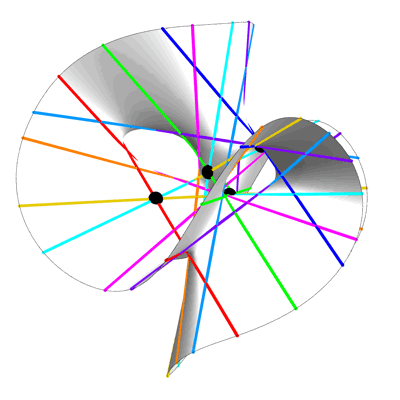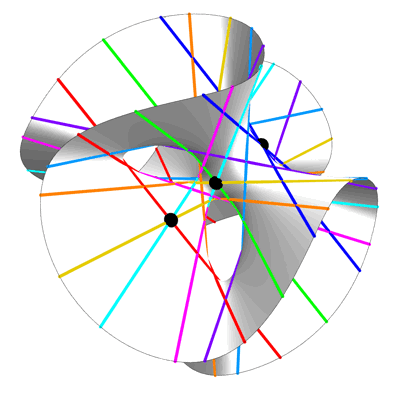
На любой гладкой кубической поверхности, неважно, насколько она перекручена или свёрнута, можно найти ровно 27 прямых линий. Гильберт использовал этот геометрический факт для создания формулы корней полинома девятой степени. Джесси Вольфсон развил эту идею далее, используя прямые на «гиперповерхностях» высших степеней для создания формул для более сложных полиномов.
Идею Гильберта использовать прямые на кубической поверхности можно развить до прямых, находящихся на этих «гиперповерхностях» высших степеней. Вольфсон использовал этот метод для нахождения новых, более простых формул для полиномов определённых степеней. Получается, что даже если представить себе полином 100-й степени у вас не получится, вы можете найти его корни, «просто» найдя плоскость на многомерной кубической гиперповерхности (в данном случае она будет иметь 47 измерений).
При помощи этого нового метода Вольфсон подтвердил найденную Гильбертом величину степени резольвенты для полиномов девятой степени. А для полиномов некоторых других степеней – в особенности, степеней выше 9 – его метод сужает диапазон возможных значений степени резольвенты.
Так что это не прямая атака на 13-ю проблему Гильберта, а подход к полиномам в целом. «Они нашли некие смежные вопросы и смогли достичь прогресса в них, надеясь, что это прольёт свет на оригинальный вопрос», сказал Макмаллен. И их работа указывает новые пути работы с этими математическими конструкциями.
Общая теория степени резольвенты также показывает, что гипотезы Гильберта касательно уравнений шестого, седьмого и восьмого порядка эквивалентны другим задачам, известным в, казалось бы, не связанных с полиномами областях математики. Степень резольвенты, по словам Фарба, предлагает способ выстроить эти проблемы по алгебраической сложности, а не группировать их по классам сложности.
И хотя теорию породила 13-я проблема Гильберта, математики не уверены, что она способна решить открытый вопрос по поводу полиномов седьмой степени. Она касается гигантских неизученных математических масштабов в невообразимых измерениях, но при меньших значениях степеней сталкивается с непреодолимыми препятствиями, и не в состоянии определить для них степени резольвенты.
Для Макмаллена отсутствие продвижения – несмотря на намёки на прогресс – интересно само по себе. Из этого следует, что в задаче таятся секреты, которые современная математика просто неспособна объять. «Мы не смогли подступиться к этой фундаментальной проблеме – это означает, что мы не заходили в какие-то тёмные области», — сказал он.
«Для её решения потребуются совершенно новые идеи», — сказал Рейхштейн, разработавший собственную идею по упрощению полиномов, концепцию, которую он называет «основным измерением». «Предугадать, откуда они появятся, невозможно».
Но троица не отступается. «Я не собираюсь сдаваться, — сказал Фарб. – Эта задача определённо стала моим белым китом. Она заставляет меня не останавливаться в этой паутине связей, и окружающей её математике».
ВВЕДЕНИЕ
Наше знакомство с числами началось с раннего возраста. Но встречаемся с числами мы не только на уроках математики, но и на уроках литературы.
При изучении русского фольклора, я заметила, что в пословицах и поговорках очень часто употребляются числа. Почему числа нашли свое отражение в русских пословицах и поговорках? Какова их роль в устном народном творчестве? Какое число самое «любимое» у русского народа?
На эти вопросы очень хотелось получить ответ.
Пословицы и поговорки прочно ложатся в память, их запоминание облегчается разными созвучиями, рифмами. Они кратки, в них нет лишних слов, каждое слово весомо, содержательно и точно. Яркую и точную характеристику пословицам дал сам народ: «Пословица недаром молвится», «Пословица правду всем говорит».
Цель работы: Изучить использование чисел в пословицах и поговорках и продемонстрировать важность числа как способа ярко и образно украсить повествование.
Методы исследования : Изучение русского народного творчества: пословиц, поговорок. Работа на поисковых и специализированных по тематике Интернет сайтах, со сборниками русских народных пословиц и поговорок. Анкетирование одноклассников.
Результатом работы является:
1. Осознание автором важности чисел в русском народном творчестве.
2. Приобретение практического опыта в освоении Интернет технологий, систематизации полученных знаний и создании презентаций с использованием программно — компьютерных средств.
Объект исследования
Пословицы и поговорки, содержащие числа.
Предмет исследования числа, содержащиеся в поговорках и пословицах
Моя работа имеет практическую значимость, потому что материалы исследования могут быть использованы для подготовки к уроку
Исторические сведения
Пословицы – краткие народные изречения с назидательным содержанием, народные афоризмы. В пословице есть второй смысл, это аллегория. Например, пословица: Чем дальше в лес, тем больше дров – может быть понята в прямом смысле. А может быть применена и к учёбе: чем больше узнаёшь, тем больше открывается нового и интересного.
У пословицы есть родная сестра – поговорка. Они похожи друг на друга. Поговорки – краткие устойчивые выражения, не составляющие, в отличие от пословиц, законченных высказываний. «Семь пятниц на неделе» – эта поговорка используется как часть суждения о тех, кто отступает от слова, меняет решение.
Таким образом, пословица – законченное предложение, а поговорка – часть предложения, часть суждения, без вывода, без заключения.
Отличие поговорки от пословицы сам народ видит в том, что поговорка – украшение речи – цветок, тогда как пословица – суждение полное, завершённое, зрелое – ягодка: «Поговорка – цветок, пословица – ягодка».
Веками создавал народ мудрые изречения – пословицы и поговорки. В них из поколения в поколение передавались главные мысли о жизни.
Самый большой сборник «Пословицы русского народа» Владимира Ивановича Даля, в котором более 30 000 пословиц и поговорок, содержит 178 разрядов по разным темам: Родина и дом, дружба, слово и учение, труд и мастерство, семья и воспитание, хвастовство, смелость, честь и человеческое достоинство, наружность.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 1.
Единица – изобретение математиков, она нужна для счета, и в магии чисел ее не существует. В древних текстах слово «один» употребляется нечасто и означает нечто неделимое, целостное, такое, как Бог, Космос, Вселенная. Если есть в Единице, какой — то магический смысл, то это смысл единого и целого. А в некоторых пословицах единица означает что — то очень малое, незначительное.
Один в поле не воин.
Один в море не рыбак.
Семь бед — один ответ.
Один за всех и все за одного.
Два медведя в одной берлоге не уживутся.
Семь раз отмерь, один раз отрежь.
За двумя зайцами погонишься — ни одного не поймаешь.
Лучше один раз увидеть, чем сто раз услышать.
Семеро одного не ждут.
В страду одна забота – не стояла бы работа.
От великого до смешного – один шаг.
Одна голова – хорошо, а две лучше.
Один дурак пятерых умных ссорит.
Одна голова – два языка.
Одна ласточка весны не делает.
Одна мучка, да разные ручки.
Правда одна, а на всех людей хватает.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 2.
Двойка – это символ разделения целого на части, символ отдельности человека от мира, природы и других людей. Это знак сравнения одного с другим. А еще Двойка – символ взаимоотношений и взаимодействий человека с тем, что его окружает.
Старый друг лучше новых двух.
Два медведя в одной берлоге не уживутся.
За двумя зайцами погонишься — ни одного не поймаешь.
Два сапога – пара.
Одна голова – хорошо, а две лучше.
Скупой платит дважды.
Убить двух зайцев.
Двум смертям не бывать, а одной не миновать.
Лентяй да шалопай – два родных брата.
Из двух зол выбирай меньшее.
За битого двух небитых дают.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 3.
Число три носит магический характер. Время мы делим на настоящее, прошедшее и будущее. Из глубокой древности до нас дошли поверья о том, что Земля держалась на трёх китах. Число три у многих народов священное. В Библии упоминается самое известное число три — это Троица, которая представляет Бога в трёх личностях: Бог — отец, Бог — сын и Святой дух.
Заблудиться в трёх соснах.
Бог любит троицу.
У мужика в августе три заботы: и косить, и пахать, и сеять.
Не узнавай друга в три дня – узнавай в три года.
Обещанного три года ждут.
От горшка три вершка.
Наврал с три короба.
Три волосинки в 6 рядов уложены.
Три волоска – и все густые.
Плакать в три ручья.
Согнуться в три погибели.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 4.
Число 4 в математике «Дважды два — четыре» — первое, что у большинства людей ассоциируется с понятием таблицы умножения. В образовании в России 4(четвёрка) — отметка , означающая «хорошо». Время каждый 4 — й год — високосный.
Без четырёх углов изба не рубится.
Конь о четырёх ногах, да и тот спотыкается.
Жить в четырёх стенах.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 5.
У человека и большинства высших животных 5 пальцев на одной конечности. В Олимпийском движении 5 разноцветных колец, символизирующих Европу, Азию, Африку, Америку и Австралию (в Антарктиде нет спорта и олимпийского движения).
Пятое колесо в телеге.
Знать как свои пять пальцев.
Рассказывать с пятого на десятое.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 6.
Известно, что в народе число 6 ассоциируется с нечистой силой. Поэтому в устном народном творчестве: пословицах, поговорках шестерка не упоминается.
Шестое чувство.
Шесть дней работай, седьмой – отдыхай.
Шесть дён лайся, седьмой – кайся.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 7.
Число 7 – символ обновления. Через 7 месяцев прорезываются зубы у младенца, в 7 лет обновляются зубы у ребёнка.
Большое значение числу семь придаёт христианская религия. «Бог создал мир за 7 дней», посвятив седьмой день отдыху. На Руси применялось в колдовстве и заклинаниях, лечили больных приёмами многократного повторения «святой» семёрки. «Сделай настой из семи трав на семи водах, пей семь дней по семь ложек».
Психологи установили, что один взгляд человека в состоянии охватить точное число предметов, если их не более шести. «Семь» – это уже «много». Видимо поэтому так много пословиц с числом 7 в значении «много». В глубокой древности это число долгое время считалось неопределённо большим количеством.
Семь раз отмерь, один раз отрежь.
Семеро одного не ждут.
Семь пятниц на неделе.
Тайна за семью печатями.
Семеро с ложкой, а один с сошкой.
Семь бед – один ответ.
У семи нянек дитя без глазу.
Семеро – не один, в обиду не дадим.
Лук от семи недуг.
Семь ворот, да все в огород.
За семью морями.
Семь пядей во лбу.
За семь вёрст киселя хлебать.
Семь вёрст до небес и всё лесом.
Семь топоров вместе лежат, а две прялки врозь.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 8.
Весна да осень – на дню погод восемь.
Восьмое чудо света.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 9.
За тридевять земель, в тридевятом царстве.
Девятый вал.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 10.
В тридевятом царстве, в тридесятом государстве.
Не трусливого десятка.
Рассказывать с пятого на десятое.
Девять человек — все равно, что десяток.
Одно дерево срубишь — десять посади.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ДРУГИЕ ЧИСЛА.
Не имей сто рублей, а имей сто друзей.
Лучше один раз увидеть, чем сто раз услышать.
Опять двадцать пять.
Весь материал – смотрите документ.