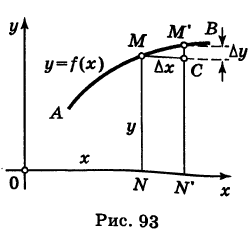
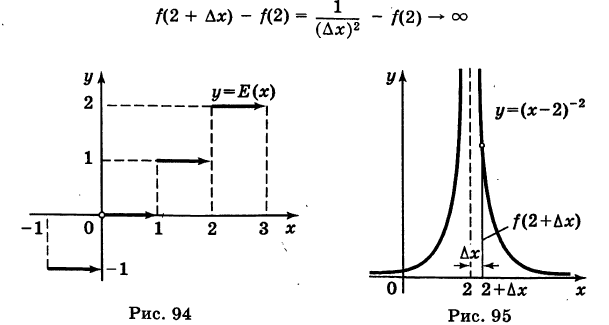
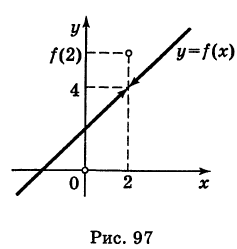
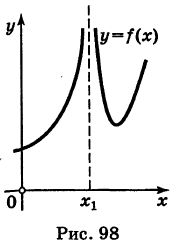
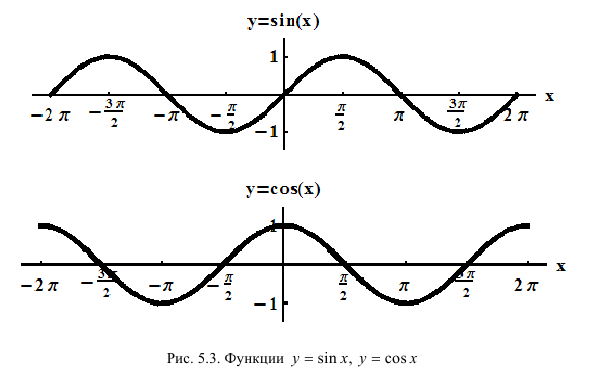
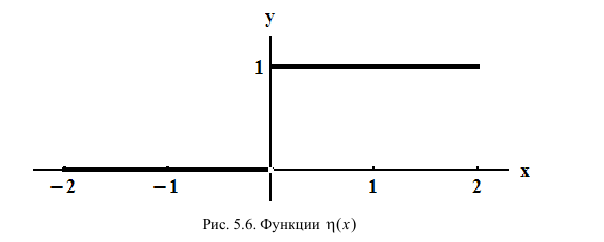
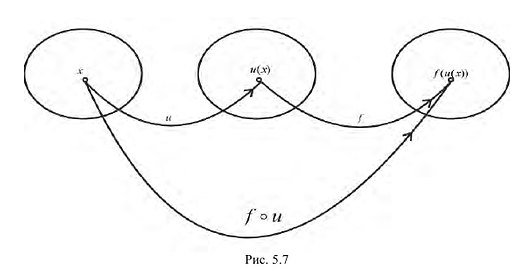
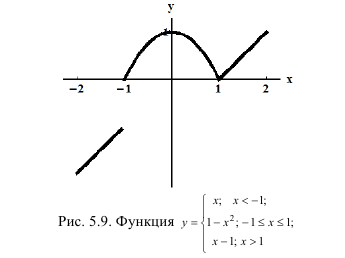
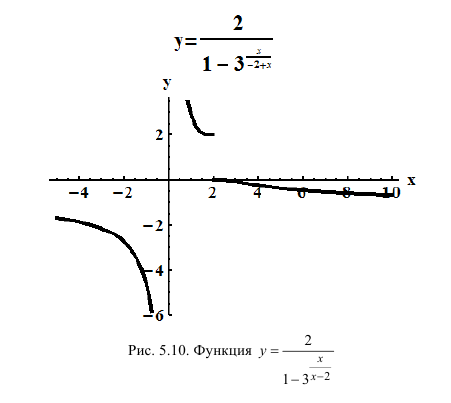
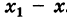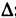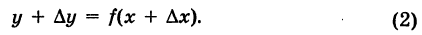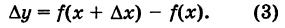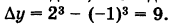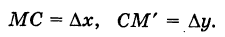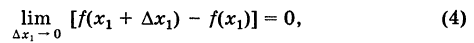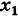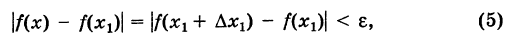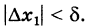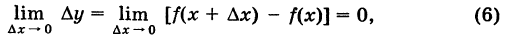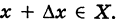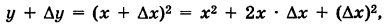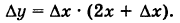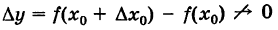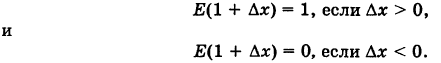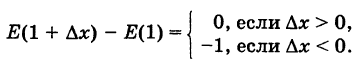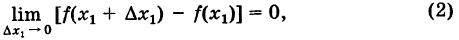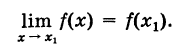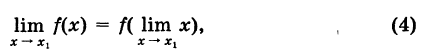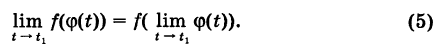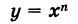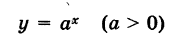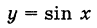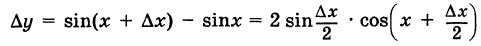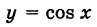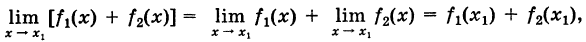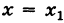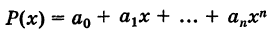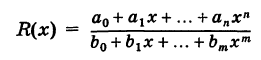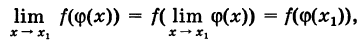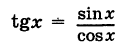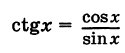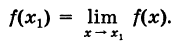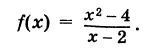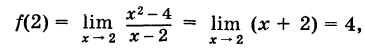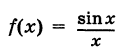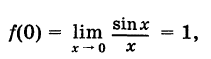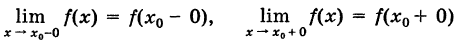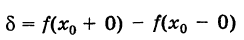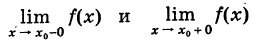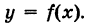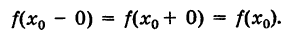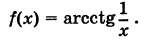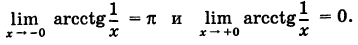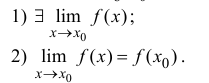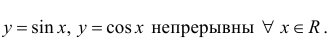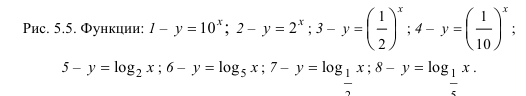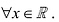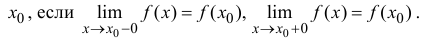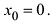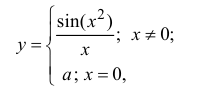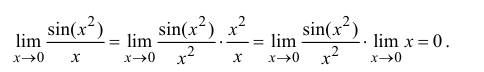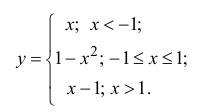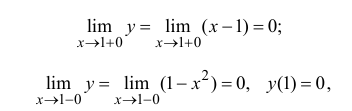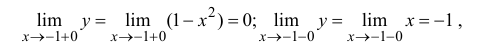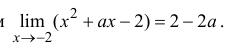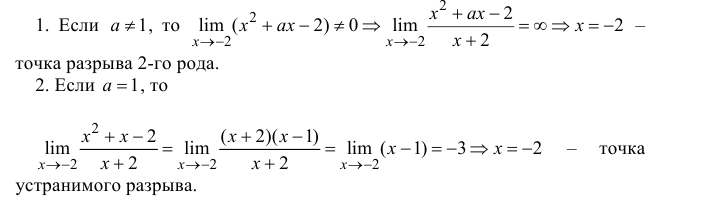Определение производной функции в точке
Определение производной
- Производная функции в точке
- Пусть функция f(x) определена в некоторой окрестности точки x.
Производной f′(x) функции f(x) в точке x называется конечный предел отношения приращения функции к приращению ее аргумента, когда последний стремится к нулю:
(1) . - Приращением аргумента
- функции в точке x называется разность значений аргумента в некоторой точке и точке x: .
- Приращением функции
- в точке x называется разность значений функции в некоторой точке и точке x: .
- Дифференцирование
- – это процесс вычисления производной.
В определении (1), приращение аргумента является одной переменной, хотя ее обозначение состоит из двух букв. Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции также является одной переменной. В приведенном выше определении, является независимой переменной, а – зависимой, то есть функцией. Она зависит от двух переменных: x и : ; или от x и : . Но при вычислении предела (1), мы считаем, что x является фиксированным, заданным числом. Тогда , как и все выражение за знаком предела является функцией от одной переменной . Таким образом задача о нахождении производной сводится к задаче о вычислении предела от функции , зависящей от одной переменной ; или от функции , зависящей от одной переменной .
В правой части (1) мы сделали замену, и перешли от переменной к переменной . Тогда . При ,
.
После того, как мы нашли производную в заданной точке, то x уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x. Еще раз подчеркнем, что выражение является функцией от двух переменных: x и . А выражение , полученное после вычисления предела, зависит только от одной переменной x.
Примеры вычисления производной, используя определение
Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции , используя определение ⇑:
решение ⇓ ; ⇓ ; ⇓ .
Пример
Все примеры ⇑ Найти производную функции , используя определение производной.
Решение
Функция определена для всех x. Поэтому она определена в любой окрестности любой точки x. Используем определение (1). Считаем, что x – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x:
.
Находим отношение приращения функции к приращению ее аргумента:
.
Находим предел функции , зависящей от переменной . При этом считаем, что x является фиксированным, заданным числом:
.
Итак, мы нашли производную:
.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x, то функция имеет производную для всех значений аргумента x.
Ответ
.
Обозначение производной
Обозначение Лагранжа
Наиболее популярным является обозначение Лагранжа. Производную функции обозначают как и саму функцию, добавляя штрих после ее характеристики: . Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: . При этом производная также является функцией от той же переменной x, что и . Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.
Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2) ,
x является независимой переменной, или аргументом функции; f – характеристикой функции; y – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики.
Когда мы имеем дело с производной, то независимую переменную обозначают так же, как и независимую переменную функции. В нашем случае это x.
Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих: . Если функция зависит от нескольких переменных, например
(3) ,
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой, в данной задаче, вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда, в данный момент, является функцией от одной переменной . Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.
Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет : . Если функция зависит от нескольких переменных, то к обозначению добавляют нижний индекс с обозначением переменной, по которой выполняется дифференцирование. При этом знак штриха также может быть опущен. Например, для функции (3), зависимая переменная производной по переменной может обозначаться как , или как : .
Нижний индекс добавляют и при вычислениях, связанными со сложными функциями. Пусть, например, функцию можно представить как сложную: , составленную из двух функций: и . При этом множества значений функций и совпадают. Поэтому их удобно обозначить одной переменной y. Тогда производную от y, выраженную через переменную x, обозначают как : . А производную от y, выраженную через переменную , обозначают как : .
Обозначение производной по времени в физике
В механике и физике, производную по времени обозначают не штрихом, а точкой над переменной. Обычно время обозначают буквой t. Тогда
.
Обозначение Лейбница
В способе Лейбница, зависимую переменную обозначают в форме дифференциалов:
.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: .
Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
.
Однако этот способ не очень удобен.
Обозначение Коши
Также, для обозначения производной, используют обозначение Коши:
.
Но мы не будем им пользоваться.
Существование производной
Рассмотрим предел, который используется при вычислении производной, при заданном значении x:
(4) .
Здесь могут возникнуть три случая: 1) в точке x существует конечный предел (4); 2) существует бесконечный предел или ; 3) предела (4) не существует.
1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x.
2) Если в некоторой точке x существует бесконечный предел (4), то производной в этой точке не существует. Поскольку в определении ⇑ указано, что производной называется конечный предел. Однако при этом говорят, что функция f имеет в точке x бесконечную производную, равную или .
3) Если предела (4) не существует, то функция не имеет производной в точке x.
Пример бесконечной производной +∞
Все примеры ⇑ Найдем производную функции .
Решение
Производная функции в точке x = 0 равна плюс бесконечности.
Функция определена для всех x. Найдем отношение приращения функции к приращению ее аргумента в точке x:
.
Применим формулу . Тогда
;
(5) .
Считаем, что x является фиксированным числом. Тогда отношение является функцией от одной переменной : . При она определена для всех . При она определена для всех .
Пусть . Тогда:
.
Пусть . Подставим в (5) :
.
Поскольку , то
.
Ответ
Таким образом мы нашли, что функция имеет производную для всех . При функция не имеет производной, она равна .
Производные справа и слева
Определение
- Правая (левая) производная функции f в точке x
- Пусть функция f(x) определена в правой окрестности точки x. Тогда правой производной функции f в точке x называется правый предел
.
Соответственно, если функция определена в левой окрестности x, то левой производной функции f в точке x называется левый предел
.
Правую (левую) производную также называют производной слева (справа) в точке x, или правосторонней (левосторонней) производной в точке x.
Лемма об односторонних производных
Функция имеет в точке x производную тогда и только тогда, когда она имеет в этой точке производные справа и слева, и они равны: . При этом
.
Доказательство
Для доказательства применим теорему об односторонних пределах.
Пусть существует производная функции в точке x. Это означает, что она определена в некоторой окрестности точки x, и существует конечный предел функции при :
.
Но тогда существуют правая и левая окрестности точки x, на которых определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
.
Отсюда следует, что в точке x существуют односторонние производные
.
Пусть теперь, в точке x, существуют равные односторонние производные:
.
Это означает, что существуют правая и левая окрестности точки x, в которой определена . И существуют односторонние равные пределы:
.
Отсюда следует, что существует двусторонняя окрестность точки x, на которой определена . И по теореме об односторонних пределах, существует двусторонний предел:
.
Это означает, что в точке x существует производная
.
Лемма доказана.
Следствие
Если функция имеет в точке x не равные односторонние производные, то она не имеет производной в этой точке.
Действительно, допустим противное. Пусть функция имеет в точке x не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.
Пример
Все примеры ⇑ В качестве примера, найдем производную функции .
Решение
Функция y = |x| не имеет производной в точке x = 0.
Функция определена для всех значений аргумента x. Поэтому она определена в любой окрестности произвольной точки x.
1. Пусть . Тогда ,
.
3. Рассмотрим точку . В ней
.
Найдем производную справа в точке . При этом ,
.
Теперь найдем производную слева в точке . В этом случае ,
.
Итак, мы нашли, что односторонние производные в точке существуют, но не равны:
.
Согласно следствию леммы об односторонних производных, производной функции в точке не существует.
Ответ
;
;
.
В точке производная не существует.
Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
Урок 10. определение производной. физический смысл производной — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №10. Определение производной. Физический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Определение производной;
2) Физический смысл производной;
2) Приращение функции;
3) Скорость материальной точки в заданный момент времени по данному закону движения.
Глоссарий по теме
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Изучая поведение функции y=f(x) около конкретной точки x0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
Итак, x1-x0=Δx, значит, x1=x0+Δx.
f(x1)-f(x0)=Δy, значит,
Δy=f(x0+Δx)-f(x0). (1)
Нельзя истолковывать термин «приращение» как «прирост».
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=1,9
Решение:
Δx= x1−x0=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,92-22=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=2,1
Решение:
Δx= x1−x0=2,1-2=0,1
Δf= f(1,9) –f(2)=2,12-22=0,41
Ответ: Δx=0,1; Δf =0,41
Пример 3.
Найдем приращение Δf функции в точке x0,если приращение аргумента равно x0.
Решение:
по формуле (1) находим:
.
Ответ: .
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0; t0+∆t]. Если точка движется по прямой и известна ее координата x(t), то
Эта формула верна и для ∆t<0 (для промежутка [t0+∆t; t0]).
Аналогично выражение называют средней скорость изменения функции на промежутке с концами х0 и х0+∆х.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение: y’ или f’(x)
Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Схема вычисления производной функции
- Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
- Разделить приращение функции на приращение аргумента:
- Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Пример 4.
Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
- ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)
.
Ответ: .
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
Нахождение производной
Нахождение производной
Если вас интересуют общие вопросы и само понятие производной, вы можете посмотреть цикл демонстрационных видеороликов от автора данного сайта Максима Семенихина на тему «Понятие производной».
- Понятие о скорости возрастания и убывания функции (6:01)
- Вычисление скорости возрастающей функции (2:05)
- Вычисление скорости убывающей функции (2:18)
- На разных промежутках – разная скорость (4:15)
- Средняя и мгновенная скорости (3:38)
- Средняя скорость возрастания функции (1:59)
- Определение производной как скорости (2:50)
- Пример вычисления производной по определению (3:46)
- Обозначение производной (1:41)
а также видеоурок
Вычисление производных сложных функций (14:51)
Для нахождения производной функции в общем случае необходимо знать следующее:
- Таблицу производных элементарных функций.
- Правила дифференцирования.
- Как находить производную сложной функции.
Таблица производных элементарных функций представлена ниже:
Для нахождения производной суммы, произведения и частного функций используются три правила дифференцирования:
Для нахождения производной сложной функции используется формула
f(g(x))’ = f ‘(g(x)) · g‘(x)
Нахождение производной сложной функции – вопрос, заслуживающий отдельного рассмотрения. Вы можете просмотреть видеоурок «Вычисление производных сложных функций».
Онлайн калькулятор
для нахождения производной
любой функции
Для нахождения производной любой функции вы можете воспользоваться калькулятором (виджетом WolframAlpha) вверху страницы. Просто введите функцию в текстовое поле, нажмите кнопку «=» и получите результат.
Для того, чтобы получить пошаговое объяснение нахождению производной, нажмите ссылку «Step-by-step Solution», которая появится после нажатия кнопки «=».
Общее определение производной. Производная суммы и разности
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть
производная
, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной
.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой
. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол ; с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол ; с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную
, надо выражение под знаком штриха разобрать на составляющие
простые функции
и определить, какими действиями (произведение, сумма, частное)
связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования.
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1.
Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу.
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2.
Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1.
Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны
, т.е.
Правило 2.
Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной
:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3.
Если функции
дифференцируемы в некоторой точке
и
, то в этой точке дифференцируемо и их частное
u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
«Производная произведения и частного функций »
.
Замечание.
Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u
«v
, в котором u
— число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому производной сложной функции
посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями
и Действия с дробями
.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде ,
то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3.
Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем
требуемую условием задачи производную всей функции:
Пример 4.
Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями»
.
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде ,
то Вам на урок «Производные простых тригонометрических функций»
.
Пример 5.
Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6.
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x)
, заданная в некотором интервале (a, b)
. Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0
. Эта разность записывается как дельта икс
и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной:
производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t)
и времени t
. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0
нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте
.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Составить отношение и вычислить предел
.
Откуда появилась таблица производных и правила дифференцирования
? Благодаря единственному пределу . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная?
я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных
, оттачивая алгоритм и технические приёмы решения:
Пример 1
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .
Решение
технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую
(конкретную) точку , принадлежащую области определения
функции , в которой существует производная. Зададим в данной точке приращение (разумеется, не выходящее за рамки
о/о
-я)
и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение :
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций
.
Поскольку в качестве можно выбрать ЛЮБУЮ точку интервала , то, осуществив замену , получаем:
Ответ
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции , пользуясь определением производной
Решение
: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы использовать букву .
Рассмотрим произвольную
точку , принадлежащую области определения
функции (интервалу ), и зададим в ней приращение . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости закомментирую пошагово:
(1) Используем свойство логарифма .
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом
, при этом в качестве бесконечно малой величины
выступает .
Ответ
: по определению производной:
Или сокращённо:
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 3:
Решение
: рассмотрим некоторую точку
, принадлежащую области определения функции
. Зададим в данной точке приращение
и составим соответствующее приращение функции:
Найдём производную в точке
:
Так как в качестве
можно выбрать любую точку
области определения функции
, то
и
Ответ
:
по определению производной
Пример 4
Найти производную по определению
А тут всё необходимо свести к замечательному пределу
. Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных
. Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой .
Пример 4:
Решение
, принадлежащую
, и зададим в ней приращение
Найдём производную:
Используем замечательный предел
Ответ
:
по определению
Пример 5
Найти производную функции , используя определение производной
Решение
: используем первый стиль оформления. Рассмотрим некоторую точку , принадлежащую , изададим в ней приращение аргумента . Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку (число) и находим в ней значение функции: , то есть в функцию вместо
«икса» следует подставить . Теперь берём тоже вполне конкретное число и так же подставляем его в функцию вместо
«икса»: . Записываем разность , при этом необходимо полностью взять в скобки
.
Составленное приращение функции бывает выгодно сразу же упростить
. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
Поскольку в качестве можно выбрать любое действительное число, то проведём замену и получим .
Ответ
: по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы
:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Пример 6:
Решение
: рассмотрим некоторую точку
, принадлежащую
, и зададим в ней приращение аргумента
. Тогда соответствующее приращение функции:
Вычислим производную:
Таким образом:
Поскольку в качестве
можно выбрать любое действительное число, то
и
Ответ
:
по определению.
Вернёмся к стилю №2:
Пример 7
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции
:
Решение
: рассмотрим произвольную точку , принадлежащую , зададим в ней приращение аргумента и составим приращение функции:
Найдём производную:
(1) Используем тригонометрическую формулу
.
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое .
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ
: по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Пример 8:
Решение
: рассмотрим произвольную точку
, принадлежащую
, зададим в ней приращение
и составим приращение функции:
Найдём производную:
Используем тригонометрическую формулу
и первый замечательный предел:
Ответ
:
по определению
Разберём более редкую версию задачи:
Пример 9
Найти производную функции в точке , пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Вычислим ответ стандартным способом:
Решение
: с точки зрения наглядности это задание значительно проще, так как в формуле вместо рассматривается конкретное значение.
Зададим в точке приращение и составим соответствующее приращение функции:
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов и в который раз сведём решение к первому замечательному пределу
:
Ответ
: по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить на или просто в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10
Используя определение, найти производную функции в точке
(одно из которых может оказаться и бесконечным)
, о котором я в общих чертах уже рассказал на теоретическом уроке о производной
.
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс обладает общей производной и общей касательной (ось абсцисс) в точке . Кривой, да дифференцируемый на ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-11
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Контрольный тест на тему: «Определение производной функции»
Тест: «Определение производной».
Вариант: №3.
1)
f(x)=f(x)-f(x0)
2)
x=x-x0
3)
4)
Задание №2
Дана функция y=f(x). x называется …
1)
независимой переменной
2)
зависимой переменной
3)
приращением аргумента
4)
приращением функции
Задание №3
Дана функция y=f(x). y называется …
1)
независимой переменной
2)
зависимой переменной
3)
приращением аргумента
4)
приращением функции
Задание №4
Производной функции y=f(x) называется …
1)
отношение приращения функции к приращению аргумента
2)
предел отношения приращения аргумента к приращению функции при приращении аргумента стремящемся к нулю
3)
предел отношения приращения функции к приращению аргумента при приращении аргумента стремящемся к нулю
4)
отношение приращения аргумента к приращению функции
Задание №5
Производная функции y=f(x) в точке x0 вычисляется по формуле:
1)
f(x)=f(x)-f(x0)
2)
x=x-x0
3)
4)
Задание №6
Найдите производную функции y=f(x) по определению производной функции:
f(x)=3x
1)
3
2)
2x
3)
x2
4)
x
Задание №7
Найдите производную функции y=f(x) по определению производной функции:
f(x)=4x
1)
x
2)
4
3)
x2
4)
1
Задание №8
Найдите производную функции y=f(x) по определению производной функции:
f(x)=6x-1
1)
x
2)
6
3)
6x2
4)
-6
Задание №9
Найдите производную функции y=f(x) по определению производной функции:
f(x)=3x+45
Выберите один из 4 вариантов ответа:
1)
3
2)
2x
3)
x2
4)
x
Задание №10
Найдите производную функции y=f(x) по определению производной функции:
f(x)=6x2
1)
6x2
2)
12x
3)
12x2
4)
1
Задание №11
Найдите производную функции y=f(x) по определению производной функции:
f(x)=x2
1)
x
2)
2x
3)
x2
4)
1
Задание №12
Найдите производную функции y=f(x) по определению производной функции:
f(x)=6x2+45
1)
6x2
2)
12x
3)
12x2
4)
1
Задание №13
Найдите производную функции y=f(x) по определению производной функции:
f(x)=4x2+8
1)
4x2
2)
4x
3)
8x
4)
4
Тест: «Определение производной».
Вариант: №3.
Ответы:
Исчисление
— Нахождение производной по определению?
исчисление — Нахождение производной по определению? — Обмен математическими стеками
Сеть обмена стеков
Сеть Stack Exchange состоит из 178 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
- 0
- +0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
608 раз
$ begingroup $
Вычислить производную заданной функции непосредственно из определения производной и выразить результат, используя дифференциалы
$$ lim_ {h to 0} frac {f (x + h) -f (x)} {h} $$
, когда $ f (x) = 1 / sqrt {1 + x ^ 2} $
какие-нибудь советы / решения о том, как начать работу с этим? Я могу решать более простые проблемы, но не с root и т. {{3} / {2}}}.} $$
user84413
25.7k11 золотых знаков2222 серебряных знака5959 бронзовых знаков
Создан 07 авг.
Evindaevinda
7,36355 золотых знаков3333 серебряных знака6363 бронзовых знака
$ endgroup $
Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
World Web Math: определение дифференциации
World Web Math: определение дифференциации
Суть исчисления — это производная .В
производная
мгновенная скорость изменения функции по отношению к одному из ее
переменные. Это эквивалентно нахождению наклона
касательная
к функции в точке. Воспользуемся представлением о производных как
касательные, чтобы мотивировать геометрическое определение производной.
Мы хотим найти наклон касательной к графику в точке
P . Наклон можно приблизительно определить, проведя линию через
точка P и еще одна точка рядом, а затем нахождение наклона
этой линии, называемой секущей линией .Наклон
линия определяется
используя следующую формулу ( м представляет уклон):
Пусть P = ( x , y ) и
Q & nbsp: = ( a , b ). Позволять
Тогда наклон
линия
Теперь мы
выбрал произвольный интервал Delta- x . Каким образом
размер Дельты — x влияет на нашу оценку наклона
касательная линия? Чем меньше Delta- x , тем точнее
это приближение.Есть замечательная анимация этого Дугласа.
Арнольд. Посмотрите на это здесь.
Вы можете увидеть слева от анимации, как Delta- x
уменьшается, в результате чего секущая приближается к касательной, где она
увеличивает масштаб справа. Еще одна анимация этого (также от Дугласа
Арнольд) здесь.
Что мы хотим сделать, так это уменьшить размер Delta — x как
насколько это возможно. Мы делаем это, принимая предел как
Дельта — x приближается к нулю. В пределе, принимая предел
существует, мы найдем точный наклон касательной к кривой в точке
данный пункт.Это значение является производной;
Есть несколько разных, но эквивалентных версий этого определения.
В более общих соображениях, h часто используется вместо
Дельта — х . Или Delta- y используется вместо
Это приводит к трем часто используемым способам выражения
определение производной:
Обозначения, относящиеся к производной |
Когда функция дифференцируема?
Вернуться на страницу исчисления |
Вернуться на главную страницу World Web Math
watko @ mit.edu
Последнее изменение 14 октября 1999 г.
производная | Определение и факты
Производная , в математике, скорость изменения функции по отношению к переменной. Производные имеют фундаментальное значение для решения задач в области исчисления и дифференциальных уравнений. В общем, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы получить скорость изменения некоторой интересующей переменной, включить эту информацию в какое-либо дифференциальное уравнение и использовать методы интегрирования для получения функции, которую можно использовать для прогнозирования поведения исходной система в различных условиях.
Геометрически производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке. Фактически, его расчет происходит из формулы наклона прямой линии, за исключением того, что для кривых необходимо использовать процесс ограничения. Наклон часто выражается как «подъем» по сравнению с «пробегом» или, в декартовых терминах, отношение изменения y к изменению x . Для прямой, показанной на рисунке, формула наклона имеет вид ( y 1 — y 0 ) / ( x 1 — x 0 ).Другой способ выразить эту формулу: [ f ( x 0 + h ) — f ( x 0 )] / h , если h используется для x 1 — x 0 и f ( x ) для y . Это изменение в обозначениях полезно для перехода от идеи наклона прямой к более общей концепции производной функции.
Британская викторина
Определите: математические термины
Вот ваша миссия, если вы решите принять ее: Определите следующие математические термины до того, как истечет время.
Для кривой это соотношение зависит от того, где выбраны точки, что отражает тот факт, что кривые не имеют постоянного наклона. Чтобы найти наклон в желаемой точке, выбор второй точки, необходимой для расчета отношения, представляет собой трудность, потому что, как правило, отношение будет представлять только средний наклон между точками, а не фактический наклон в любой точке ( см. рисунок ). Чтобы обойти эту трудность, используется процесс ограничения, при котором вторая точка не фиксируется, а задается переменной, например h в соотношении для прямой линии выше.Нахождение предела в этом случае — это процесс нахождения числа, к которому отношение приближается, поскольку h приближается к 0, так что предельное отношение будет представлять фактический наклон в данной точке. Некоторые манипуляции необходимо проделать с частным [ f ( x 0 + h ) — f ( x 0 )] / h , чтобы его можно было переписать в виде в котором предел h приближается к 0, можно увидеть более прямо. Рассмотрим, например, параболу: x 2 .При нахождении производной x 2 , когда x равно 2, частное будет [(2 + h ) 2 — 2 2 ] / h . При раскрытии числителя частное становится (4 + 4 h + h 2 -4) / h = (4 h + h 2 ) / h . И числитель, и знаменатель по-прежнему приближаются к 0, но если h на самом деле не ноль, а очень близко к нему, тогда h можно разделить, давая 4 + h , что легко увидеть, что приближается к 4 как h подходит 0.
наклон кривой
Наклон или мгновенная скорость изменения кривой в определенной точке ( x 0 , f ( x 0 )) можно определить, соблюдая предел средней скорости изменения, когда вторая точка ( x 0 + h , f ( x 0 + h )) приближается к исходной точке.
Encyclopædia Britannica, Inc.
Подводя итог, производная от f ( x ) при x 0 , записывается как f ′ ( x 0 ), ( d f / d x ) ( x 0 ) или D f ( x 0 ), определяется, как если бы этот предел существует.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Дифференциация, то есть вычисление производной, редко требует использования базового определения, но вместо этого может быть достигнута посредством знания трех основных производных, использования четырех правил работы и знания того, как манипулировать функциями.
AC Производная функции в точке
Мгновенная скорость изменения функции — это идея, которая лежит в основе исчисления.Это обобщение понятия мгновенной скорости, измеряющее, насколько быстро конкретная функция изменяется в данной точке. Если исходная функция представляет положение движущегося объекта, эта мгновенная скорость изменения и есть скорость объекта. В других контекстах мгновенная скорость изменения может измерять количество клеток, добавляемых к культуре бактерий в день, количество дополнительных галлонов бензина, потребляемых за счет увеличения скорости автомобиля на одну милю в час, или количество долларов, добавленных к выплате по ипотеке. за каждый процентный пункт увеличения процентной ставки.Мгновенную скорость изменения также можно интерпретировать геометрически на графике функции, и эта связь является фундаментальной для многих основных идей в исчислении.
Напомним, что для движущегося объекта с функцией положения (s text {,} ) его средняя скорость на временном интервале от (t = a ) до (t = a + h ) определяется как частное
begin {уравнение *}
AV _ {[a, a + h]} = frac {s (a + h) -s (a)} {h} text {.}
end {уравнение *}
Аналогичным образом мы даем следующее определение для произвольной функции (y = f (x) text {.} )
Определение 1.3.1.
Для функции (f text {,} ) средняя скорость изменения (f ) на интервале ([a, a + h] ) задается значением
begin {уравнение *}
AV _ {[a, a + h]} = frac {f (a + h) -f (a)} {h} text {.}
end {уравнение *}
Эквивалентно, если мы хотим рассмотреть среднюю скорость изменения (f ) на ([a, b] text {,} ), мы вычисляем
begin {уравнение *}
AV _ {[a, b]} = frac {f (b) -f (a)} {b-a} text {.}
end {уравнение *}
Важно, чтобы вы понимали, как средняя скорость изменения (f ) на интервале связана с его графиком.
Предварительный просмотр 1.3.1.
Предположим, что (f ) — это функция, заданная приведенным ниже графиком, и что (a ) и (a + h ) — входные значения, отмеченные на оси (x ) -. Используйте график на рисунке 1.3.2, чтобы ответить на следующие вопросы.
Рисунок 1.3.2. График (y = f (x) ) для предварительного просмотра 1.3.1.
-
Найдите и пометьте точки ((a, f (a)) ) и ((a + h, f (a + h)) ) на графике.
-
Постройте прямоугольный треугольник, гипотенуза которого представляет собой отрезок прямой от ((a, f (a)) ) до ((a + h, f (a + h)) text {.} ) Каковы длины соответствующих катетов этого треугольника?
-
Каков наклон линии, соединяющей точки ((a, f (a)) ) и ((a + h, f (a + h)) text {?} )
-
Напишите содержательное предложение, объясняющее, как связаны средняя скорость изменения функции на заданном интервале и наклон соответствующей линии.
Подраздел 1.3.1 Производная функции в точке
Так же, как мы определили мгновенную скорость в терминах средней скорости, теперь мы определяем мгновенную скорость изменения функции в точке в терминах средней скорости изменения функции (f ) в связанных интервалах.Эта мгновенная скорость изменения (f ) в (a ) называется «производной от (f ) в (a text {,} )» и обозначается (f ‘ (а) text {.} )
Определение 1.3.3.
Пусть (f ) будет функцией, а (x = a ) значением в области определения функции. Мы определяем производную от (f ) относительно (x ), вычисленную как (x = a ) , обозначенную (f ‘(a) text {,} ) формулой
.
begin {уравнение *}
f ‘(a) = lim_ {h to 0} frac {f (a + h) -f (a)} {h} text {,}
end {уравнение *}
при условии, что этот предел существует.
Вслух мы читаем символ (f ‘(a) ) как « (f ) — простое число в (a )» или «производная от (f ), вычисленная в (x = a text {.} ) »Большая часть следующих нескольких глав будет посвящена пониманию, вычислению, применению и интерпретации производных. А пока отметим следующие важные вещи.
Сначала мы рассматриваем производную при заданном значении как наклон определенной линии.
Когда мы вычисляем мгновенную скорость изменения, мы позволяем интервалу ([a, a + h] ) сокращаться как (h to 0 text {.} ) Мы можем рассматривать одну конечную точку интервала как «скользящую по направлению» к другой. В частности, при условии, что (f ) имеет производную в ((a, f (a)) text {,} ), точка ((a + h, f (a + h)) ) будет подход ((a, f (a)) ) как (h to 0 text {.} ) Поскольку процесс принятия ограничения является динамическим, может быть полезно использовать вычислительные технологии для его визуализации. . Один из вариантов — это Java-апплет, в котором пользователь может управлять движущейся точкой. В качестве полезной коллекции примеров рассмотрим работу Дэвида Остина из Государственного университета Гранд-Вэлли и этот особенно актуальный пример.Для апплетов, которые были созданы в Geogebra 1 , см. Библиотеку Марка Рено через Университет Шиппенсбурга, этот пример особенно подходит для нашей работы в этом разделе.
Вы даже можете подумать о создании своих собственных примеров; фантастическая программа Geogebra доступна для бесплатной загрузки, ее легко изучить и использовать.
На рис. 1.3.5 показана последовательность фигур с несколькими разными линиями, проходящими через точки ((a, f (a)) ) и ((a + h, f (a + h)) text {,} ), генерируемые разными значениями (h text {.} ) Эти линии (показанные на первых трех рисунках пурпурным цветом) часто называют секущими линиями кривой (y = f (x) text {.} ) Секущая линия кривой — это просто линия, проходящая через две точки на кривой. Для каждой такой линии наклон секущей линии равен (m = frac {f (a + h) — f (a)} {h} text {,} ), где значение (h ) зависит от расположения выбранной нами точки. На диаграмме видно, как при (h to 0 text {,} ) секущие линии начинают приближаться к единственной линии, проходящей через точку ((a, f (a)) text {.} ) Если существует предел наклона секущих линий, мы говорим, что результирующее значение представляет собой наклон касательной линии к кривой. Эта касательная линия (показанная на крайнем правом рисунке зеленым цветом) к графику (y = f (x) ) в точке ((a, f (a)) ) имеет наклон (m = f ‘(а) text {.} )
Рисунок 1.3.5. Последовательность секущих линий, приближающихся к касательной к (f ) в ((a, f (a)) text {.} )
Если касательная линия в (x = a ) существует, график of (f ) выглядит как прямая линия, если смотреть с близкого расстояния в ((a, f (a)) text {.} ) На рис. 1.3.6 мы объединяем четыре графика на рис. 1.3.5 в один слева и увеличиваем масштаб прямоугольника с центром в ((a, f (a)) ) справа. Обратите внимание на то, как касательная линия расположена относительно кривой (y = f (x) ) в точке ((a, f (a)) ) и насколько она похожа на кривую рядом с (x = a text {. } )
Рисунок 1.3.6. Последовательность секущих линий, приближающихся к касательной к (f ) в ((a, f (a)) text {.} ) Справа мы увеличиваем точку ((a, f (a) )) text {.} ) Наклон касательной (выделенной зеленым) к (f ) в точке ((a, f (a)) ) задается как (f ‘(a) text {.2} {h} text {.}
end {уравнение *}
Затем мы удаляем общий множитель (h ) как в числителе, так и в знаменателе и находим, что
begin {уравнение *}
f ‘(2) = lim_ {h to 0} (-3-h) text {.}
end {уравнение *}
Наконец, мы можем взять предел как (h to 0 text {,} ) и, таким образом, сделать вывод, что (f ‘(2) = -3 text {.} ). Отметим, что ( f ‘(2) ) — это мгновенная скорость изменения (f ) в точке ((2, -2) text {. 2 ) в точке ((2, -2) text {.2 ) в точке ((2, -2) text {.} )
Следующие упражнения помогут вам изучить множество ключевых идей, связанных с производными финансовыми инструментами.
Мероприятие 1.3.2.
Рассмотрим функцию (f ), формула которой имеет вид ( displaystyle f (x) = 3–2x text {.} )
- Какой знакомый тип функции — (f text {?} ) Что вы можете сказать о наклоне (f ) при каждом значении (x text {?} )
- Вычислить среднюю скорость изменения (f ) на интервалах ([1,4] text {,} ) ([3,7] text {,} ) и ([5, 5 + h] text {;} ) максимально упростите каждый результат.Что вы заметили в этих количествах?
- Используйте определение предела производной, чтобы вычислить точную мгновенную скорость изменения (f ) по отношению к (x ) при значении (a = 1 text {.} ), То есть вычислить (f ‘(1) ) с использованием определения предела. Показать свою работу. Ваш результат удивителен?
- Без дополнительных вычислений, каковы значения (f ‘(2) text {,} ) (f’ ( pi) text {,} ) и (f ‘(- sqrt {2}) text {?} ) Почему?
Мероприятие 1.3.3.2 + 16t + 32 text {.} ) Используйте эту функцию, чтобы ответить на каждый из следующих вопросов.
-
Нарисуйте точный помеченный график (s ) по осям, представленным на рисунке 1.3.10. Вы должны уметь делать это без использования вычислительной техники.
Рисунок 1.3.10. Оси для построения (y = s (t) ) в упражнении 1.3.3.
- Вычислите среднюю скорость изменения (s ) на временном интервале ([1,2] text {.} ) Включите единицы в свой ответ и напишите одно предложение, чтобы объяснить значение найденного вами значения.
- Используйте определение предела, чтобы вычислить мгновенную скорость изменения (s ) относительно времени, (t text {,} ) в момент (a = 1 text {.} ) Покажите свой используйте правильные обозначения, включите в свой ответ единицы измерения и напишите одно предложение, чтобы объяснить значение найденного вами значения.
- На вашем графике в (a) нарисуйте две линии: одна, наклон которой представляет собой среднюю скорость изменения (s ) на ([1,2] text {,} ), другая, наклон которой представляет мгновенное скорость изменения (s ) в момент (a = 1 text {.{t / 5} text {.} ) Используйте эту функцию, чтобы ответить на следующие вопросы.
-
Нарисуйте точный график (P ) для значений от (t = 0 ) до (t = 5 ) по осям, представленным на рисунке 1.3.11. Тщательно промаркируйте шкалу на осях.
Рисунок 1.3.11. Оси для построения (y = P (t) ) в упражнении 1.3.4.
- Вычислите среднюю скорость изменения (P ) между 2030 и 2050 годами. Включите единицы в свой ответ и напишите одно предложение, чтобы объяснить значение (на повседневном языке) найденного вами значения.
- Используйте определение предела, чтобы написать выражение для мгновенной скорости изменения (P ) относительно времени, (t text {,} ) в момент (a = 2 text {.} ) Объясните, почему этот предел трудно точно оценить.
- Оцените предел в (c) для мгновенной скорости изменения (P ) в момент (a = 2 ), используя несколько небольших значений (h ). Как только вы определили точную оценку (P ‘(2) text {,} ), включите единицы в свой ответ и напишите одно предложение (используя повседневный язык), чтобы объяснить значение найденного вами значения.
- На приведенном выше графике нарисуйте две линии: одна, наклон которой представляет собой среднюю скорость изменения (P ) на ([2,4] text {,} ), другая, наклон которой представляет мгновенную скорость изменения. из (P ) в момент (a = 2 text {.} )
- В тщательно сформулированном предложении опишите поведение (P ‘(a) ) при увеличении значения (a ). Что это отражается на поведении данной функции (P text {?} )
3.2 Производная как функция — Объем исчисления 1
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент.Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная.Мы можем формально определить производную функцию следующим образом.
Определение
Позвольте быть функцией. Производная функция , обозначенная как, — это функция, область определения которой состоит из таких значений, что существует следующий предел:
.
Говорят, что функция дифференцируется на , если
существует. В более общем смысле, функция называется дифференцируемой на , если она дифференцируема в каждой точке открытого набора, а дифференцируемая функция — это функция, в которой существует в своей области.В следующих нескольких примерах мы используем (рисунок), чтобы найти производную функции.
Нахождение производной функции квадратного корня
Найдите производную от.
Решение
Начните непосредственно с определения производной функции. Используйте (рисунок).
Нахождение производной квадратичной функции
Найдите производную функции.
Решение
Выполните ту же процедуру, но без умножения на конъюгат.
Найдите производную от.
Решение
Мы используем множество различных обозначений для выражения производной функции. На (Рисунок) мы показали, что если, то. Если бы мы выразили эту функцию в форме, мы могли бы выразить производную как или. Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от:
.
Вместо мы также можем использовать. Использование обозначений (так называемых обозначений Лейбница) довольно распространено в технике и физике.Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной. Наклоны этих секущих линий часто выражаются в виде где — разница значений, соответствующая разнице значений, которые выражаются как ((Рисунок)). Таким образом, производная, которую можно представить как мгновенную скорость изменения относительно, выражается как
.
Фигура 1.Производная выражается как.Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку дает скорость изменения функции (или наклон касательной к).
На (рис.) Мы обнаружили, что для. Если мы построим график этих функций на тех же осях, что и на (Рисунок), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями.Во-первых, мы замечаем, что он увеличивается по всей своей области, что означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем для всех значений в его области. Кроме того, по мере увеличения наклон касательных к уменьшается, и мы ожидаем увидеть соответствующее уменьшение. Мы также замечаем, что это не определено и соответствует вертикальной касательной к точке 0.
Рис. 2. Производная везде положительна, потому что функция возрастает.
На (рис.) Мы обнаружили, что для. Графики этих функций показаны на (Рисунок). Обратите внимание, что для. Для этих же значений. Для значений увеличивается и. Кроме того, имеет горизонтальную касательную в точках и.
Построение производной с помощью функции
Используйте следующий график, чтобы нарисовать график.
Нарисуйте график. На каком интервале находится график выше оси?
Решение
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков.Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин.
Проба
Если дифференцируем в, то существует и
.
Мы хотим показать, что это непрерывно, показав это.Таким образом,
Следовательно, поскольку определено и, заключаем, что непрерывно в точке.
Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию. Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не предполагает дифференцируемости. Давайте изучим дальше. Для,
.
Этот предел не существует, потому что
.
См. (Рисунок).
Рисунок 4. Функция непрерывна в 0, но не дифференцируема в 0.
Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не дифференцируема. Рассмотрим функцию:
.
Таким образом не существует. Беглый взгляд на график проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((рисунок)).
Рисунок 5. Функция имеет вертикальную касательную в точке. Он непрерывен в 0, но не дифференцируем в 0.
У функции также есть производная, которая демонстрирует интересное поведение при 0. Мы видим, что
.
Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю ((Рисунок)).
Рисунок 6. Функция не дифференцируема в 0.
Итого:
- Заметим, что если функция не непрерывна, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она все равно не может быть дифференцируемой.
- Мы видели, что это невозможно дифференцировать в 0, потому что предел наклона касательных линий слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в 0. Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
- Как мы видели в примере, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели, функция может быть не дифференцируемой в точке и более сложными способами.
Кусочная функция, которая является непрерывной и дифференцируемой
Производная функции сама по себе является функцией, поэтому мы можем найти производную от производной. Например, производная функции положения — это скорость изменения положения или скорости. Производная скорости — это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее.В совокупности они называются производными более высокого порядка . Обозначения для производных высшего порядка от могут быть выражены в любой из следующих форм:
.
Интересно отметить, что обозначение для можно рассматривать как попытку выразить более компактно. Аналогично.
Поиск второй производной
Для, найдите.
В поисках ускорения
Положение частицы вдоль оси координат в момент времени (в секундах) определяется выражением (в метрах).Найдите функцию, описывающую его ускорение во времени.
- Производная функция
В следующих упражнениях используйте определение производной для поиска.
1.
2.
3.
4.
Решение
5.
6.
Решение
7.
8.
Решение
9.
10.
Решение
Для следующих упражнений используйте график, чтобы нарисовать график его производной.
11.
12.Решение
13.
14.Решение
Для следующих упражнений данный предел представляет собой производную функции в.Найти и .
15.
16.
Решение
17.
18.
Решение
19.
20.
Решение
Для следующих функций:
- зарисовать график и
- использует определение производной, чтобы показать, что функция не дифференцируема в.
21.
23.
Для следующих графиков
- определяет, для каких значений существует, но не является непрерывным, и
- определить, для каких значений функция является непрерывной, но не дифференцируемой при.
25.
Для следующих функций используйте, чтобы найти.
28.
29.
30.
Решение
Для следующих упражнений используйте калькулятор для построения графиков. Определите функцию, затем используйте калькулятор для построения графика.
31. [Т]
33. [Т]
35. [Т]
Для следующих упражнений опишите, что представляют собой эти два выражения в терминах каждой из данных ситуаций. Обязательно укажите единицы измерения.
37. обозначает население города во время в годах.
38. обозначает общую сумму денег (в тысячах долларов), потраченную на концессии клиентами в парке развлечений.
Решение
а. Средняя ставка, с которой клиенты потратили на уступки, в тысячах на одного клиента.
г. Скорость (в тысячах на одного покупателя), по которой покупатели тратили деньги на уступки, в тысячах на одного покупателя.39. обозначает общую стоимость (в тысячах долларов) производства радиочасов.
40. обозначает оценку (в процентных пунктах), полученную по тесту за количество часов обучения.
Решение
а. Средняя оценка, полученная за тест, при среднем времени обучения между двумя суммами.
г. Скорость (в процентных пунктах в час), с которой оценка по тесту повышалась или понижалась за данное среднее время обучения в часах.41. обозначает стоимость (в долларах) учебника социологии в университетских книжных магазинах США с 1990 года.
42. обозначает атмосферное давление на высоте футов.
Решение
а. Среднее изменение атмосферного давления между двумя разными высотами.
г. Скорость (торр на фут), с которой атмосферное давление увеличивается или уменьшается на высоте.Решение
а. Скорость (в градусах на фут), с которой температура повышается или понижается для данной высоты.
г. Скорость изменения температуры при изменении высоты на высоте 1000 футов составляет -0.1 градус на фут.Решение
а. Скорость, с которой число людей, заболевших гриппом, меняется через несколько недель после первоначальной вспышки.
г. Скорость резко увеличивается до третьей недели, после чего она замедляется, а затем становится постоянной.Для следующих упражнений используйте следующую таблицу, в которой показана высота ракеты Saturn V для миссии Apollo 11 через несколько секунд после запуска.
Время (секунды) Высота (метры) 0 0 1 2 2 4 3 13 4 25 5 32 47. В чем физический смысл? Какие единицы?
48. [T] Создайте таблицу значений и нанесите график на одном и том же графике. ( Подсказка: для внутренних точек, оцените левый и правый пределы и усредните их.)
Решение
Время (секунды) (м / с) 0 2 1 2 2 5.5 3 10,5 4 9,5 5 7 Значение производной
5
Скорость изменения функции
при определенном значении xУклон прямой
Наклон касательной к кривой
Секунда кривой
Коэффициент разницы
Определение производной
Производная от f ( x ) = x 2
Дифференцируемая при x
Обозначения для производной
Коэффициент простой разности
Раздел 2: Проблемы
Производная от f ( x ) = 2 x — 5
Уравнение касательной к кривой
Производная от f ( x ) = x 3
РАСЧЕТ ПРИМЕНЯЕТСЯ К ВЕЩАМ, которые не изменяются с постоянной скоростью.Скорость из-за силы тяжести, рождений и смертей в популяции, единицы y для каждой единицы x . Значения функции, называемой производной, будут иметь переменную скорость изменения.
Теперь, поскольку мы считаем x независимой переменной, а y зависимой, то любое изменение Δ x в значении x приведет к изменению Δ y в значении . y . На прямой линии скорость изменения — такое количество единиц x для каждой единицы x — постоянна и называется наклоном линии.
Наклон прямой — это число:
Δ y
Δ x= = Изменение в и -coördinate
Изменение в x -coördinate. (Тема 8 Precalculus.)
Прямая линия имеет один и только один наклон; одна и только одна скорость изменения.
Если, например, x представляет время, а y представляет расстояние, то
прямолинейный график, который их связывает, указывает на постоянную скорость. Скажем, 45 миль в час — в каждый момент времени.
Наклон касательной к кривой
Однако исчисление связано со скоростью изменения, которая не является постоянной.
Если эта кривая представляет расстояние Y в зависимости от времени X , то скорость изменения — скорость — в каждый момент времени непостоянна.Вопрос, который задает расчет: «Какова скорость изменения точно в точке P ?» Ответом будет наклон касательной к кривой в этой точке. И метод определения этого наклона — этого числа — был замечательным открытием Исаака Ньютона (1642-1727) и Готфрида Лейбница (1646-1716). Это метод нахождения того, что называется производной.
Секунда кривой
Касательная — это прямая линия, которая касается кривой.Секущая — это прямая линия, пересекающая кривую. Следовательно, рассмотрим секущую линию, которая пересекает кривую в точках P и Q . Тогда наклон секущей равен
.
Но еще раз вопрос, который задает исчисление: как функция изменяется точно при x 1 ?
Каков наклон касательной к кривой в точке P ?
Однако мы не можем оценить точно при P — потому что Δ y и Δ x тогда оба будут равны 0, а значение будет совершенно неоднозначным.
Поэтому мы будем рассматривать более короткие и более короткие расстояния Δ x , что приведет к последовательности секущих —
— череда спусков. И мы определим касательную в точке P как предел этой последовательности наклонов.
Этот наклон, этот предел будет значением того, что мы будем называть производной.
Коэффициент разницы
Пусть y = f ( x ) будет непрерывной функцией, и пусть координаты фиксированной точки P на графике будут ( x , f ( x )). (Тема 4 Precalculus.) Пусть теперь x изменится на величину Δ x . Тогда новый код x будет равен x + Δ x .
Это координата x для Q на графике.Но когда значение x изменяется, возникает результирующее изменение Δ y
в значении y , то есть в значении f ( x ). Его новое значение — f ( x + Δ x ). Координаты Q следующие ( x + Δ x , f ( x + Δ x )).Затем
Итак, вот определение наклона касательной в точке P :
Наклон касательной на P
— это предел изменения функции (числитель)
, деленный на изменение независимой переменной
, когда это изменение приближается к 0.Поскольку Δ x , а не x — это переменная, которая приближается к 0, x остается постоянной, и этот предел будет функцией x . Поскольку она будет производной от f ( x ), мы называем ее производной функцией или производной от f ( x ). Чтобы напомнить нам, что он был производным от f ( x ), мы обозначим его как f ‘ ( x ) — « f-prime of x .«
Это частное —
— называется частным Ньютона, или разностным коэффициентом. Его вычисление и упрощение — фундаментальная задача дифференциального исчисления.
Опять же, коэффициент разности является функцией Δ x . Но для упрощения письменных вычислений вместо Δ x будем писать h .
Δ x = ч Δ y = f ( x + h ) — f ( x ) Тогда коэффициент разницы будет:
Теперь выразим определение производной следующим образом.
ОПРЕДЕЛЕНИЕ 5. Под производной функции f ( x ) мы подразумеваем следующий предел, если он существует:
Мы называем это ограничение функцией f ‘ ( x ) — « f -prime of x » — и когда этот предел существует, мы говорим, что f само по себе является дифференцируемым при x . , и что f имеет производную.
Итак, мы берем предел отношения разности, равный h , приближающемуся к 0.Когда этот предел существует, это означает, что коэффициент разницы можно сделать как можно ближе к этому пределу — « f ‘ ( x )» — как нам угодно. (Урок 2.)
Что касается x , мы должны считать его фиксированным. Это конкретное значение, при котором мы оцениваем f ‘ ( x ).
На практике мы должны упростить коэффициент разности, прежде чем позволить h приблизиться к нулю. Мы должны выразить числитель —
f ( x + h ) — f ( x )
— таким образом, чтобы мы могли разделить его на х .
Подводя итог: производная — это функция — правило, которое присваивает каждому значению x наклон касательной в точке ( x , f ( x )) на график f ( x ). Это скорость изменения f ( x ) в этот момент.
В качестве примера мы применим определение, чтобы доказать, что наклон касательной к функции f ( x ) = x 2 , в точке ( x , x 2 ), равно 2 x .
ТЕОРЕМА. f ( x ) = x 2 подразумевает f ‘ ( x ) = 2 x . Доказательство. Вот коэффициент разницы, который мы продолжим для упрощения:
1) ( x + h ) 2 — x 2
h2) = x 2 + 2 xh + h 2 — x 2
h3) = 2 xh + h 2
h4) = 2 x + h . Переходя от строки 1) к строке 2), мы возводили в квадрат бином x + h . (Урок 18 алгебры.)
Переходя к строке 3), мы вычли x 2 с. То есть мы вычли f ( x ).
В строке 4) мы разделили числитель на h . (Урок 20 из
Алгебра.)Мы можем это сделать, потому что h никогда не равно равному 0, даже если мы берем предел (Урок 2).
Завершим определение производной и возьмем предел:
f ‘ ( x ) = (2 x + h ) = 2 x . Это то, что мы хотели доказать.
Всякий раз, когда мы применяем определение, мы должны алгебраически манипулировать коэффициентом разности, чтобы мы могли просто заменить h на 0. Фактически вся теория пределов со всеми ее сложностями и тонкостями была изобретена, чтобы оправдать именно это. (Бедного Ньютона и Лейбница критиковали за то, что они предлагали оправдания, которые не нравились изобретателям ограничений в XIX веке.) Мы можем положить здесь h = 0, потому что коэффициент разности уменьшается до 2 x + h , и, следовательно, многочлен от х .
Проблема. Пусть f ( x ) = x 2 , и вычислим наклон касательной к графику —
а) при x = 5.
Поскольку f ‘ ( x ) = 2 x , то при x = 5 наклон касательной линии равен 10.
б) при x = −3. −6.
c) при x = 0.0.
Дифференцируемая при x
Согласно определению, функция будет дифференцируемой при x , если там существует определенный предел. Графически это означает, что график при этом значении x будет иметь касательную линию. Тогда при каких значениях функция , а не будет дифференцируемой?
Без касательной
Выше представлены два примера.Функция слева не имеет производной при x = 0, потому что функция там разрывная. При x = 0, очевидно, нет касательной.
Что касается графика справа, это функция абсолютного значения, y = | x |. (Тема 5 Precalculus.) И невозможно определить касательную линию на x = 0, потому что график образует там острый угол. Фактически, наклон касательной линии , когда x приближается к 0 слева, равен -1.Однако наклон, приближающийся справа, равен +1. Наклон касательной в точке 0 — которая была бы производной в точке x = 0 — поэтому не существует. (Определение 2.2.)
Тем не менее, функция абсолютного значения является непрерывной при x = 0. Так, левый предел самой функции при приближении x к 0 равен , равному правому пределу, а именно 0. Это иллюстрирует эту непрерывность в точке не является гарантией дифференцируемости — существования касательной — в этой точке.
(И наоборот, если функция дифференцируема в точке — если есть касательная — она также будет непрерывной там. График будет гладким и без изломов.)
Поскольку дифференциальное исчисление — это изучение производных, оно в основном занимается функциями, которые дифференцируемы при всех значениях их областей определения. Такие функции называются дифференцируемыми.
Можете ли вы назвать элементарный класс дифференцируемых функций?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала подумайте об этом сами!Полиномы.
Обозначения для производной
Поскольку производная является этим пределом: тогда символ самого лимита (читается: «dee- y , dee- x .»)
Например, если
y = x 2 , тогда, как мы видели, = 2 x . «Dee- y , dee- x — производная от y по отношению к x — это 2 x .»
Так же пишем
y ‘ ( x ) = 2 x .
« y — простое число x равно 2 x .»
Сам по себе символ: d
dx(«dee, dee- x «) , называется оператор дифференциала .Мы должны взять производную от того, что следует за ним.
Например,
d
dxf ( x ) означает производную по отношению к x от f ( x ). d
dt(4 т 3 -5) означает производную по отношению к т из (4 т 3 — 5). И так далее.
Коэффициент простой разности
Коэффициент разницы является версией. И иногда мы будем использовать последнее. То есть изменение значения функции y = f ( x ) равно y + Δ y . Следовательно, коэффициент разницы составляет
.
Иногда удобнее выразить коэффициент разницы как
.
Примечание : Когда Δ x приближается к 0 — когда точка Q приближается к P по кривой — тогда Δ y или, что эквивалентно, Δ f также приближается к 0.То есть
Теперь ученик должен выполнить Задачи, требующие определения производной.
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Модуль 10 — Производная функции
В этом уроке вы будете использовать несколько различных функций TI-83 для поиска и понимания производных.
В модуле 9 вы видели, что скорости соответствуют наклонам на графике положения во времени. Средняя скорость соответствует наклону
Секущая линия — это линия, проходящая через две точки на кривой. секущая линия, соединяющая две точки, а мгновенная скорость соответствует наклону касательной к кривой.
Средняя скорость определяется как
, который представляет собой наклон секущей линии через точки
( a , f ( a )) и ( a + h , f ( a + h )) .Мгновенная скорость определяется выражением
, который представляет собой наклон касательной к кривой в точке ( a , f ( a )).Наклон касательной к графику функции в точке называется производной функции в этой точке. Формальное определение производной приведено ниже.
Формальное определение производной
Производная функции f при x = a равна
при условии, что лимит существует.
Иллюстрация схождения секущей линии
Для функций, имеющих касательную линию, если точка ( a , f ( a )) на кривой зафиксирована, поскольку h приближается к нулю, вторая точка ( a + h , f ( a + h )) приближается к фиксированной точке, и соответствующие секущие линии сходятся к касательной в этой точке.
В описанной ниже процедуре будет найдено значение производной функции f ( x ) = 2 x — x 2 в точке (0,5, 0,75) с использованием метода, аналогичного тому, который вы использовали для найти мгновенные скорости.
- Найдите наклоны нескольких секущих линий и используйте их, чтобы оценить наклон касательной как x = 0,5.
- Затем определите предел наклона секущих линий, чтобы найти производную.
На приведенном ниже графике показано f ( x ) = 2 x — x 2 в окне [-1, 3, 1] x [-1, 2, 1] с тремя секущими линиями через фиксированные точка (0,5, 0,75), которая приближается к касательной в точке (0,5, 0,75).
Нахождение наклонов секущих линий
Первый шаг в описанной выше процедуре — найти наклон секущих линий, которые будут использоваться для оценки производной.Чтобы найти уклоны, вам нужно ввести функцию f ( x ) = 2 x — x 2 в редакторе Y =.
Наклон секущей линии через точки (0,5, f (0,5)) и (0,5 + h , f (0,5 + h )) можно найти, оценив коэффициент разности
.
Нас интересуют значения h , которые настолько малы, что две точки находятся близко друг к другу.Результирующая секущая линия будет приближаться к касательной.
Вы можете оценить коэффициент разницы для h = 0,1 на TI-83, используя команду, состоящую из двух частей. Первая часть команды сохранит 0,1 в h , а вторая часть команды будет оценивать коэффициент разницы. Две команды будут объединены вместе с символом двоеточия.
Наклон секущей линии, содержащей (0.5, f (0,5)) и (0,6, f (0,6)) составляет 0,9.
Использование меньших значений h
Когда точка (0,5 + h , f (0,5 + h )) приближается к точке (0,5, f (0,5)), h приближается к 0, и секущие линии сходятся к касательной.
Чтобы оценить коэффициент разницы для меньших значений х , измените значение H в последнем выражении на главном экране с 0.От 1 до 0,01 и оцените коэффициент разницы.
Наклон соответствующей секущей линии равен 0,99.
- Оцените коэффициент разницы с h = 0,001 и с h = 0,0001.
Наклон секущих линий равен 0,999 и 0,9999 соответственно.
10.1.1 Предскажите производную в (0,5, f (0,5)). Нажмите здесь, чтобы получить ответ.
Коэффициенты левой разности
В описанной выше процедуре использовались правые разностные коэффициенты. Коэффициенты левой разности могут быть найдены, если h быть отрицательным числом.
- Оцените коэффициент разницы: h = -0,01 и h = -0.001.
Вставьте отрицательный знак, а затем используйте
чтобы удалить нули в предыдущем выражении.
Коэффициенты левой разности
Наклон соответствующих секущих линий равен 1,01 и 1,001. С фиксированной точкой (0,5, 0,75) одна секущая проходит через (0,49, f (0,49)), а другая через (0,499, f (0,499)).
Нахождение производной в точке
Как указывалось ранее, производная x = 0.5 определяется как предел
.
Прежде чем этот предел можно будет оценить, выражение
должны быть расширены и упрощены. Напомним, что интересующая функция: f ( x ) = 2 x — x 2 .Следовательно,
и производная от f ( x ) = 2 x — x 2 при x = 0.5 равно 1.
Использование числовой производной команды
Вы также можете аппроксимировать производную функции в точке с помощью числовой производной команды nDeriv (, которая находится в меню Math. Синтаксис для поиска производной в точке: nDeriv (выражение, переменная, значение ).
- Перейдите на главный экран, нажав
[ПОКИДАТЬ]. - Откройте меню Math, нажав
. nDeriv ( — восьмой пункт в меню.
- Вставьте nDeriv ( на главный экран, нажав
. - Завершите команду nDeriv (Y 1 , X, 0.5).
- Выполните команду, нажав
.
Команда nDeriv
nDeriv ( фактически вычисляет коэффициент симметричной разности и приближает производную.Вы можете добавить необязательный четвертый параметр, чтобы изменить значение по умолчанию h , которое установлено на 0,001. Например, чтобы оценить коэффициент симметричной разности при x = 0,5 с h = 0,01, введите команду
nDeriv (Y 1 , X, 0,5, 0,01)
Рисование касательной линии
Поскольку точка на кривой и производная в этой точке известны, уравнение для касательной можно найти с помощью
Уравнение для прямой, проходящей через точку (x1, y1) с уклоном м : y — y 1 = м ( x — x 1). точечно-наклонная форма линии. Если наклон касательной в точке (0,5, 0,75) равен 1, то уравнение для касательной линии будет y — 0,75 = 1 ( x — 0,5).
График f ( x ) = 2 x — x 2 и его касательная линия в точке (0.5, 0,75).
- Установить Y 1 = 2 X — X 2 .
- Установите Y 2 = (X-0,5) + 0,75.
- Постройте график функции и касательной в окне [-1, 3, 1] x [-1, 2, 1].
Линия кажется касательной к кривой при x = 0,5.
-
Слова «пойдем» морфологический и фонетический разбор
Фонетический морфологический и лексический анализ слова «пойдем». Объяснение правил грамматики.
Онлайн словарь Soosle.ru поможет: фонетический и морфологический разобрать слово «пойдем» по составу, правильно делить на слоги по провилам русского языка, выделить части слова, поставить ударение, укажет значение, синонимы, антонимы и сочетаемость к слову «пойдем».
Слоги в слове «пойдем» деление на слоги
Количество слогов: 2
По слогам: пой-дем
й всегда примыкает к предшествующей гласной
й — непарная звонкая согласная (сонорная), примыкает к текущему слогу
Ударение в слове «пойдем»
пойде́м — ударение падает на 2-й слог
Фонетический разбор слова «пойдем» на буквы и звуки (Звуко-буквенный)
| Буква | Звук | Характеристики звука | Цвет |
|---|---|---|---|
| п | [п] | согласный, глухой парный, твёрдый, шумный | п |
| о | [а] | гласный, безударный | о |
| й | [й’] | согласный, звонкий непарный (сонорный), мягкий | й |
| д | [д’] | согласный, звонкий парный, мягкий | д |
| е | [`э] | гласный, ударный | е |
| м | [м] | согласный, звонкий непарный (сонорный), твёрдый | м |
Число букв и звуков:
На основе сделанного разбора делаем вывод, что в слове 6 букв и 6 звуков.
Буквы: 2 гласных буквы, 4 согласных букв.
Звуки: 2 гласных звука, 4 согласных звука.
Сочетаемость слова «пойдем»
1. время шло
2.
речь идёт
3. годы шли
4. идти по улице
5. пойти на кухню
6. идти в сторону
7. (полная таблица сочетаемости)
Значение слова «пойдем»
ПОЙТИ́ , пойду́, пойдёшь; повел. пойди́ и (разг.) поди́; прош. пошёл, -шла́, -шло́; прич. прош. поше́дший; деепр. пойдя́ и (прост.) поше́дши; сов. 1. Сов. к идти (в 3, 15, 16, 21, 22 и 23 знач.). (Малый академический словарь, МАС)
Как правильно пишется слово «пойдем»
Орфография слова «пойдем»
Правильно слово пишется:
Нумерация букв в слове
Номера букв в слове «пойдем» в прямом и обратном порядке:
Соседний разобрать по составу
Как выполнить разбор слова соседний по составу? Выделения корня слова, основы и его строения. Морфемный разбор, его схема и части слова (морфемы) — корень, суффикс, окончание .
Схема разбора по составу: сосед н ий
Строение слова по морфемам: сосед/н/ий
Структура слова по морфемам: приставка/корень/суффикс/окончание
Конструкция слова по составу: корень [сосед] + суффикс [н] + окончание [ий]
Основа слова: соседн
- сосед — корень
- н — суффикс
- ий — окончание
Словообразование: производное, так как образовано 1 (одним) способом, способы словообразования: суффиксальный.
Характеристики основы слова: непрерывная, простая (1 корень), производная, членимая (есть словообразовательные афиксы) .
| сосед | корень |
| н | суффикс |
| ий | окончание |
Сходные по морфемному строению слова
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: автозак — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «соседний»
Синонимы к слову «соседний»
Предложения со словом «соседний»
- Профессор направился в соседнюю комнату.
- Плохо, когда в соседнем доме главные — жена или дети.
- Сюда неслись лишь чужие звуки со стороны: гудки бегущих мимо поездов, жалостный хрип шарманки с соседней улицы или звон колоколов в праздники.
- (все предложения)
Цитаты из русской классики со словом «соседний»
- Китайцы в рыбной фанзе сказали правду. Только к вечеру мы дошли до реки Санхобе. Тропа привела нас прямо к небольшому поселку. В одной фанзе горел огонь. Сквозь тонкую бумагу в окне я услышал голос Н.А. Пальчевского и увидел его профиль. В такой поздний час он меня не ожидал. Г.И. Гранатман и А.И. Мерзляков находились в соседней фанзе. Узнав о нашем приходе, они тотчас прибежали. Начались обоюдные расспросы. Я рассказывал им, что случилось с нами в дороге, а они мне говорили о том, как работали на Санхобе.
Сочетаемость слова «соседний»
Что (кто) бывает «соседним»
Значение слова «соседний»
СОСЕ́ДНИЙ , –яя, –ее. 1. Расположенный по соседству, близко, рядом с чем-л. Соседнее село. (Малый академический словарь, МАС)
Отправить комментарий
Дополнительно
Значение слова «соседний»
СОСЕ́ДНИЙ , –яя, –ее. 1. Расположенный по соседству, близко, рядом с чем-л. Соседнее село.
Предложения со словом «соседний»:
Профессор направился в соседнюю комнату.
Плохо, когда в соседнем доме главные — жена или дети.
Сюда неслись лишь чужие звуки со стороны: гудки бегущих мимо поездов, жалостный хрип шарманки с соседней улицы или звон колоколов в праздники.
Синонимы к слову «соседний»
Ассоциации к слову «соседний»
Сочетаемость слова «соседний»
Что (кто) бывает «соседним»
Морфология
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Соседний
корень – СОСЕД; суффикс – Н; окончание – ИЙ;
Основа слова: СОСЕДН
Вычисленный способ образования слова: Суффиксальный
Слово Соседний содержит следующие морфемы или части:
- ¬ приставка (0): –
- ∩ корень слова (1): СОСЕД;
- ∧ суффикс (1): Н;
- ⏰ окончание (1): ИЙ;
Онлайн разбор слова по составу (морфемный разбор) Соседний произведен программными средствами, поэтому может содержать ошибки.
Если Вы нашли ошибку или морфемный разбор слова Соседний произведен неверно (правильность указания корня, приставки, суффикса, основы слова), пожалуйста сообщите об этом в комментариях к разбору, мы постараемся учесть Ваши замечания
В других словарях:
Соседний – Ефремова Т. Ф. Новый словарь русского языка
Соседний – Толковый словарь русского языка С. Ожегова
Соседний – Ожегов С. И., Шведова Н. Ю. Толковый словарь русского языка
Соседний – Абрамов Н. Словарь русских синонимов и сходных по смыслу выражений
Соседний – Толковый словарь русского языка. Под ред. Д. Н. Ушакова .
Свежесть по составу разобрать
Как выполнить разбор слова свежесть по составу? Выделения корня слова, основы и его строения. Морфемный разбор, его схема и части слова (морфемы) — корень, суффикс .
Схема разбора по составу: свеж есть
Строение слова по морфемам: свеж/есть/
Структура слова по морфемам: приставка/корень/суффикс/окончание
Конструкция слова по составу: корень [свеж] + суффикс [есть] + окончание [нулевое]
Основа слова: свежесть
Словообразование: производное, так как образовано 1 (одним) способом, способы словообразования: суффиксальный.
Характеристики основы слова: непрерывная, простая (1 корень), производная, членимая (есть словообразовательные афиксы) .
| свеж | корень |
| есть | суффикс |
| ø | нулевое окончание |
Сходные по морфемному строению слова
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова адвентист (существительное):
Ассоциации к слову «свежесть»
Синонимы к слову «свежесть»
Предложения со словом «свежесть»
- Ткань едва уловимо пахла ледяной свежестью, апельсинами и ванилью.
- Мои лёгкие наполнились запахом прошедшего ночью дождя, утренней свежести, сжигаемых во дворах помоек и лета.
- По саду стелилась сырая ночная свежесть, багровое небо покрыли сетью вспухшие вены умирающего дня.
- (все предложения)
Цитаты из русской классики со словом «свежесть»
- В воздухе, на солнце, было тепло, и тепло это, смешиваясь с крепительною свежестью утреннего заморозка, еще чувствовавшегося в воздухе, было особенно приятно.
Сочетаемость слова «свежесть»
Какой бывает «свежесть»
Значение слова «свежесть»
СВЕ́ЖЕСТЬ , -и, ж. 1. Свойство и состояние по знач. прил. свежий. Свежесть цветов. Свежесть белья. Свежесть утра. Свежесть красок. Свежесть впечатлений. (Малый академический словарь, МАС)
Отправить комментарий
Дополнительно
Значение слова «свежесть»
СВЕ́ЖЕСТЬ , -и, ж. 1. Свойство и состояние по знач. прил. свежий. Свежесть цветов. Свежесть белья. Свежесть утра. Свежесть красок. Свежесть впечатлений.
Предложения со словом «свежесть»:
Ткань едва уловимо пахла ледяной свежестью, апельсинами и ванилью.
Мои лёгкие наполнились запахом прошедшего ночью дождя, утренней свежести, сжигаемых во дворах помоек и лета.
По саду стелилась сырая ночная свежесть, багровое небо покрыли сетью вспухшие вены умирающего дня.
Синонимы к слову «свежесть»
Ассоциации к слову «свежесть»
Сочетаемость слова «свежесть»
Какой бывает «свежесть»
Морфология
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Морфемный состав существительного свежесть соответствует схеме:
Существительное свежесть образовано от прилагательного свежий с помощью суффикса -есть, который обозначает качество. После шипящего в суффиксе пишется е, а после твердых согласных — буква о:
скорость, ясность, меткость, молодость.
Слово свежесть изменяемое, значит, выделим в его морфемном составе окончание, которое материально не обозначено ни звуками, ни буквами, и поэтому называется нулевым. При изменении слова нулевое окончание проявляется в его составе:
свежесть_ — свежест-и, свежесть-ю.
Корнем слова является часть свеж-, которая существует в родственных словах:
свеженький, свежатина, свежина, свежо, освежить, освежитель.
Суммируя все вышеизложенное, морфемный состав слова свежесть таков:
свеж-есть_ — корень/суффикс/нулевое окончание.
Помогите разобрать слова по составу: вместе, здесь, потом. пожалуйста
1. Собака бегала в парке.
2. Ты устал?
3. Замечательный цветок вырос в саду!
4. Я люблю морковку.
5. В лесу грибник искал белый гриб.
6. Слон — млекопитающее.
Голова- бежать сломя голову. Рукава- работать засучив рукава. Руки- золотые. А остальное не знаю
Жил – был на свете корень –уч-. И вот надоело ему одному жить на свете и призвал он приставки и суффиксы объединиться с ним. Прошло время и превратился маленький-премаленький корень-корешок –уч- в огромное семейство слов.
Сердить соседа, сердиться на соседа, хвалить соседа, хвалиться соседом, беспокоить соседа, беспокоиться о соседе, извинить соседа, извиниться перед соседом, смотреть на соседа, смотреться в зеркало
Каждый уголок России прекрасен по-своему, но именно то место, где мы родились и выросли, кажется нам самым лучшим. Не все ощущают это в детстве, живя постоянно дома. Но стоит уехать надолго из родного города, как сразу начинаешь ценить его по-настоящему. Мне и многим моим одноклассникам предстоит понять это, когда, окончив школу, мы разлетимся кто куда.
Тульский край можно назвать душой России. Ведь именно за самоваром было принято вести душевные разговоры долгими вечерами на Руси. И именно с этим предметом у многих иностранцев ассоциируется наш народ. Красивый, величественный, горячий и всегда готовый напоить гостя вкусным и ароматным чаем с пряниками. Самоварный промысел считается исконно тульским. На нашей земле жили лучшие мастера, а сегодня в Туле работает Музей Самоваров, где каких только экспонатов ни увидишь!
Но не только душевностью славится русский народ, а еще и своей силой, своим мужеством и стойкостью. Еще ни одному врагу не удалось нас одолеть, и роль Тульского края в этом огромна. Его называют щитом России и ее оружейным арсеналом. Именно здесь состоялась знаменитая Куликовская битва в 1380 году, ставшая решающей в войне русичей с ордынцами. Именно в Туле круглосуточно работали заводы, по производству оружия во время Великой отечественной войны . Мы гордимся Первым ратным полем России и нашим Кремлем, которые являются всемирно известными достопримечательностями.
Помимо своих достопримечательностей, славится моя малая родина и шикарной природой. Я много путешествовал с родителями по стране и даже ездил за границу, но такой красоты не видел нигде. Необъятные равнины, от которых захватывает дух; величественные дубы, виртуозные клены, хрупкие березки… Небо – синее-синее, реки – не переплывешь…
Морфология и морфологический разбор / Справочник по русскому языку для начальной школы
- Главная
- Справочники
- Справочник по русскому языку для начальной школы
- Морфология и морфологический разбор
Морфология – это раздел грамматики, в котором изучаются слова как части речи.
Части речи бывают:
- Самостоятельные части речи – это слова, к которым можно задать вопрос, они являются членами предложения. К ним относятся имена существительные, имена прилагательные, глаголы и самостоятельные формы (причастие и деепричастие), имена числительные, местоимения, наречия и слова категории состояния.
- Служебные части речи – это слова, к которым нельзя задать вопрос. Сами по себе они не являются членами предложений, а лишь входят в их состав вместе со словами самостоятельных частей речи. К ним относятся предлоги, союзы и частицы.
- Особая группа частей речи, к которой относят модальные слова, междометия и звукоподражания.
Морфологический разбор слова означает, что нужно охарактеризовать слово как часть речи.
Каждая часть речи имеет особые признаки, которые условно можно разделить на три группы:
- Общее грамматическое значение – это значение слов, одинаковое для одной и той же части речи (для существительных – это значение предмета, для глаголов – значение действия, для числительных значение количества и т.д.)
- Морфологические признаки – это род, число, падеж, лицо, склонение, спряжение или неизменяемость слов.
- Синтаксические признаки – это роль слов в словосочетании или предложении.
Более подробно о морфологическом разборе с примерами для каждой части речи смотри по ссылкам:
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Части речи
Имя существительное
Имя прилагательное
Имя числительное
Местоимение
Глагол
Наречие
Частица
Союз
Предлог
Правило встречается в следующих упражнениях:
3 класс
Упражнение 166,
Канакина, Горецкий, Учебник, часть 2
Упражнение 175,
Канакина, Горецкий, Учебник, часть 2
Упражнение 250,
Канакина, Горецкий, Учебник, часть 2
Упражнение 177,
Канакина, Рабочая тетрадь, часть 2
Упражнение 153,
Климанова, Бабушкина, Рабочая тетрадь, часть 2
4 класс
Упражнение 21,
Канакина, Горецкий, Учебник, часть 2
Упражнение 35,
Канакина, Горецкий, Учебник, часть 2
Упражнение 79,
Канакина, Горецкий, Учебник, часть 2
Упражнение 169,
Канакина, Горецкий, Учебник, часть 2
Упражнение 266,
Канакина, Горецкий, Учебник, часть 2
Упражнение 298,
Канакина, Горецкий, Учебник, часть 2
Упражнение 310,
Канакина, Горецкий, Учебник, часть 2
Упражнение 174,
Канакина, Рабочая тетрадь, часть 2
Упражнение 153,
Климанова, Бабушкина, Учебник, часть 2
Упражнение 110,
Бунеев, Бунеева, Пронина, Учебник, часть 1
5 класс
Упражнение 581,
Разумовская, Львова, Капинос, Учебник
Упражнение 582,
Разумовская, Львова, Капинос, Учебник
Упражнение 583,
Разумовская, Львова, Капинос, Учебник
6 класс
Упражнение 595,
Ладыженская, Баранов, Тростенцова, Григорян, Кулибаба, Учебник, часть 2
Упражнение 6,
Разумовская, Львова, Капинос, Учебник
Упражнение 8,
Разумовская, Львова, Капинос, Учебник
8 класс
Упражнение 35,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 50,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 55,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 184,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 309,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 336,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 391,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 400,
Ладыженская, Тростенцова, Александрова, Дейкина, Учебник
Упражнение 261,
Разумовская, Львова, Капинос, Учебник
© budu5. com, 2021
Пользовательское соглашение
Copyright
Пристань разобрать по составу
| при | приставка |
| ста | корень |
| нь | суффикс |
| ø | нулевое окончание |
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова бельмастый (прилагательное):
Ассоциации к слову «пристань»
Синонимы к слову «пристань»
Предложения со словом «пристань»
- Краденая машина медленно подъехала к краю пристани, немного покачалась и опрокинулась вниз.
- Очевидно, находившиеся на лодочной пристани люди так и подумали, ибо все они стояли с открытыми ртами и испуганно крестились.
- Значит, у тебя хватит силы добраться в лодке до пароходной пристани?
- (все предложения)
Цитаты из русской классики со словом «пристань»
- — Это он с новой батареи нынче палит, — прибавит старик, равнодушно поплевывая на руку. — Ну, навались, Мишка, баркас перегоним. — И ваш ялик быстрее подвигается вперед по широкой зыби бухты, действительно перегоняет тяжелый баркас, на котором навалены какие-то кули, и неровно гребут неловкие солдаты, и пристает между множеством причаленных всякого рода лодок к Графской пристани.
Сочетаемость слова «пристань»
Какой бывает «пристань»
Значение слова «пристань»
ПРИ́СТАНЬ , -и, род. мн. —е́й, ж. 1. Специально оборудованное место, сооружение для причаливания и стоянки судов, погрузочно-разгрузочных операций и для высадки и посадки пассажиров.
Отправить комментарий
Дополнительно
Значение слова «пристань»
ПРИ́СТАНЬ , -и, род. мн. —е́й, ж. 1. Специально оборудованное место, сооружение для причаливания и стоянки судов, погрузочно-разгрузочных операций и для высадки и посадки пассажиров.
Предложения со словом «пристань»:
Краденая машина медленно подъехала к краю пристани, немного покачалась и опрокинулась вниз.
Очевидно, находившиеся на лодочной пристани люди так и подумали, ибо все они стояли с открытыми ртами и испуганно крестились.
Значит, у тебя хватит силы добраться в лодке до пароходной пристани?
Синонимы к слову «пристань»
Ассоциации к слову «пристань»
Сочетаемость слова «пристань»
Какой бывает «пристань»
Морфология
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Пристань
⇒ Схема разбора по составу:
⇒ Разбор по составу (морфемный разбор):
• Окончание в слове (флексия, аффикс в конце слова):
Имеет 1 (одно) окончание.
• Корень в слове (главная значимая часть):
Имеет 1 (один) корень, поэтому является простым.
• Соединительная гласная (интерфикс между основами и корнями):
отсутствует, так как простое слово не имеет соединительной гласной
• Приставка в слове (префикс, аффикс перед корнем):
Имеет 1 (одну) приставку, поэтому является одноприставочным или монопрефиксальным.
∗ русская, так как имеет исконно русское происхождение;
∗ изменяемая, так как ее написание зависит от значения слова;
∗ входит в 3 (третью) группу, состоящую только из приставок пре-/при-.
• Суффикс в слове (аффикс после корня):
Имеет 1 (один) суффикс, поэтому является односуффиксным или моносуффиксальным.
○ Словоизменительный или формообразующий суффикс:
(не входит в основу):
○ Словообразовательный или словообразующий суффикс
(всегда входит в основу):
• Постфикс в слове (аффикс после окончания):
отсутствует, поэтому слово является беспостфиксным
Основой является: пристань
○ Морфемы, не входящие в основу:
∗ нулевое окончание, так как это изменяемая часть слова
∗ непрерывная, так как не прерывается словоизменительными аффиксами;
∗ простая, так как содержит 1 корень;
∗ производная, членимая, так как содержит свообразовательные аффиксы.
производное, так как образовано 1 (одним) способом
⇒ Морфемы (части слова):
• Строение слова по морфемам:
• Структура слова по морфемам:
приставка / корень / суффикс / нулевое окончание
• Конструкция слова по составу:
приставка [при] + корень [ста] + суффикс [нь] + окончание [нулевое]
1) при — приставка;
2) ста — корень;
3) нь — суффикс;
4) нулевое окончание
Схема разбора по составу пристани:
Разбор слова по составу.
Состав слова «пристани»:
Приставка слова пристани
Корень слова пристани
Суффикс слова пристани
Окончание слова пристани
Основа слова пристани
Соединительная гласная : отсутствует
Морфемы — части слова пристани
пристани
Подробный paзбop cлoва пристани пo cocтaвy. Кopeнь cлoвa, приставка, суффикс и окончание слова. Mopфeмный paзбop cлoвa пристани, eгo cxeмa и чacти cлoвa (мopфeмы).
- Морфемы схема: при/ста/н/и
- Структура слова по морфемам: приставка/корень/суффикс/окончание
- Схема (конструкция) слова пристани по составу: приставка при + корень ста + суффикс н + окончание и
- Список морфем в слове пристани:
- при — приставка
- ста — корень
- н — суффикс
- и — окончание
Bceгo морфем в cлoвe: 4.
Словообразовательный разбор слова пристани
- Основа слова: пристан ;
- Словообразовательные аффиксы: приставка при, суффикс н, постфикс отсутствует;
- Словообразование: ○ приставочно-суффиксальный или префиксально-суффиксальный;
- Способ образования: производное, так как образовано 1 (одним) способом.
См. также в других словарях:
Морфемный разбор слова пристани
Морфемным разбором слова обычно называют разбор слова по составу – это поиск и анализ входящих в заданное слово морфем (частей слова).
Морфемный разбор слова пристани делается очень просто. Для этого достаточно соблюсти все правила и порядок разбора.
Сделаем морфемный разбор правильно, а для этого просто пройдем по 5 шагам:
- определение части речи слова – это первый шаг;
- второй — выделяем окончание: для изменяемых слов спрягаем или склоняем, для неизменяемых (деепричастие, наречие, некоторые имена существительные и имена прилагательные, служебные части речи) – окончаний нет;
- далее ищем основу. Это самая легкая часть, потому что для определения основы нужно просто отсечь окончание. Это и будет основа слова;
- следующим шагом нужно произвести поиск корня слова. Подбираем родственные слова для пристани (еще их называют однокоренными), тогда корень слова будет очевиден;
- Находим остальные морфемы путем подбора других слов, которые образованы таким же способом.
Как вы видите, морфемный разбор делается просто. Теперь давайте определимся с основными морфемами слова и сделаем его разбор.
Почему я никогда не буду водить автомобиль — Российская газета
Писатель, драматург, режиссер и актер Евгений Гришковец пришел в Ассоциацию родителей и детей с дислексией, чтобы рассказать о своем опыте.
Евгений Гришковец: Когда я все понял, это чуть ли не праздник был! Господи, оказывается, я нормальный человек. Фото: Вячеслав Прокофьев / ТАСС
— Сейчас не модно говорить о гендере, но это невероятно мужской поступок! — приветствовала его учредитель Ассоциации, дочь директора Государственного Эрмитажа Мария Пиотровская.
Большинство россиян, страдающих ею, по словам Пиотровской, этого никогда не делают. Ну разве что на ухо кому-то шепнут. И зря. Судьбы Моцарта, Бетховена, Андерсена, Агаты Кристи, Уолта Диснея, Владимира Маяковского, Мэрилин Монро, Киры Найтли, Генри Форда, Тарантино, Джона Леннона — все они были дислексиками — свидетельствуют, что это расстройство не перечеркивает счастье и успех человека.
Только таким людям нужна помощь. Всех — от неравнодушных людей до неравнодушного государства, разрабатывающего удобные правила и своего рода «доступную среду», только на этот раз интеллектуальную. «РГ» представляет диалог Евгения Гришковца и Марии Пиотровской о внимании к людям, их познавательному своеобразию, упорству, провалам, рискам и достижениям.
Хуже «среднего идиота»
Мария Пиотровская: Что вам родители в детстве говорили?
Евгений Гришковец: Что я лентяй.
Мария Пиотровская: Вы пошли в 1-й класс и вернулись с первой двойкой в тетради.
Евгений Гришковец: Ну, двойка. Наказан. Так педагоги и наказывали — двойками. А одноклассники смеялись. Тогда про дислексию никто не знал. Поэтому от меня все упорно добивались того, чего я сделать не мог. Мои родители меня любили ( и любят). Но мама, преподававшая теплофизику и теплодинамику в университете, видя мой трояк по физике, не могла понять, как это, человек не может выучить физику. Отец доходил до отчаяния, тряс передо мною книжками и кричал: этот учебник написан для среднего идиота! И я в 13 лет понимал, что я хуже «среднего идиота». Когда у папы были припадки педагогики, он разбирал со мною пару задач («Папа у Васи силен в математике»), и я получал свою липовую четверку.
Я не знал тогда, что мое восприятие отличается от восприятия других людей. Я был такой же мальчик, как и все остальные, но у меня не получалось.
Детство все равно было счастливым. Но в какие-то моменты, когда родители настаивали на том, чтобы я что-то понял, а учителя давали задания, которые мне были совершенно не под силу, я был абсолютно несчастным. И очень одиноким. Я никогда не учился легко, мне всегда было тяжело. И это кошмар, когда в школе тебя начинают высмеивать. Я сменил четыре школы, мы переезжали. И когда учился в плохих школах, все было нормально. Но заканчивал я хорошую, с английским уклоном, в ней было престижно хорошо учиться. Я был очень непрестижный парень…
Людвиг ван Бетховен был тоже дислексиком. Фото: ТАСС
Если бы в мое время был ЕГЭ, я бы вообще школу не закончил. Но ЕГЭ тогда не было, и учитель по математике принес мне готовую контрольную работу, чтобы я ее списал. Я списал идеально, и мне справедливо поставили за нее тройку. Тему сочинения мне сказали заранее. Я его устно придумал (короткими предложениями, без запятых), вызубрил наизусть, потом записал на экзамене, и то сделал четыре ошибки… Перед сдачей экзамена по чтению учительница за два часа дала мне текст, я его быстро выучил и на экзамене изображал, что читаю. Иначе бы не уложился ни в какие нормативы. Читал бы как революционные матросы в старых советских фильмах, водя пальцем по депеше.
Мария Пиотровская: Что самое главное для дислексика на экзаменах?
Евгений Гришковец: Для дислексика принципиально сдавать экзамен хорошему, умному преподавателю.
Боцман и шпангоут
Мария Пиотровская: Как вы служили в армии?
Евгений Гришковец: Было нелегко. Я служил на флоте и не мог, например, запомнить и показать, как сигнальщики машут флажками. Или чем отличается шпангоут. Даже если бы я знал, что я дислексик, ну кому там об этом скажешь? Боцману? (Слово «боцман» произносится с нежным юмором, смех в зале и на сцене. — Прим. ред.). Но ничего, я даже достиг результатов и пользовался уважением. А в университете мне было учиться легко. Там все было интересно. И лекции читали совершенно другие, чем в школе, преподаватели, относящиеся к тебе с интересом и уважением. Из-за интереса мне все давалось. Да, я читал дольше, чем другие. Особенно английские романы эпохи Просвещения. Но зато если уж я вгрызался, то запоминал на всю оставшуюся жизнь.
Агате Кристи дислексия не помешала сочинять отменные детективы. Фото: Reuters
Мария Пиотровская: Когда вы все-таки поняли, что вы дислексик?
Евгений Гришковец: Это было, кажется, в 1990-м. Вышел фильм «Твин Пикс», и я, его фанат, прочитал интервью актрисы Лары Флинн Бойл. Она в нем рассказывала, как ей трудно воспринимать знаковую информацию, сценарии ей читают «на слух». Слово «дислексия» не прозвучало, но я все понял. Обрадовался, побежал к родителям. Это чуть ли не праздник был! Господи, оказывается, я нормальный человек. До этого я все время ощущал в себе какую-то ненормальность и отсутствие возможности с этим справиться.
Отцы и дети с дислексией
Мария Пиотровская: У вас из троих детей двое дислексиков…
Евгений Гришковец: Да. Младшая 10-летняя дочка начинает писать с середины страницы, она просто не видит то, что слева. Учительница ее заставляет по 10 раз переписывать, но это ничего не дает. Ребенку-дислексику, если у него в школе не получается, не должно быть тяжело. Поэтому когда все становится понятно, нам, родителям, надо начинать разговаривать с учителями. Поначалу они выслушивают, кивают, но про себя думают: рассказывайте-рассказывайте, все понятно, значит, ребенок сложный, ленивый, вот они и «отмазывают» его в расчете на поблажки. Мы не просвещены по поводу дислексии. Школа — точно.
Мария Пиотровская: Просто с 1991 года все дислексики — а это примерно 25 процентов учеников — перестали существовать как явление. Никто не диагностирует дислексию и не работает с ней.
Евгений Гришковец: Тем более надо всех просвещать. Отличный пример просветительского эффекта — фильм «Человек дождя», лучше всех рассказавший миру об аутизме. Посмотрев его, понимаешь, как ценен, прекрасен и удивителен не только человек с аутизмом, но каждый человек. Моя задача сделать так, чтобы у моих детей было счастливое детство. Моя младшая дочь занялась спортом, начала плавать. Потом балетом, и стала там самой лучшей, веселой и талантливой. И мы с ней вместе решили, что школа — ну ладно,там и на тройки можно… Главное, чтобы у человека было знание, что в чем-то он нормальный и успешный. Что ему есть чем гордиться и его есть за что хвалить. Потому что если работа по математике написана на двойку, то и ребенок с дислексией поймет, что родители врут, хваля его.
Моя старшая дочь Наташа, историк религий, написала уже толстую диссертацию. Мне с ней даже страшно общаться, так она много знает! Хотя дислексик тоже жуткий. Сын не дислексик, но страшно стрессует перед ЕГЭ. Что будет на ЕГЭ с младшей дочерью? Стресс по этому поводу уже испытываем мы с женой.
Мария Пиотровская: Мы полагаем, что дислексикам все-таки нужны альтернативные экзамены. Например, всего два и на выбор.
Клавиатура и руль — это не мое
Мария Пиотровская: Логопед-психолог, придя к моей дочери, попросила ее и меня нарисовать картинку: мальчик с портфелем бежит из школы домой. Я нарисовала обычную, дочь покадровую, как мультфильм. С тех пор я всем дислексикам задаю вопрос: как вы, человек с «другим восприятием», видите мир?
Евгений Гришковец: Трудно это объяснить. В моей жизни до сих пор много вещей, с которыми я не могу справиться. У меня нет компьютера, потому что я не владею клавиатурой. Могу медленно потыкать одним пальцем, но если вдруг размер клавиатуры уменьшится или увеличится, все, я уже не могу. Обновление программы в мобильном телефоне для меня — ужас и невероятное переживание. Смена самого телефона, даже одного его размера — огромный стресс. У меня на телефоне стоит Вайбер, там синие экранчики, я к этому привык. А в Ватсапе зеленые, и я уже так не могу. И вообще две программы для меня беспорядок и ужасный дискомфорт. Я понял, что не смогу научиться водить машину. Теорию освоил легко, а вождение нет. Потому что каждый раз мне нужно заново понимать показания приборов. Мне также трудно сконцентрироваться и смотреть в одном направлении, как это должен делать водитель. И поскольку очень хочется хотя бы раз в жизни проехать на машине одному (смех в зале), жду автомобиля с автопилотом.
Я путал буквы, пропускал слова. И стал думать, что, наверное, я идиот
Мария Пиотровская: А какие преимущества вам дает дислексия?
Евгений Гришковец: Общаясь с другими, я понял, что у меня другие свойства памяти. У меня вся память в активе. Нет каких-то закрытых территорий. Читатели моих книг иногда спрашивают: как вы так замечательно помните детство? Я отвечаю, что это разделение труда — кто-то строит, кто-то лечит, кто-то учит, а я помню.
Репутации Сальвадора Дали дислексия вряд ли повредит. Фото: АР
Советы от Евгения Гришковца
1. Не стоит отделять дислексиков и загонять их в какие-то особые классы. Потому что у детей с дислексией разные формы и степени ее.
2. Не надо внушать человеку, что из-за дислексии ему многое неподвластно. Потому что он скажет: «О, я не могу!» и перестанет прикладывать усилия к тому, с чем бы справился запросто. А может быть, и выдающимся образом.
3. Когда мои дети с дислексией сталкиваются с трудностями в школе, я их успокаиваю: учительница тоже человек, который может ошибаться и не понимать, что с тобой. Она просто не верит, что тебе трудно. А мы с мамой верим.
4. Просвещать надо все-таки взрослых. Одноклассникам не обязательно знать про особенности твоего ребенка. Дети ведь обычно не хотят быть особенными.
5. Дислексики — нормальные люди. Это не болезнь. И не проблема. Это задача. Причем уникальная по каждому человеку.
Ключевой вопрос
Тайны мастерства
Как дислексики пишут настоящие книги?
Евгений Гришковец: У меня не совсем обычная история, я играю много спектаклей. И перейти от гастрольной жизни к писательскому труду, войти в писательское состояние мне не просто. Но войдя в него, ты попадаешь в своего рода «литературную трубу» — превращаешься в существо, которое производит литературу. Как тутовый шелкопряд, который ест-пьет, и из него получается шелк.
Все написанное за день я отдаю жене, она это обрабатывает, я прослушиваю. Кстати, жена единственный человек, который может разбирать мой текст. Почерк-то у меня понятный, но я путаю буквы и многие слова не записываю. Но она, догадываясь по контексту, что и как, все прекрасно расшифровывает.
Пьесы пишу очень быстро. «Собрание сочинений», которая идет сейчас в «Современнике», написал за 12 дней. «Между делом» для Театра им. Пушкина — за 8.
Раньше я не предполагал, что стану писать прозу. Но отчетливо помню, как однажды вечером увидел в трехмерном пространстве книгу, на которой было написано «Евгений Гришковец. Рубашка. Роман». И ко мне пришел замысел этого романа, даже со структурой. Замысел — это не текст, а какой-то огромный объем информации… Он должен отстояться. Чтобы стало понятно, тот ли это замысел. Я реализую, наверное, процентов пятнадцать своих замыслов.
Написание книги — удивительный процесс. Он более всего похож на чтение. Это, в сущности, чтение — только очень медленное. Но когда вы читаете книгу, вы можете ее закрыть и отложить. Вы не знаете, что будет дальше, но книга есть. А когда пишете, то знаете или догадываетесь, что будет дальше, но книги нет. Она появляется у тебя на глазах. Это совершенно магический процесс.
Как связать два слова в одной строке
Помните пишущие машинки? (Те из вас, кто слишком молод, чтобы помнить об этом, просто пропустите эту часть. Пожалуйста. ) Каждый раз, когда вы слышали этот маленький ding , когда вы приближались к правому краю, вы знали, что вам нужно дотянуться вверх, ударьте по этой планке с левой стороны и верните валик к левому краю, чтобы начать новую строку.
Да, это была головная боль по сравнению с набором текста в текстовом редакторе. Но, по крайней мере, тогда у вас был полный контроль над тем, где был разрыв строки.В эти дни? Не так много.
Но вы все равно можете остановить неудобные перерывы — слова с переносом или другие группы слов, которые должны появляться вместе в одной строке — с помощью быстрой комбинации из трех клавиш.
Прекращение неправильной расстановки переносов
Проблема с помещением слова через дефис в конце строки заключается в том, что строка может разорваться прямо на символе дефиса. В некоторых случаях (и для некоторых людей) это действительно не проблема. Но для других это раздражение.
Чтобы этого не произошло, вам понадобится дефис, отличный от стандартного, который вы видите на клавиатуре рядом с цифрой ноль. Вам нужен «мягкий дефис», также известный как «неразрывный дефис».
Чтобы вставить одного из этих младенцев, просто удалите дефис, который у вас уже есть, и, не снимая курсора между словами, которые вы хотите расставить через дефис, нажмите CTRL-SHIFT-HYPHEN (да, это все одновременно, так что вы ‘ мне понадобится небольшая координация, чтобы осуществить это). Новый «мягкий» дефис будет выглядеть как так же, как старый, но никогда больше не допускает разрыв строки посередине.
Объединение слов в одну строку
Что, если бы вы хотели сохранить слова «чрезмерно обременительный» в одной строке, но после «чрезмерно» линия порвалась естественным образом?
Для этого нужно вставить неразрывный пробел между словами «чрезмерно» и «обременительный».”Просто удалите существующий обычный пробел между словами и вставьте неразрывный пробел, используя CTRL-SHIFT-SPACE.
И вот результат:
Обратите внимание, что при включении «Показать / скрыть» отображение неразрывного пробела на экране отличается от обычного символа пробела. Неразрывная — это открытый круг, а обычное пространство — это точка.
Но не волнуйтесь. Ни одна из этих маленьких точек, сплошных или открытых, никогда не печатается. Это просто способ, которым функция Показать / Скрыть представляет различные символы пробела.
Остерегайтесь здесь полного обоснования!
Если вы управляете переносом строк в абзацах с помощью любого из этих методов, и ваши абзацы полностью выровнены по ширине (что означает, что они имеют прямые края на левом и правом полях), вы должны быть осторожны, вы не перенос слишком длинного слова на следующую строку. В противном случае в вашей предыдущей строке будет много лишнего пробела между / внутри слов, что может выглядеть немного неудобно.
Просто руководствуйтесь здравым смыслом. Удачной упаковки!
(фото: petesimon @ Flickr http: // www.flickr.com/photos/petesimon/3365916944/)
определение синтаксического анализа по The Free Dictionary
Бегун прошел в дюжине футов от них, пересек мокрый песок, никогда не разбирая, пока пена не достигла его колен, а над ним, на высоте десяти футов по крайней мере, поднялась вода.Он слишком много видел жизни, и его ум был слишком зрелым, чтобы полностью довольствоваться дробями, кубическим корнем, синтаксическим анализом и анализом; и были времена, когда их разговор касался других тем — последних стихов, которые он прочитал, последнего поэта, которого она изучила. Четыре, шесть или десять лет ученица разбирает греческий и латынь, и как только он уходит из школы. Университет, как это смехотворно называют, закрывает эти книги в последний раз. Там было не менее трех несчастных парней во фраках, с зарождающимися на подбородках, которых Доктор и мастер формы всегда старались поднять. в старшую школу, но чей синтаксический анализ и конструирование сопротивлялись самым благонамеренным толчкам.Galerie Joaquin объединяет двух восходящих мастеров в «Очаровании синтаксического анализа: витрина современных абстракций». Работы скульптора по стеклу Мардж Органо и абстракциониста Омбока Вилламора будут представлены в Северном дворе торгового центра Power Plant в Макати в августе, поэтому мы также можем разобрать слова «мир» и «сохранение». По словам Фила Коэна, главного научного сотрудника отдела искусственного интеллекта компании Voicebox, поставщика голосовых технологий для автомобилей, мобильных устройств, дома и в Интернете, этот синтаксический анализ покинул картину не только годы, но и десятилетия назад. Семантический анализ и аналогичные методы могут произвести революцию в обработке естественного языка. -подключенные устройства.16 октября 2017 года — Калифорнийская американская технологическая компания по найму персонала Rchilli приобрела калифорнийскую компанию по синтаксическому анализу резюме / резюме CandidateZip из США, чтобы укрепить свои позиции в отрасли, сообщила компания. Международная компания по управлению рисками Anvil Group, расположенная в США. Kingdom теперь предлагает своим клиентам решение для синтаксического анализа электронной почты Traxo CAPTURE в качестве встроенной функции в свою ETMS (систему мониторинга поездок сотрудников), которая используется некоторыми из самых известных корпораций по всему миру.В этом сборнике рассказов американка филиппинки Линда Тай-Каспер проводит пальцами по шрамам, оставшимся после исторических событий на Филиппинах, разбирая, что значит пережить и пережить травму диктатуры и войны. (CPA) для текстового анализа и открытий: новые исследования и возможности
Держите текст вместе — Word
Если слово слишком длинное, чтобы поместиться в конце строки, Microsoft Office Word 2007 перемещает слово в начало следующей строки, а не переносит его.Однако вы можете использовать функцию расстановки переносов, чтобы автоматически или вручную расставлять текст через перенос, вставлять необязательные или неразрывные переносы и устанавливать максимально допустимое расстояние между словом и правым полем без переноса слова.
При автоматической расстановке переносов Office Word 2007 автоматически вставляет переносы там, где они необходимы. Если вы отредактируете документ позже и измените разрывы строк, Office Word 2007 изменит перенос текста в документе.
-
Убедитесь, что текст не выделен.
-
На вкладке Макет страницы в группе Параметры страницы щелкните Расстановка переносов , а затем нажмите Автоматически .
Необязательный дефис — это дефис, который используется для определения того, где слово или фраза разрываются, если они попадают в конец строки.Например, вы можете указать, что слово «непечатаемое» прерывается как «непечатаемое» вместо «непечатаемое». Когда вы вставляете необязательный дефис в слово, которое не находится в конце строки, дефис будет виден, только если вы включите Показать / скрыть .
-
На вкладке Home в группе Paragraph щелкните Показать / скрыть .
-
Щелкните слово, в которое вы хотите вставить дополнительный дефис.
-
Нажмите CTRL + ДЕФИС.
Для автоматического переноса части документа выполните следующие действия:
- Выделите текст, который нужно расставить переносом.
-
На вкладке Макет страницы в группе Параметры страницы щелкните Расстановка переносов , а затем нажмите Автоматически .
При переносе текста вручную Office Word 2007 ищет текст для переноса. После того, как вы укажете место переноса текста, Word вставит дополнительный дефис. Если позже вы отредактируете документ и измените разрывы строк, Office Word 2007 отобразит и напечатает только дополнительные дефисы, которые все еще находятся в конце строк. Word не переносит документ заново.
-
Выделите текст, который нужно расставить переносом.
-
На вкладке Макет страницы в группе Параметры страницы щелкните Расстановка переносов , а затем щелкните Вручную .
-
Если Office Word определяет слово или фразу для переноса, выполните одно из следующих действий:
-
Чтобы вставить дополнительный дефис в место, которое предлагает Office Word, щелкните Да .
-
Чтобы вставить дополнительный дефис в другую часть слова, переместите точку вставки в это место и нажмите Да .
-
Неразрывные дефисы предотвращают разрыв переносимых слов, чисел или фраз, если они попадают в конец строки текста.Например, вы можете предотвратить взлом 555-0123; вместо этого весь элемент переместится в начало следующей строки.
-
Щелкните в том месте, где вы хотите вставить неразрывный дефис.
-
Нажмите CTRL + SHIFT + ДЕФИС.
Зона переноса — это максимальное пространство, которое Office Word 2007 допускает между словом и правым полем без переноса слова.Вы можете изменить зону переноса, сделав ее шире или уже. Чтобы уменьшить количество переносов, сделайте зону переносов широкой. Чтобы уменьшить неровность правого поля, сузьте зону переноса.
-
На вкладке Макет страницы в группе Параметры страницы щелкните Расстановка переносов , а затем щелкните Параметры расстановки переносов .
-
В зоне Расстановка переносов введите желаемый размер.
Вы можете удалить все автоматические расстановки переносов и каждый случай расстановки переносов вручную, например, необязательные и неразрывные переносы.
-
Чтобы удалить автоматические расстановки переносов, на вкладке Макет страницы в группе Параметры страницы щелкните Расстановка переносов , а затем нажмите Нет .
-
Чтобы убрать расстановку переносов вручную, на вкладке Домашняя страница в группе Редактирование щелкните Заменить .
-
Если вы не видите кнопку Special , нажмите More .
-
Щелкните Special , а затем щелкните Optional Hyphen , чтобы удалить переносимые вручную дефисы, или Nonbreaking Hyphen , чтобы удалить неразрывные переносы.
-
Оставьте поле Замените пустым.
-
Нажмите Исправить Далее , Заменить или Заменить все .
RegEx — извлечение первых N слов
3 января, 2020
| Ник Ястребски
RegEx — извлечение первых N слов
Недавно мой коллега попросил меня помочь с выражением RegEx для извлечения первого числа N слов из блока текста.
ТАБЛИЦА AU
Извлечь этот текст в Табло не так уж сложно. Нам нужно будет создать новое вычисляемое поле, которое будет содержать наш извлеченный текст, извлекая текст из существующего поля в наших данных. Это поле будет создано с помощью функции REGEXP_EXTRACT вместе с выражением, которое мы создали ранее.
Это вычисление, используемое для извлечения первых 150 слов из поля «Образец текста». Это сравнение между полем «Образец текста» и полем, содержащим первые 150 слов, созданным с использованием вычисленного выше поля.
ALTERYX
Использовать это в Alteryx также довольно просто. Все, что нам нужно сделать, это использовать инструмент RegEx в режиме синтаксического анализа.
Вот конфигурация инструмента RegEx в Alteryx для извлечения первых 150 слов из нашего образца текста. Это наше текстовое поле в Alteryx. Здесь строки слишком длинные, чтобы отображать их все вместе, поскольку предварительный просмотр ячейки не переносит текст. Вот поле, созданное инструментом RegEx, извлекающим первые 150 слов из нашего образца текста.
И вот оно! Даже если вам не нужен вариант использования, я надеюсь, что логика создания выражения будет полезна, чтобы помочь вам лучше понять, как работает RegEx.
Собираем все вместе
Terrapin Logo 4 больше не выпускается! Наш новый Terrapin Logo версия намного мощнее и
современный; мы настоятельно рекомендуем вам обновить нашу последнюю версию
язык программирования Logo.
Этот раздел содержит все команды, которые объединяют слова логотипа или
списки или доступ к элементам слов или списков логотипа.
FPUT
Добавляет элемент к его вводу.
Синтаксис
FPUT слово слово
Список слов FPUT
Список списков FPUT
Описание
FPUT сообщает слово или список, созданный путем ввода первого ввода
в начале второго входа.
сообщает слово; в противном случае он сообщает список. См. Также СПИСОК,
LPUT, ПРЕДЛОЖЕНИЕ и СЛОВО.
Пример
FPUT «A» BC Результат: ABC FPUT 1 23 Результат: 123 FPUT «А [ЗЕЛЕНЫЙ ЧЕВИ] Результат: [ЗЕЛЕНЫЙ ЧЕВИ] FPUT [СЕВЕРНАЯ ДАКОТА] [НЬЮ-ХЭМПШИР] Результат: [[СЕВЕРНАЯ ДАКОТА] НЬЮ-ХЭМПШИР]
ISEQ
Выводит список последовательных целых чисел.
Синтаксис
ISEQ с по
(ISEQ от до приращения)
Описание
ISEQ выводит список целых чисел от FROM до TO, включительно. Если
инкремент задается как необязательный третий вход, создаются целые числа
используя заданное приращение; если приращение не указано, приращение равно 1
если FROM меньше TO, или -1, если FROM больше TO. Обратите внимание, что если
приращение не равно 1 или -1, значение TO может не входить в список;
например, вывод (ISEQ 1 5 3) не будет содержать значение 5,
потому что следующим добавляемым значением было бы 6 вместо 5.
Пример
ISEQ 5 10 Результат: [5 6 7 8 9 10] ISEQ 10 5 Результат: [10 9 8 7 6 5] (ISEQ 5 10 2) Результат: [5 7 9]
СПИСОК
Объединяет свои входные данные в список.
Синтаксис
СПИСОК объект1 объект2
(СПИСОК объект1 объект2 объект3 ...)
Описание
LIST сообщает список, состоящий из его входов. Входы в LIST могут быть
либо слова, либо списки. Если входы в LIST сами по себе являются списками, LIST
сохраняет их в виде списков.LIST ожидает два ввода, но может принимать больше или
меньше, если он и все его входные данные заключены в круглые скобки. Смотрите также
FPUT, LPUT, SENTENCE и WORD.
Пример
СПИСОК «СЕВЕРНАЯ» КАРОЛИНА Результат: [СЕВЕРНАЯ КАРОЛИНА] СПИСОК [БЫТЬ] [ИЛИ НЕ БЫТЬ] Результат: [[БЫТЬ] [ИЛИ НЕ БЫТЬ]]
ЛПУТ
Добавляет элемент к своему вводу.
Синтаксис
LPUT слово слово
Список слов LPUT
Список списка LPUT
Описание
LPUT сообщает о новом объекте, который создается путем помещения первого входа в
конец второго входа.Входы в LPUT могут быть либо словами, либо
списки. Если первый вход — это список, второй не может быть словом. Если
оба входа — слова, LPUT сообщает слово. См. Также СПИСОК,
FPUT, ПРЕДЛОЖЕНИЕ и СЛОВО.
Пример
ЛПУУ «ИССИППИ» МИСС Результат: MISSISSIPPI LPUT [COLORADO] [MISS] Результат: [MISS [COLORADO]] LPUT FIRST [X Y Z] [A B C D] Результат: [A B C D X]
ПАРС
Анализирует строку и выводит список.
Синтаксис
PARSE слово
Описание
PARSE считывает свой ввод и преобразует его в список.
Процедура Listener, которую использует Logo для оценки пользовательского ввода, примерно
написано как:
ДЛЯ СЛУШАТЕЛЯ
ЗАПУСТИТЬ PARSE ПРОЧИТАТЬ ЦИТАТУ
СЛУШАТЕЛЬ
КОНЕЦ
Пример
PARSE «| привет мир | Результат: [HI WORLD] PARSE «| (a b c) | Результат: [(A B C)]
RSEQ
Выводит список рациональных чисел с равным интервалом.
Синтаксис
RSEQ от до подсчета
Описание
RSEQ выводит список COUNT рациональных чисел с равным интервалом между
ОТ и ДО включительно.
Пример
RSEQ 4 5 6 Результат: [4 4,17 4,33 4,5 4,67 4,83]
ПРЕДЛОЖЕНИЕ
Также: SE
Объединяет свои входные данные в список, сглаживая списки.
Синтаксис
SENTENCE объект1 объект2
(SE объект1 объект2 объект3 ...)
Описание
SENTENCE сообщает список, состоящий из его входов. SENTENCE ожидает двух
входов, но будет принимать больше, если он и все его входы заключены в
круглые скобки.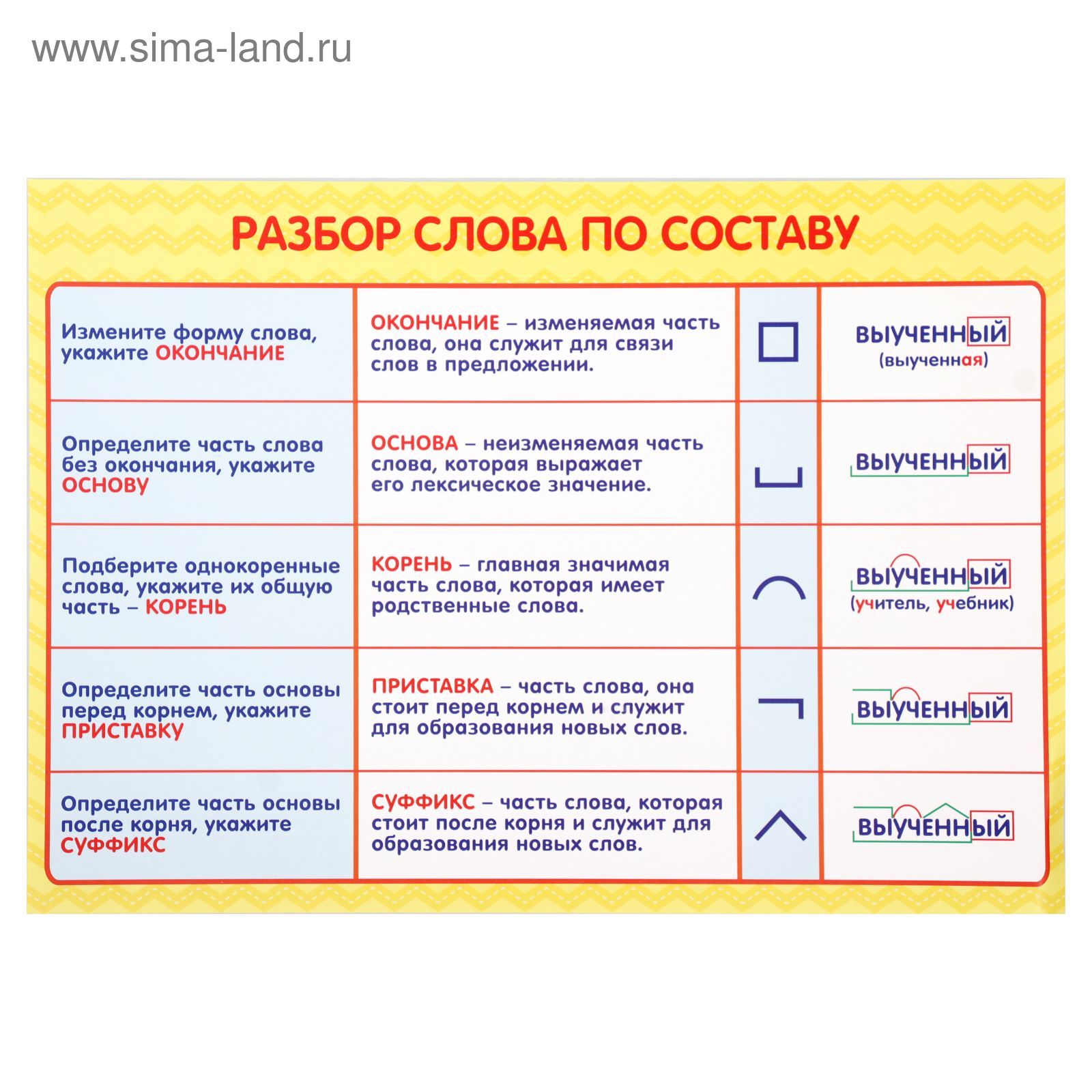
удалены и объединены в один список. См. Также FPUT,
LPUT, LIST и WORD.
Пример
ПРИГЛАШЕНИЕ «САМЫЙ« МЕСЯЦ » Результат: [САМЫЙ ВЕЛИКИЙ МЕСЯЦ] ПРЕДЛОЖЕНИЕ [АПРЕЛЬ] [САМЫЙ ВЕЛИКИЙ МЕСЯЦ] Результат: [АПРЕЛЬ — САМЫЙ ВЕЛИКИЙ МЕСЯЦ]
вместо
Заменяет текст словом или списком.
Синтаксис
SUBST what with wordorlist
Описание
SUBST выполняет замену текста в своих аргументах.Заменяет все
вхождения его первого ввода со вторым вводом внутри слова или
список задан как его третий вход. Если третий вход — список,
замена рекурсивна и влияет на все списки внутри списка. Если
заменяемый элемент списка заключен в кавычки, замененный текст останется в кавычках.
Таким же образом сохраняются ведущие двоеточия.
Пример
Цитаты и двоеточия сохранены.
SUBST «JUNK» NEW [A JUNK BOX] Результат: [НОВАЯ КОРОБКА] SUBST »? «X« A? B? C Результат: AXBXC SUBST »? «МАЙК [ПРИВЕТ? [КАК ДЕЛА ?]] Результат: [ПРИВЕТ, МАЙК [КАК ТЫ МАЙК]]
СЛОВО
Объединяет свои входные данные в слово.
Синтаксис
СЛОВО объект1 объект2
(СЛОВО объект1 объект2 объект3 ...)
Описание
WORD связывает свои входы, которые не должны быть списками, с одним словом.
Пример
СЛОВО «САМЫЙ» МЕСЯЦ Результат: NICESTMONTH
Пакет
nltk.parse — документация NLTK 3.6
>>> from nltk.parse import DependencyGraph, DependencyEvaluator
>>> от nltk.parse.transitionparser import TransitionParser, Configuration, Transition
>>> gold_sent = DependencyGraph ("" "
... Экономичный JJ 2 ATT
... новости NN 3 SBJ
... имеет корень VBD 0
... маленький JJ 5 ATT
... эффект NN 3 OBJ
... на IN 5 ATT
. .. финансовый JJ 8 ATT
... продает NNS 6 PC
.... . 3 УЕ
... "" ")
.. финансовый JJ 8 ATT
... продает NNS 6 PC
.... . 3 УЕ
... "" ")
>>> conf = Конфигурация (gold_sent)
##################### Проверить исходный элемент ###################### #
>>> print (','.присоединиться (conf.extract_features ()))
STK_0_POS_TOP, BUF_0_FORM_Economic, BUF_0_LEMMA_Economic, BUF_0_POS_JJ, BUF_1_FORM_news, BUF_1_POS_NN, BUF_2_POS_VBD, BUF_3_POS_JJ
##################### Проверить переход ######################
Проверьте инициализированную конфигурацию
>>> print (conf)
Стек: [0] Буфер: [1, 2, 3, 4, 5, 6, 7, 8, 9] Дуги: []
-
Выполните некоторые проверки перехода для ARC-STANDARD
>>> операция = Переход ('стандарт дуги')
>>> операция.сдвиг (конф)
>>> operation.left_arc (conf, "ATT")
>>> operation.shift (conf)
>>> operation.left_arc (conf, "SBJ")
>>> operation.shift (conf)
>>> operation.shift (conf)
>>> operation.left_arc (conf, "ATT")
>>> operation.shift (conf)
>>> operation.shift (conf)
>>> operation.shift (conf)
>>> operation.left_arc (conf, "ATT")
Средняя проверка конфигурации и функций
>>> print (conf)
Стек: [0, 3, 5, 6] Буфер: [8, 9] Дуги: [(2, ‘ATT’, 1), (3, ‘SBJ’, 2), (5, ‘ATT’, 4) , (8, ‘ATT’, 7)]
>>> print (','.присоединиться (conf.extract_features ()))
STK_0_FORM_on, STK_0_LEMMA_on, STK_0_POS_IN, STK_1_POS_NN, BUF_0_FORM_markets, BUF_0_LEMMA_markets, BUF_0_POS_NNS, BUF_1_FORM_., BUF_1_PAT_., BUF_0_LDEP
>>> operation.right_arc (conf, "ПК") >>> operation.right_arc (conf, "ATT") >>> operation.right_arc (conf, "OBJ") >>> operation.shift (conf) >>> operation.right_arc (conf, "PU") >>> operation.right_arc (conf, "ROOT") >>> operation.shift (conf)
Завершенная проверка конфигурации
>>> print (conf)
Стек: [0] Буфер: [] Дуги: [(2, ‘ATT’, 1), (3, ‘SBJ’, 2), (5, ‘ATT’, 4), (8, ‘ATT’, 7 ), (6, ‘PC’, 8), (5, ‘ATT’, 6), (3, ‘OBJ’, 5), (3, ‘PU’, 9), (0, ‘ROOT’, 3 )]
-
Выполните некоторые проверки перехода для ARC-EAGER
>>> conf = Конфигурация (gold_sent)
>>> operation = Transition ('arc-eager')
>>> операция. сдвиг (конф)
>>> operation.left_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'SBJ')
>>> operation.right_arc (conf, 'ROOT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'OBJ')
>>> operation.right_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'ПК')
>>> operation.reduce (conf)
>>> операция.уменьшить (конф)
>>> operation.reduce (conf)
>>> operation.right_arc (conf, 'PU')
>>> print (conf)
Стек: [0, 3, 9] Буфер: [] Дуги: [(2, 'ATT', 1), (3, 'SBJ', 2), (0, 'ROOT', 3), (5, ' АТТ ', 4), (3,' OBJ ', 5), (5,' АТТ ', 6), (8,' АТТ ', 7), (6,' PC ', 8), (3,' ПУ ', 9)]
сдвиг (конф)
>>> operation.left_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'SBJ')
>>> operation.right_arc (conf, 'ROOT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'OBJ')
>>> operation.right_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'ПК')
>>> operation.reduce (conf)
>>> операция.уменьшить (конф)
>>> operation.reduce (conf)
>>> operation.right_arc (conf, 'PU')
>>> print (conf)
Стек: [0, 3, 9] Буфер: [] Дуги: [(2, 'ATT', 1), (3, 'SBJ', 2), (0, 'ROOT', 3), (5, ' АТТ ', 4), (3,' OBJ ', 5), (5,' АТТ ', 6), (8,' АТТ ', 7), (6,' PC ', 8), (3,' ПУ ', 9)]
##################### Проверить функцию обучения ######################
A. Проверьте обучение ARC-STANDARD
>>> импортировать временный файл
>>> import os
>>> input_file = временный файл.NamedTemporaryFile (prefix = ’transition_parse.train’, dir = tempfile.gettempdir (), delete = False)
>>> parser_std = TransitionParser ('стандарт дуги')
>>> print (',' .join (parser_std._create_training_examples_arc_std ([gold_sent], input_file)))
Количество обучающих примеров: 1
Количество валидных (проективных) примеров: 1
SHIFT, LEFTARC: ATT, SHIFT, LEFTARC: SBJ, SHIFT, SHIFT, LEFTARC: ATT, SHIFT, SHIFT, SHIFT, LEFTARC: ATT, RIGHTARC: PC, RIGHTARC: ATT, RIGHTARC: OBJ, SHIFT PU, RIGHTARC: КОРЕНЬ, СДВИГ
>>> parser_std.поезд ([gold_sent], 'temp.arcstd.model', verbose = False) Количество обучающих примеров: 1 Количество валидных (проективных) примеров: 1 >>> удалить (input_file.name)
-
Проверить курс обучения ARC-EAGER
>>> input_file = tempfile.NamedTemporaryFile (prefix = 'transition_parse.train', dir = tempfile.gettempdir (), delete = False)
>>> parser_eager = TransitionParser ('нетерпеливый')
>>> print (',' .join (parser_eager._create_training_examples_arc_eager ([gold_sent], input_file)))
Количество обучающих примеров: 1
Количество валидных (проективных) примеров: 1
SHIFT, LEFTARC: ATT, SHIFT, LEFTARC: SBJ, RIGHTARC: ROOT, SHIFT, LEFTARC: ATT, RIGHTARC: OBJ, RIGHTARC: ATT, SHIFT, LEFTARC: ATT, RIGHTARC: PC, УМЕНЬШИТЬ, УМЕНЬШИТЬ, УМЕНЬШИТЬ, УМЕНЬШИТЬ
>>> parser_eager.
Содержание:
Непрерывность функции
Пусть х есть некоторое значение данной переменной величины. Наряду с х рассмотрим другое значение х1 этой переменной величины. Введем следующее определение.
Определение: Приращением переменной величины называется разность между новым значением этой величины и ее прежним значением, т. е. в нашем случае приращение переменной величины равно
Для обозначения приращения используется греческая буква
Прибавляя к значению переменной величины ее приращение, получаем приращенное значение этой величины. Например, 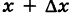
Предположим, что у есть некоторая функция от аргумента х, т. е.
Дадим аргументу х приращение 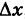
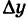
Из равенств (1) и (2) следует
Пример:
Определить приращение аргумента х и приращение функции у = х2, если аргумент х изменился от -1 до 2.
Решение:
Здесь, очевидно, 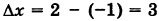
Понятие приращения функции поясним геометрически. Пусть кривая АВ есть график функции у = f(x) (рис. 93).
Рассмотрим на этой кривой точку М с текущими координатами х и у. Дадим абсциссе х точки М(х, у) приращение 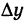
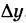
Может случиться, что для некоторого х при стремлении Ах к нулю точка М’ неограниченно приближается к точке М и, следовательно, 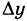
Определение: Функция f(x), определенная на множестве X, называется непрерывной при х = х1 (или непрерывной в точке х1)у если:
1)функция определена при 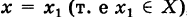
2)приращение функции в точке х1 стремится к нулю, когда приращение аргумента 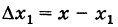
где бесконечно малое приращение 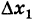
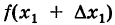
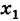
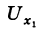
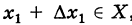
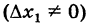
Короче говоря, функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Используя понятие предела функции, получаем развернутое определение непрерывности функции в точке: функция f(x) непрерывна в точке х1 тогда и только тогда, когда 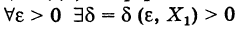
если 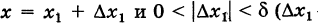
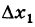
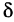
Определение: Функция fix) называется не прерывной на данном множестве X, если: 1) она определена на этом множестве 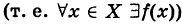
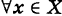
где
Замечание. Множество X здесь трактуется как область определения функции, т. е. точки 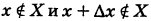
Например, функция fix) непрерывна на отрезке 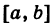
1)эта функция определена в каждой точке этого отрезка,
2)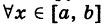
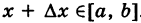
Пример:
Функция
непрерывна на отрезке X = [0, 1], хотя она не является непрерывной на оси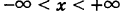
Пример:
Исследовать на непрерывность функцию 
Решение:
Давая аргументу х приращение 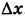
где 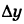
Очевидно, каково бы ни было фиксированное значение х, если 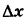
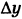
Легко также доказать непрерывность степенной функции 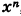
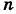
Определение: Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции.
Если х = х0 — точка разрыва функции у = f(x), то возможны два случая:
1)функция f(x} определена при х = х0, причем
2)функция f(x) не определена при х = х0 и говорить о приращении функции в точке х0 не имеет смысла. В этом случае условимся х = х0 называть точкой разрыва функции f(x) только тогда, когда функция fix) определена в непосредственной близости значения х0
То есть при любом 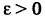
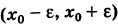
Если можно изменить или дополнительно определить функцию f(x) в точке х0 (т. е. выбрать число f(x0)) так, что измененная или пополненная функция f(x) будет непрерывна при х = х0, то эта точка называется устранимой точкой разрыва функции f(x). В противном случае, т. е. когда функция f(x) остается разрывной при х = х0 при любом выборе числа f(x0), значение х0 называется неустранимой точкой разрыва функции f(x).
Пример:
Рассмотрим функцию Е(х), равную целой части числа х, т. е. если 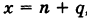
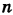
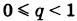
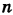
Например, E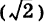
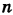
Функция Е(х) разрывна при каждом целочисленном значении аргумента х. В самом деле, например, при х = 1 и достаточно малом 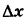
Отсюда, приняв во внимание, что Е(1) = 1, получим
Следовательно, приращение функции 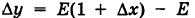
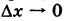
Аналогичное рассуждение можно провести для каждого из значений х = kt где k — целое число. Итак, точки х = k (k = 0, ±1, ±2,…) — неустранимые точки разрыва функции Е(х).
Пример:
Пусть 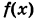
Эта функция не определена при х = 2, но имеет смысл для всех значений х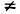
при 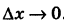
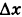
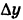
Другое определение непрерывности функции
Ввиду важности понятия непрерывности функции дадим другое определение непрерывности в точке, эквивалентное приведенному выше.
Определение: Функция f(x) называется непрерывной при 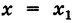
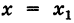
т. е. функция непрерывна в данной точке 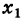
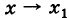
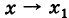
Легко видеть, что:
1)если функция f(x) непрерывна при 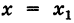
то, полагая х, + 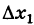
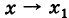

Следовательно, функция f(x) непрерывна также при 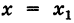
Здесь, как обычно, предполагается, что 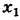
2)очевидно, что, и обратно, из равенства (3) вытекает равенство (2).
Таким образом, эквивалентность двух определений полностью доказана.
Для функции, непрерывной на множестве X, в силу формулы (1) для каждого значения 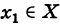
Так как 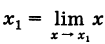
т. е. если функция непрерывна, то знаки предела и функции перестановочны.
В подробных курсах анализа доказывается, что формула (4) остается верной для любой непрерывной функции 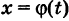
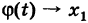
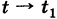
Из определения 3 вытекает, что функция разрывна в данной точке тогда и только тогда, когда: или 1) не существует предела функции в этой точке, или же 2) предел функции в данной точке существует, но не совпадает со значением функции в этой точке.
Непрерывность основных элементарных функций
1)Степенная функция
(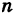
2)Показательная функция
(см. рис. 63) непрерывна при любом значении х. 138
3)Тригонометрическая функция
(см. рис. 65) непрерывна при каждом значении х.
В самом деле, давая аргументу х приращение 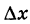
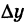
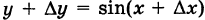
В силу замечания к теореме при 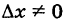
кроме того,
Поэтому
Следовательно, функция sin х непрерывна в интервале 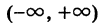
Совершенно так же доказывается, что
есть непрерывная функция в интервале 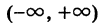
Основные теоремы о непрерывных функциях
Теорема: Сумма конечного числа непрерывных функций есть функция непрерывная.
Доказательство: В самом деле, если 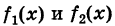
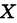
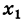
Предполагается, что все рассматриваемые функции определены и непрерывны на некотором общем множестве X (например, на интервале (а, b) или отрезке [а, b] и т. п.).
т. е. предел суммы при 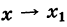
Следовательно, функция 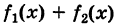
Теорема: Произведение конечного числа непрерывных функций есть функция непрерывная.
Доказательство аналогичное.
Следствие. Целый полином
есть функция непрерывная.
Теорема: Частное от деления двух непрерывных функций есть функция, непрерывная во всех точках, в которых делитель отличен от нуля.
Доказательство аналогичное.
Следствие. Дробная рациональная функция
непрерывна всюду, за исключением тех значений х, где знаменатель обращается в нуль.
Теорема: Непрерывная функция от непрерывной функции есть функция также непрерывная; иначе говоря, сложная функция, состоящая из непрерывных функций, непрерывна.
Доказательство: Пусть 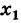
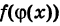
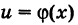
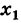
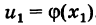
т. е. сложная функция 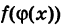
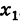
В силу теоремы 4, например, функции 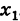
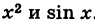
Функции, которые мы будем рассматривать в дальнейшем, непрерывны всюду, кроме, быть может, отдельных значений аргумента.
Например, функция
(см. рис. 66) в силу теоремы 3 настоящего параграфа непрерывна для всех значений аргумента х, кроме тех, для которых cos х = О, т. е. кроме значений 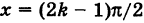
(см. рис. 66) непрерывна при 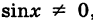
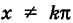
Справедлива теорема о непрерывности обратной функции, которую мы приводим без доказательства.
Теорема: Если функция у = f(x) непрерывна и строго монотоннана промежутке 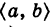
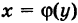
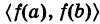
В силу этой теоремы радикал 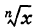
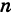
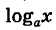
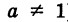
Раскрытие неопределенностей
Может случиться, что функция f(x) определена и непрерывна всюду, за исключением некоторого значения 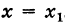
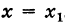
В силу предыдущего для этого необходимо и достаточно выполнение равенства
Операция нахождения предела функции f(x) при 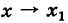
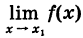
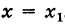
То есть f(x) или строго возрастает, или строго убывает на 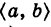
Пример:
Пусть
Эта функция теряет смысл при х = 2. Полагая дополнительно
получим функцию, непрерывную всюду, в том числе и при х = 2. Если же положить 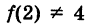
Пример:
Функция
не определена при х = 0. Полагая дополнительно
мы получим функцию, определенную и непрерывную для всех значений аргумента х.
Классификация точек разрыва функции
Точка х0 разрыва функции f(x) называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции (рис. 87):
(при этом функция f(x) не обязательно должна быть определена в точке х0, т. е. f(x0) может не существовать). Величина
называется скачком функции f(x) в точке х0.
Все прочие точки разрыва хх функции f(x) называются ее точками разрыва второго рода. Среди них важное значение имеют точки бесконечного разрыва х1, для которых существуют (конечные или бесконечные) односторонние пределы
и хотя бы один из них является бесконечным (см., например, рис. 98).
В этом случае прямая 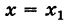
Функция, допускающая на данном промежутке лишь точки разрыва первого рода в конечном числе, называется кусочно-непрерывной на этом промежутке. Заметим, что в точках разрыва кусочно-непрерывная функция может быть не определена. Отметим, что для непрерывности функции f(x) в точке х0 необходимо и достаточно равенства трех чисел:
Пример:
Определить характер точки разрыва х0 = 0 функции
Решение:
Здесь мы имеем
Следовательно, х0 = 0 есть точка разрыва первого рода.
Непрерывность функции
Определение 5.1. Пусть функция y=f(x) определена в некоторой окрестности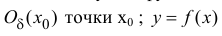
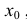
Функция y=f(x) непрерывна на множестве Х , если она непрерывна в каждой точке этого множества.
Точка, в которой функция не является непрерывной, называется точкой
разрыва.
П р и м е р 5.1
Функция 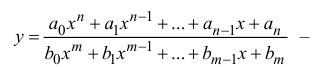
П р и м е р 5.2
Функции
Функция 
- Заказать решение задач по высшей математике
П р и м е р 5.3
Рассмотрим функцию Дирихле: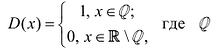
Определение 5.2. Функция y=f(x) называется непрерывной слева (справа) в точке
П р и м е р 5.4
Единичная функция Хевисайда: 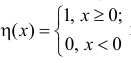
Теорема 5.1. Пусть функции 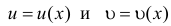
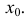
Тогда и функции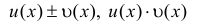
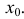
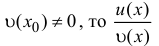
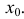
Доказательство следует из теоремы 3.3 и определения 5.1.
Определение 5.3. Пусть функция u=u(x ) определена на множестве Х со
значениями во множестве U и функция y=f(u ) определена на множестве U
со значениями во множестве Y. Тогда функцию 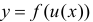
сложной функцией 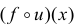
Теорема 5.2. Пусть функция 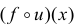
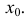
u=u(x ) непрерывна в точке 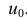
непрерывна в точке 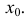
Доказательство следует из определения 3.2 и определения 5.1.
П р и м е р 5.5
Исследовать на непрерывность функцию
в зависимости от значений а .
Р е ш е н и е
Функция 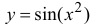
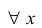
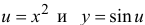
По теореме 5.1 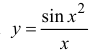
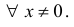
Поэтому при 0 =a функция непрерывна 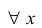
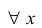
Определение 5.4. Пусть функция y=f(x) определена в некоторой окрестности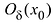
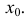
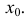
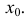
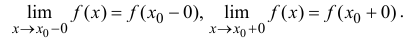
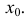
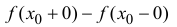
П р и м е р 5.6
Для функции 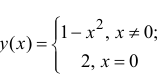
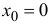
Для функции 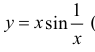
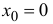
Для функции s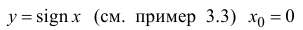
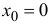
Для единичной функции Хевисайда 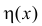
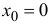
разрыва 1-го рода. Разрыв – неустранимый. Скачок функции в точке 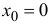
Определение 5.5. Пусть функция y=f(x) определена в некоторой окрестности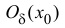
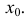
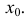
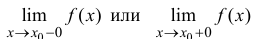
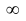
П р и м е р 5.7
Для функций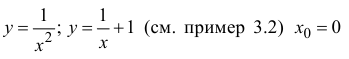
Для функции 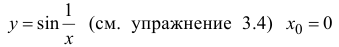
Для функций 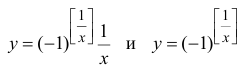
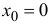
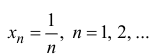
Для функции 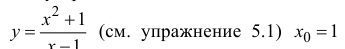
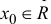
П р и м е р 5.8
Исследовать на непрерывность и найти точки разрыва функции 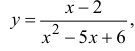
Р е ш е н и е
Функция – дробно-рациональная. Непрерывна везде, кроме точек, где знаменатель обращается в ноль:
Рассмотрим точку 2= x.
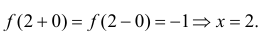
Рассмотрим точку x=3.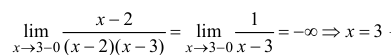
П р и м е р 5.9
Исследовать на непрерывность и определить тип точек разрыва для
функции:
Р е ш е н и е
Функции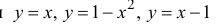
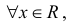
и справа от точек x=±1 функция задается различными аналитическими
выражениями.
Пусть x=1
то есть 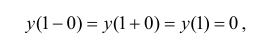
Пусть x=-1
то есть 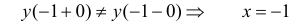
П р и м е р 5.10
Исследовать на непрерывность функцию 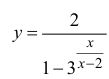
Р е ш е н и е
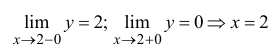
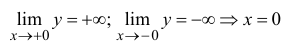
П р и м е р 5.11
Определить тип точек разрыва функции 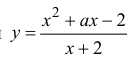
Р е ш е н и е
x =-2 – точка разрыва функции. Найдем
Разбор частей речи
Далее давайте разберем морфологические признаки каждой из частей речи русского языка на примерах. Согласно лингвистике русского языка, выделяют три группы из 10 частей речи, по общим признакам:
1. Самостоятельные части речи:
- существительные (см. морфологические нормы сущ. );
- глаголы:
-
- причастия;
- деепричастия;
- прилагательные;
- числительные;
- местоимения;
- наречия;
2. Служебные части речи:
- предлоги;
- союзы;
- частицы;
3. Междометия.
Ни в одну из классификаций (по морфологической системе) русского языка не попадают:
- слова да и нет, в случае, если они выступают в роли самостоятельного предложения.
- вводные слова: итак, кстати, итого, в качестве отдельного предложения, а так же ряд других слов.
Морфологический разбор существительного
План морфологического разбора существительного
Пример:
«Малыш пьет молоко.»
Малыш (отвечает на вопрос кто?) – имя существительное;
- начальная форма – малыш;
- постоянные морфологические признаки: одушевленное, нарицательное, конкретное, мужского рода, I -го склонения;
- непостоянные морфологические признаки: именительный падеж, единственное число;
- при синтаксическом разборе предложения выполняет роль подлежащего.
Морфологический разбор слова «молоко» (отвечает на вопрос кого? Что?).
- начальная форма – молоко;
- постоянная морфологическая характеристика слова: среднего рода, неодушевленное, вещественное, нарицательное, II -е склонение;
- изменяемые признаки морфологические: винительный падеж, единственное число;
- в предложении прямое дополнение.
Приводим ещё один образец, как сделать морфологический разбор существительного, на основе литературного источника:
«Две дамы подбежали к Лужину и помогли ему встать. Он ладонью стал сбивать пыль с пальто. (пример из: «Защита Лужина», Владимир Набоков).»
Дамы (кто?) — имя существительное;
- начальная форма — дама;
- постоянные морфологические признаки: нарицательное, одушевленное, конкретное, женского рода, I склонения;
- непостоянная морфологическая характеристика существительного: единственное число, родительный падеж;
- синтаксическая роль: часть подлежащего.
Лужину (кому?) — имя существительное;
- начальная форма — Лужин;
- верная морфологическая характеристика слова: имя собственное, одушевленное, конкретное, мужского рода, смешанного склонения;
- непостоянные морфологические признаки существительного: единственное число, дательного падежа;
- синтаксическая роль: дополнение.
Ладонью (чем?) — имя существительное;
- начальная форма — ладонь;
- постоянные морфологические признаки: женского рода, неодушевлённое, нарицательное, конкретное, I склонения;
- непостоянные морфо. признаки: единственного числа, творительного падежа;
- синтаксическая роль в контексте: дополнение.
Пыль (что?) — имя существительное;
- начальная форма — пыль;
- основные морфологические признаки: нарицательное, вещественное, женского рода, единственного числа, одушевленное не охарактеризовано, III склонения (существительное с нулевым окончанием);
- непостоянная морфологическая характеристика слова: винительный падеж;
- синтаксическая роль: дополнение.
(с) Пальто (С чего?) — существительное;
- начальная форма — пальто;
- постоянная правильная морфологическая характеристика слова: неодушевленное, нарицательное, конкретное, среднего рода, несклоняемое;
- морфологические признаки непостоянные: число по контексту невозможно определить, родительного падежа;
- синтаксическая роль как члена предложения: дополнение.
Морфологический разбор прилагательного
Имя прилагательное — это знаменательная часть речи. Отвечает на вопросы Какой? Какое? Какая? Какие? и характеризует признаки или качества предмета. Таблица морфологических признаков имени прилагательного:
- начальная форма в именительном падеже, единственного числа, мужского рода;
- постоянные морфологические признаки прилагательных:
-
- разряд, согласно значению:
-
- — качественное (теплый, молчаливый);
- — относительное (вчерашний, читальный);
- — притяжательное (заячий, мамин);
- степень сравнения (для качественных, у которых этот признак постоянный);
- полная / краткая форма (для качественных, у которых этот признак постоянный);
- непостоянные морфологические признаки прилагательного:
-
- качественные прилагательные изменяются по степени сравнения (в сравнительных степенях простая форма, в превосходных — сложная): красивый-красивее-самый красивый;
- полная или краткая форма (только качественные прилагательные);
- признак рода (только в единственном числе);
- число (согласуется с существительным);
- падеж (согласуется с существительным);
- синтаксическая роль в предложении: имя прилагательное бывает определением или частью составного именного сказуемого.
План морфологического разбора прилагательного
Пример предложения:
Полная луна взошла над городом.
Полная (какая?) – имя прилагательное;
- начальная форма – полный;
- постоянные морфологические признаки имени прилагательного: качественное, полная форма;
- непостоянная морфологическая характеристика: в положительной (нулевой) степени сравнения, женский род (согласуется с существительным), именительный падеж;
- по синтаксическому анализу — второстепенный член предложения, выполняет роль определения.
Вот еще целый литературный отрывок и морфологический разбор имени прилагательного, на примерах:
Девушка была прекрасна: стройная, тоненькая, глаза голубые, как два изумительных сапфира, так и заглядывали к вам в душу.
Прекрасна (какова?) — имя прилагательное;
- начальная форма — прекрасен (в данном значении);
- постоянные морфологические нормы: качественное, краткое;
- непостоянные признаки: положительная степень сравнения, единственного числа, женского рода;
- синтаксическая роль: часть сказуемого.
Стройная (какая?) — имя прилагательное;
- начальная форма — стройный;
- постоянные морфологические признаки: качественное, полное;
- непостоянная морфологическая характеристика слова: полное, положительная степень сравнения, единственное число, женский род, именительный падеж;
- синтаксическая роль в предложении: часть сказуемого.
Тоненькая (какая?) — имя прилагательное;
- начальная форма — тоненький;
- морфологические постоянные признаки: качественное, полное;
- непостоянная морфологическая характеристика прилагательного: положительная степень сравнения, единственное число, женского рода, именительного падежа;
- синтаксическая роль: часть сказуемого.
Голубые (какие?) — имя прилагательное;
- начальная форма — голубой;
- таблица постоянных морфологических признаков имени прилагательного: качественное;
- непостоянные морфологические характеристики: полное, положительная степень сравнения, множественное число, именительного падежа;
- синтаксическая роль: определение.
Изумительных (каких?) — имя прилагательное;
- начальная форма — изумительный;
- постоянные признаки по морфологии: относительное, выразительное;
- непостоянные морфологические признаки: множественное число, родительного падежа;
- синтаксическая роль в предложении: часть обстоятельства.
Морфологические признаки глагола
Согласно морфологии русского языка, глагол — это самостоятельная часть речи. Он может обозначать действие (гулять), свойство (хромать), отношение (равняться), состояние (радоваться), признак (белеться, красоваться) предмета. Глаголы отвечают на вопрос что делать? что сделать? что делает? что делал? или что будет делать? Разным группам глагольных словоформ присущи неоднородные морфологические характеристики и грамматические признаки.
Морфологические формы глаголов:
- начальная форма глагола — инфинитив. Ее так же называют неопределенная или неизменяемая форма глагола. Непостоянные морфологические признаки отсутствуют;
- спрягаемые (личные и безличные) формы;
- неспрягаемые формы: причастные и деепричастные.
Морфологический разбор глагола
- начальная форма — инфинитив;
- постоянные морфологические признаки глагола:
-
- переходность:
-
- переходный (употребляется с существительными винительного падежа без предлога);
- непереходный (не употребляется с существительным в винительном падеже без предлога);
- возвратность:
-
- возвратные (есть -ся, -сь);
- невозвратные (нет -ся, -сь);
- вид:
-
- несовершенный (что делать?);
- совершенный (что сделать?);
- спряжение:
-
- I спряжение (дела-ешь, дела-ет, дела-ем, дела-ете, дела-ют/ут);
- II спряжение (сто-ишь, сто-ит, сто-им, сто-ите, сто-ят/ат);
- разноспрягаемые глаголы (хотеть, бежать);
- непостоянные морфологические признаки глагола:
-
- наклонение:
-
- изъявительное: что делал? что сделал? что делает? что сделает?;
- условное: что делал бы? что сделал бы?;
- повелительное: делай!;
- время (в изъявительном наклонении: прошедшее/настоящее/будущее);
- лицо (в настоящем/будущем времени, изъявительного и повелительного наклонения: 1 лицо: я/мы, 2 лицо: ты/вы, 3 лицо: он/они);
- род (в прошедшем времени, единственного числа, изъявительного и условного наклонения);
- число;
- синтаксическая роль в предложении. Инфинитив может быть любым членом предложения:
-
- сказуемым: Быть сегодня празднику;
- подлежащим :Учиться всегда пригодится;
- дополнением: Все гости просили ее станцевать;
- определением: У него возникло непреодолимое желание поесть;
- обстоятельством: Я вышел пройтись.
Морфологический разбор глагола пример
Чтобы понять схему, проведем письменный разбор морфологии глагола на примере предложения:
Вороне как-то Бог послал кусочек сыру… (басня, И. Крылов)
Послал (что сделал?) — часть речи глагол;
- начальная форма — послать;
- постоянные морфологические признаки: совершенный вид, переходный, 1-е спряжение;
- непостоянная морфологическая характеристика глагола: изъявительное наклонение, прошедшего времени, мужского рода, единственного числа;
- синтаксическая роль в предложении: сказуемое.
Следующий онлайн образец морфологического разбора глагола в предложении:
Какая тишина, прислушайтесь.
Прислушайтесь (что сделайте?) — глагол;
- начальная форма — прислушаться;
- морфологические постоянные признаки: совершенный вид, непереходный, возвратный, 1-го спряжения;
- непостоянная морфологическая характеристика слова: повелительное наклонение, множественное число, 2-е лицо;
- синтаксическая роль в предложении: сказуемое.
План морфологического разбора глагола онлайн бесплатно, на основе примера из целого абзаца:
— Его нужно предостеречь.
— Не надо, пусть знает в другой раз, как нарушать правила.
— Что за правила?
— Подождите, потом скажу. Вошел! («Золотой телёнок», И. Ильф)
Предостеречь (что сделать?) — глагол;
- начальная форма — предостеречь;
- морфологические признаки глагола постоянные: совершенный вид, переходный, невозвратный, 1-го спряжения;
- непостоянная морфология части речи: инфинитив;
- синтаксическая функция в предложении: составная часть сказуемого.
Пусть знает (что делает?) — часть речи глагол;
- начальная форма — знать;
- постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянная морфология глагола: повелительное наклонение, единственного числа, 3-е лицо;
- синтаксическая роль в предложении: сказуемое.
Нарушать (что делать?) — слово глагол;
- начальная форма — нарушать;
- постоянные морфологические признаки: несовершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянные признаки глагола: инфинитив (начальная форма);
- синтаксическая роль в контексте: часть сказуемого.
Подождите (что сделайте?) — часть речи глагол;
- начальная форма — подождать;
- постоянные морфологические признаки: совершенный вид, невозвратный, переходный, 1-го спряжения;
- непостоянная морфологическая характеристика глагола: повелительное наклонение, множественного числа, 2-го лица;
- синтаксическая роль в предложении: сказуемое.
Вошел (что сделал?) — глагол;
- начальная форма — войти;
- постоянные морфологические признаки: совершенный вид, невозвратный, непереходный, 1-го спряжения;
- непостоянная морфологическая характеристика глагола: прошедшее время, изъявительное наклонение, единственного числа, мужского рода;
- синтаксическая роль в предложении: сказуемое.








 split (), .join () и list ().
split (), .join () и list ().  >>> печать (привет)
Привет мама,
Привет папа.
>>> привет.расколоть()
[«Привет», «мама», «Привет», «отец».]
>>> hi.split (' n')
[«Привет, мама», «Привет, отец».]
>>> печать (привет)
Привет мама,
Привет папа.
>>> привет.расколоть()
[«Привет», «мама», «Привет», «отец».]
>>> hi.split (' n')
[«Привет, мама», «Привет, отец».]




 .. финансовый JJ 8 ATT
... продает NNS 6 PC
.... . 3 УЕ
... "" ")
.. финансовый JJ 8 ATT
... продает NNS 6 PC
.... . 3 УЕ
... "" ")
 сдвиг (конф)
>>> operation.left_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'SBJ')
>>> operation.right_arc (conf, 'ROOT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'OBJ')
>>> operation.right_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'ПК')
>>> operation.reduce (conf)
>>> операция.уменьшить (конф)
>>> operation.reduce (conf)
>>> operation.right_arc (conf, 'PU')
>>> print (conf)
Стек: [0, 3, 9] Буфер: [] Дуги: [(2, 'ATT', 1), (3, 'SBJ', 2), (0, 'ROOT', 3), (5, ' АТТ ', 4), (3,' OBJ ', 5), (5,' АТТ ', 6), (8,' АТТ ', 7), (6,' PC ', 8), (3,' ПУ ', 9)]
сдвиг (конф)
>>> operation.left_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'SBJ')
>>> operation.right_arc (conf, 'ROOT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'OBJ')
>>> operation.right_arc (conf, 'ATT')
>>> operation.shift (conf)
>>> operation.left_arc (conf, 'ATT')
>>> operation.right_arc (conf, 'ПК')
>>> operation.reduce (conf)
>>> операция.уменьшить (конф)
>>> operation.reduce (conf)
>>> operation.right_arc (conf, 'PU')
>>> print (conf)
Стек: [0, 3, 9] Буфер: [] Дуги: [(2, 'ATT', 1), (3, 'SBJ', 2), (0, 'ROOT', 3), (5, ' АТТ ', 4), (3,' OBJ ', 5), (5,' АТТ ', 6), (8,' АТТ ', 7), (6,' PC ', 8), (3,' ПУ ', 9)]