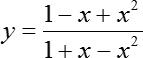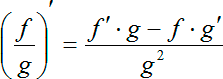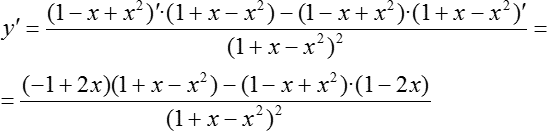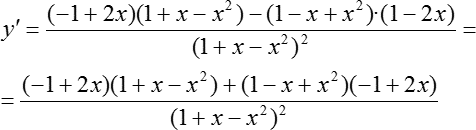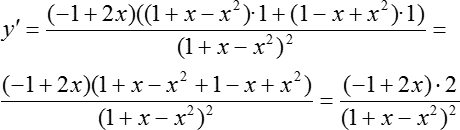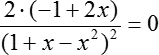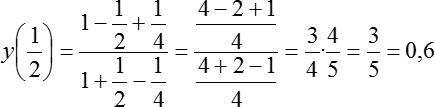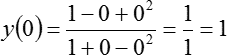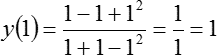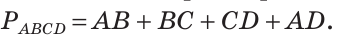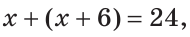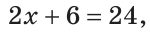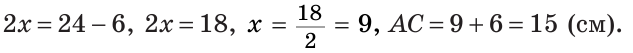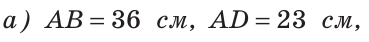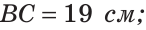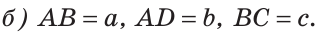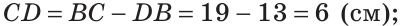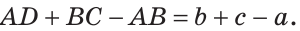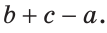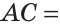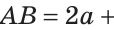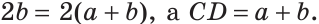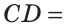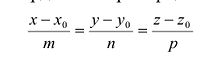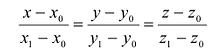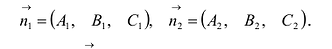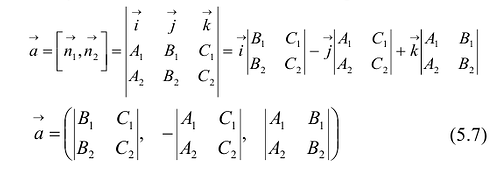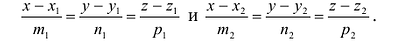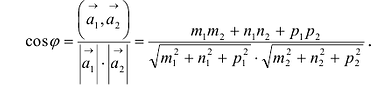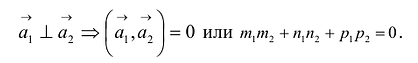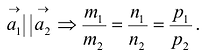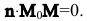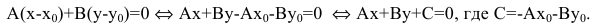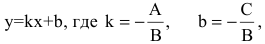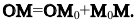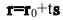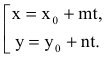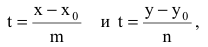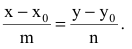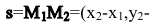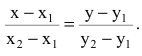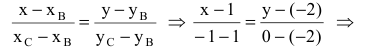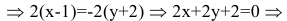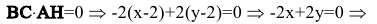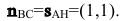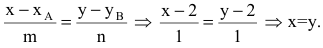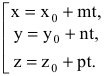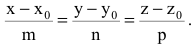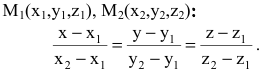Сегодня мы продолжаем изучать задачи на наибольшее и наименьшее значение из ЕГЭ по математике. Теперь перед нами довольно серьезная задача, в которой придется использовать формулу производной частного. Итак:
Задача B15. Найдите наименьшее значение функции на отрезке [0; 1]:
Нахождение наименьшего значения функции на отрезке: универсальный алгоритм
В первую очередь вспомним: как вообще решаются задачи такого типа, в которых требуется найти наименьшее или наибольшее значение функции? Решение таких задач состоит из нескольких этапов:
- В первую очередь, нам предстоит производную: f’;
- Затем мы приравниваем производную к нулю и находим корни. Эти точки являются кандидатами в точки максимума и минимума, т. е. кандидатами в экстремумы: f’ = 0;
- Затем из всех найденных корней мы выбираем те, которые лежат у нас на отрезке. В нашем случае речь идет об отрезке [0; 1]. Следовательно, нам нужно найти такие x_{1}, x_{2}, которые, с одной стороны, являются корнями уравнения f’ = 0 (т. е. являются нулями производной), а с другой — лежат на отрезке [0; 1]: x_{1}, x_{2} [0; 1]
- На этом шаге допускается больше всего ошибок: мы подставляем в исходную функцию сначала концы отрезка — f(0), f(1) — а затем в эту же функцию подставляем нули производной — находим значения f(x_{1}), f(x_{2}).
Практика показывает, что, как правило, мы получаем только один корень. В этом корне как раз и возникает ответ ко всей задаче, т. е. наименьшее или наибольшее значение функции, но бывают исключения, поэтому концы отрезка тоже нужно подставлять.
Помните: далеко не всегда наибольшее или наименьшее значение функции достигается в точках максимума или минимума. Вполне возможно, что наибольшее или наименьшее значение возникнет на концах отрезка.
Решение задачи B15 по алгоритму
Давайте применим этот четырехступенчатый алгоритм к нашей функции:
Шаг 1: Считаем производную функции
Поскольку перед нами дробь, то сейчас нужно будет считать производную дроби. Напомню, что производная частного считается по следующей формуле:
Применяем это правило для нашей функции. Считаем производную:
Разбираемся с числителем. Первая мысль, которая возникает — раскрыть все скобки и привести слагаемые. Но это не самый оптимальный вариант, потому что есть более красивый и быстрый путь. Давайте заметим: первая скобка — (−1 + 2х), а последняя скобка — (1 − 2х), т. е. эти скобки противоположны друг другу. С помощью минуса мы можем поменять знаки. Смотрите:
Теперь мы видим, что в первом и во втором слагаемом есть общий множитель, а именно — (−1 + 2х). Давайте вынесем этот общий множитель за скобку:
Готово! Производная частного найдена.
Шаг 2: Приравниваем производную к нулю и решаем уравнение
Мы получили довольно простую конструкцию, которая является нашей производной. Переходим ко второму шагу: приравниваем эту конструкцию к нулю и считаем корни:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Множитель «2» в этом случае не может быть равен нулю, поэтому:
−1 + 2x = 0;
x = 1/2.
Разумеется, при таком х знаменатель будет отличен от нуля, потому что при подстановке у нас получится 5/4, что явно не является нулем. Следовательно, x = 1/2 является единственным корнем (когда производная равна нулю).
Шаг 3: Отбор корней на отрезке
Переходим к третьему шагу: отбираем корни, лежащие на отрезке [0; 1]. В нашем случае корень 1/2 действительно принадлежит этому отрезку:
1/2 ∈ [0; 1]
Следовательно, мы смело можем переходить к четвертому шагу и подставлять все три числа, а именно — корень 1/2 и концы отрезка 0 и 1 — в исходную функцию:
Шаг 4: Подстановка значений переменной в исходную функцию
Давайте подставлять. Начнем с самого сложного — числа x = 1/2. Считаем:
Теперь подставляем x = 0:
Наконец подставляем х = 1, т. е. правый конец отрезка:
У нас получилось то же самое число.
Вычисление наибольшего значения функции на отрезке
Итого у нас получилось три значения функции, т. е. три кандидата на ответ. На самом деле их два, потому что два последних совпадают. Получаем два числа: y = 0,6 и y = 1.
Давайте вернемся к исходному условию задачи, посмотрим, что от нас требуется. А от нас требуется найти наименьшее значение функции. Т. е. из двух полученных чисел — 0,6 и 1 — нужно выбрать наименьшее. Очевидно, что ответом будет y = 0,6. Все, задача решена.
Важное замечание о наибольшем и наименьшем значении функции
Единственный момент, на который я бы хотел обратить ваше внимание, заключается в следующем. Давайте еще раз вернемся к нашему алгоритму:
- Найти производную: f’;
- Решить уравнение: f’ = 0;
- Отобрать корни на отрезке: x_{1}, x_{2} ∈ [0; 1];
- Вычислить значение функции в оставшихся нулях производной и на концах отрезка: f(0); f(1); f(x_{1}); f(x_{2}).
На четвертом пункте мы считаем значение функции не только в нулях производной, но еще и на концах отрезка. У многих учеников возникнет вопрос: зачем вообще считать значение функции на концах отрезка, если и так ясно, что наибольшее или наименьшее значение принимается в нулях производной?
Хочу вас предупредить: это очень частое и ошибочное заблуждение! Потому что при наличии любых ограничений отнюдь не всегда наибольшее или наименьшее значение функции достигается в точке максимума или минимума.
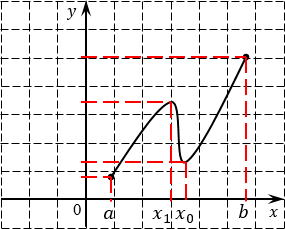
Рассмотрим простой пример. Взгляните на такую функцию:
Ну и где достигается наибольшее и наименьшее значение этой функции, а где — точки максимума и минимума? Точка минимума очевидна — назовем ее x0. В ней убывание функции сменяется возрастанием. И напротив, точка x1 является точкой максимума, потому что в ней возрастание функции сменяется убыванием.
Однако максимальное значение функции достигается отнюдь не в точке x = x1, а на конце отрезка — именно в точке x = b функция поднимается на максимальную высоту. И наоборот: наименьшее значение достигается именно в точке x = a, а никак не в точке минимума x = x0. Поэтому помните: наибольшее и наименьшее значение функции на отрезке совсем необязательно достигается в точках максимума и минимума. Это значение также может достигаться на концах отрезка.
Далеко не всегда наибольшее или наименьшее значение функции достигается в точке экстремума! Очень часто это происходит на концах отрезка.
Применительно к задачам из ЕГЭ по математике можно сказать следующее: такие графики функций, когда наибольшее значение оказывается на концах отрезка, в настоящих задачах из ЕГЭ встречаются крайне редко. Однако они все-таки существуют, в том числе в настоящем ЕГЭ, а не только в пробниках. Поэтому будет очень обидно, если, зная, как решается задача, вы, тем не менее, допустите в ней ошибку — просто потому, что не проверите концы отрезка.
Удачи вам в подготовке к ЕГЭ по математике, оставайтесь с нами, решайте задачи, смотрите видеоуроки — и никакие (даже самые сложные!) задачи по математике вам будут не страшны. А у меня на сегодня все.:)
Смотрите также:
- B15: Линейные функции и производная частного
- Задача B15 — исследование функции с помощью производной
- Решение ЕГЭ-2011: вариант 1, часть B
- Тест: простейшие показательные уравнения (2 вариант)
- Формулы приведения: ускоряем вычисления в тригонометрии
- ЕГЭ 2022, задание 6. Касательная к графику функции
Содержание:
Прямая:
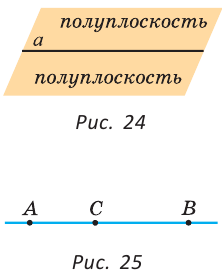
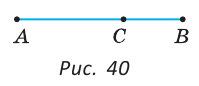
Прямая бесконечна (в обе стороны) и разбивает плоскость на две полуплоскости (рис. 24), для которых прямая является границей. Граница принадлежит полуплоскостям. На рисунке 25 точка С лежит на прямой между точками А и В, которые лежат по разные стороны от точки С. Точки С и В лежат по одну сторону от точки А. Из трех точек на прямой одна и только одна точка лежит между двумя другими.
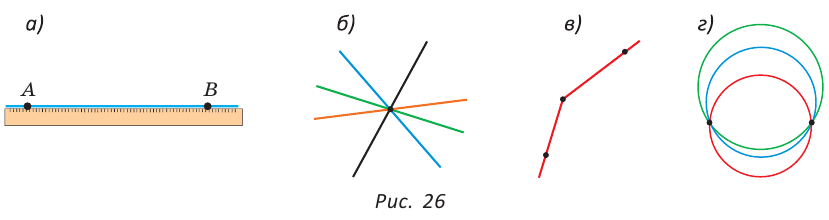
Если на плоскости отметить две точки А и В, то через них всегда можно провести прямую АВ (рис. 26, а). Через одну точку можно провести бесконечно много прямых (рис. 26, б), через три точки не всегда можно провести прямую (рис. 26, в). Через две точки можно провести бесконечно много окружностей (рис. 26, г), а прямую — только одну!
Аксиома прямой. Через любые две точки плоскости можно провести прямую, и притом только одну.
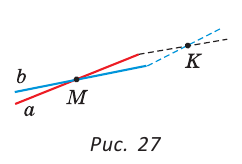
Из аксиомы следует, что если две прямые (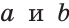
Определение. Две прямые называются пересекающимися, если они имеют общую точку.
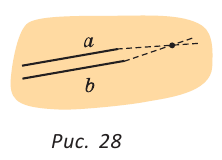
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если прямые 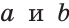
Луч:
Определение. Лучом называется часть прямой, ограниченная одной точкой.
Точка, ограничивающая луч, принадлежит лучу и называется началом луча. Луч бесконечен (в одну сторону). Он обозначается одной малой буквой, или двумя большими буквами, где первой всегда записывается начало луча.
При этом вторая точка может быть не отмечена на луче. Она указывает направление луча, например как точка В на луче АВ (рис. 29).
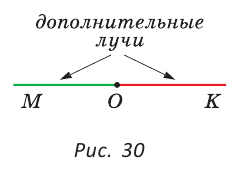
Определение. Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой.
На рисунке 30 изображены дополнительные дополнительные лучи ОМ и ОК. Они дополняют друг друга до прямой. Чтобы построить луч, дополнительный данному, достаточно продлить данный луч за его начало вдоль прямой, на которой лежит данный луч. Любая точка прямой разбивает ее на два дополнительных луча.
Отрезок:
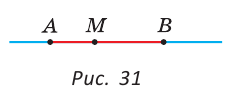
Определение. Отрезком называется часть прямой, ограниченная двумя точками.
Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. На рисунке 31 изображен отрезок АВ с концами А и В. Точка М — внутренняя точка отрезка АВ.
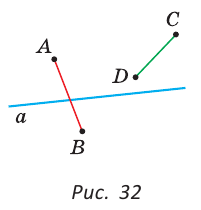
Если концы отрезка лежат в разных полуплоскостях относительно прямой, то этот отрезок пересекает прямую, если в одной полуплоскости — то не пересекает. На рисунке 32 концы отрезка АВ лежат в разных полуплоскостях относительно прямой а, и он пересекает прямую 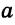
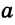
Если при наложении отрезков их концы совпадут, то по аксиоме прямой эти отрезки совпадут всеми своими точками.
Определение. Два отрезка называются равными, если их можно совместить наложением.
Важной характеристикой отрезка является его длина.
Свойства длины отрезка: каждый отрезок имеет длину, выраженную положительным числом; равным отрезкам соответствуют равные длины, большему отрезку — большая длина. И наоборот.
Аксиома измерения отрезков. Если на отрезке взять точку, то она разобьет данный отрезок на два отрезка, сумма длин которых равна длине данного отрезка.
Аксиома откладывания отрезков. На любом луче от его вершины можно отложить отрезок данной длины, и притом только один.
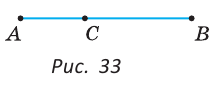
На рисунке 33 точка С лежит на отрезке АВ. По аксиоме измерения отрезков следует, что АС + СВ=АВ.
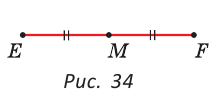
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке 34 точка М — середина отрезка EF, то есть ЕМ = MF.
Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
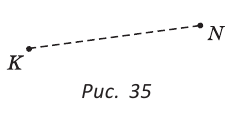
На рисунке 35 расстояние между точками К и N равно длине отрезка KN.
Ломаная:
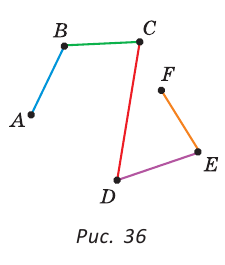
На рисунке 36 отрезки АВ, ВС, CD, DE и EF последовательно соединены своими концами: отрезок ВС соединен с отрезком АВ, отрезок CD соединен с отрезком ВС и так далее. Полученная фигура представляет собой ломаную ABCDEF. Указанные отрезки называются звеньями ломаной, а точки А, В, С, D, Е и F — вершинами ломаной.
Определение. Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами, у которой никакие два соседних звена не лежат на одной прямой. Длиной ломаной называется сумма длин ее звеньев.
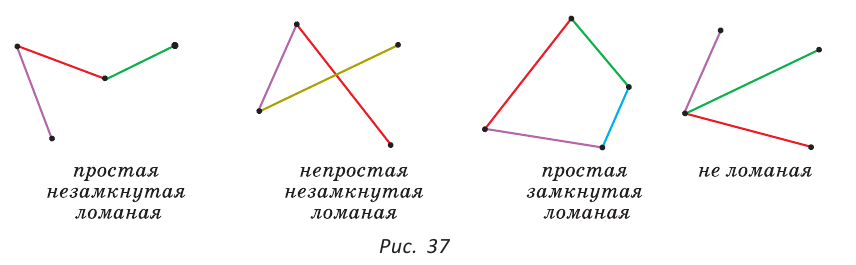
Определение. Ломаная называется замкнутой, если начало ее первого звена совпадает с концом последнего. В противном случае она называется незамкнутой. Ломаная называется простой, если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек. В противном случае она называется непростой (рис. 37).
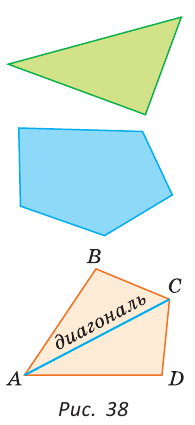
Простая замкнутая ломаная на плоскости называется многоугольником. Звенья этой ломаной называются сторонами этого многоугольника, а вершины — вершинами многоугольника. Периметром многоугольника называется сумма длин его сторон. Часть плоскости, ограниченная многоугольником, называется плоским многоугольником. Слово «плоский» употреблять не будем. Отрезок, соединяющий вершины многоугольника, не принадлежащие одной стороне, называется его диагональю. Если у многоугольника три стороны, то у него три вершины и три угла, и он называется треугольником, если четыре стороны — четырехугольником, если пять — пятиугольником и так далее.
На рисунке 38 изображен четырехугольник ABCD со сторонами АВ, ВС, CD и AD. У него четыре угла: 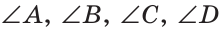
При записи многоугольника его вершины записываются последовательно, начиная с любой вершины и в любом направлении. Например, СBAD — это тот же четырехугольник ABCD.
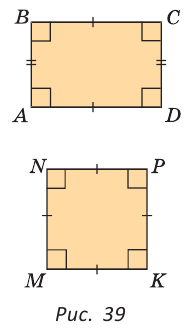
Самые известные четырехугольники — это прямоугольник и квадрат. У прямоугольника все углы прямые, а противоположные стороны равны. Квадрат — это прямоугольник, у которого все стороны равны. На рисунке 39 ABCD — прямоугольник, MNPK — квадрат. Позже мы дадим определение прямоугольника и квадрата и рассмотрим их свойства подробно. А пока будем пользоваться указанными представлениями.
Пример:
На отрезке АВ, равном 24 см, взята точка С. Отрезок АС на 6 см больше отрезка СВ. Найти длину отрезка АС.
Решение:
Пусть СВ = 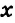
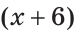
По аксиоме измерения отрезков 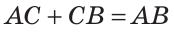
То есть,
Ответ: 15 см.
Замечание. В дальнейшем при решении задач не будем ссылаться на аксиому измерения отрезков.
Пример:
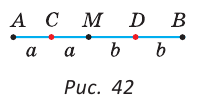
На отрезке АВ отмечены точки С и D (рис. 41). Найти длину отрезка CD, если:
Решение:
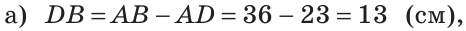
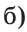
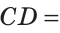
Ответ: а) 6 см; б)
Пример:
На отрезке АВ, равном 42 см, взята точка М. Найти расстояние между серединами отрезков AM и MB.
Решение:
Пусть С — середина отрезка AM, D — середина отрезка MB.
Обозначим 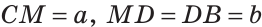
Тогда
Следовательно, 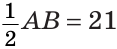
Ответ: 21 см.
Замечание. В данной задаче мы доказали свойство: «Если на отрезке отмечена точка, то расстояние между серединами полученных отрезков равно половине данного отрезка». Утверждения, которые будут доказаны нами в ключевых задачах, могут в дальнейшем использоваться как известные свойства.
Прямая в высшей математике
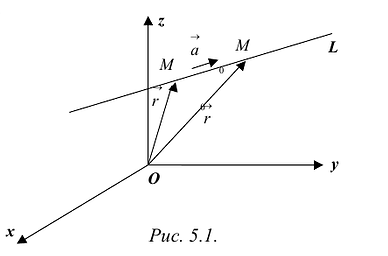
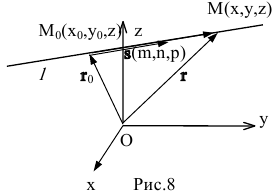
Прямая L в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой). Пусть задана такая точка 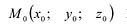
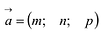
Если М(х, у, z) — произвольная текущая точка прямой L, то вектор 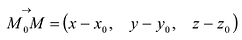
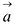
Этим соотношениям удовлетворяют координаты любой точки прямой L и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 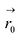
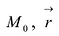
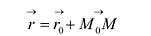
В силу коллинеарности векторов 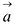
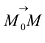
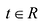
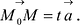
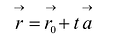
В координатной форме уравнение (5.3) равносильно трем уравнениям:
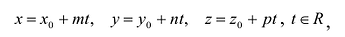
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (5.4) параметр t, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к t. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 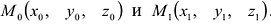
Очевидно, что в этом случае направляющим вектором прямой L будет вектор 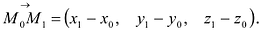
Прямую L в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии L в общем виде:
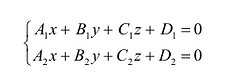
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы 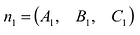
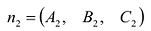
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку 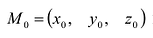
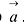
Точку 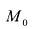
Направляющий вектор 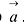
Поэтому в качестве 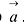
- Заказать решение задач по высшей математике
Понятие прямой
Нормальным вектором прямой называется любой вектор, перпендикулярный прямой.
Направляющим вектором прямой называется любой вектор, лежащий на этой прямой.
Взаимное расположение прямых
Пусть даны две прямые:
Эти прямые заданы своими точками 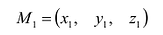
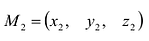
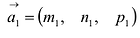
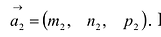
Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямых можно записать в виде:
Условие параллельности:
Возможны четыре случая взаимного расположения прямых:
Условие (5.8) выполняется в случаях I-III и означает, что прямые лежат в одной плоскости.
Уравнения прямой на плоскости
1. Па плоскости Оху составим уравнение прямой l, проходящей через точку 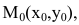
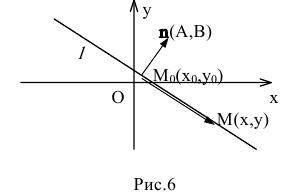
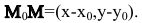
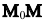
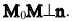
В координатной форме это равенство примет вид:
Уравнение Ах+Ву+С=0, где А и В не равны одновременно нулю 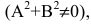
Если 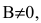
притом 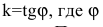
Вывод. Прямая на плоскости однозначно определяется точкой и нормальным вектором.
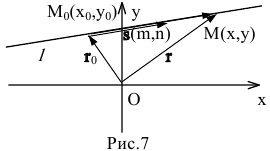
2. Па плоскости Оху составим уравнение прямой l, проходящей через точку 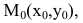
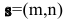
Пусть М(х,у) — произвольная точка прямой l, 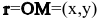
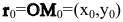
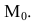
Так как векторы 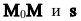
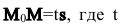
или в координатной форме параметрические уравнения прямой:
Пусть m и n отличны от нуля. Разрешим каждое из уравнений относительно t:
откуда получаем каноническое уравнение прямой:
Пусть прямая l проходит через две точки 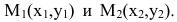
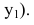
Вывод. Прямая однозначно определяется точкой и направляющим вектором.
Пример:
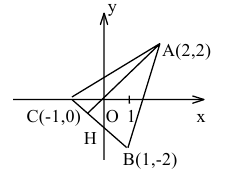
Вершины треугольника находятся в точках А(2,2), В(1,-2), С(-1,0). Найти проекцию точки А на основание ВС.
Решение:
Построим чертеж.
Проекция точки А на ВС есть точка пересечения основания ВС с перпендикуляром, опущенным из А на ВС.
Составим уравнение прямой ВС по двум точкам:
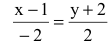
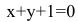
Обозначим искомую проекцию точкой Н(х,у). Т.к. 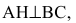
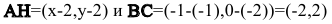
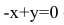
Теперь найдем проекцию точки А на основание ВС. Для этого решим систему: 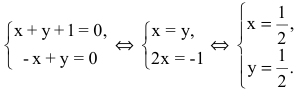
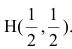
Замечание. Уравнение прямой АН можно было находить другими способами. Например, из общего уравнения прямой ВС х+у+1=0 можно выписать координаты нормального вектора 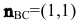
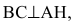
По нормальному вектору 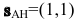
Уравнения прямой в пространстве
Уравнения прямой l, проходящей через точку 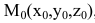
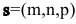
Пусть M(x,y,z) — произвольная точка прямой 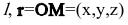
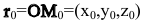
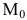
Тогда векторное уравнение прямой останется прежним: 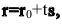
Параметрические уравнения прямой примут вид:
В случае 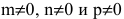
Наконец, составим уравнения прямой, проходящей через две точки
Внимание! В пространстве точка и нормальный вектор однозначным образом определяют плоскость. Поэтому в пространстве общие уравнения прямой будут задаваться линией пересечения двух плоскостей.