Преобразовать уравнение как пишется

Иногда работа с документами в Microsoft Word выходит за пределы обычного написания текста, и может потребоваться, например, записать простое математическое выражение или просто числа, представляющие собой дроби. О том, как это можно делать, расскажем в рамках настоящей статьи.

Написание дробей в Ворде

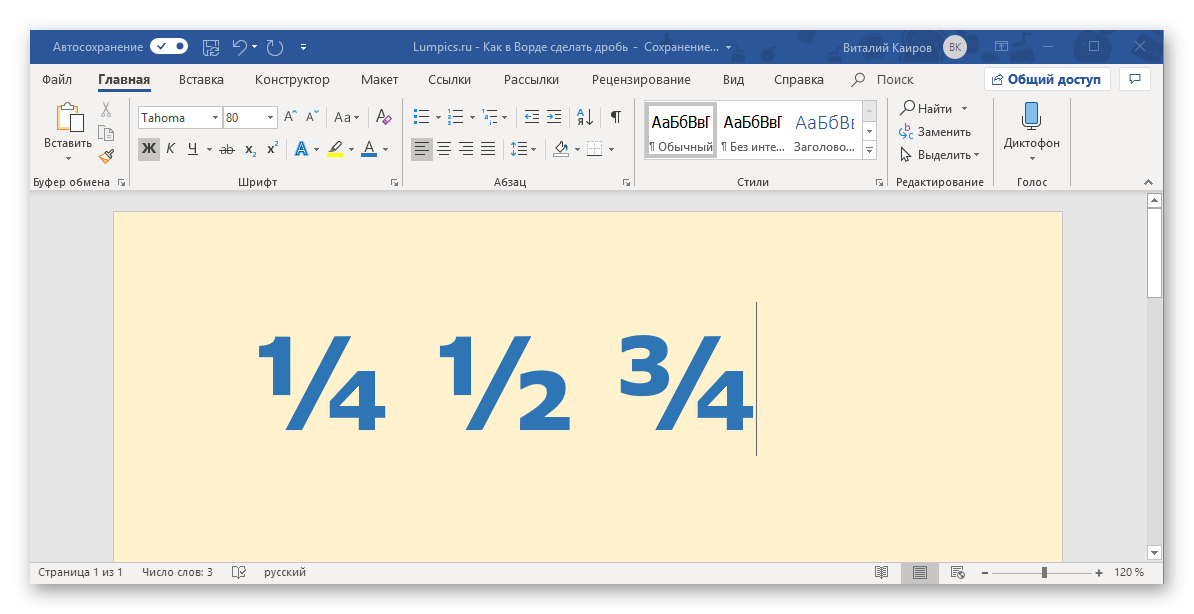
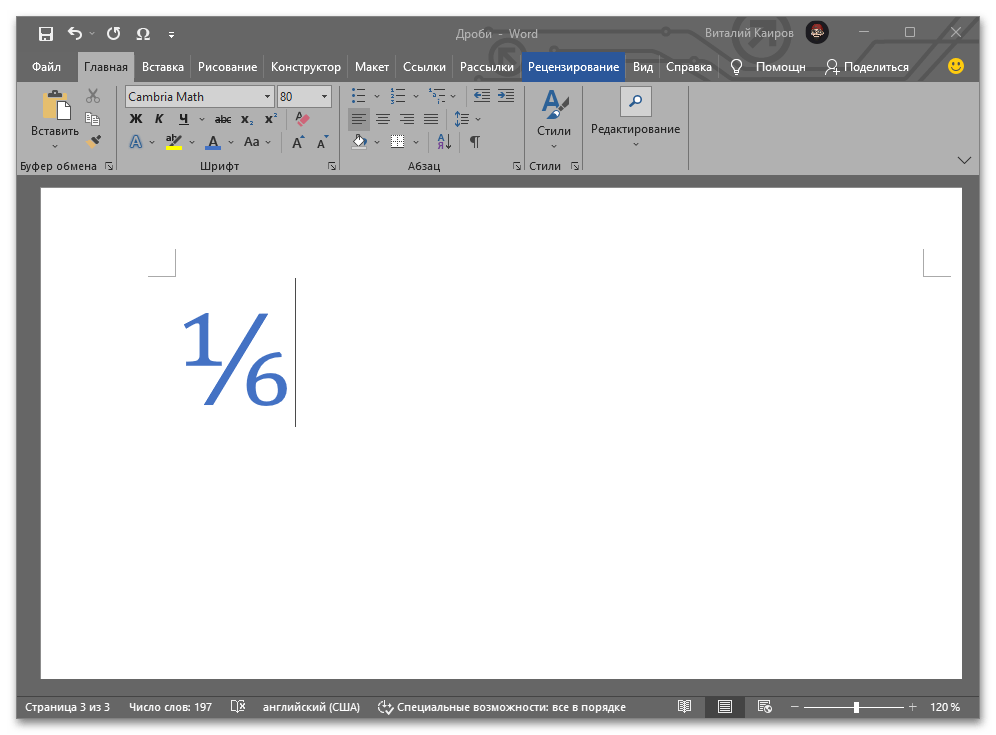
Определенные дроби, введенные вручную, автоматически заменяются в Word на те, которые можно смело назвать правильно написанными. К таковым относятся 1/4, 1/2, 3/4 — после автозамены они приобретают вид ¼, ½, ¾. Однако такие дроби, как 1/3, 2/3, 1/5 и им подобные не заменяются, поэтому должный вид им необходимо придавать вручную.

Стоит отметить, что для написания вышеописанных дробей используется символ «слеш» — / — косую черту, но ведь всех нас еще в школе приучили к тому, что правильное написание дробей — это одно число, расположенное под другим, а разделителем в таком случае выступает горизонтальная линия. Далее мы более подробно рассмотрим каждый из доступных вариантов написания дробей в Ворде.

Вариант 1: Автозамена

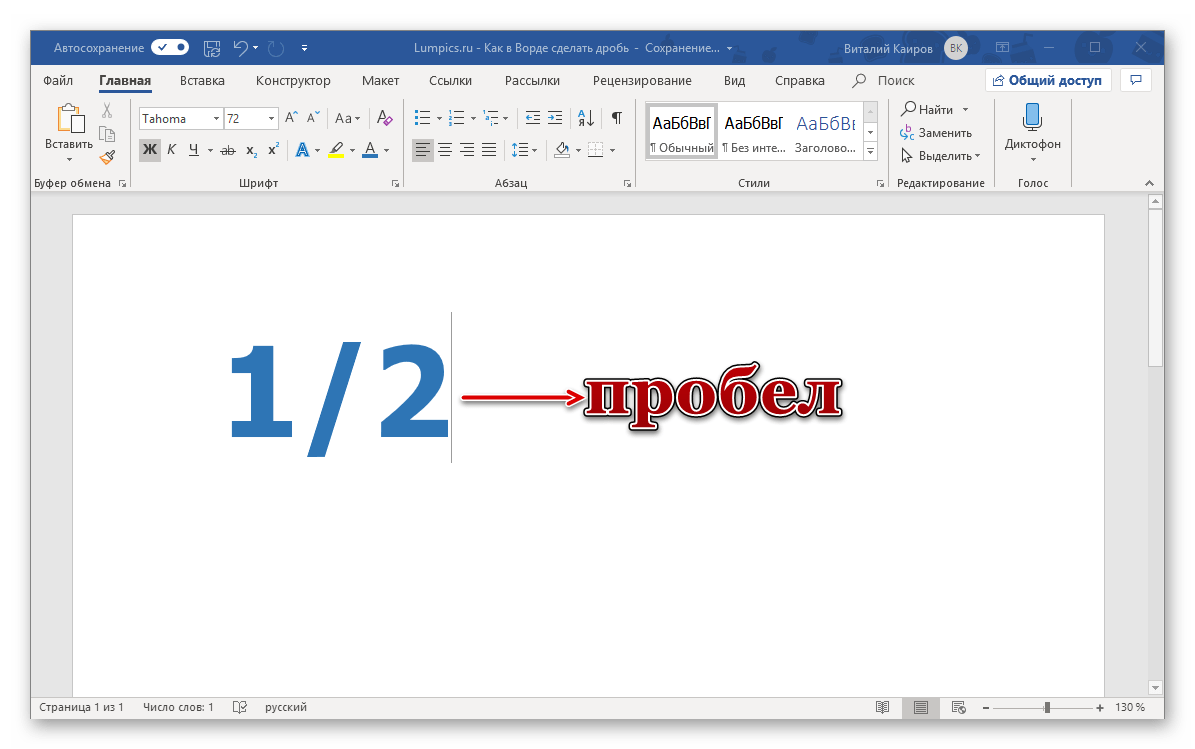
Как мы уже сказали во вступлении, некоторые дроби, записанные через «слеш», Word автоматически заменяет на правильные. То есть все, что от вас требуется в данном случае – написать выражение, а затем нажать на пробел, после чего произойдет автозамена.

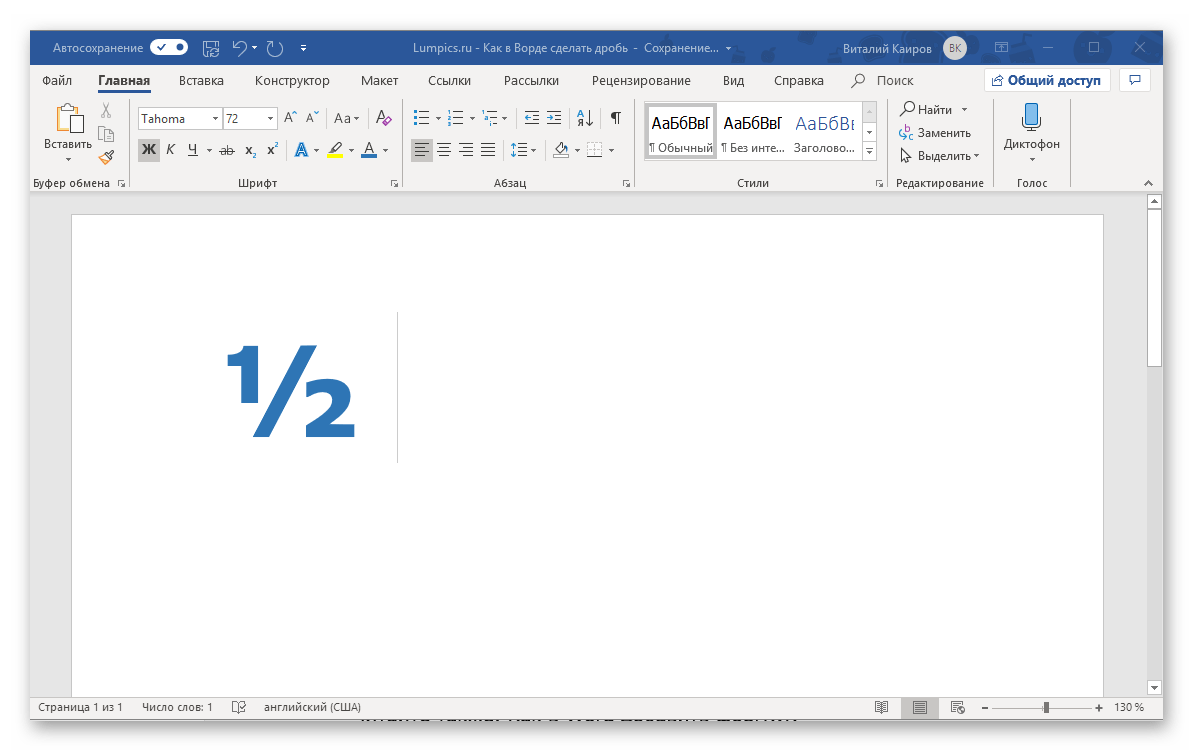
Пример. Пишем 1/2, после чего нажимаем пробел и получаем ½.

Если вы знаете о функции автозамены в Microsoft Word и понимаете принцип ее работы, то наверняка уже догадались, что подобным образом можно настроить замену введенных с клавиатуры числовых символов на «правильные» дроби с разделителем в виде косой черты для всех дробей или хотя бы наиболее часто используемых. Правда, для этого придется обзавестись «источником» этих самых «правильных» записей (расширенный, но все же неполный набор таких символов представлен в Способе 2 части Вариант 2 настоящей статьи).

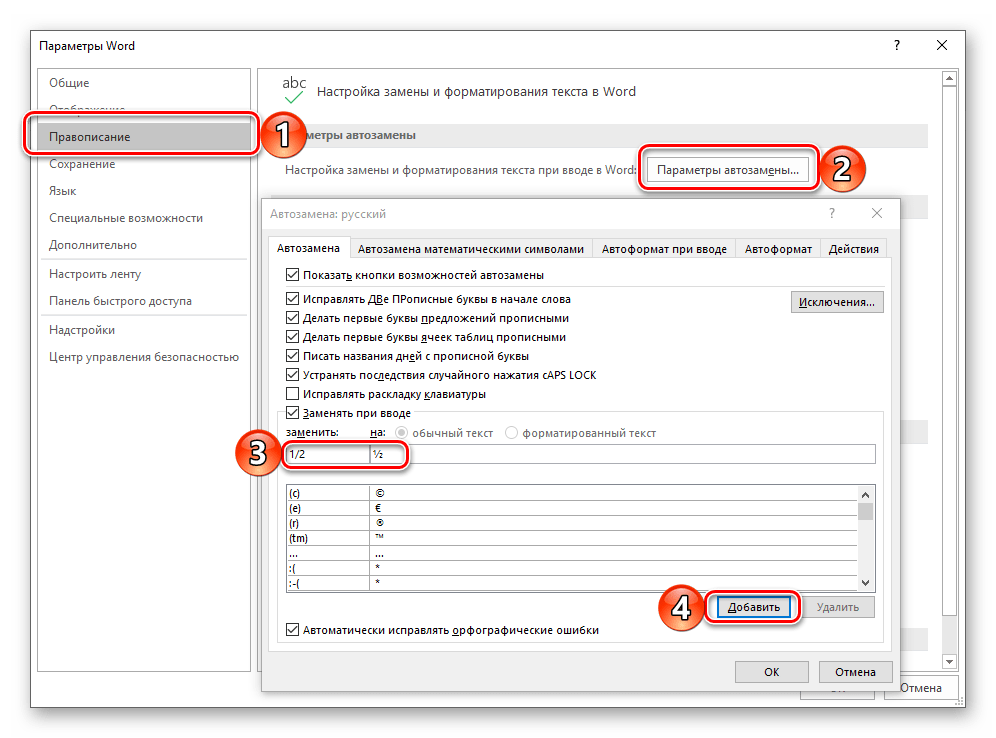
Настроить автоматическую замену можно в разделе «Параметров» текстового редактора. Открыв их, перейдите на боковой панели во вкладку «Правописание» и нажмите по кнопке «Параметры автозамены». В появившемся диалоговом окне в поле «заменить» введите дробь в обычном написании, а в соседнее поле «на» вставьте ее «правильное» написание, после чего воспользуйтесь кнопкой «Добавить». Аналогичное проделайте со всеми остальными дробными выражениями, которые планируете использовать в дальнейшем. Узнать же более подробно о том, что представляет собой автозамена в Ворде, как пользоваться данной функцией и как настроить ее работу под себя, можно в представленной по ссылке ниже статье.

Подробнее: Работа функции «Автозамена» в Word

Вариант 2: Дробь со слешем

Ввести дробь такого вида можно одним из двух методов – посредством вставки доступных в стандартном наборе Ворда символов или использованием соответствующих им кодовых выражений и дополнительных сочетаний клавиш.

Способ 1: Вставка символа

В базовом арсенале Microsoft Word содержится всего шесть знаков дробей со слеш-разделителем. Их добавление осуществляется по следующему алгоритму:

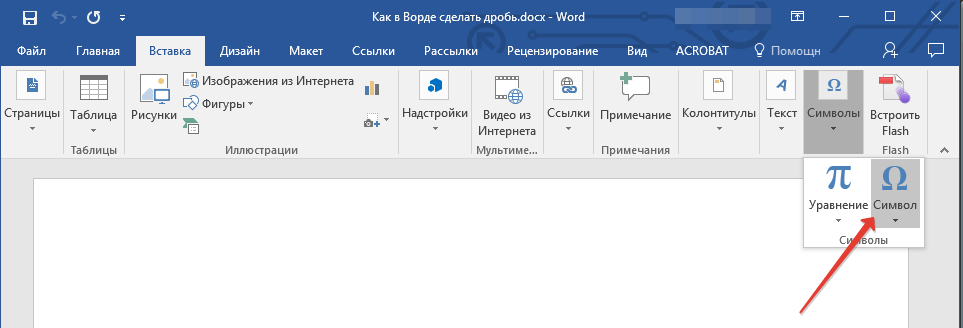
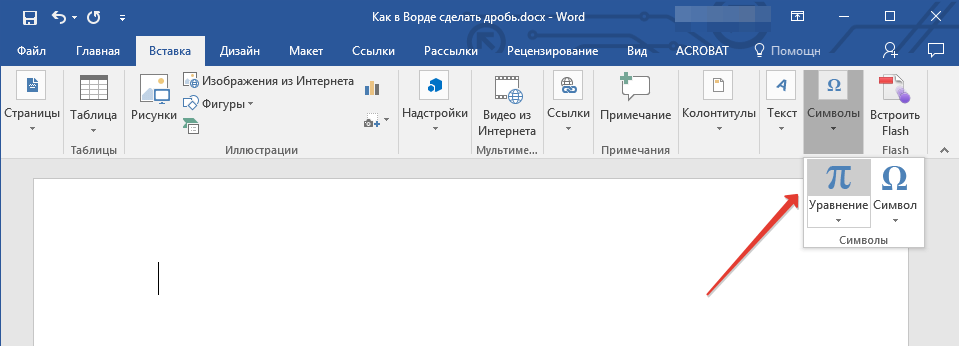
1. Откройте вкладку “Вставка”, нажмите на кнопку “Символы” и выберите там пункт “Символы”.



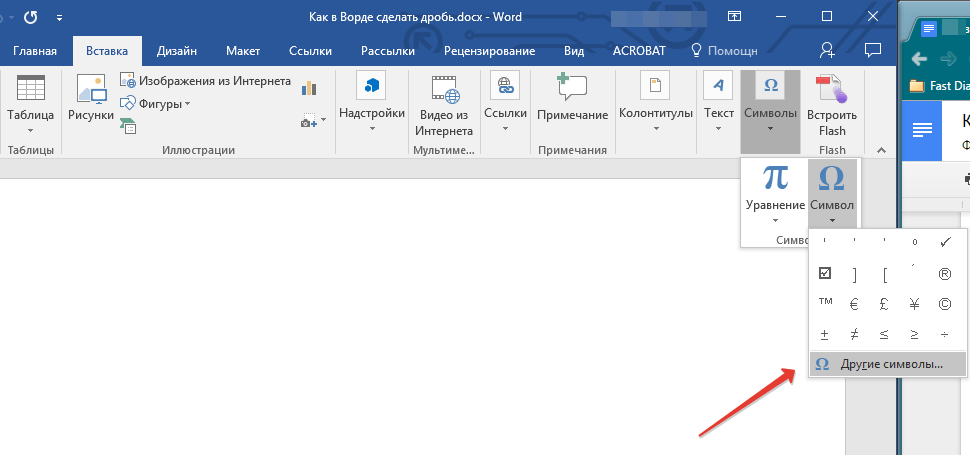
2. Нажмите на кнопку “Символ”, где выберите “Другие символы”.



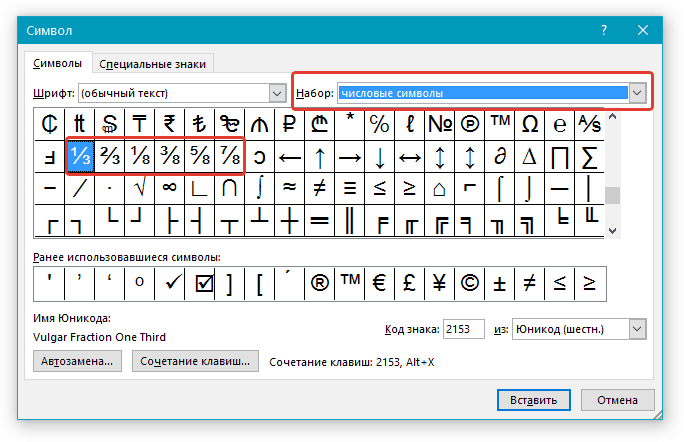
3. В окне “Символы” в разделе “Набор” выберите пункт “Числовые формы”.



4. Найдите там нужную дробь и кликните по ней. Нажмите кнопку “Вставить”, после чего можно закрыть диалоговое окно.
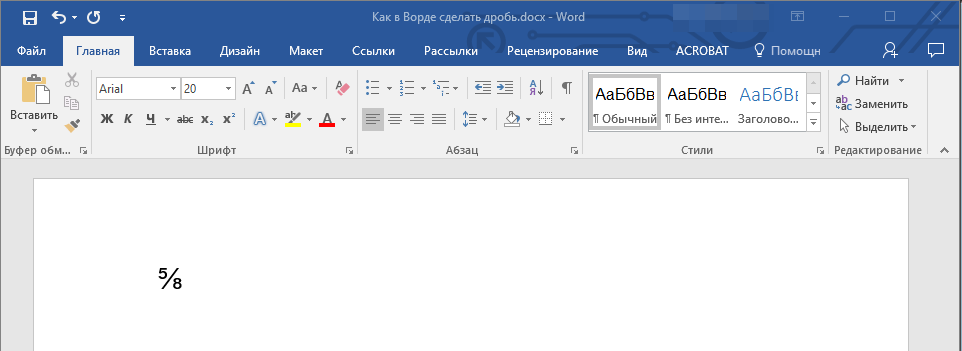
5. Выбранная вами дробь появится на листе.



К сожалению, набор шаблонных дробных символов в Ворд тоже весьма ограничен, а потому, если подобная запись должна быть именно с разделителем в виде слеша, оптимальным решением будет настройка функции автозамены, о которой мы рассказали выше, или иной вариации данного метода, о которой пойдет речь далее.

Читайте также: Как вставить галочку в MS Word

Способ 2: Код символа и горячие клавиши

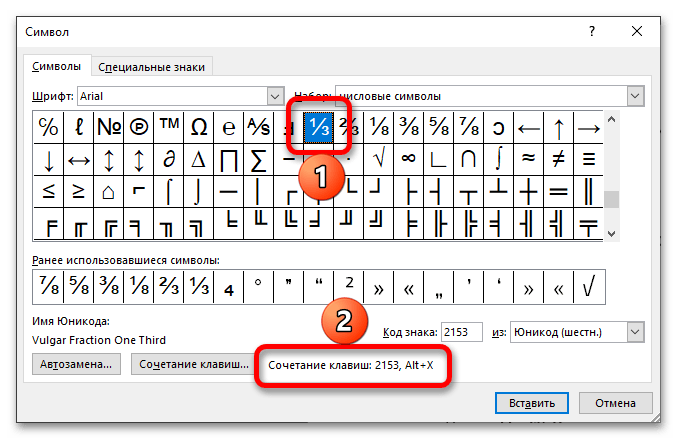
Каждый из доступных для вставки в Ворде символов имеет свой код, который можно преобразовать в необходимые знаки с помощью сочетания клавиш – узнать их можно при выделении соответствующего элемента в окне «Символ».

Так, показанные в предыдущей части статьи дроби, входящие в стандартный набор Microsoft Word, имеют следующие кодовые выражения:

⅓ — 2153
⅔ — 2154
⅛ — 215B
⅜ – 215C
⅝ – 215D
⅞ – 215E

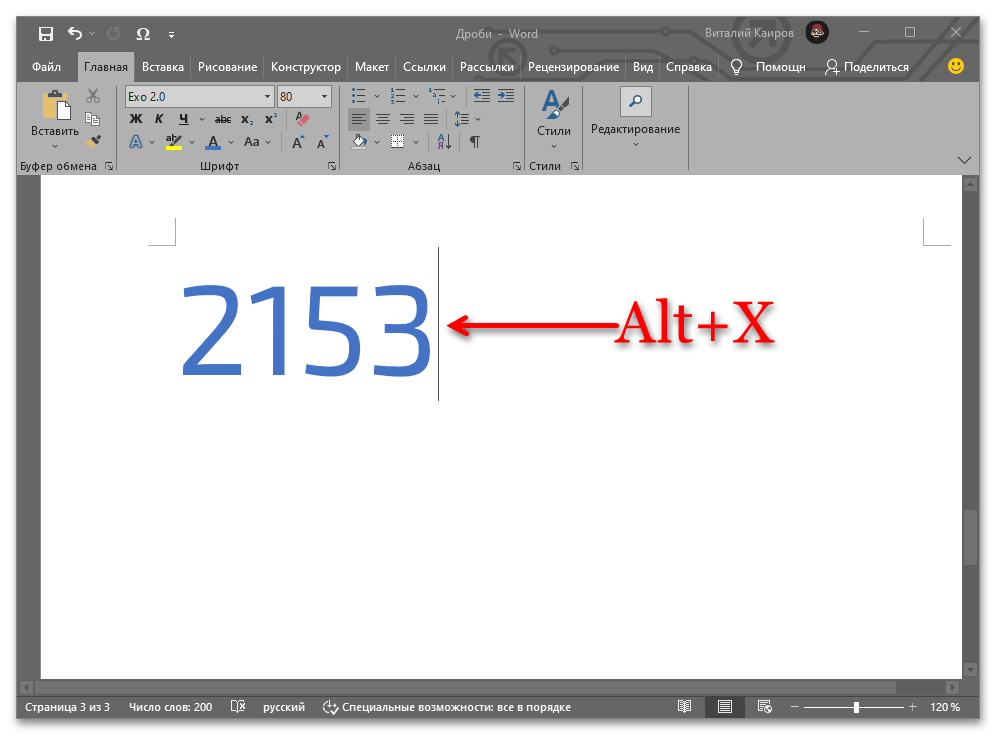
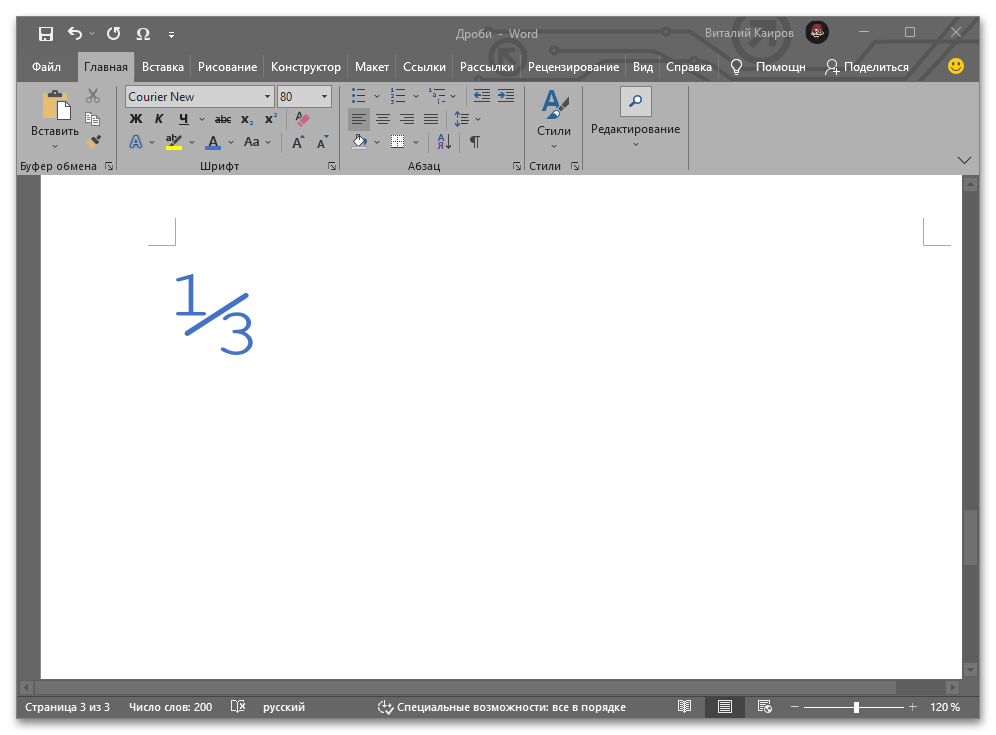
Введите необходимый набор цифр и/или цифр и букву, после чего, не делая отступа, воспользуйтесь клавишами «Alt+X» — код сразу же преобразуется в дробь со слешем.

Несмотря на то что в текстовом редакторе отсутствуют другие дробные знаки, некоторые из них все же можно вставить в документ. Ниже представлен расширенный набор кодовых выражений, преобразовать которые можно тем же сочетанием:

¼ — 00BC
½ – 00BD
¾ – 00BE
⅐ – 2150
⅑ – 2151
⅒ –2152
⅓ – 2153
⅔ – 2154
⅕ – 2155
⅖ – 2156
⅗ – 2157
⅘ – 2158
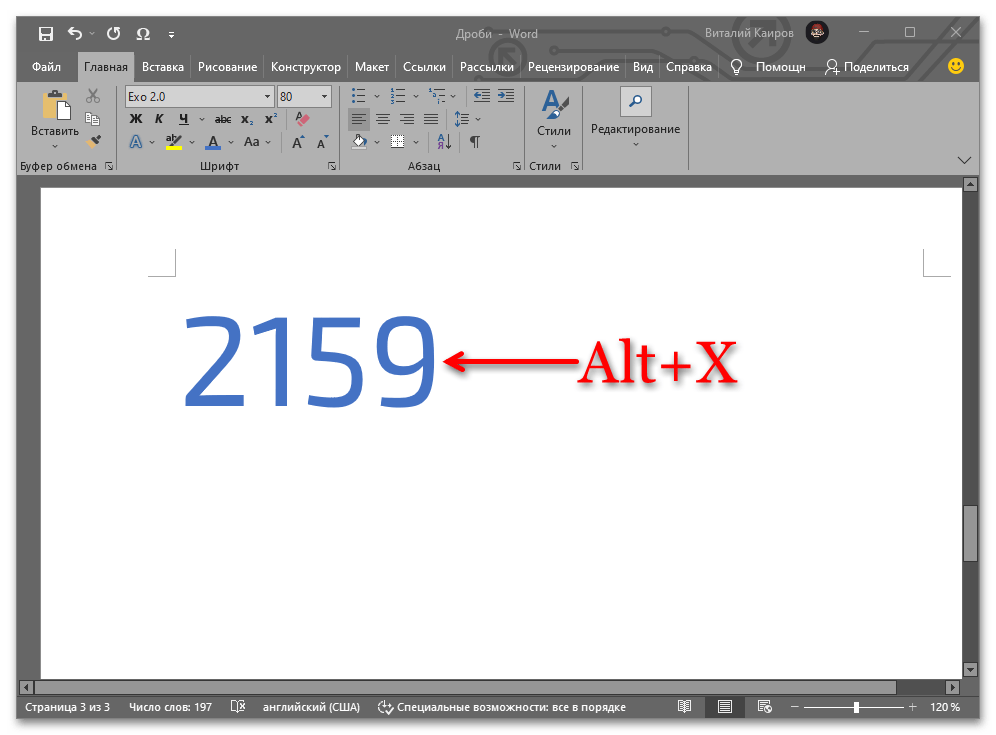
⅙ – 2159
⅚ – 215A
⅛ – 215B
⅜ – 215C
⅝ – 215D
⅞ – 215E
↉ – 2189

Аналогично вышесказанному, для получения любой из указанной выше дробей просто введите соответствующий ей код и затем нажмите «Alt+X».

Например, для получения записи ⅙ следует ввести и преобразовать комбинацией клавиш выражение 2159.

Вариант 3: Дробь с горизонтальным разделителем

Добавить в текстовый документ Ворд дробь с горизонтальным разделителем между числителем и знаменателем можно одним из двух методов – используя средства вставки уравнений или специальный код с его последующим преобразованием.

Способ 1: Вставка формулы

В Microsoft Word имеется набор инструментов для работы с математическими выражениями, для чего можно как использовать уже готовые формулы и уравнения (например, бином Ньютона или площадь круга), так и «собирать» их самостоятельно из более простых записей. В числе последних есть и интересующая нас в рамках настоящей статьи дробь с горизонтальным разделителем.

Читайте также: Как вставить формулу в Ворде

1. Откройте вкладку “Вставка” и выберите в группе “Символы” пункт “Уравнение”.

   

   Примечание: В старых версиях MS Word раздел “Уравнение” называется “Формулы”.

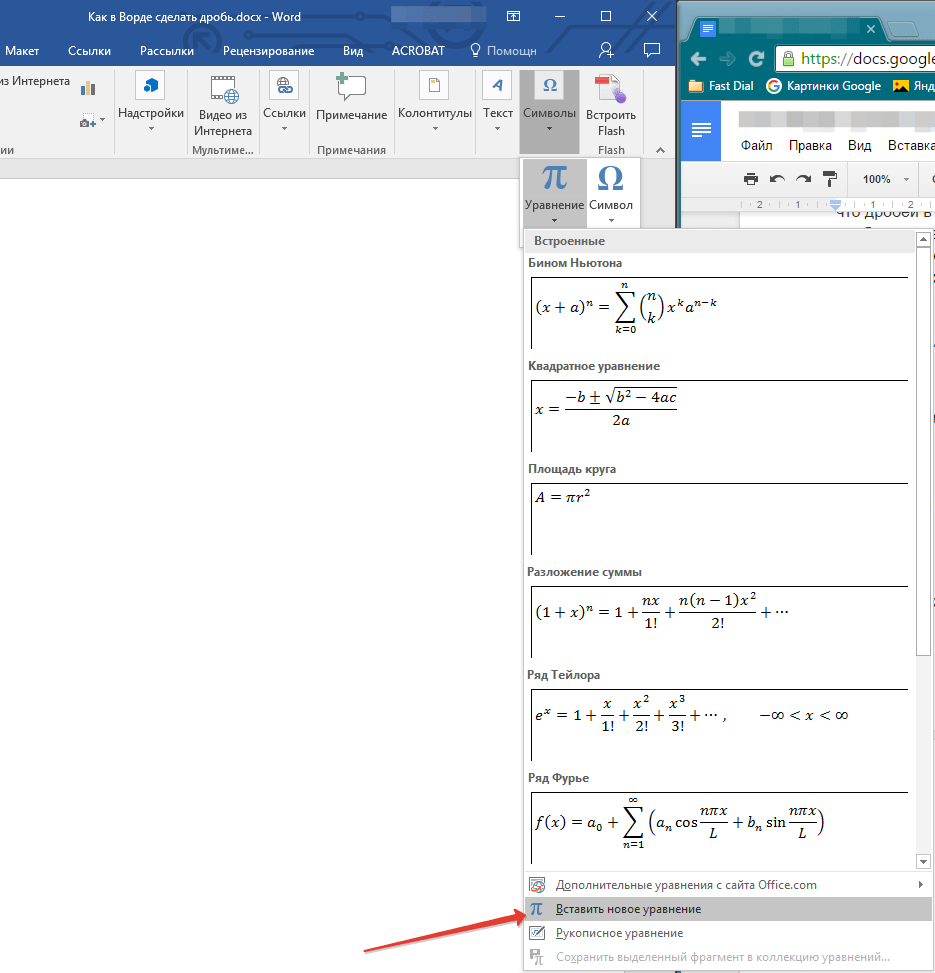
2. Нажав на кнопку “Уравнение”, выберите пункт “Вставить новое уравнение”.



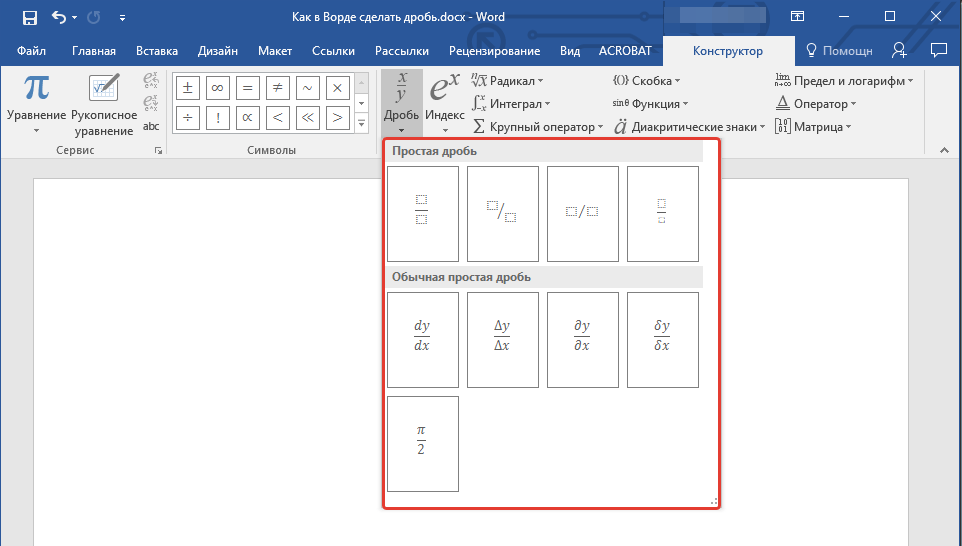
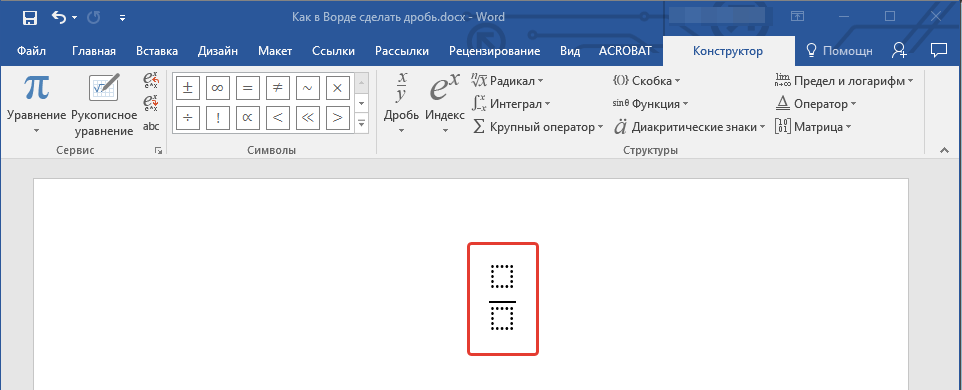
3. Во вкладке “Конструктор”, которая появится на панели управления, нажмите на кнопку “Дробь”.



4. В развернувшемся меню выберите в разделе “Простая дробь” тип дроби, которую вы хотите добавить — через слеш или горизонтальную линию.



5. Макет уравнения изменит свой внешний вид, впишите в пустые графы необходимые числовые значения.
6. Кликните по пустой области на листе, чтобы выйти из режима работы с уравнением/формулой.



Именно написание дроби через меню вставки нового уравнения является оптимальным решением нашей сегодняшней задачи, тем более, что таким образом можно добавлять выражения обоих типов — и те, что разделены слешем (косой чертой), и те, которые разделяются горизонтальной полосой. Особенно актуально использование этого метода в случае, когда одними дробями работа не ограничивается и требуется писать и другие математические выражения. Однако есть у такого подхода и недостаток — формулы и их компоненты представляют собой отдельные объекты, для которых доступны далеко не все варианты форматирования (например, нельзя изменить шрифт).

Читайте также: Как изменить шрифт в Word

Способ 2: Коды полей с ключами

Более простой в своей реализации альтернативой предыдущему решению является написание дробей с горизонтальным разделителем путем ввода и преобразования специального кода поля с ключом. Делается это следующим образом:

1. Установите указатель курсора в том месте текстового документа, где будет записана дробь.



2. Нажмите на клавиши «Ctrl+F9» (обратите внимание, что на ряде ноутбуков, где F-клавиши по умолчанию выполняют мультимедийные функции, дополнительно может потребоваться нажать клавишу «Fn», то есть сочетание в таком случае будет «Ctrl+Fn+F9»).



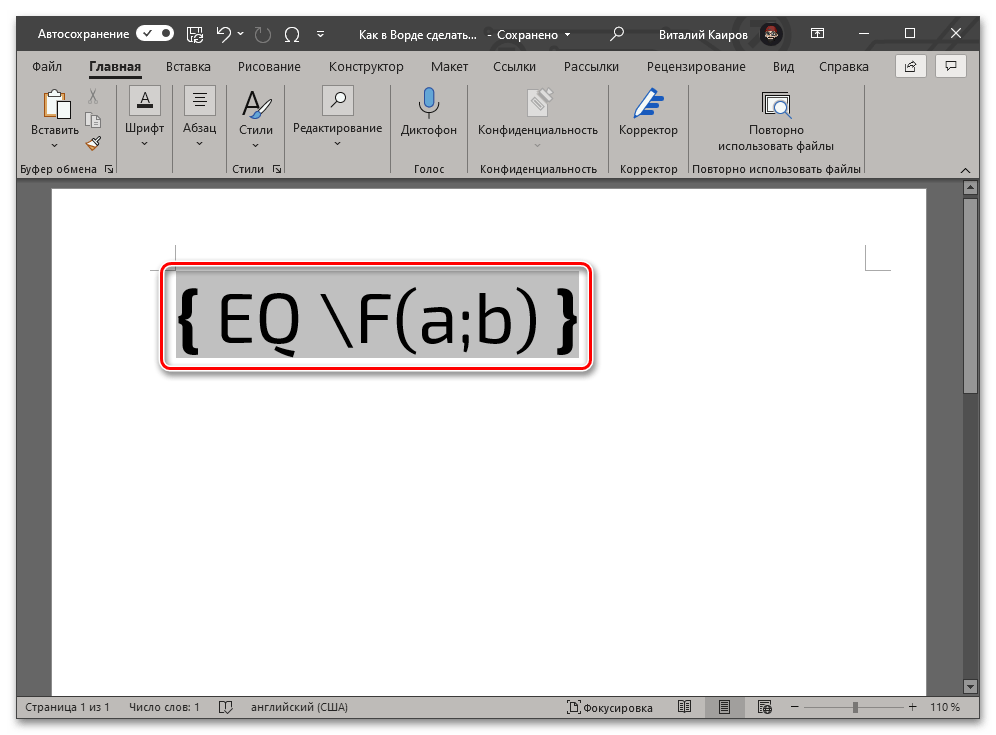
3. В выбранном месте документа появятся фигурные скобки с мигающей между ними кареткой (указатель курсора). Не перемещаясь из этой области, введите код следующего вида:

   EQ F(a;b)

   

   • EQ создает поле для ввода формулы;
   • F создает дробь с горизонтальным разделителем и выравнивает относительно этой линии числитель и знаменатель;
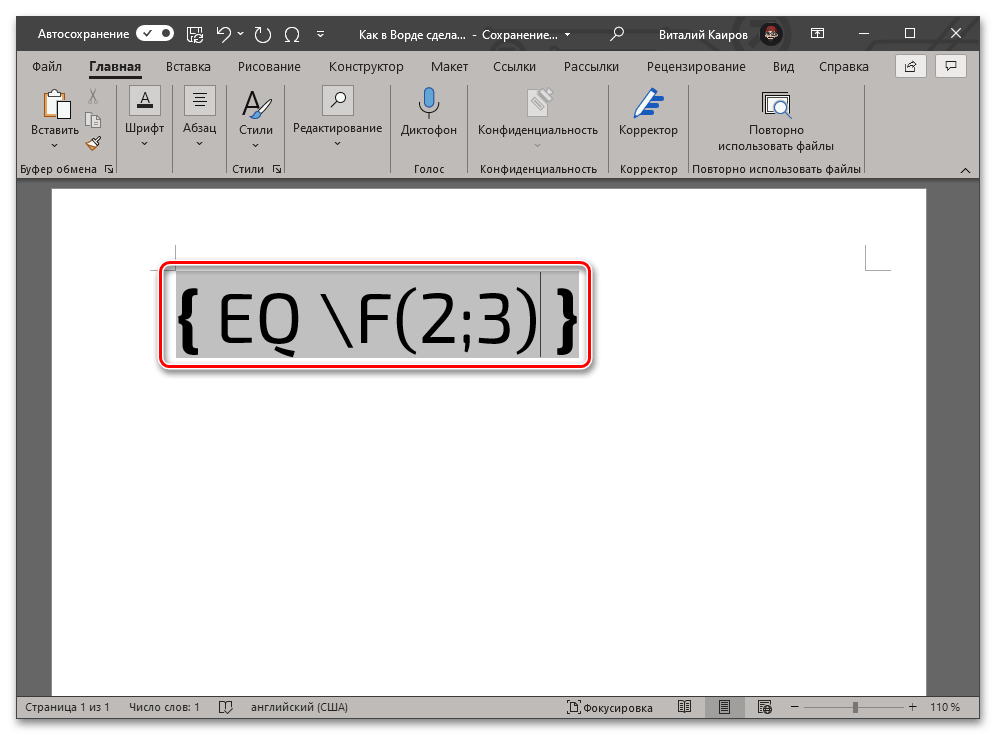
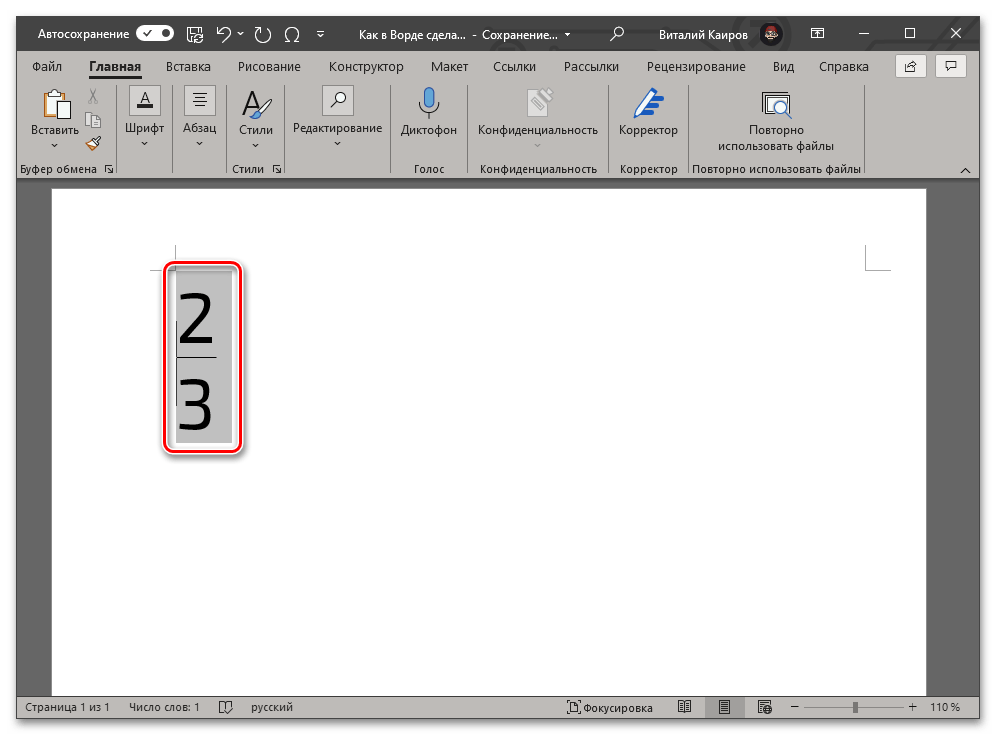
   • a и b – числитель и знаменатель, то есть вместо этих букв нужно вводить соответствующие им значения. Например, чтобы записать таким образом 2/3, следует использовать указанный ниже код:

   EQ F(2;3)

   

   Обратите внимание! В случае если вами используется локализованная версия операционной системы, а в качестве десятичного разделителя в ней выступает запятая, между числителем и знаменателем в скобках необходимо вводить точку с запятой, как это показано в примерах выше. То есть именно это решение применимо в абсолютном большинстве случаев. Однако если разделителем в ОС является точка (это характерно для англоязычных версий), между числителем и знаменателем потребуется ставить запятую.

4. Разобравшись со всеми параметрами кода и указав его в том виде, который соответствует желаемой дроби, не перемещая указатель курсора и не покидая обозначенное фигурными скобками поле для ввода, нажмите на клавишу «F9» (опять же, на ноутбуках может потребоваться нажать «Fn+F9»).

   

   Читайте также: Как поставить фигурные скобки в Майкрософт Ворд

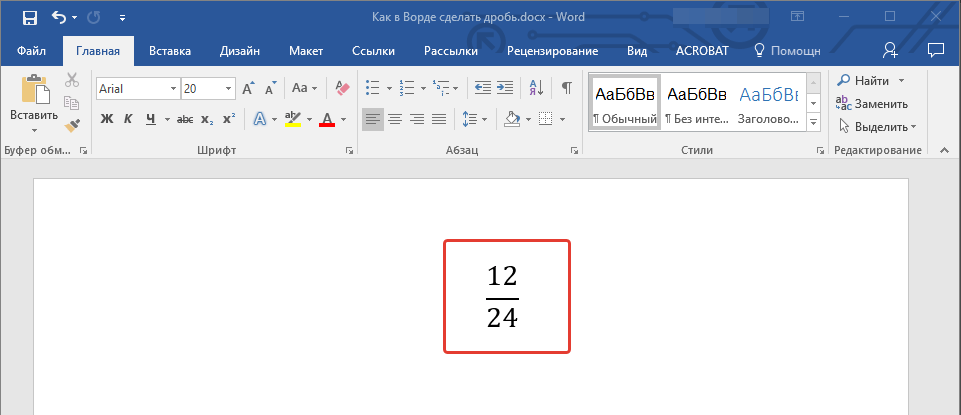
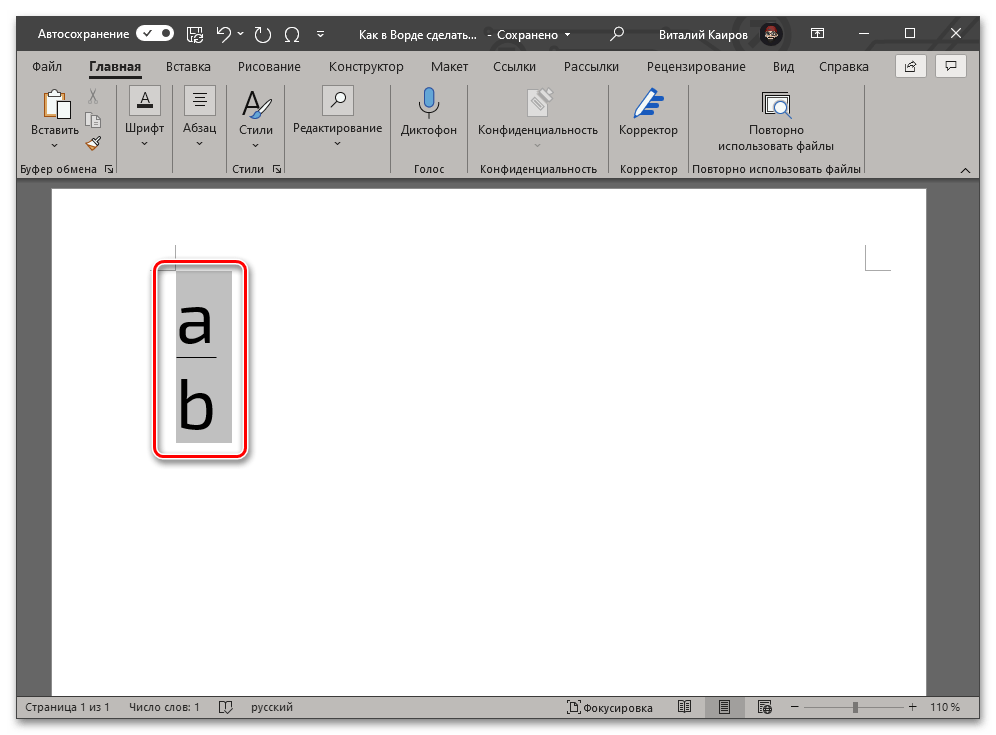
5. В результате выполнения предыдущего шага инструкции код будет преобразован в дробь с горизонтальным разделителем между числителем и знаменателем, что показано на представленных выше и ниже изображениях.



Этот метод является не только более простым и удобным в своем реализации, чем предыдущий, но и лишен характерных для него ограничений. Так, у записанной дроби отсутствует видимое поле (рамка), она выглядит более эстетично и является пригодной для общего форматирования, представляется в виде используемого по умолчанию для ввода текста шрифте, который по необходимости можно изменить на любой другой.



Читайте также: Как форматировать текст в документе Word

Заключение

Из этой небольшой статьи вы узнали, как сделать дробь в текстовом редакторе Ворд любых версий. Как видите, данную задачу можно решить несколькими способами, а инструментарий программы еще и позволяет автоматизировать ее выполнение.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

8 ответов:

Читайте также

Решение уравнений часто предполагает переход от исходного уравнения к уравнению, для которого известен метод нахождения корней и по корням которого можно определить корни исходного уравнения. В этой статье мы рассмотрим все основные преобразования уравнений, позволяющие осуществлять такие переходы. Здесь мы остановимся, во-первых, на преобразованиях, приводящих к уравнениям, имеющим те же корни, что и исходное уравнение. Во-вторых, поговорим о преобразованиях, приводящих к уравнениям, которые вместе со всеми корнями исходного уравнения могут иметь и другие корни. В-третьих, рассмотрим преобразования, которые сопряжены с вероятностью потери корней. Здесь же, естественно, разберемся, как избежать потери корней при проведении преобразований. Наконец, поразмышляем, какие преобразования вообще не стоит использовать для решения уравнений. Как всегда, весь материал снабдим поясняющими примерами.

Что понимают под преобразованием уравнения?

В школьных учебниках [1, 2] нет конкретных формулировок по вопросам, что такое преобразование уравнения и что значит преобразовать уравнение. Но имеющейся там информации вполне достаточно для самостоятельного ответа на них. Постараемся это сделать в доступной форме.

Определение

Преобразовать уравнение — это значит выполнить некоторые действия с уравнением, его частями и/или входящими в его состав выражениями.

Приведем пример. Возьмем конкретное уравнение 6·x=15 и выполним с ним конкретное действие – разделим обе части этого уравнения на 3. В результате имеем (6·x):3=15:3. Так, выполнив деление обеих частей уравнения 6·x=15 на 3, мы преобразовали это уравнение, в результате проведенного преобразования мы получили новое уравнение (6·x):3=15:3.

Определение

Действия, которые проводят с уравнениями, называют преобразованиями уравнения.

В приведенном выше примере мы проводили такое преобразование уравнения, как деление обеих частей уравнения на 3.

Таким образом, преобразование уравнения – это с одной стороны процесс, заключающийся в выполнении какого-то действия с уравнением, а с другой стороны – само это действие.

Для чего нужны преобразования уравнений? С их помощью можно решать уравнения. Каким образом? Определенные преобразования, о которых речь пойдет в следующем пункте, позволяют переходить от уравнения к равносильному ему уравнению или уравнению-следствию. Умелое использование таких преобразований дает возможность выстроить цепочку равносильных уравнений и уравнений-следствий с довольно простым в плане решения конечным уравнением, что позволяет по корням последнего уравнения найти все корни исходного уравнения.

Давайте разберем все основные преобразования, которые используются при решении уравнений.

К началу страницы

Список основных преобразований, использующихся при решении уравнений

Наиболее часто при решении уравнений используются следующие преобразования:

• Замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями.
• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа.
• Прибавление к обеим частям уравнения одного и того же выражения или вычитание из обеих частей уравнения одного и того же выражения.
• Перенос слагаемого из одной части уравнения в другую со знаком, измененным на противоположный.
• Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля.
• Умножение или деление обеих частей уравнения на одно и то же выражение.

К началу страницы

Другие преобразования

В представленный в предыдущем пункте список мы намеренно не включили такие преобразования, как возведение обеих частей уравнения в одну и ту же натуральную степень, логарифмирование, потенцирование обеих частей уравнения, извлечение корня одной степени из обеих частей уравнения, освобождение от внешней функции и другие. Дело в том, что эти преобразования не столь общи: преобразования из приведенного выше списка используются при решении уравнений всех видов, а только что упомянутые преобразования — по большей части для решения определенных видов уравнений (иррациональных, показательных, логарифмических и т.д.). Они подробно рассмотрены в рамках соответствующих методов решения уравнений. Вот ссылки, по которым можно выйти на их детальное описание:

• Возведение обеих частей уравнения в одну и ту же натуральную степень.
• Логарифмирование обеих частей уравнения.
• Потенцирование обеих частей уравнения.
• Извлечение корня одной и той же степени из обеих частей уравнения.
• Освобождение от одинаковой внешней функции.
• Замена выражения, отвечающего одной из частей исходного уравнения, выражением из другой части исходного уравнения.

Приведенные ссылки содержат исчерпывающую информацию по перечисленным преобразованиям. Поэтому, на них в этой статье мы больше не будем останавливаться. Вся последующая информация относится к преобразованиям из списка основных преобразований.

К началу страницы

Что получается в результате преобразования уравнения?

Проведение всех перечисленных выше преобразований может дать или уравнение, имеющее те же корни, что и исходное уравнение, или уравнение, среди корней которого содержатся все корни исходного уравнения, но которое может иметь еще и другие корни, или уравнение, среди корней которого будут не все корни преобразованного уравнения. В следующих пунктах мы разберем, какие из этих преобразований при выполнении каких условий к каким уравнениям приводят. Это крайне важно знать для успешного решения уравнений.

К началу страницы

Равносильные преобразования уравнений

Особый интерес представляют преобразования уравнений, дающие в результате их проведения равносильные уравнения, то есть, уравнения, имеющие то же множество корней, что и исходное уравнение. Такие преобразования называют равносильными преобразованиями. В школьных учебниках соответствующее определение не приводится в явном виде, но оно легко читается из контекста:

Определение

Равносильные преобразования уравнений – это преобразования, дающие равносильные уравнения.

Так чем же интересны равносильные преобразования? Тем, что если с их помощью удастся прийти от решаемого уравнения к довольно простому равносильному уравнению, то решение этого уравнения даст искомое решение исходного уравнения.

Из перечисленных в предыдущем пункте преобразований не все являются всегда равносильными. Некоторые преобразования являются равносильными лишь при определенных условиях. Составим список утверждений, которые определяют, какие преобразования и при каких условиях являются равносильными преобразованиями уравнения. Для этого за основу возьмем приведенный выше список, и к преобразованиям, которые не всегда равносильны, добавим условия, придающие им равносильность. Вот этот список:

• Замена выражения в левой или правой части уравнения тождественно равным ему выражением, при которой не изменяется ОДЗ переменных для уравнения, является равносильным преобразованием уравнения.

Поясним, почему это так. Для этого возьмем уравнение с одной переменной (аналогичные рассуждения можно провести и для уравнений с несколькими переменными) вида A(x)=B(x), выражения в его левой и правой части мы обозначили как A(x) и B(x) соответственно. Пусть выражение C(x) тождественно равно выражению A(x), причем ОДЗ переменной x уравнения C(x)=B(x) совпадает с ОДЗ переменной x для исходного уравнения. Докажем, что преобразование уравнения A(x)=B(x) в уравнение C(x)=B(x) есть равносильное преобразование, то есть, докажем, что уравнения A(x)=B(x) и C(x)=B(x) равносильные.

Для этого достаточно показать, что любой корень исходного уравнения является корнем уравнения C(x)=B(x), а любой корень уравнения C(x)=B(x) является корнем исходного уравнения.

Начнем с первой части. Пусть q – корень уравнения A(x)=B(x), тогда при подстановке его вместо x мы получим верное числовое равенство A(q)=B(q). Так как выражения A(x) и C(x) тождественно равны и выражение C(q) имеет смысл (это следует из условия о том, что ОДЗ для уравнения C(x)=B(x) совпадает с ОДЗ для исходного уравнения), то справедливо числовое равенство A(q)=C(q). Дальше используем свойства числовых равенств. В силу свойства симметричности равенство A(q)=C(q) можно переписать как C(q)=A(q). Тогда в силу свойства транзитивности из равенств C(q)=A(q) и A(q)=B(q) следует равенство C(q)=B(q). Этим доказано, что q – корень уравнения C(x)=B(x).

Абсолютно аналогично доказывается и вторая часть, а вместе с этим и все утверждение в целом.

Суть разобранного равносильного преобразования состоит в следующем: оно позволяет отдельно работать с выражениями в левой и правой части уравнений, заменяя их тождественно равными выражениями на исходной ОДЗ переменных.

Самый банальный пример: мы можем заменить сумму чисел в правой части уравнения x=2+1 ее значением, при этом получится равносильное уравнение вида x=3. Действительно, мы заменили выражение 2+1 тождественно равным ему выражением 3, и при этом не изменилась ОДЗ уравнения. Еще пример: в левой части уравнения 3·(x+2)=7·x−2·x+4−1 мы можем раскрыть скобки, а в правой – привести подобные слагаемые, что приведет нас к равносильному уравнению 3·x+6=5·x+3. Полученное уравнение действительно является равносильным, так как мы заменяли выражения тождественно равными им выражениями и при этом получили уравнение, имеющее ОДЗ, совпадающее с ОДЗ для исходного уравнения.

• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа есть равносильное преобразование уравнения.

Докажем, что прибавление к обеим частям уравнения A(x)=B(x) одного и того же числа c дает равносильное уравнение A(x)+c=B(x)+c и что вычитание из обеих частей уравнения A(x)=B(x) одного и того же числа c дает равносильное уравнение A(x)−c=B(x)−c.

Пусть q – корень уравнения A(x)=B(x), тогда справедливо равенство A(q)=B(q). Свойства числовых равенств нам позволяют прибавлять к обеим частям верного числового равенства или вычитать из его частей одно и то же число. Обозначим это число как c, тогда справедливы равенства A(q)+c=B(q)+c и A(q)−c=B(q)−c. Из этих равенств следует, что q – корень уравнения A(x)+c=B(x)+c и уравнения A(x)−c=B(x)−c.

Теперь обратно. Пусть q – корень уравнения A(x)+c=B(x)+c и уравнения A(x)−c=B(x)−c, тогда A(q)+c=B(q)+c и A(q)−c=B(q)−c. Мы знаем, что вычитание одного и того же числа из обеих частей верного числового равенства дает верное числовое равенство. Также мы знаем, что прибавление к обеим частям верного числового равенства дает верное числовое равенство. Вычтем из обеих частей верного числового равенства A(q)+c=B(q)+c число с, а к обеим частям равенства A(x)−c=B(x)−c прибавим число c. Это нам даст верные числовые равенства A(q)+c−c=B(q)+c−c и A(q)−c+c=B(q)+c−c, откуда заключаем, что A(q)=B(q). Из последнего равенства следует, что q – корень уравнения A(x)=B(x).

Так доказано исходное утверждение в целом.

Приведем пример такого преобразования уравнений. Возьмем уравнение x−3=1, и преобразуем его, прибавив к его обеим частям число 3, после этого мы получим уравнение x−3+3=1+3, которое равносильно исходному. Понятно, что в полученном уравнении можно выполнить действия с числами, о чем мы говорили в предыдущем пункте списка, в результате имеем уравнение x=4. Так, выполняя равносильные преобразования, мы невзначай решили уравнение x−3=1, его корень – это число 4. Рассмотренное равносильное преобразование очень часто используется для избавления от одинаковых числовых слагаемых, находящихся в разных частях уравнения. Например, и в левой и в правой частях уравнения x²+1=x+1 присутствует одинаковое слагаемое 1, вычитание из обеих частей уравнения числа 1 позволяет перейти к равносильному уравнению x²+1−1=x+1−1 и дальше к равносильному уравнению x²=x, и тем самым избавиться от этих одинаковых слагаемых.

• Прибавление к обеим частям уравнения или вычитание из обеих частей уравнения выражения, ОДЗ для которого не уже, чем ОДЗ для исходного уравнения, является равносильным преобразованием.

Докажем это утверждение. То есть, докажем, что уравнения A(x)=B(x) и A(x)+C(x)=B(x)+C(x) равносильные при условии, что ОДЗ для выражения C(x) не уже, чем ОДЗ для уравнения A(x)=B(x).

Сначала докажем один вспомогательный момент. Докажем, что при указанных условиях ОДЗ уравнений до и после преобразования одинаковые. Действительно, ОДЗ для уравнения A(x)+C(x)=B(x)+C(x) можно рассматривать как пересечение ОДЗ для уравнения A(x)=B(x) и ОДЗ для выражения C(x). Из этого и из того, что ОДЗ для выражения С(x) по условию не уже, чем ОДЗ для уравнения A(x)=B(x), следует, что ОДЗ для уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) одинаковые.

Теперь докажем равносильность уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) при условии, что области допустимых значений для этих уравнений одинаковые. Доказательство равносильности уравнений A(x)=B(x) и A(x)−C(x)=B(x)−C(x) при указанном условии приводить не будем, так как оно аналогично.

Пусть q – корень уравнения A(x)=B(x), тогда справедливо числовое равенство A(q)=B(q). Так как ОДЗ уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) одинаковые, то выражение C(x) имеет смысл при x=q, значит, C(q) – это некоторое число. Если прибавить C(q) к обеим частям верного числового равенства A(q)=B(q), то это даст верное числовое неравенство A(q)+C(q)=B(q)+C(q), из которого следует, что q – корень уравнения A(x)+C(x)=B(x)+C(x).

Обратно. Пусть q – корень уравнения A(x)+C(x)=B(x)+C(x), тогда A(q)+C(q)=B(q)+C(q) – верное числовое равенство. Мы знаем, что вычитание одного и того же числа из обеих частей верного числового равенства дает верное числовое равенство. Вычтем C(q) из обеих частей равенства A(q)+C(q)=B(q)+C(q), это дает A(q)+C(q)−C(q)=B(q)+C(q)−C(q) и дальше A(q)=B(q). Следовательно, q – корень уравнения A(x)=B(x).

Так рассматриваемое утверждение полностью доказано.

Приведем пример проведения этого преобразования. Возьмем уравнение 2·x+1=5·x+2. Мы можем прибавить к его обеим частям, например, выражение −x−1. Прибавление этого выражения не изменит ОДЗ, значит, такое преобразование является равносильным. В результате его проведения получим равносильное уравнение 2·x+1+(−x−1)=5·x+2+(−x−1). Это уравнение можно преобразовать дальше: раскрыть скобки и выполнить приведение подобных слагаемых в его левой и правой части (см. первый пункт списка). После выполнения этих действий мы получим равносильное уравнение x=4·x+1. Часто рассматриваемое преобразование уравнений применяется для избавления от одинаковых слагаемых, находящихся одновременно в левой и правой части уравнения.

• Если в уравнении перенести слагаемое из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.

Это утверждение является следствием предыдущих.

Покажем, как проводится это равносильное преобразование уравнения. Возьмем уравнение 3·x−1=2·x+3. Перенесем слагаемое, например, 2·x из правой части в левую, изменив его знак. При этом получим равносильное уравнение 3·x−1−2·x=3. Еще можно перенести минус единицу из левой части уравнения в правую, изменив знак на плюс: 3·x−2·x=3+1. Наконец, приведение подобных слагаемых приводит нас к равносильному уравнению x=4.

• Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число является равносильным преобразованием.

Приведем доказательство.

Пусть A(x)=B(x) – некоторое уравнение и c – некоторое число, отличное от нуля. Докажем, что умножение или деление обеих частей уравнения A(x)=B(x) на число c является равносильным преобразованием уравнения. Для этого докажем, что уравнения A(x)=B(x) и A(x)·c=B(x)·c, а также уравнения A(x)=B(x) и A(x):c=B(x):c — равносильные. Это можно сделать так: доказать, что любой корень уравнения A(x)=B(x) является корнем уравнения A(x)·c=B(x)·c и корнем уравнения A(x):c=B(x):c, после чего доказать, что любой корень уравнения A(x)·c=B(x)·c, как и любой корень уравнения A(x):c=B(x):c является корнем уравнения A(x)=B(x). Сделаем это.

Пусть q – корень уравнения A(x)=B(x). Тогда справедливо числовое равенство A(q)=B(q). Изучив свойства числовых равенств, мы узнали, что умножение или деление обеих частей верного числового равенства на одно и то же число, отличное от нуля, приводит к верному числовому равенству. Умножив обе части равенства A(q)=B(q) на c, получим верное числовое равенство A(q)·c=B(q)·c, из которого следует, что q – корень уравнения A(x)·c=B(x)·c. А разделив обе части равенства A(q)=B(q) на c, получим верное числовое равенство A(q):c=B(q):c, из которого следует, что q – корень уравнения A(x):c=B(x):c.

Теперь в другую сторону. Пусть q – корень уравнения A(x)·c=B(x)·c. Тогда A(q)·c=B(q)·c – верное числовое равенство. Разделив его обе части на отличное от нуля число c, получим верное числовое равенство A(q)·c:c=B(q)·c:c и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x). Если q – корень уравнения A(x):c=B(x):c. Тогда A(q):c=B(q):c – верное числовое равенство. Умножив его обе части на отличное от нуля число c, получим верное числовое равенство A(q):c·c=B(q):c·c и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x).

Утверждение доказано.

Приведем пример проведения этого преобразования. С его помощью можно, например, избавиться от дробей в уравнении . Для этого можно умножить обе части уравнения на 12. В результате получится равносильное уравнение вида , которое дальше можно преобразовать в равносильное уравнение 7·x−3=10, не содержащее в своей записи дробей.

• Умножение или деление обеих частей уравнения на одно и то же выражение, ОДЗ для которого не уже, чем ОДЗ для исходного уравнения и не обращающееся в нуль на ОДЗ для исходного уравнения, является равносильным преобразованием.

Докажем это утверждение. Для этого докажем, что если ОДЗ для выражения C(x) не уже, чем ОДЗ для уравнения A(x)=B(x), и C(x) не обращается в нуль на ОДЗ для уравнения A(x)=B(x), то уравнения A(x)=B(x) и A(x)·C(x)=B(x)·C(x), как и уравнения A(x)=B(x) и A(x):C(x)=B(x):C(x) — равносильные.

Пусть q – корень уравнения A(x)=B(x). Тогда A(q)=B(q) – верное числовое равенство. Из того, что ОДЗ для выражения C(x) не уже ОДЗ для уравнения A(x)=B(x) следует, что выражение C(x) имеет смысл при x=q. Значит, C(q) – это некоторое число. Причем C(q) отлично от нуля, что следует из условия не обращения выражения C(x) в нуль. Если умножить обе части равенства A(q)=B(q) на отличное от нуля число C(q), то это даст верное числовое равенство A(q)·C(q)=B(q)·C(q), из которого следует, что q – корень уравнения A(x)·C(x)=B(x)·C(x). Если разделить обе части равенства A(q)=B(q) на отличное от нуля число C(q), то это даст верное числовое равенство A(q):C(q)=B(q):C(q), из которого следует, что q – корень уравнения A(x):C(x)=B(x):C(x).

Обратно. Пусть q — корень уравнения A(x)·C(x)=B(x)·C(x). Тогда A(q)·C(q)=B(q)·C(q) – верное числовое равенство. Заметим, что ОДЗ для уравнения A(x)·C(x)=B(x)·C(x) такая же, как ОДЗ для уравнения A(x)=B(x) (это мы обосновали в одном из предыдущих пунктов текущего списка). Так как C(x) по условию не обращается на ОДЗ для уравнения A(x)=B(x) в нуль, то C(q) – отличное от нуля число. Разделив обе части равенства A(q)·C(q)=B(q)·C(q) на отличное от нуля число C(q), получим верное числовое равенство A(q)·C(q):C(q)=B(q)·C(q):C(q) и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x). Если q — корень уравнения A(x):C(x)=B(x):C(x). Тогда A(q):C(q)=B(q):C(q) – верное числовое равенство. Умножив обе части равенства A(q):C(q)=B(q):C(q) на отличное от нуля число C(q), получим верное числовое равенство A(q):C(q)·C(q)=B(q):C(q)·C(q) и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x).

Утверждение доказано.

Для наглядности приведем пример проведения разобранного преобразования. Осуществим деление обеих частей уравнения x³·(x²+1)=8·(x²+1) на выражение x²+1. Это преобразование равносильное, так как выражение x²+1 не обращается в нуль на ОДЗ для исходного уравнения и ОДЗ этого выражения не уже, чем ОДЗ для исходного уравнения. В результате проведения этого преобразования получим равносильное уравнение x³·(x²+1):(x²+1)=8·(x²+1):(x²+1), которое можно дальше преобразовать к равносильному уравнению x³=8.

К началу страницы

Преобразования, приводящие к уравнениям-следствиям

В предыдущем пункте мы разобрали, какие преобразования из списка основных преобразований и при каких условиях являются равносильными. Теперь посмотрим, какие из этих преобразований и при каких условиях приводят к уравнениям-следствиям, то есть, к уравнениям, которые содержат все корни преобразовываемого уравнения, но помимо них могут иметь и другие корни – посторонние корни для исходного уравнения.

Преобразования, приводящие к уравнениям-следствиям, востребованы не меньше равносильных преобразований. Если с их помощью удастся получить довольно простое в плане решения уравнение, то его решение и последующее отсеивание посторонних корней даст решение исходного уравнения.

Заметим, что все равносильные преобразования можно считать частными случаями преобразований, которые приводят к уравнениям-следствиям. Оно и понятно, ведь равносильное уравнение есть частный случай уравнения-следствия. Но с практической точки зрения более полезным является знание о том, что рассматриваемое преобразование именно равносильное, а не приводящее к уравнению-следствию. Разъясним, почему это так. Если мы знаем, что преобразование является равносильным, то полученное в результате его проведения уравнение точно не будет иметь корней, посторонних для исходного уравнения. А преобразование, приводящее к уравнению-следствию, может быть причиной появления посторонних корней, что обязывает нас в дальнейшем проводить дополнительное действие – отсеивание посторонних корней. Поэтому, в этом пункте статьи мы основное внимание сосредоточим на преобразованиях, в результате проведения которых могут появиться посторонние корни для исходного уравнения. И действительно важно уметь отличать такие преобразования от равносильных преобразований, чтобы четко понимать, когда необходимо проводить отсеивание посторонних корней, а когда это делать не обязательно.

Проанализируем весь список основных преобразований уравнений, приведенный во втором пункте данной статьи, с целью поиска преобразований, в результате проведения которых могут появиться посторонние корни.

• Замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями.

Мы доказали, что это преобразование является равносильным, если при его проведении не изменяется ОДЗ. А если ОДЗ изменится, что при этом произойдет? Сужение ОДЗ может повлечь потерю корней, подробнее об этом речь пойдет в следующем пункте. А при расширении ОДЗ могут появиться посторонние корни. Обосновать это не сложно. Приведем соответствующие рассуждения.

Пусть выражение C(x) такое, что оно тождественно равно выражению A(x) и ОДЗ для уравнения C(x)=B(x) шире, чем ОДЗ для уравнения A(x)=B(x). Докажем, что уравнение C(x)=B(x) – это следствие уравнения A(x)=B(x), и что среди корней уравнения C(x)=B(x) могут быть корни, посторонние для уравнения A(x)=B(x).

Пусть q – корень уравнения A(x)=B(x). Тогда A(q)=B(q) – верное числовое равенство. Так как ОДЗ для уравнения C(x)=B(x) шире, чем ОДЗ для уравнения A(x)=B(x), то выражение C(x) определено при x=q. Тогда, учитывая тождественное равенство выражений C(x) и A(x), заключаем, что C(q)=A(q). Из равенств C(q)=A(q) и A(q)=B(q) в силу свойства транзитивности вытекает равенство C(q)=B(q). Из этого равенства следует, что q – это корень уравнения C(x)=B(x). Это доказывает, что при указанных условиях уравнение C(x)=B(x) является следствием уравнения A(x)=B(x).

Остается обосновать, что уравнение C(x)=B(x) может иметь корни, отличные от корней уравнения A(x)=B(x). Докажем, что любой корень уравнения C(x)=B(x) из ОДЗ для уравнения A(x)=B(x) является корнем уравнения A(x)=B(x). Путь p – корень уравнения C(x)=B(x), принадлежащий ОДЗ для уравнения A(x)=B(x). Тогда C(p)=B(p) – верное числовое равенство. Так как p принадлежит ОДЗ для уравнения A(x)=B(x), то выражение A(x) определено при x=p. Из этого и из тождественного равенства выражений A(x) и C(x) следует, что A(p)=C(p). Из равенств A(p)=C(p) и C(p)=B(p) в силу свойства транзитивности следует, что A(p)=B(p), значит, p – это корень уравнения A(x)=B(x). Этим доказано, что любой корень уравнения C(x)=B(x) из ОДЗ для уравнения A(x)=B(x) является корнем уравнения A(x)=B(x). Другими словами, на ОДЗ для уравнения A(x)=B(x) не может быть корней уравнения C(x)=B(x), которые являются посторонними корнями для уравнения A(x)=B(x). Но по условию ОДЗ для уравнения C(x)=B(x) шире, чем ОДЗ для уравнения A(x)=B(x). А это допускает существование числа r, принадлежащего ОДЗ для уравнения C(x)=B(x) и не принадлежащего ОДЗ для уравнения A(x)=B(x), являющегося корнем уравнения C(x)=B(x). То есть, уравнение C(x)=B(x) может иметь корни, посторонние для уравнения A(x)=B(x), причем все они будут принадлежать тому множеству, на которое расширяется ОДЗ для уравнения A(x)=B(x) при замене в нем выражения A(x) тождественно равным ему выражением C(x).

Итак, замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями, в результате которой расширяется ОДЗ, в общем случае приводит к уравнению-следствию (то есть, может привести к возникновению посторонних корней) и лишь в частном случае приводит к равносильному уравнению (в том случае, если полученное уравнение не будет иметь корней, посторонних для исходного уравнения).

Приведем пример проведения разобранного преобразования. Замена выражения в левой части уравнения тождественно равным ему выражением x·(x−1) приводит к уравнению x·(x−1)=0, при этом происходит расширение ОДЗ – в нее добавляется число 0. Полученное уравнение имеет два корня 0 и 1, причем подстановка этих корней в исходное уравнение показывает, что 0 – это посторонний корень для исходного уравнения, а 1 – корень исходного уравнения. Действительно, подстановка нуля в исходное уравнение дает не имеющее смысла выражение , так как в нем присутствует деление на нуль, а подстановка единицы дает верное числовое равенство , что то же самое 0=0.

Обратите внимание, что подобное преобразование похожего уравнения в уравнение (x−1)·(x−2)=0, в результате проведения которого тоже расширяется ОДЗ, не приводит к появлению посторонних корней. Действительно, оба корня полученного уравнения (x−1)·(x−2)=0 — числа 1 и 2, являются корнями исходного уравнения, в чем легко убедиться путем проверки подстановкой. Этими примерами мы еще раз хотели подчеркнуть, что замена выражения в левой или правой части уравнения тождественно равным ему выражением, при которой расширяется ОДЗ, не обязательно приводит к появлению посторонних корней. Но может и приводить к их появлению. Так что, если в процессе решения уравнения такое преобразование имело место быть, то обязательно нужно проводить проверку с целью выявления и отсеивания посторонних корней.

Наиболее часто ОДЗ уравнения может расшириться и могут появиться посторонние корни из-за замены нулем разности одинаковых выражений или суммы выражений с противоположными знаками, из-за замены нулем произведений с одним или несколькими нулевыми множителями, из-за сокращения дробей и из-за использования свойств корней, степеней, логарифмов и т.д.

• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа.

Выше мы показали, что это преобразование всегда равносильное, то есть, приводящее к равносильному уравнению. Идем дальше.

• Прибавление к обеим частям уравнения одного и того же выражения или вычитание из обеих частей уравнения одного и того же выражения.

В предыдущем пункте мы добавили условие про то, что ОДЗ для прибавляемого или вычитаемого выражения должна быть не уже, чем ОДЗ для преобразовываемого уравнения. Это условие сделало рассматриваемое преобразование равносильным. Здесь имеют место рассуждения, аналогичные рассуждениям, приведенным в начале этого пункта статьи касательно того, что равносильное уравнение – это частный случай уравнения-следствия и что знание о равносильности преобразования практически полезнее знания об этом же преобразовании, но с позиций того, что оно приводит к уравнению-следствию.

А может ли в результате прибавления одного и того же выражения или вычитания одного и того же выражения из обеих частей уравнения получиться уравнение, которое помимо всех корней исходного уравнения будет иметь какие-либо еще корни? Нет, не может. Если ОДЗ для прибавляемого или вычитаемого выражения не уже, чем ОДЗ для исходного уравнения, то в результате прибавления или вычитания получится равносильное уравнение. Если же ОДЗ для прибавляемого или вычитаемого выражения будет уже, чем ОДЗ для исходного уравнения, то это может привести к потере корней, а не к появлению посторонних корней. Подробнее об этом поговорим в следующем пункте.

• Перенос слагаемого из одной части уравнения в другую со знаком, измененным на противоположный.

Это преобразование уравнения всегда равносильное. Поэтому нет смысла рассматривать его как преобразование, приводящее к уравнению-следствию, по озвученным выше причинам.

• Умножение или деление обеих частей уравнения на одно и то же число.

В предыдущем пункте мы доказали, что если умножение или деление обеих частей уравнения проводится на отличное от нуля число, то это является равносильным преобразованием уравнения. Поэтому, опять же, нет говорить о нем, как о преобразовании, приводящем к уравнению-следствию.

Но здесь стоит обратить внимание на оговорку про отличие от нуля числа, на которое проводится умножение или деление обеих частей уравнения. Для деления эта оговорка понятна – с начальных классов мы уяснили, что на нуль делить нельзя. А зачем эта оговорка для умножения? Давайте поразмыслим, к чему приведет умножение обеих частей уравнения на нуль. Для наглядности возьмем конкретное уравнение, например, 2·x+1=x+5. Это линейное уравнение, имеющее единственный корень, которым является число 4. Запишем уравнение, которое получится при умножении обеих частей этого уравнения на нуль: (2·x+1)·0=(x+5)·0. Очевидно, корнем этого уравнения является любое число, ведь при подстановке в это уравнение вместо переменной x любого числа получается верное числовое равенство 0=0. То есть, в нашем примере умножение обеих частей уравнения на нуль привело к уравнению-следствию, что явилось причиной появления бесконечного множества посторонних корней для исходного уравнения. Причем, стоит заметить, что в этом случае обычные способы отсеивания посторонних корней не справляются со своей задачей. Значит, проделанное преобразование бесполезно для решения исходного уравнения. И это типичная ситуация для рассматриваемого преобразования. Именно поэтому такое преобразование, как умножение обеих частей уравнения на нуль, не используется для решения уравнений. Это преобразование и другие преобразования, которые не следует использовать для решения уравнений, нам еще предстоит разобрать в последнем пункте.

• Умножение или деление обеих частей уравнения на одно и то же выражение.

В предыдущем пункте мы доказали, что это преобразование является равносильным при выполнении двух условий. Напомним их. Первое условие: ОДЗ для этого выражения должна быть не уже, чем ОДЗ для исходного уравнения. Второе условие: выражение, на которое проводится умножение или деление, не должно обращаться в нуль на ОДЗ для исходного уравнения.

Давайте изменим первое условие, то есть, будем считать, что ОДЗ для выражения, на которое планируется умножение или деление обеих частей уравнения, уже, чем ОДЗ для исходного уравнения. В результате проведения такого преобразования будет получено уравнение, ОДЗ для которого будет уже, чем ОДЗ для исходного уравнения. Такие преобразования могут привести к потере корней, о них мы будем говорить в следующем пункте.

А что будет, если убрать второе условие про не обращение в нуль значений выражения, на которое проводится умножение или деление обеих частей уравнения, на ОДЗ для исходного уравнения?

Деление обеих частей уравнения на одно и то же выражение, которое обращается в нуль на ОДЗ для исходного уравнения, приведет к уравнению, ОДЗ которого будет уже, чем ОДЗ для исходного уравнения. Действительно, ведь из нее выпадут числа, обращающие в нуль выражение, на которое было проведено деление. Это может привести к потере корней.

А как обстоят дела с умножением обеих частей уравнения на одно и то же выражение, которое обращается в нуль на ОДЗ для исходного уравнения? Можно показать, что при умножении обеих частей уравнения A(x)=B(x) на выражение C(x), ОДЗ для которого не уже, чем ОДЗ для исходного уравнения, и которое обращается в нуль на ОДЗ для исходного уравнения, получается уравнение-следствие, которое помимо всех корней уравнения A(x)=B(x) может иметь и другие корни. Сделаем это, тем более что этот пункт статьи как раз посвящен преобразованиям, приводящим к уравнениям-следствиям.

Пусть выражение C(x) такое, что ОДЗ для него не уже, чем ОДЗ для уравнения A(x)=B(x), и оно обращается в нуль на ОДЗ для уравнения A(x)=B(x). Докажем, что при этом уравнение A(x)·C(x)=B(x)·C(x) есть следствие уравнения A(x)=B(x).

Пусть q – корень уравнения A(x)=B(x). Тогда A(q)=B(q) – верное числовое равенство. Так как ОДЗ для выражения C(x) не уже, чем ОДЗ для уравнения A(x)=B(x), то выражение C(x) определено при x=q, значит, C(q) – это некоторое число. Умножение обеих частей верного числового равенства на любое число дает верное числовое равенство, поэтому, A(q)·C(q)=B(q)·C(q) — верное числовое равенство. Значит q – корень уравнения A(x)·C(x)=B(x)·C(x). Этим доказано, что любой корень уравнения A(x)=B(x) является корнем уравнения A(x)·C(x)=B(x)·C(x), откуда следует, что уравнение A(x)·C(x)=B(x)·C(x) есть следствие уравнения A(x)=B(x).

Заметим, что при указанных условиях уравнение A(x)·C(x)=B(x)·C(x) может иметь корни, посторонние для исходного уравнения A(x)=B(x). Ими являются все такие числа из ОДЗ для исходного уравнения, которые обращают выражение C(x) в нуль (все числа, обращающие в нуль выражение C(x) являются корнями уравнения A(x)·C(x)=B(x)·C(x), так как их подстановка в указанное уравнение дает верное числовое равенство 0=0), но которые не являются корнями уравнения A(x)=B(x). Уравнения A(x)=B(x) и A(x)·C(x)=B(x)·C(x) при указанных условиях будут равносильными тогда, когда все числа из ОДЗ для уравнения A(x)=B(x), обращающие в нуль выражение C(x), являются корнями уравнения A(x)=B(x).

Итак, умножение обеих частей уравнения на одно и то же выражение, ОДЗ для которого не уже, чем ОДЗ для исходного уравнения, и которое обращается в нуль на ОДЗ для исходного уравнения, в общем случае приводит к уравнению-следствию, то есть, может привести к появлению посторонних корней.

Приведем пример для иллюстрации. Возьмем уравнение x+3=4. Его единственным корнем служит число 1. Умножим обе части этого уравнения на одно и то же выражение, обращающееся в нуль на ОДЗ для исходного уравнения, например, на x·(x−1). Это выражение обращается в нуль при x=0 и x=1. Умножение обеих частей уравнения на это выражение даст нам уравнение (x+3)·x·(x−1)=4·x·(x−1). Полученное уравнение имеет два корня: 1 и 0. Число 0 – это посторонний корень для исходного уравнения, появившийся в результате проведенного преобразования.

К началу страницы

Преобразования, проведение которых может привести к потере корней

Некоторые преобразования из списка основных преобразований при определенных условиях могут привести к потере корней. Например, при делении обеих частей уравнения x·(x−2)=x−2 на одно и то же выражение x−2 происходит потеря корня. Действительно, в результате проведения такого преобразования получается уравнение x=1 с единственным корнем, которым является число 1, а исходное уравнение имеет два корня 1 и 2.

Нужно отчетливо понимать, когда происходит потеря корней в результате проведения преобразований, чтобы при решении уравнений не терять корни. Давайте разбираться с этим.

В результате проведения указанных преобразований потеря корней может произойти тогда и только тогда, когда ОДЗ для преобразованного уравнения оказывается уже, чем ОДЗ для исходного уравнения.

Для доказательства этого утверждения нужно обосновать два момента. Во-первых, нужно доказать, что если в результате проведения указанных преобразований уравнения сужается ОДЗ, то может произойти потеря корней. И, во-вторых, нужно обосновать, что если в результате проведения указанных преобразований происходит потеря корней, то ОДЗ для полученного уравнения уже, чем ОДЗ для исходного уравнения.

Если ОДЗ для уравнения, полученного в результате преобразования, уже, чем ОДЗ для исходного уравнения, то, естественно, ни один корень исходного уравнения, находящийся вне ОДЗ для полученного уравнения, не может быть корнем уравнения, полученного в результате проведения преобразования. Значит, все эти корни будут потеряны при переходе от исходного уравнения к уравнению, ОДЗ для которого уже, чем ОДЗ для исходного уравнения.

Теперь обратно. Докажем, что если в результате проведения указанных преобразований происходит потеря корней, то ОДЗ для полученного уравнения уже, чем ОДЗ для исходного уравнения. Это можно сделать методом от противного. Предположение о том, что в результате проведения указанных преобразований происходит потеря корней, но не сужается ОДЗ, противоречит утверждениям, доказанным в предыдущих пунктах. Действительно, из этих утверждений следует, что если при проведении указанных преобразований не сужается ОДЗ, то получаются или равносильные уравнения или уравнения-следствия, значит, не может происходить потеря корней.

Итак, причиной возможной потери корней при проведении основных преобразований уравнений выступает сужение ОДЗ. Понятно, что, решая уравнения, мы не должны терять корни. Здесь, естественно, возникает вопрос: «Что же делать, чтобы не терять корни при преобразовании уравнений»? Ответим на него в следующем пункте. А сейчас давайте пробежимся по списку основных преобразований уравнений, чтобы более детально посмотреть, какие преобразования могут привести к потере корней.

• Замена выражений, находящихся в левой и правой частях уравнения, тождественно равными им выражениями.

Если заменить выражение в левой или правой части уравнения тождественно равным выражением, ОДЗ для которого уже, чем ОДЗ для исходного уравнения, то это приведет к сужению ОДЗ, и из-за этого могут быть потеряны корни. Наиболее часто к сужению ОДЗ и, как следствие, к возможной потере корней приводят замены выражений в левой или правой части уравнений тождественно равными им выражениями, проводящиеся на базе некоторых свойств корней, степеней, логарифмов и некоторых тригонометрических формул. Например, замена выражения в левой части уравнения тождественно равным ей выражением , сужает ОДЗ и приводит к потере корня −16. Аналогично, замена выражения в левой части уравнения тождественно равным ему выражением приводит к уравнению , ОДЗ для которого уже, чем ОДЗ для исходного уравнения, что влечет потерю корня −3.

• Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа.

Это преобразование равносильное, поэтому, при его проведении не могут быть потеряны корни.

• Прибавление к обеим частям уравнения одного и того же выражения или вычитание из обеих частей уравнения одного и того же выражения.

Если прибавить или вычесть выражение, ОДЗ которого уже, чем ОДЗ для исходного уравнения, то это приведет к сужению ОДЗ и, как следствие, к возможной потере корней. Это стоит иметь в виду. Но здесь стоит отметить, что на практике обычно приходится прибегать к прибавлению или вычитанию выражений, которые присутствуют в записи исходного уравнения, что не приводит к изменению ОДЗ и не влечет потери корней.

• Перенос слагаемого из одной части уравнения в другую со знаком, измененным на противоположный.

Это преобразование уравнения равносильное, поэтому, в результате его проведения корни не теряются.

• Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля.

Это преобразование тоже равносильное, и из-за него потеря корней не происходит.

• Умножение или деление обеих частей уравнения на одно и то же выражение.

Это преобразование может приводить к сужению ОДЗ в двух случаях: когда ОДЗ для выражения, на которое проводится умножение или деление, уже, чем ОДЗ для исходного уравнения, и когда проводится деление на выражение, обращающееся в нуль на ОДЗ для исходного уравнения. Заметим, что на практике обычно не приходится прибегать к умножению и делению обеих частей уравнения на выражение с более узкой ОДЗ. А вот с делением на выражение, обращающееся на ОДЗ для исходного уравнения в нуль, иметь дело приходиться. Существует метод, позволяющий справляться с потерей корней при таком делении, о нем мы расскажем в следующем пункте этой статьи.

К началу страницы

Как избежать потери корней?

Если для преобразования уравнений использовать только преобразования из списка основных преобразований и при этом не допускать сужения ОДЗ, то потери корней не произойдет.

Означает ли это, что нельзя проводить какие-либо другие преобразования уравнений? Нет, не означает. Если придумать какое-нибудь еще преобразование уравнения и полностью описать его, то есть, указать, когда оно приводит к равносильным уравнениям, когда – к уравнениям-следствиям, и когда может приводить к потере корней, то его вполне можно будет взять на вооружение.

Стоит ли полностью отказываться от преобразований, сужающих ОДЗ? Не стоит этого делать. В своем арсенале не помешает оставить преобразования, при которых из ОДЗ для исходного уравнения выпадает конечное количество чисел. Почему от таких преобразований не стоит отказываться? Потому что существует метод, позволяющий в таких случаях избежать потери корней. Он состоит в отдельной проверке чисел, выпадающих из ОДЗ, на предмет того, есть ли среди них корни исходного уравнения. Проверить это можно подстановкой этих чисел в исходное уравнение. Те из них, которые при подстановке дают верное числовое равенство, являются корнями исходного уравнения. Их нужно включить в ответ. После такой проверки можно спокойно проводить задуманное преобразование без боязни потерять корни.

Типичным преобразованием, при котором ОДЗ для уравнения сужается на несколько чисел, является деление обеих частей уравнения на одно и то же выражение, которое обращается в нуль в нескольких точках из ОДЗ для исходного уравнения. Такое преобразование лежит в основе метода решения возвратных уравнений. Но оно используется и при решении уравнений других видов. Приведем пример.

Решение уравнения можно провести методом введения новой переменной. Чтобы ввести новую переменную, надо разделить обе части уравнения на 1+x. Но при таком делении может произойти потеря корня, так как хотя ОДЗ для выражения 1+x не уже, чем ОДЗ для исходного уравнения, но выражение 1+x обращается в нуль при x=−1, а это число принадлежит ОДЗ для исходного уравнения. Значит, может произойти потеря корня −1. Чтобы исключить потери корня, следует отдельно проверить, является ли −1 корнем исходного уравнения. Для этого можно подставить −1 в исходное уравнение и посмотреть, какое равенство при этом получается. В нашем случае подстановка дает равенство , что то же самое 4=0. Это равенство неверное, значит −1 не является корнем исходного уравнения. После такой проверки можно осуществлять задуманное деление обеих частей уравнения на 1+x, не опасаясь за то, что может произойти потеря корней.

В заключение этого пункта еще раз обратимся к уравнениям из предыдущего пункта и . Преобразование этих уравнений на базе тождеств и приводит к сужение ОДЗ, а это влечет потерю корней. В этом пункте мы сказали, что для того, чтобы не терять корни, нужно отказаться от преобразований, сужающих ОДЗ. Значит, от указанных преобразований нужно отказаться. А как же быть? Можно провести преобразования не на базе тождеств и , из-за которых сужается ОДЗ, а на базе тождеств и . В результате перехода от исходных уравнений и к уравнениям и не происходит сужения ОДЗ, значит, не будут потеряны корни.

Здесь же особо отметим, что при замене выражений тождественно равными выражениями нужно тщательно следить за тем, чтобы выражения были именно тождественно равными. Например, в уравнении нельзя заменить выражение x+3 выражением с целью упрощения вида левой части до , так как выражения x+3 и не являются тождественно равными, ведь их значения не совпадают при x+3<0. В нашем примере такое преобразование приводит к потере корня. А в общем случае замена выражения не тождественно равным выражением приводит к уравнению, которое не позволяет получить решение исходного уравнения.

К началу страницы

Преобразования уравнений, к которым не следует прибегать

Преобразований, которые упоминаются в этой статье, обычно достаточно для нужд практики. То есть, не стоит сильно озадачиваться придумыванием каких-либо еще преобразований, лучше сосредоточиться на правильном использовании уже проверенных.

Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.

Приведём примеры для понимания самого смысла логарифма:

Основное логарифмическое тождество:

Свойства логарифмов, которые необходимо всегда помнить:

*Логарифм произведения равен сумме логарифмов сомножителей.

* * *

*Логарифм частного (дроби) равен разности логарифмов сомножителей.

* * *

*Логарифм степени равен произведению показателя степени на логарифм ее основания.

* * *

*Переход к новому основанию

* * *

Ещё свойства:

* * *

Вычисление логарифмов тесно связано с использованием свойств показателей степени.

Перечислим некоторые из них:

Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:

Следствие из данного свойства:

* * *

При возведении степени в степень основание остаётся прежним, а показатели перемножаются.

* * *

Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.

Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!

На этом всё! Успеха Вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Что такое логарифм? Как решать логарифмы?

Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:

1. Поймете, что такое логарифм
.

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…

Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

Замечание по поводу логарифмический уравнений

Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения
, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.

В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:

log 2 x
= 4

А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.

Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений
. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.

И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!

Решение логарифмического уравнения в задаче C1

Итак, решаем уравнение:

В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:

Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c
одержали, обязательно нужно привести к уравнению вида:

log a
f
(x
) = log a
g
(x
)

Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:

1. Слева у нас стоит сумма двух чисел
   , одно из которых вообще не является логарифмом.
2. Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.

Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения
, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.

Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.

Сумма логарифмов и логарифм произведения

Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:

log a
f
(x
) + log a
g
(x
) = log a
f
(x
) · g
(x
)

Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:

a
= log b
b
a

Здесь нужно понимать: когда мы говорим «Любое основание b
», то подразумеваем, что b
все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения
, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:

Давайте посмотрим, что происходит в нашем случае:

1 = log 2 2 1 = log 2 2

Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:

Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания
. Переходим к следующему шагу.

Правила вынесения степеней из логарифма

Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:

log a
b
n
= n
· log a
b

Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n
«мигрировало» из логарифма наружу и стало коэффициентом спереди.

С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:

Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k
.

Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:

Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.

И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.

Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:

Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:

Наконец, перепишем исходное уравнение с учетом новых коэффициентов:

log 2 2(9x
2 + 5) = log 2 (8x
4 + 14)

Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.

Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.

Деление дроби на дробь: дополнительные соображения

Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:

Давайте разберемся, что такое дробь. Запишем:

А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:

Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.

Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.

Избавление от знака логарифма

Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:

2(9x
2 + 5) = 8x
4 + 14

Давайте раскроем скобки слева. Получим:

18x
2 + 10 = 8x
4 + 14

Перенесем все из левой части в правую:

8x
4 + 14 − 18x
2 − 10 = 0

Приведем подобные и получим:

8x
4 − 18x
2 + 4 = 0

Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:

4x
4 − 9x
2 + 2 = 0

Перед нами обычное биквадратное уравнение
, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:

D
= 81 − 4 · 4 · 2 = 81 − 32 = 49

Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x
, а x
2 , потому что у нас биквадратное уравнение. Итак, наши варианты:

Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная
. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.

Теперь расписываем второй корень нашего биквадратного уравнения:

Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:

Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!

Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x
2 + 5 (эта функция всегда положительна), либо 8x
4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.

Прекрасно, теперь переходим ко второй части задачи.

Отбор корней логарифмического уравнения на отрезке

Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:

Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.

Иррациональные корни

Начнем с иррациональных корней. Заметим, что 8/9

Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.

Рациональные корни

Остается два корня: x
= 1/2 и x
= −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x
= −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x
= 1/2. Этот корень также лежит на рассматриваемом отрезке.

Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:

Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.

Давайте отметим подходящие корни на оси координат:

Окончательным ответом будут два корня: 1/2 и −1/2.

Сравнение иррациональный чисел: универсальный алгоритм

В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V
— знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:

Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:

Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.

Как это делается? Делаем то же самое, что и с обычными неравенствами:

1. Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак
   . Вот такая галочка V изменилась бы на такую — Λ.
2. Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат
   , чтобы избавится от радикала.

Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.

При решении это оформляется вот таким образом:

Теперь это все легко сравнивается. Дело в том, что 64/81

Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.

Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому
логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a
или b
, именно логарифм, равный другому логарифму.

Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.

Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:

1. Привести все свободные элементы к логарифму;
2. Затем эти логарифмы сложить;
3. В полученной конструкции все логарифмы привести к одному и тому же основанию.

В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

дробный калькулятор с корнями

Вы искали дробный калькулятор с корнями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор дробей с корнями, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «дробный калькулятор с корнями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как дробный калькулятор с корнями,калькулятор дробей с корнями,калькулятор дробей со степенями и корнями,калькулятор дробей со степенями онлайн с решением,калькулятор квадратов чисел,калькулятор корень уравнения,калькулятор онлайн корней уравнений,калькулятор онлайн с дробями и корнями онлайн калькулятор,калькулятор онлайн с дробями и с корнями калькулятор,калькулятор онлайн с корнями и дробями онлайн калькулятор,калькулятор радикалов,калькулятор с дробями и корнями и степенями,калькулятор с корнями дробный,калькулятор с корнями и дробями,калькулятор с корнями и дробями и степенями,калькулятор с корнями и дробями онлайн,калькулятор с корнями и степенями и дробями,калькулятор с корнями с решением,калькулятор с кубами и квадратами,калькулятор сокращения дробей с буквами и степенями онлайн,калькулятор степеней с дробями онлайн,калькулятор уравнений с корнями,найти значение выражения с дробями и степенями онлайн,онлайн калькулятор квадратов,онлайн калькулятор корней с решением,онлайн калькулятор корней уравнений,онлайн решение выражений с корнями,онлайн решение примеров с корнями,онлайн решить пример с корнями,решение выражений с корнями онлайн,решение примеров онлайн с корнями,решение примеров с корнями онлайн,решение примеров с корнями онлайн калькулятор с решением,решить выражение онлайн с корнями,решить выражение с корнями онлайн,решить онлайн пример с корнями,решить пример онлайн с корнями,сложение корней калькулятор,сократить дробь с корнями онлайн калькулятор. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и дробный калькулятор с корнями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор дробей со степенями и корнями).

Где можно решить любую задачу по математике, а так же дробный калькулятор с корнями Онлайн?

Решить задачу дробный калькулятор с корнями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Калькулятор онлайн для расчетов процентов, дробей, степеней

Калькулятор давно и прочно вошел в нашу жизнь. Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.

Функции онлайн-калькулятора

Функции онлайн-калькулятора

Клавиша	Символ	Операция
pi	pi	Постоянная pi
е	е	Число Эйлера
%	%	Процент
( )	( )	Открыть/Закрыть скобки
,	,	Запятая
sin	sin (α)	Синус угла
cos	cos (β)	Косинус
tan	tan (y)	Тангенс
sinh	sinh ()	Гиперболический синус
cosh	cosh ()	Гиперболический косинус
tanh	tanh ()	Гиперболический тангенс
sin-1	asin ()	Обратный синус
cos-1	acos ()	Обратный косинус
tan-1	atan ()	Обратный тангенс
sinh-1	asinh ()	Обратный гиперболический синус
cosh-1	acosh ()	Обратный гиперболический косинус
tanh-1	atanh ()	Обратный гиперболический тангенс
x2	^2	Возведение в квадрат
х3	^3	Возведение в куб
xy	^	Возведение в степень
10x	10^()	Возведение в степень по основанию 10
ex	exp ()	Возведение в степень числа Эйлера
vx	sqrt (x)	Квадратный корень
3vx	sqrt3 (x)	Корень 3-ей степени
yvx	sqrt (x,y)	Извлечение корня
log2x	log2 (x)	Двоичный логарифм
log	log (x)	Десятичный логарифм
ln	ln (x)	Натуральный логарифм
logyx	log (x,y)	Логарифм
I / II		Сворачивание/Вызов дополнительных функций
Unit		Конвертер величин
Matrix		Матрицы
Solve		Уравнения и системы уравнений
		Построение графиков
Дополнительные функции (вызов клавишей II)
mod	mod	Деление с остатком
!	!	Факториал
i / j	i / j	Мнимая единица
Re	Re ()	Выделение целой действительной части
Im	Im ()	Исключение действительной части
|x|	abs ()	Модуль числа
Arg	arg ()	Аргумент функции
nCr	ncr ()	Биноминальный коэффициент
gcd	gcd ()	НОД
lcm	lcm ()	НОК
sum	sum ()	Суммарное значение всех решений
fac	factorize ()	Разложение на простые множители
diff	diff ()	Дифференцирование
Deg		Градусы
Rad		Радианы

Виды калькуляторов

В зависимости от возможностей и сферы применения калькуляторы бывают простые, бухгалтерские, финансовые, инженерные.

• Бухгалтерскими калькуляторами пользуются бухгалтера и кассиры для арифметических расчетов с денежными суммами.
• Для финансовых расчетов пользуются финансовыми калькуляторами, у которых к стандартному набору математических функций добавлены операции со сложными процентами и функции, характерные для банковской сферы и финансовых приложений.
• Специализированные — это калькуляторы, применяемые для вычислений в конкретной сфере деятельности (строительные, ипотечные, статистические, медицинские).
• Печатающие — калькуляторы, которые с помощью печатающего устройства выводят полученные результаты, расчеты, графики и вычисления на бумажную ленту.

Отдельно выделяются:

• программируемые калькуляторы, используемые для выполнения сложных вычислений по заранее заложенной программе пользователя;
• графические, выполняющие построение и отображение графиков функций.

Простейший калькулятор предназначен выполнять ординарные арифметические расчеты (сложение, вычитание и т.п.), вычислять процент, извлекать квадратный корень, возводить число в степень. Помимо простых расчетов, строителям и архитекторам, инженерно-техническим и научным работникам, математикам и геодезистам, старшеклассникам и студентам технических специальностей очень часто приходится решать важнейшие инженерные задачи, осуществлять сложные математические расчеты.

Представленный на сайте тригонометрический калькулятор выполняет расчет:

• синусов;
• косинусов;
• тангенсов;
• котангенсов.

А также обратных тригонометрических функций:

• арксинусов;
• арккосинусов;
• арктангенсов;
• арккотангенсов.

Все тригонометрические расчеты с углами выполняются в радианах, градах и градусах.

На нашем сайте вы сможете пользоваться инженерным онлайн калькулятором, предназначенным для инженерных и научных расчетов разного уровня сложности.

Инженерный калькулятор позволяет:

• производить сложные расчеты с дробями;
• возводить любое число в степень, извлекать корень из числа;
• рассчитать онлайн проценты, логарифмы, интегралы любой сложности;
• выполнять необходимые математические операции с одной или несколькими матрицами;
• находить производную онлайн как от элементарной, так и от сложной функции;
• решать алгебраические, линейные, логарифмические, тригонометрические и другие уравнения.

Онлайн калькулятор прост и понятен в обращении, применять его не составит труда тем, кто пользуется настольным инженерным калькулятором, принципы работы функций и программ аналогичны. По своему виду инженерный калькулятор онлайн имитирует настоящий калькулятор, поэтому для ознакомления с ним вам не понадобится много времени.

решение уравнений онлайн со степенями

Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.

Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.

С его помощью вы сможете вводить данные, при этом используя интерфейсные визуальные кнопки либо непосредственно клавиатуру. Кроме этого предоставленный калькулятор онлайн позволить осуществить расчеты сложных выражений, к примеру:(21-45)/(1.52)(8+2*2)=-96.

Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы. В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.

2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:

1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).

2. Если , то (правило извлечения корня из дроби).

3. Если , то (правило извлечения корня из корня).

4. Если , то (правило возведения корня в степень).

5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.

6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.

7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:

(правило умножения корней),

(правило деления корней),

8. Правило вынесения множителя из-под знака корня. При .

9. Обратная задача — внесение множителя под знак корня. Например,

10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.

При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним. Выполнить действия со степенями самостоятельно, а затем посмотреть решения.

Калькулятор предназначен для решения показательных уравнений онлайн.
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.

Калькулятор предназначен для решения показательных уравнений онлайн.
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.

Для того чтобы найти решение показательного уравнения, необходимо ввести это уравнение в ячейку. В ответе получаем корни уравнения, а также график показательной функции.
Калькулятор решает любые показательные уравнения онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step и Approximate form.

Решения показательных уравнений. Показательная функция всегда монотонна и она принимает только положительные значения.

https://okcalc.com/ru/equation/

https://www.function-x.ru/powers_and_radicals.html

https://allcalc.ru/node/667

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Определение 1

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.

Чуть сложнее работать со степенью, имеющей рациональный  и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.

В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Пример 1

Вычислите значение степенного выражения 23·(42−12).

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.

Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.

Ответ: 23·(42−12)=32.

Пример 2

Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Пример 3

Представьте выражение со степенями 9-b3·π-12 в виде произведения.

Решение

Представим число 9 как степень 32 и применим формулу сокращенного умножения:

9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1

Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений. 

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

Определение 2

• ar·as=ar+s;
• ar:as=ar−s;
• (a·b)r=ar·br;
• (a:b)r=ar:br;
• (ar)s=ar·s.

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Пример 4

Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.

Ответ: a2,5·(a2)−3:a−5,5=a2.

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Пример 5

Найти значение степенного выражения 313·713·2123.

Решение

Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.

Есть еще один способ провести преобразования:

313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21

Ответ: 313·713·2123=31·71=21

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание
 
Пример 6

Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.

Решение

Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.

Ответ: t3−t−6.

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Пример 7

Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2

Ответ:  3·523·513-5-231+2·x2-3-3·x2=-122+x2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример 8

Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a0,3:

a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a

б) Обратим внимание на знаменатель:

x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162

Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
 

Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12

Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.  

Пример 9

Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.

Получаем:

30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14

Ответ:  а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Пример 10

Выполните действия x12+1×12-1-x12-1×12+1·1×12.

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x12-1·x12+1

Вычтем числители:

x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12

Теперь умножаем дроби:

4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12

Произведем сокращение на степень x12, получим 4×12-1·x12+1.

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.

Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1

Пример 11

Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение

Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.

Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями:  x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.

Переходим от последнего произведения к дроби x138x2,7+1.

Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить  на x3·(x+1)0,2.

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x19·x·x36 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами  x≥0  и x·x3≥0 ,  которые задают множество [0, +∞).

На этом множестве мы имеем право перейти от корней к степеням: 

x19·x·x36=x19·x·x1316

Используя свойства степеней, упростим полученное степенное выражение.

x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13

Ответ: x19·x·x36=x13.

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.

Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения:

5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0

Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.

Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Комплексные корни и степени чисел онлайн

Вы ввели следующее выражение

Результат вычисления степени

Результат выражения (альтернативный вывод) со всеми корнями

Этот онлайн калькулятор  рассчитывает любые степени действительных или комплексных чисел.

Поможет Вам рассчитать корень комплексного числа, возвести в степень действительное или комплексное выражение.

Рассчитывает степень любого числа

Хотелось бы заметить, что возведение любого действительного числа в дробную степень, не так сложно как может показаться на первый взгляд.

то есть, если мы хотим возвести число 3 в степень 

то  решение такое

Итого

Если речь идет о комплексных числах,  то  возведение степень и извлечени корня осуществляется по уравнению Муавра.

Формулы следующие:

Для возведения в степень

— модуль комплексного числа

— аргумент комплексного числа

Для извлечения корня

где p = 0, 1, …, k—1.

Есть еще третий возможный вариант, когда  не только основание является комплексным числом, но и степень этого числа также число комплексное.

Конечно возникает желание использовать формулу Муавра и преобразовать её, для наших нужд, но мы воспользуемся первым вариантом вычисления степеней.

то есть вот этой формулой 

Формула  расчета логарифа комплексного числа известна

здесь k — может принимать любые целые  значения, поэтому говорят, что логарифм комплексного числа многозначен.

Для практических целей используется главное значение(k=0)

Формула расчета экспоненты комплексного числа тоже

Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного  числа.

Синтаксис 

Если используете XMPP клиент:  step_i <запрос>

Если используете этот сайт:  <запрос>

где запрос  — состоит  из двух чисел. Сначала идет основание потом  в другом окне степень.

Основание может быть как действительным числом так и комплексным, положительным или отрицательным

Комплексное значение пишется как x:y  где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i

Степень может  быть быть целым числом,как положительным так и отрицательным.

Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. В таком случае альтернативный вывод покажет Вам, все 2 или все 7 корней соответственно.

Степень может быть комплексным числом записанным как в нормальной форме через символ i, так  и через сокращенную запись x:y, где x- действительная часть числа, y — мнимая часть числа

Замечание: В поле можно вводить только числа и никак не выражение, если у Вас есть желание посчитать вот такое выражение 

то эта страница вам не поможет, Вам надо  использовать универсальный калькулятор комплексных чисел

где x- это основание, а y-степень

Примеры

Например: взять степень 2/5 от комплексного числа 1-2.5i

Пишем 1:-2.5 2/5 или если делаете запрос через Jabber  step_i 1:-2.5 2/5

Ответ получим

Комплексное число 1:-2.5 в степени 2/5 равно

Действительная часть: 1.3209 Комплексная часть: -0.6812
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667

---

Интересно, а чему будет равна мнимая единица в степени мнимой единицы?

пишем i i

и получаем что 

---

возведем еще одно число в комплексную степень.

число 1+i в комплексную степень 1-i

результат вот такой 

• Конвертер и калькулятор в разные системы счисления онлайн >>

Решить уравнение со степенями онлайн калькулятор. Решение показательных уравнений по математике

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте.{nm}:]

Прибавляем к исходному уравнению:

Вынесем за скобки

Выразим

Поскольку степени одинаковые, отбрасываем их:

Ответ:

Где можно решить показательное уравнение онлайн решателем?

Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.

для решения математики. Быстро найти решение математического уравнения
в режиме онлайн
. Сайт www.сайт позволяет решить уравнение
почти любого заданного алгебраического
, тригонометрического
или трансцендентного уравнения онлайн
. При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн
. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн
займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн
— это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн
, тригонометрические уравнения онлайн
, трансцендентные уравнения онлайн
, а также уравнения
с неизвестными параметрами в режиме онлайн
. Уравнения
служат мощным математическим аппаратом решения
практических задач. C помощью математических уравнений
можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений
можно найти, сформулировав задачу на математическом
языке в виде уравнений
и решить
полученную задачу в режиме онлайн
на сайте www.сайт. Любое алгебраическое уравнение
, тригонометрическое уравнение
или уравнения
содержащие трансцендентные
функции Вы легко решите
онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений
. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн
. Поэтому для решения математических уравнений онлайн
мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн
, тригонометрических уравнений онлайн
, а также трансцендентных уравнений онлайн
или уравнений
с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений
ресурса www.. Решая уравнения онлайн
самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений
на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение
, после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн
и сравнить ответы. Это поможет Вам избежать ошибок в решении
и вовремя скорректировать ответ при решении уравнений онлайн
будь то алгебраическое
, тригонометрическое
, трансцендентное
или уравнение
с неизвестными параметрами.

Назначение сервиса
. Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).

Инструкция
. Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.

где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат .
Рекомендуется также ознакомиться с основными действиями над матрицами .

Пример №1
. Задание
. Найти решение матричного уравнения
Решение
. Обозначим:

Тогда матричное уравнение запишется в виде: A·X·B = C.

Определитель матрицы А равен detA=-1

Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1

Пример №2
. Задание.
Решить матричное уравнение
Решение
. Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.

Определитель матрицы А равен detA=0

Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.

Пример №3
. Задание. Найти решение матричного уравнения

Решение
. Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.

Определитель матрицы А равен detA=-60

Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1

Найдем обратную матрицу A -1 .

Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1

Ответ: >

Удобный и простой онлайн калькулятор дробей с подробным решением
может:

• Складывать, вычитать, умножать и делить дроби онлайн,
• Получать готовое решение дробей картинкой и удобно его переносить.



Результат решения дробей будет тут…

0
1
2
3
4
5
6
7
8
9

Знак дроби «/»
+
—
*
:

_cтереть
Очистить

У нашего онлайн калькулятора дробей быстрый ввод
. Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7
в калькулятор и нажмите кнопку «Решать дроби
«.
Калькулятор напишет вам подробное решение дробей
и выдаст удобную для копирования картинку
.

Знаки используемые для записи в калькуляторе

Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.

Возможности онлайн калькулятора дробей

Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.

Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.

Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.

Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.

Дискриминант

Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D
   = 0, есть ровно один корень;
3. Если D
   > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x
   2 − 8x
   + 12 = 0;
2. 5x
   2 + 3x
   + 7 = 0;
3. x
   2 − 6x
   + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x
   2 − 2x
   − 3 = 0;
2. 15 − 2x
   − x
   2 = 0;
3. x
   2 + 12x
   + 36 = 0.

Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.

D
> 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.

D
> 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left(-1 right)}=-5; & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left(-1 right)}=3. end{align}]

Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x
   2 + 9x
   = 0;
2. x
   2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0.

Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax
   2 + c
   = 0 выполнено неравенство (−c
   /a
   ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c
   /a
   )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x
   2 − 7x
   = 0;
2. 5x
   2 + 30 = 0;
3. 4x
   2 − 9 = 0.

x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.

5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.

Калькулятор Корней — Найдите квадратный корень

калькулятор корней онлайн корня поможет вам найти квадратный корень n-й степени любого положительного числа, которое вы хотите. Кроме того, этот калькулятор sqrt сообщает вам, что введенное вами число является точным квадратом или не является идеальным квадратом. Например; 4, 9 и 16 – это идеальные квадраты 2, 3 и 4 соответственно. Квадратный корень из числа – это число, которое при умножении на себя равно исходному числу. Например, квадрат 9 и 16 равен 3 и 4 соответственно. Если вы беспокоитесь о простом ручном вычислении, продолжайте читать, чтобы узнать формулу квадратного корня, вычисление дроби, отрицательные числа и многое другое!

Кроме того, вы можете попробовать наш онлайн калькулятор корней, который поможет вам вычислить значение любого числа, возведенного в любую степень.

Но давайте перейдем к основам!

Проведите по!

Как найти квадратный корень (шаг за шагом):

Чтобы подготовиться к вычислению квадратного корня, вам следует запомнить основной идеальный квадратный корень. Поскольку квадрат 1, 4, 9, 16, 25, 100 равен 1, 2, 3, 4, 5 и 10.

Чтобы найти квадрат √25, давайте посмотрим!

√25 = √5 * 5

√25 = √52

√25 = 5

Это простейшие квадратные корни, потому что они всегда дают целое число, но что, если у числа нет точного квадратного корня? Например, вы должны оценить квадрат в 54?

• Как вы знаете, √49 = 7 & √64 = 8. Итак, √54 находится между 8 и 7.
• Число 54 ближе к 49, чем к 64. Итак, вы можете попробовать угадать √54 = 7,45.
• Затем возводя в квадрат 7,45, получаем 7,452 = 55,5, что больше 54. Поэтому вам следует попробовать меньшее число. Возьмем 7,3
• Если взять в квадрат 7,3, получим 53,29, что близко к 54.
• Это означает, что квадратный корень из 54 находится между 7,3 и 7,4. 1/2 = √a / √b = √a / b

  Где a / b – любая дробь. Приведем еще один пример:

  Пример:

  Что такое квадратный корень из 9/25?

  Решение:

  √9 / 25 = √9 / √25

  √9 / √25 = 3/5 = 0,6

  Квадратный корень отрицательного числа:

  В школе нас учили, что квадратный корень из отрицательных чисел не может существовать. Но математики вводят общий набор чисел (Комплексные числа). В виде,

  х = а + би

  Где a – действительное число, а b – мнимая часть. Йота (i) – это комплексное число со значением:

  я = √-1. Приведем несколько примеров:

  Квадрат -4 = √-4 = √-1 * 9 = √ (-1) √9 = 3i

  Чему равен квадратный корень из -17 = √-17 = √-1 * 17 = √ (-1) √17 = 17i

  Как пользоваться калькулятором квадратного корня:

  С помощью этого калькулятор корней онлайн квадратный корень стало очень просто. Для точных расчетов вам просто нужно выполнить указанные шаги.

  Читать дальше!

  Входы:

  • Прежде всего, нажмите вкладку, чтобы выбрать квадратный корень или корень n-й степени для любого числа.
  • Затем введите число, для которого вы хотите произвести расчет в соответствии с выбранной опцией.
  • Наконец, нажмите кнопку «Рассчитать».

  Выходы:

  Как только вы закончите, калькулятор покажет:

  • Корень квадратный из числа.
  • Корень N-й степени числа.
  • Пошаговый расчет.

  Заметка:

  Независимо от того, какой параметр ввода, онлайн-калькулятор с корнями корня покажет вам точные результаты в соответствии с выбранным вводом.

  Часто задаваемые вопросы (FAQ):
  Может ли число иметь более одного квадратного корня?

  Да, положительные числа имеют более одного sqrt, одно положительное, а другое отрицательное.

  Является ли √2 рациональным числом?

  Нет, это иррациональное число.

  Причина:

  Квадратный корень из 2 не может быть выражен как частное двух чисел.

  Рациональны ли квадратные корни?

  Некоторые корни рациональны, а другие иррациональны.

  Конечное примечание:

  Квадратные корни часто встречаются в математических формулах, включая квадратную формулу, дискриминант, а также во многих законах физики. Кроме того, он используется во многих местах повседневной жизни, используется инженерами, плотниками, менеджерами по строительству, фельдшерами и многими другими. Когда дело доходит до вычислений для большого количества, это очень сложно и сложно. Просто попробуйте калькулятор корней онлайн, который поможет вам определить квадратный корень в соответствии с вашими потребностями.

  Other languages: Square Root Calculator, Karekök Hesaplama, Kalkulator Akar Kuadrat, Kalkulator Pierwiastków, Wurzel Ziehen Rechner, 平方根 計算, 제곱근 계산, Kalkulačka Odmocniny, Calculadora De Raiz Quadrada, Calculatrice Racine Carré, Calculadora Raiz Cuadrada, Calcolo Radice Quadrata, حاسبة الجذر التربيعي, Neliöjuuri Laskin, Kvadratrot Kalkulator, Kvadratni Koren Kalkulator.

  Онлайн-калькулятор предалгебры

  Наших пользователей:

  Я чувствую себя прекрасно, что больше не нужно выполнять домашние задания, задания и тесты. Я закончила школу. Наконец-то получил свой B.S. в телекоммуникациях. Ура! Спасибо за помощь и новую версию. Желаю тебе всего наилучшего.
  S.D., Орегон

  Я хочу поблагодарить вас за вашу помощь. Ваша помощь в решении того, как решить проблему, помогла мне понять, как решать проблемы, и на самом деле получить правильный результат.Спасибо.
  до н.э., Флорида

  Это хорошая новость для любой школы, учителя или студента, когда такая фантастическая программа разработана специально для алгебры. Отличная работа!
  Джеймс Мур, Мичиган

  ---

  Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?

  Поисковые фразы, использованные в 25.02.2012:

  • Уравнение радиуса для предварительной алгебры
  • дроби стихотворения по математике
  • LCD рабочие листы
  • год Семь по математике {углы}
  • умножение для начинающих
  • ti 83 plus, найти ковариацию
  • полууглов
  • Определение «квадратного корня» четвертой степени
  • сложнейшие задачи факторинга
  • процентов формулы
  • алгебра 2 glencoe Mathematics ответы
  • преобразовать десятичное число в соотношение
  • гипербола x3 + y3 целочисленных кубов
  • Алгебра-умножение и деление выражений

  Руководство по решениям

  • для математического опыта houghton mifflin
  • Распечатки по математике для шестого класса бесплатно
  • Упростить экспоненциальные выражения TI-84
  • Алгебра 2-факторный калькулятор специальных продуктов
  • калькулятор корней второго порядка
  • преобразование смешанных дробей в десятичные
  • статистика элементарных экзаменационных вопросов
  • План урока с доказательством квадратичной формулы
  • рабочие листы с пропорциями
  • как решить линейные дифференциалы
  • методы преобразования десятичной дроби в дробную
  • буквальные уравнения для чайников
  • метод замены на манекены
  • формулы TI84
  • Упростите калькулятор алгебраических дробей
  • колледж + математика 100 бесплатных упражнений
  • Корень квадратный из 7 в 9-й степени
  • Решение задачи по дробям при делении
  • программа для решения научных уравнений
  • даже математика ответы эллипсы mathbook
  • программа по алгебре для 9 класса
  • ГЕОМЕТРИЧЕСКИЕ РЕШЕНИЯ ДЛЯ ПРЕСС-ЗАЛА
  • процентных уравнений
  • harcourt math georgia edition / практическое домашнее задание
  • Дроби по математике ответы на вопросы
  • Как решить пифагорейские тождества
  • Калькулятор полиномиальных выражений делительной степени

  Код ответа на вопросы по книге прентис-холла

  • Математические коды
  • Калькулятор ТИ-83, корней
  • Решатель полиномов факторинга
  • решение алгебраических уравнений игры
  • Справка по элементарной алгебре
  • ключ ответа для алгебры гленко 1
  • свертка для ti 89
  • онлайн-решатель уравнений линейный
  • Прентис Холл Алгебра 2 онлайн-учебник
  • год 9 вопросов по математике продвинутого уровня
  • вычислить 2 в 4-й степени
  • расчет РАДИКАЛЬНЫЙ
  • графические уравнения Прентиса Холла 89
  • Рабочий лист «Test Of Genius»
  • aptitude решен вопрос
  • Программа факторинга ТИ-84
  • объединяет две 3D-анимации в клене
  • Системные уравнения 9-го класса
  • степень решателя задач
  • сложнейший математический вопрос
  • многослойные листы третьего сорта
  • онлайн-калькулятор экспонентов
  • решение нескольких уравнений одновременно
  • «Рабочий лист расширения»
  • Самый простой способ найти LCM
  • бесплатный калькулятор для решения уравнений с квадратными корнями
  • Калькулятор квадратного уравнения и факторинга
  • как делать множители по математике для детей
  • художественная алгебра
  • Макдугал Литтел Помощь в домашнем задании по структуре и методам алгебры

  Рабочий лист

  • логарифмов
  • бесплатных заданий по математике для девятого класса
  • овладение физикой ключ ответа
  • решить уравнение 3-го порядка
  • Масштабные коэффициенты онлайн по математике
  • Glencoe рабочая тетрадь по алгебре дополнение учителей
  • Алгебра 2 ПО
  • парабол; упрощенный коэффициент разницы
  • предалгебра с pizzazz
  • кубических сурда год 10
  • Калькулятор экспонент и радикалов
  • перевода рабочих листов по математике
  • прентис холл алгебра 1 (издание 2004 г.) учитель том

  Калькулятор дробных показателей | Как упростить рациональные экспоненты?

  При работе с дробными показателями есть несколько условий.Вы можете увидеть их все и узнать, как решать дробные показатели с разными условиями. Они следующие

  • Дробные экспоненты с числителем 1
  • Дробные экспоненты с числителем, отличным от 1 (любые дроби)

  Дробные экспоненты с числителем 1

  Дробные экспоненты — это способ выражения степеней вместе с корнями в одной нотации. Давайте посмотрим на несколько примеров, числитель которых равен 1, и узнаем, как они называются.

  36 ^1/2 = √36

  27 ³ = 27

  Первый показатель степени 1/2 называется квадратным корнем, а следующий показатель степени 1/3 называется кубическим корнем. Если мы продолжим так же. Показатель 1 / k называется k-м корнем.

  x ^{1 / k} = ^k √x

  Дробные экспоненты с числителем, отличным от 1 (любые дроби)

  В случаях, когда числитель не равен 1 (n 1)

  a = x ^{н / д}

  Вам просто нужно возвести число в степень n и вынуть из него корень d.Вам не нужно беспокоиться о порядке, так как вы можете разделить его на две части.

  • Целое число (n)
  • Дробь Часть (1 / d)

  x ^{n / d} = x ( ^{n.1 / d} ) = (x ⁿ ) ^{1 / d} = (x ^{1 / d} ) ⁿ

  x ^{n / d} = d√x ⁿ = (d√x) ⁿ

  Вы можете выбрать любой из удобных для вас методов и провести вычисления.

  Пример: вычислить дробную экспоненту 16 ^3/2 ?

  Раствор:

  Дан дробный показатель степени 16 ^3/2

  16 ^3/2 = 16 ^{(3. 1/2)}

  = (16 ³ ) ^1/2

  = √16 ³

  = √4096

  = 64

  Сделайте все свои математические задачи проще и быстрее с нашим онлайн-калькулятором.Сайт гуру предоставил бесплатные онлайн-калькуляторы для различных математических и статистических концепций.

  Калькулятор дробной степени

  Этот калькулятор дробной степени поможет вам — сюрприз, сюрприз — дробные показатели. Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения.

  Дробные показатели с числителем 1

  Дробные показатели — это способ выражения степеней, а также корней в одном представлении .

  Что именно это означает? Давайте сначала рассмотрим несколько простых примеров, где наш числитель равен 1 :

  .

  • 64 ^(1/2) = √64
  • 27 ^(1/3) = ³√27

  Из приведенных выше уравнений мы можем вывести, что:

  • Показатель степени 1/2 — это квадратный корень
  • Показатель степени 1/3 — это кубический корень
  • Показатель степени 1/4 — корень четвертой степени
  • …
  • Показатель степени 1 / k является корнем k-й степени

  Но почему это так? Постараемся это доказать:

  1. Давайте воспользуемся законом экспонент, который гласит, что мы можем складывать показатели при умножении двух степеней с одинаковым основанием:

     x ^{a + b} = x ^a * x ^b

     так, например, если n = 2

     x² = x¹⁺¹ = x¹ * x¹ = x * x

     Попробуйте это с любым числом, которое вам нравится, это всегда правда!

  2. Затем давайте посмотрим на дробные показатели x:

     x = x¹ = x ^{(1/2 + 1/2)} = x ^(1/2) * x ^(1/2)

     Как позвонить по номеру, умножение которого само на себя дает другой номер? Конечно, это квадратный корень из ! Итак, мы выяснили, что:

     x ^(1/2) = √x

  3. Если хотите, вы можете аналогичным образом проверить другие корни, например.г. кубический корень:

     x = x ^{(1/3 + 1/3 + 1/3)} = x ^(1/3) * x ^(1/3) * x ^(1/3) = ³√x * ³√x * ³√x

     т.

     x ^(1/3) = ³√x

     Теперь мы знаем, что x в степени одной трети равен кубическому корню из x.

  Дробные показатели с числителем, отличным от 1 (любая дробь)

  Итак, что произойдет, если наш числитель не равен 1 (n 1)?

  Все, что вам нужно сделать, это возвести это число в степень n и взять корень d-th .Порядок не имеет значения, дробь n / d может быть разделена на две части:

  • целое число (n)
  • дробная часть (1 / d)

  Давайте посмотрим на пример, где дробная экспонента = 3/2 и x = 16:

  • 16 ^3/2 = 16 ^{(3 * 1/2)} = (16 ³ ) ^1/2 = √ (16³) = √4096 = 64

  Или, как вариант, можно написать, что

  • 16 ^3/2 = 16 ^{(1/2) * 3} = (16 ^1/2 ) ³ = (√16) ³ = 4³ = 64

  И результат действительно тот же.Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!

  Отрицательный и дробный показатель степени

  Положительные показатели говорят нам, сколько раз мы используем число при умножении:

  Но что произойдет, если наша экспонента будет отрицательным числом, вы можете догадаться? Да, он говорит вам, сколько раз вам нужно разделить на это число:

  Кроме того, вы можете просто вычислить положительную экспоненту (например, x ⁴ ), а затем взять обратную величину (в нашем случае 1 / x ⁴ ).Конечно, аналогично, если у нас есть отрицательная И дробная экспонента.

  Калькулятор степени дроби — как использовать

  Мы считаем, что этот инструмент настолько интуитивно понятен и прост, что никаких дополнительных пояснений не требуется, но для записи мы быстро объясним, как вычислить дробные показатели:

  1. Введите базовое значение . Например, введите 7.
  2. Введите числитель и знаменатель дроби .Если вы хотите использовать этот калькулятор как простой инструмент экспоненты — с целым числом в качестве показателя вместо дроби — введите 1 в качестве знаменателя. Предположим, наша дробь равна -2/5. Введите -2 в числитель и 5 в поле знаменателя (также отметьте обратную работу).
  3. Наслаждайтесь результатом, отображаемым нашим калькулятором дробной степени! Это 0,4592 для нашей примерной задачи.

  Надо ли говорить о гибкости нашего инструмента? Вам не нужно переходить калькулятор сверху вниз — вычислите любое неизвестное, какое захотите! Введите любые три значения, и четвертое появится в мгновение ока.

  Еще одна полезная функция калькулятора — дробью может быть не только показатель степени, но и основание ! Например, если вы хотите вычислить (1/16) ^1/2 , просто введите 1/16 в базовое поле. Отлично!

  Калькулятор дробей с показателями — Онлайн-калькулятор дробей с показателями

  ‘Cuemath’s Fractions with Exponents Calculator’ — это онлайн-инструмент, который помогает найти значение заданного показателя степени.

  Что такое калькулятор дробей с показателями?

  Онлайн-калькулятор дробей с показателями

  Cuemath поможет вам найти значение данного показателя дроби в течение нескольких секунд.

  Как использовать дроби с калькулятором показателей?

  Пожалуйста, выполните следующие шаги, чтобы найти значение заданной дробной экспоненты:

  • Шаг 1: Введите базовое число, числитель экспоненты и знаменатель в данное поле ввода.
  • Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти значение данной дробной экспоненты.
  • Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и найти значение другой дробной экспоненты.

  Как найти дроби с показателями?

  Показатель степени определяется как количество раз умножения основного числа на себя. Проще говоря, сколько раз конкретное число умножается само на себя, показано с помощью экспонент.

  Показатель степени выражается в форме: x ^{a / b} , где x — это базовое число, a / b представляет дробь, a — числитель, а b — знаменатель

  Хотите найти сложные математические решения за секунды?

  Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.

  Забронируйте бесплатную пробную версию Класс

  Решенный пример:

  Решить 4 ^-1/2 ?

  Решение:

  = 4 ^-1/2

  = 1/4 ^1/2

  = 1 / √4

  = 1/2

  Аналогично, вы можете попробовать калькулятор, чтобы найти дроби с показателями для

  1) 10 ^-3/2

  2) 9 ^3/2

  Калькулятор экспонент

  Попробуйте бесплатную программу для решения математических задач или прокрутите вниз до учебных пособий! Введите выражение, например.2-1 Пример задачи Ничья Количество решаемых уравнений: 23456789 Пример задачи Решить Введите неравенство в график, например.г. y Пример задачи Ничья 908 Количество решаемых неравенств: 23456789 Пример задачи Решить Наших пользователей: Я никогда ничего подобного не видел! Постепенно я изучаю сложную алгебру вместе со своими детьми! Лиза Шустер, Нью-Йорк Пока все отлично! М.Б., Иллинойс Переезжать из города в город сложно, особенно когда нужно понимать, как преподает каждый учитель. С Алгебратором кажется, что есть только один учитель, и тоже хороший. Теперь мне не нужно беспокоиться о том, чтобы справиться с алгеброй. Я ищу помощи и в других областях. Питер Гудман, TN Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою? Поисковые фразы, использованные в 2010-04-15: рабочий лист по математике для ks2 лаплас для чайников прентис холл математика алгебра один Общая викторина для второклассников Советы по алгебре для детей www.math trivia.com как вычесть десятичные дроби powerpoint Семь — это нечетное число, как вы можете сделать это даже без добавления, вычитания, умножения или деления добавление 5 или 6 к числовому листу Упрощение калькулятора абсолютных значений примеры перестановок начальная школа Пример программы операций с квадратной формулой с использованием базового программное обеспечение учебники по компасу для курсов повышения квалификации по математике площадь без математических расчетов сравнение рабочих листов для упорядочивания целых чисел простой способ вычисления дробей делительный и умножающий корень решение дробных показателей добавить отрицательные положительные целые числа для печати бесплатно Клен решить сложное уравнение решить нелинейное уравнение символьный matlab CLEP Calculus бесплатное онлайн-руководство Калькулятор сложения и вычитания радикальных выражений комбинаций упражнений по математике Заданий по алгебре для 6 класса алгебраические уравнения для дробей алгебраические уравнения экспоненциальные Решение квадратных уравнений с отрицательными показателями математические ответы читы загрузить visual ti 84 как взять 2 цифры после десятичной точки + java конвертировать y перехватить javascript Интересные мелочи по математике математическая культура один в майя Макдугал Литтел структура и метод алгебры и тригонометрии ответы Практика решения квадратных квадратичных листов Бухгалтерская книга + pdf саксонская алгебра 1 ответы парабола, изображения как решить дифференциальное уравнение с помощью Matlab поиск в Google / практический тест gre / перестановка бесплатные математические распечатки примеров математических мелочей с ответами за 4 класс как упростить показатели с помощью переменных Алгебра нахождение вершин по квадратичной формуле рабочие листы положительное отрицательное сложение вычитание слово проблема-образец и решения деление квадратного корня на дробь изучайте prealegbra онлайн бесплатно калькулятор трехчленов Алгебра , используемая в сети Калькулятор квадратного уравнения рудок «Глава 6», №7 онлайн-эмулятор калькулятора ти-84 бесплатных экзаменационных работ завершение вычисления квадрата Дискретная математика рабочий лист «уравнения баланса» математика вопросов для практики квадратичных функций 10 класс книга по математике формула 1 экзамен C3 график что такое разложение знаменателя на простые множители квадратных корня с использованием множителя Завершение квадратной конструкции Показатели по математике в шестом классе Калькулятор делителей общие ошибки при сложении и вычитании радикальных выражений помогают квадратные и квадратные корни, кубы и куберы графический калькулятор онлайн гипербола Калькулятор квадратного корня из дроби ks3 запись формулы рабочего листа texas ti-83 программное обеспечение для моделирования Упростить калькулятор квадратного корня решение уравнений 3-й степени преобразование десятичного числа в другое основание Учебник элементарной алгебры Рабочие листы по алгебре KS2 Порядок операций решения логарифмов изменение предмета n алгебраических формул бесплатные рабочие листы Калькулятор алгебры продвинутого уровня решить систему на TI 83 Как понимать алгебру Печатные листы с координатами для 5-го класса математика мелочи с ответами математика упростить вычисление корня как решить квадратные уравнения с использованием двух точек однородный дифференциал вопросов по начальной математике «Экзамены» Пирамиды сложения алгебры вычислить наибольший общий делитель TI-83 ROM скачать алгебра powerpoint по пропорциям контрольных по математике за год седьмой Упрощение алгебры калькулятор деление Образец онлайн-экзамена понятия дробей и квадратных корней решение однородных уравнений г. 8 учеников задачи по математике

  Как оценить корни с помощью научного калькулятора — видео и стенограмма урока

  Квадратный корень

  Чтобы вычислить квадратный корень, воспользуйтесь кнопкой квадратного корня на вашем научном калькуляторе.Чтобы использовать эту кнопку, вам необходимо знать, как работает ваш калькулятор. В некоторых калькуляторах сначала нужно ввести число, а затем нажать кнопку извлечения квадратного корня. В других случаях вы сначала нажимаете кнопку извлечения квадратного корня, а затем свое число. Так, например, чтобы найти квадратный корень из 5, вы нажмете эти кнопки, если в вашем калькуляторе вы сначала вводите число.

  Квадратный корень из 5 должен быть около 2,236.

  Пользовательская кнопка корня

  Чтобы найти другие корни, вы воспользуетесь специальной кнопкой, которая позволит вам выбрать корень.Если вы не видите такой кнопки, возможно, она находится в меню одной из функциональных клавиш.

  Вы можете использовать настраиваемую корневую кнопку , чтобы найти кубический, четвертый и пятый корни или любой положительный целочисленный корень. Чтобы использовать эту кнопку, вам нужно посмотреть руководство к вашему калькулятору. В некоторых калькуляторах вы сначала вводите число, затем кнопку корня, а затем желаемый корень. В других случаях вы выполняете эти операции в обратном порядке, начиная с желаемого корня, затем кнопки корня и числа.

  Чтобы найти кубический корень из 5 с помощью калькулятора, в который вы вводите желаемый корень последним, вы нажимаете следующие кнопки:

  Кубический корень из 5 должен быть около 1,7.

  Кнопка экспоненты

  Если в вашем калькуляторе нет настраиваемой кнопки корня, вы можете использовать кнопку настраиваемой степени, чтобы найти корень.

  Чтобы использовать кнопку настраиваемой экспоненты , преобразуйте желаемый корень в показатель степени, инвертируя его или используя 1 в качестве числителя и корня в качестве знаменателя дроби.Таким образом, кубический корень становится показателем 1/3, квадратный корень становится показателем или степенью 1/2, а корень пятой степени становится 1/5 и так далее.

  После преобразования желаемого корня используйте кнопки в круглых скобках, чтобы сообщить калькулятору, что у вас есть дробная экспонента. Итак, чтобы ввести квадратный корень из 9, нажмите эти кнопки:

  Помните, что в зависимости от вашего калькулятора вам может потребоваться сначала ввести дробную экспоненту, прежде чем нажимать кнопку настраиваемой экспоненты.символ). Если у вас есть, вы можете использовать его вместо кнопки настраиваемой экспоненты. Обе кнопки означают, что базовое число взято в степень.

  Практическая задача

  Давайте попробуем вычислить седьмой корень из 24. Если в вашем калькуляторе вы выбираете корень последним, вы нажимаете на кнопки, как это.

  Вы должны получить ответ около 1,5746.

  Резюме урока

  На этом уроке вы узнали, как использовать научный калькулятор для вычисления корней.Корень в математике относится к этому символу:

  Например, когда вы извлекаете квадратный корень из числа, вы ищете число, которое при умножении само на себя дает заданное число. Например, квадратный корень из 9 равен 3, потому что 3 умножения на себя равно 9.

  Кубический корень числа — это число, которое при трехкратном умножении на себя дает данное число. Кроме того, любое положительное целое число может иметь корень.

  При использовании научного калькулятора для нахождения корня вам необходимо следовать его руководству и посмотреть, вводите ли вы сначала число, а затем нажимаете кнопку корня, или наоборот. Пользовательская кнопка корня может использоваться для вычисления кубического, четвертого и пятого корней или любого положительного целочисленного корня.), которую можно использовать вместо кнопки настраиваемой экспоненты.

  Интернет-научный калькулятор — инструмент

  Скачать научный калькулятор eCalc

  Версия для Windows Версия для Mac OSX Просмотреть больше загрузок

  Онлайн-калькулятор и справка по математике

  Поддержка кнопок и клавиш

  Стек

  Поддон Intro

  Основные функции

  Дополнение

  Вычитание

  Умножение

  Дивизион

  Знак

  Площадь

  Квадратный корень

  Повышение мощности

  Естественная экспонента

  Логарифм

  Натуральный логарифм

  Обратный

  Показатель

  Факториал

  PI

  Тригонометрические функции онлайн

  Синус

  Обратный синус

  Косинус

  Обратный косинус

  Касательная

  Обратный тангенс

  Косеканс

  Обратный косеканс

  Секант

  Обратный секанс

  Котангенс

  Обратный котангенс

  Онлайн-гиперболические тригонометрические функции

  Гиперболический синус

  Гиперболический косинус

  Гиперболический тангенс

  Гиперболический косеканс

  Гиперболический секанс

  Гиперболический котангенс

  Обратный гиперболический синус

  Обратный гиперболический косинус

  Обратный гиперболический тангенс

  Обратный гиперболический косеканс

  Обратный гиперболический секанс

  Обратный гиперболический котангенс

  Меню

  Формат

  Уголок

  Система координат

  Режимы онлайн-калькулятора

  Система координат

  от десятичной дроби к дроби

  Комплексные числа

  Онлайн-конвертер единиц

  Библиотека констант

  Онлайн-решатель

  Базовый преобразователь

  Онлайн-калькулятор и справка по математике

  eCalc — это бесплатный и простой в использовании научный калькулятор, который поддерживает множество расширенных функций, включая преобразование единиц измерения, решение уравнений и даже математику с комплексными числами.eCalc предлагается как бесплатный онлайн-калькулятор, так и в виде калькулятора для загрузки.

  Режим ввода (алгебраический или RPN)

  Онлайн-калькулятор работает либо с алгебраическим вводом (режим по умолчанию), либо с вводом RPN. Режим калькулятора устанавливается щелчком по символу «ALG / RPN» в строке состояния или путем изменения режима в диалоговом окне меню.

  Алгебраический режим

  Алгебраический режим ввода обычно называют «инфиксной записью» и широко используется в большинстве портативных калькуляторов.Выражения, вводимые в режиме алгебраического ввода, выполняются способом, который очень похож на естественную форму выражения, а порядок операций определяется приоритетом операторов и скобками.

  Режим RPN

  RPN, что означает обратную польскую нотацию, представляет собой нотацию на основе стека, в которой операторы должны следовать за своими операндами. Например, чтобы оценить выражение «1 + 2» в RPN, пользователь должен ввести «1 2 +», и выражение вычисляется сразу после оператора.Выражения, содержащие круглые скобки, такие как «(1 + 2) * 3», оцениваются, отмечая порядок приоритета и вводя форму как «1 2 + 3 *».

  Поддержка графических кнопок и клавиатуры

  Онлайн-калькулятор поддерживает ввод данных с помощью графической кнопки или традиционных клавиш компьютерной клавиатуры. Пользователю предоставляется возможность использовать любой метод ввода, и оба они одинаково действительны; тем не менее, существуют некоторые тригонометрические функции (как указано ниже), которые ограничены вводом с клавиатуры компьютера, поскольку для размещения графических кнопок доступно ограниченное пространство.

  Стек

  Стек — это функция калькулятора, которая позволяет просматривать историю результатов. В стеке одновременно отображаются только 4 элемента, но можно прокручивать вверх и вниз по стеку, щелкая стрелки вверх и вниз над стопкой. Значения в стеке также можно «вытолкнуть» вниз в поле ввода калькулятора, щелкнув стрелки вниз слева от строки в стеке.

  Поддон Введение

  Калькулятор разделен на две части: интерфейс научного калькулятора слева и панель калькулятора справа.Поддон обеспечивает область отображения для специальных функций. Некоторые из этих функций включают в себя: преобразователь единиц, библиотеку констант, решатель уравнений, полиномиальный решатель, базовое преобразование и преобразование десятичного числа в дробное.

  Основные функции

  Дополнение

  Сложение (функция суммы) используется при нажатии кнопки «+» или с помощью клавиатуры. Функция дает a + b.

  Вычитание

  Вычитание (функция минуса) используется при нажатии кнопки «-» или с помощью клавиатуры.Функция приводит к a-b.

  Умножение

  Умножение (функция умножения) используется нажатием кнопки «x» или клавишей «*» на клавиатуре. Функция возвращает a * b. -1 или делению 1 на число.Икс. Числа автоматически отображаются в формате, когда число слишком велико или слишком мало для отображения. Чтобы ввести число в этом формате, используйте кнопку экспоненты «EEX». Для этого введите мантиссу (не экспоненциальную часть), затем нажмите «EEX» или введите «e», а затем введите показатель степени.

  Факториал

  Факториальная функция используется при нажатии «!» кнопку или введите «!».

  PI

  PI — математическая константа отношения длины окружности к ее диаметру.

  Тригонометрические функции онлайн

  синус

  Функция Sine (SIN) используется при нажатии кнопки «SIN» или вводе «SIN ()». Результат — отношение длины противоположной стороны к длине гипотенузы прямоугольного треугольника.

  Обратный синус

  Для использования функции обратного синуса (ASIN или ARCSIN) нажмите кнопку «ASIN» или введите «ASIN ()». Результат действителен только от -pi / 2 до pi / 2.

  Косинус

  Функция косинуса (COS) используется при нажатии кнопки «COS» или вводе «COS ()».В результате получается отношение длины соседней стороны к длине гипотенузы прямоугольного треугольника.

  Обратный косинус

  Функция обратного косинуса (ACOS или ARCCOS) используется нажатием кнопки «ACOS» или вводом «ACOS ()». Результат действителен только от 0 до пи.

  Касательная

  Функция тангенса (TAN) используется при нажатии кнопки «TAN» или типа «TAN ()». Результат — отношение длины противоположной стороны к длине смежной стороны прямоугольного треугольника.

  Обратная касательная

  Функция обратной тангенсации (ATAN или ARCTAN) используется при нажатии кнопки «ATAN» или при вводе «ATAN ()». Результат действителен только от -pi / 2 до pi / 2.

  Косеканс

  Функция косеканса (CSC) используется при вводе «CSC ()». Косеканс — это мультипликативная обратная функция синусоиды.

  Обратный косеканс

  Функция обратного косеканса (ACSC) используется при вводе «ACSC ()». Результат действителен только от -pi / 2 до pi / 2, исключая 0.

  Секант

  Функция секанса (SEC) используется при вводе «SEC ()». Секанс — это мультипликативная величина, обратная функции косинуса.

  Обратная секущая

  Функция обратного секанса (ASEC) используется при вводе «ASEC ()». Результат действителен только от 0 до pi, исключая pi / 2.

  Котангенс

  Функция котангенса (COT) используется при вводе «COT ()». Котангенс — это мультипликативная обратная функция касательной.

  Обратный котангенс

  Функция обратного котангенса (ACOT) используется при вводе «ACOT ()». Результат действителен только от 0 до пи.

  Онлайн-гиперболические тригонометрические функции

  Гиперболический синус

  Функция гиперболического синуса (SINH) используется при вводе «SINH ()».

  Гиперболический косинус

  Функция гиперболического косинуса (COSH) используется при вводе «COSH ()».

  Гиперболический тангенс

  Функция гиперболического тангенса (TANH) используется при вводе «TANH ()».

  Гиперболический косеканс

  Функция гиперболического косеканса (CSCH) используется при вводе «CSCH ()».

  Гиперболический секанс

  Функция гиперболического секанса (SECH) используется при вводе «SECH ()».

  Гиперболический котангенс

  Функция гиперболического котангенса (COTH) используется при вводе «COTH ()».

  Обратный гиперболический синус

  Функция обратного гиперболического синуса (ASINH) используется при вводе «ASINH ()».

  Обратный гиперболический косинус

  Функция обратного гиперболического косинуса (ACOSH) используется при вводе «ACOSH ()».

  Обратный гиперболический тангенс

  Функция обратного гиперболического тангенса (ATANH) Используется при вводе «ATANH ()».

  Обратный гиперболический косеканс

  Функция обратного гиперболического косеканса (ACSCH) используется путем ввода «ACSCH ()».

  Обратный гиперболический секанс

  Функция обратного гиперболического секанса (ASECH) используется путем ввода «ASECH ()».

  Обратный гиперболический котангенс

  Функция обратного гиперболического котангенса (ACOTH) используется при вводе «ACOTH ()».

  Меню

  Формат

  Доступно 4 типа числовых форматов, и формат можно изменить, нажав кнопку «Меню». Доступные типы чисел: стандартные, фиксированные, научные и инженерные. В инженерии можно выбрать количество цифр для отображения в поле ввода в строке формата.Используемый числовой формат можно увидеть над стеком, это третий статус меню слева. Это место можно щелкнуть, чтобы изменить числовой формат.

  Угол

  Доступно 3 типа представления углов, и эти типы углов можно изменить, нажав кнопку «Меню». Форматы углов: радианы, градусы и градиенты. Формат угла отображается над стеком и является первым статусом меню. На это место можно щелкнуть, чтобы изменить формат угла.

  Система координат

  Для представления комплексных чисел доступны две системы координат. Системы координат бывают прямоугольными и полярными. Систему координат можно выбрать, нажав кнопку «Меню». Выбранная система координат отображается над стеком и является вторым статусом меню. Чтобы ввести число в прямоугольном формате, его необходимо ввести в формате «(3,4)». Чтобы ввести число в полярном формате, его необходимо ввести в формате «(3 @ 75)».Вместо символа «@» можно использовать символ угла клавиатуры калькулятора.

  Режимы онлайн-калькулятора

  Есть два режима онлайн-калькулятора: Алгебраический и RPN. Режим выбирается нажатием на кнопку «Меню». Режим калькулятора отображается в четвертом индикаторе состояния меню, при нажатии на это место режим изменяется. Нижняя зеленая кнопка «возврат» или «=» изменяется в зависимости от режима.

  от десятичной дроби к дроби

  Функция преобразования десятичной дроби в дробь этого калькулятора позволяет представить десятичное число в дробных оценках, а также в точном эквиваленте дроби.Функция преобразования десятичной дроби в дробь активируется нажатием кнопки «d> f» (десятичная дробь в дробную) на клавиатуре калькулятора. Откроется дисплей в боковом поддоне с полем ввода вверху. Десятичное значение можно ввести непосредственно в поле ввода, или, щелкнув стрелку ввода, будет введено значение из поля ввода калькулятора.

  Комплексные числа

  Онлайн-калькулятор полностью поддерживает комплексные числа. Комплексные числа являются расширением системы действительных чисел и включают второе число, которое является воображаемым, создавая плоскость комплексных чисел.Числовой формат для комплексных чисел — «a + bi», где a — действительное число, а b — мнимое число. Эти числа также могут быть представлены как величина и угол, когда система координат калькулятора находится в полярном режиме.

  Онлайн-конвертер единиц

  Онлайн-конвертер единиц отображается на поддоне, и его можно выбрать, нажав кнопку «Единицы». Конвертер единиц имеет 11 категорий: масса, скорость, время, мощность, объем, площадь, длина, энергия, температура, сила и давление.

  Библиотека констант

  Библиотека констант — это функция поддона, доступ к которой можно получить, щелкнув кнопку «CONST». Чтобы поместить константу в поле ввода калькулятора, просто нажмите на константу. Эта библиотека содержит множество популярных констант, которые используются регулярно. Библиотека констант включает в себя следующее: скорость света, кулоновская постоянная, ускорение гравитации, гравитационная постоянная, постоянная Планка, постоянная Больцмана, постоянная Фарадея, масса покоя электрона, масса покоя нейтрона, масса покоя протона, число Авогадро, заряд электронов, радиус Бора. , Молярная газовая постоянная, постоянная Ридберга, молярный объем, диэлектрическая проницаемость вакуума, постоянная Стефана-Больцмана, квант магнитного потока, проницаемость вакуума, магнетон Бора, постоянная Джозефсона, импеданс вакуума и квант проводимости.

  Онлайн-решатель

  В онлайн-калькуляторе есть два часто используемых решателя. Доступ к этим решателям можно получить, щелкнув кнопку палитры «РЕШИТЬ». Доступные решатели: Линейный решатель и Корневой решатель.

  Линейный решатель

  Линейный решатель выбирается одним из 4 вариантов. Этот решатель позволяет решать для переменных, когда существует равное количество уравнений, уникальных для каждой неизвестной переменной.Решатель требует, чтобы были введены коэффициенты уравнений. При вводе номеров переменных убедитесь, что каждая запись в столбце используется для одной и той же переменной. Коэффициенты комплексных чисел могут быть введены, как только все значения введены, щелкнув по кнопке «Решить». Результаты помечены как x1 … xn. X1 соответствует переменной, используемой в столбце 1 и x2, столбце 2 и так далее.

  Решатель полиномов

  Решатель полиномов (решатель корня) выбирается щелчком по соответствующему порядку уравнения.Коэффициенты вводятся в поля ввода ниже. Затем нажмите «Решить», и результаты станут корнями уравнения.
  

  Базовый преобразователь

  Базовый преобразователь — это функция, которая включена в поддон, и к ней можно получить доступ, нажав кнопку «BASE».