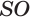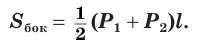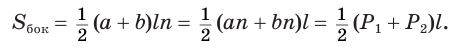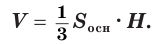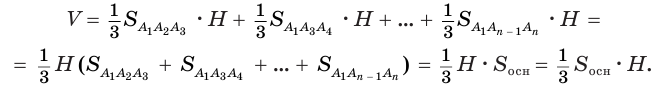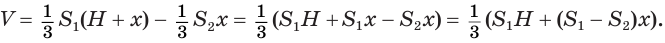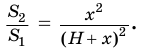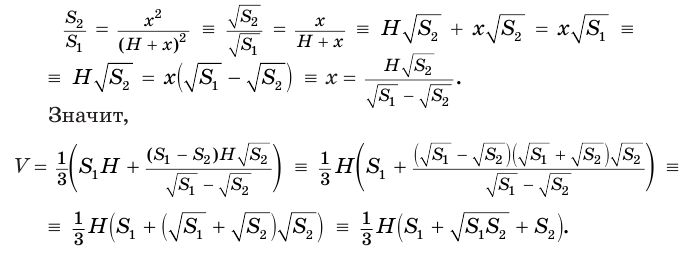Более тысячелетия египетские фараоны строили пирамиды и их хоронили под массивными памятниками или внутри них.
Египетские фараоны строили пирамиды между временем царя Джосера (годы правления 2630-2611 гг. до н.э.), построившего ступенчатую пирамиду в Саккаре, до времен царя Яхмоса I (годы правления 1550-1525 гг. до н.э.), построившего последнюю известную королевскую пирамиду в Египте..
Читай также: Более половины мужчин Европы — потомки Тутанхамона
Эти культовые пирамиды отображали силу, богатство фараонов и способствовали их религиозным убеждениям. Так почему же древние египтяне прекратили строительство пирамид вскоре после начала Нового царства?
В Древнем Египте строительство пирамид, казалось, пошло на убыль после правления Яхмоса, и вместо этого фараоны были похоронены в Долине царей недалеко от древнеегипетской столицы Фив, которая сейчас является современным Луксором. Theban Mapping Project отмечает на своем веб-сайте, что самая ранняя подтвержденная королевская гробница в долине была построена Тутмосом I (годы правления с 1504 по 1492 год до нашей эры). Его предшественник Аменхотеп I (годы правления 1525–1504 гг. до н.э.) мог также построить свою гробницу в Долине царей, хотя это является предметом споров среди египтологов.
Не совсем понятно, почему фараоны перестали строить королевские пирамиды, но соображения безопасности могли сыграть свою роль.
“Существует множество теорий, но, поскольку пирамиды были неизбежно разграблены, царские захоронения укрывались в далекой долине, высечены в скале и, предположительно, с множеством охранников некрополя, несомненно, сыграли свою роль“, — сказал Питер Дер Мануэлиан, профессор египтологии в Гарвардском университете.
Читай также: Стало известно, как возникли египетские пирамиды
“Еще до того, как они отказались от пирамид для королей, они перестали размещать погребальную камеру под пирамидой. У последней царской пирамиды — пирамиды Яхмоса I в Абидосе — была погребальная камера на расстоянии более 0,5 км за ней“, — сказал Эйдан Додсон, профессор египтологии Бристольского университета.
Одна историческая запись, которая может содержать важные подсказки, была написана человеком по имени Инени, который отвечал за строительство гробницы Тутмоса I в Долине царей. Инени писал, что “я руководил раскопками гробницы его величества один — никто не видел, никто не слышал“. Эта запись “очевидно предполагает, что секретность была главным соображением“, — сообщила Энн Мэйси Рот, клинический профессор истории искусства, иврита и иудаики Нью-Йоркского университета.
Естественный рельеф Долины царей может объяснить, почему она стала излюбленным местом для королевских гробниц. У него есть вершина, теперь известная как Эль-Курн (иногда пишется как Гурн), которая немного похожа на пирамиду. Пик “очень похож на пирамиду, [поэтому] в некотором смысле все королевские гробницы, построенные в долине, были помещены под пирамидой“, — сказал Мирослав Барта, египтолог, проректор Карлова университета в Чешской Республике. Э
Для египетских фараонов пирамида была важна, поскольку она была местом “вознесения и трансформации“ в загробную жизнь, писал Марк Ленер, директор и президент компании Ancient Egypt Research Associates, в своей книге “Полные пирамиды: разгадывая древние тайны“.
Читай также: Утерянный артефакт из египетской пирамиды нашли в коробке из-под сигар
Топография Луксора, который стал столицей Египта во время Нового царства (1550–1070 до н.э.), также мог сыграть роль в упадке строительства пирамид. По словам Додсона, этот район “слишком ограничен в пространстве, также здесь много холмов“. Другими словами, древняя столица могла быть слишком маленькой и сложной с архитектурной точки зрения, чтобы служить домом для новых пирамид.
Религиозные изменения, которые делали упор на строительство гробниц под землей, — еще одна возможная причина, по которой египтяне бросили грандиозные пирамиды. “Во времена Нового Царства очень популярной стала концепция ночного путешествия короля через Нижний мир, и для этого потребовались сложные планы гробниц, высеченных в скале под землей“, — сказал Барта. Подземные гробницы, высеченные в Долине царей, хорошо вписываются в эту концепцию.
В то время как фараоны перестали строить пирамиды, богатые частные лица продолжали эту практику. Например, гробница в Абидосе возрастом 3300 лет, построенная для писца по имени Хоремхеб, имела у входа пирамиду высотой 7 метров.
В течение первого тысячелетия до нашей эры строительство пирамид также стало популярным в Нубии, области, которая включает в себя нынешний Судан и некоторые части южного Египта. Нубийцы строили пирамиды как для королевской семьи, так и для частных лиц. Неясно, сколько они построили, Ленер в своей книге отметил, что существует около 180 королевских пирамид, в то время как недавние археологические исследования показывают, что было гораздо больше пирамид, построенных для частных лиц. Правители Нубии продолжали строить пирамиды примерно 1700 лет назад.
Напомним, ранее сообщалось, что разгадана еще одна тайна строительства пирамид в Египте.
Хотите знать важные и актуальные новости раньше всех? Подписывайтесь на Bigmir)net в Facebook и Telegram.
«Купи автомобиль мечты со скидкой до 70%», — предлагают авторы появившихся в Казани рекламных объявлений. Опрошенные «ВК» эксперты предупредили, что за предложением, от которого трудно отказаться, стоит очередная финансовая пирамида, что растут во время кризисов как грибы после дождя. Полиция пока что бездействует, ожидая заявлений от обманутых вкладчиков.
Увидев в лифте многоэтажки объявление купить задешево автомобиль мечты, корреспондент «ВК» зашел на сайт компании Sinergy Auto и узнал, что это целая международная группа компаний Synergy Group, работающая по «принципу кооперации для создания социально-экономических программ». Звучит красиво, но где-то мы подобное уже слышали…
Как выяснилось, компания берется помочь в сбыче практически любых ваших мечт. Схема такая: вносите в Synergy Group 29% от рыночной цены приглянувшейся вам машины, ждете 159 дней и получаете всю необходимую сумму на покупку авто. Если вносите 49% от цены — ждете всего 99 дней и получаете нужную сумму. То же самое с жильем. К примеру, приглянулась вам квартирка стоимостью 4 млн рублей, но таких денег у вас нет и вряд ли появятся. Не беда, говорят в Synergy Group: предлагают отдать им 1,4 млн и обещают, что через 145 дней сумма увеличится до 4 млн. Или, допустим, вам не хватает на шикарную свадьбу. Вы вкладываете отложенные на бракосочетание деньги, и через 90 дней вам возвращают вложения в двукратном размере.
— Откуда ж такая прибыль? — поинтересовался корреспондент «ВК», позвонив по указанному на сайте номеру.
Приветливая девушка по имени Ирина объяснила мне, что зарегистрированная в Новой Зеландии Synergy International Group Limited, с которой мне предстоит заключить договор, сотрудничает с известным хедж-фондом, который получит в доверительное управление мои кровные и приумножит их на биржевых торгах.
— А если что-то пойдет не так? Торги — дело рискованное, ищи вас потом в Новой Зеландии, — проявил я бдительность.
— Чтобы вы чувствовали себя защищенным во время ожидания, вам в качестве страховки предоставят криптовалюту на сумму, равную вкладу, — успокоила Ирина.
Как выяснилось, для спокойствия вкладчиков компания берется обеспечить их ларгокоинами (не путать с биткоинами). В ответ на мои вопросы Ирина также сообщила, что Synergy Group основана в прошлом году, офиса в Казани у компании пока нет, но планируется открыть, сейчас с потенциальными вкладчиками встречаются представители. Девушка также предупредила меня об условии, которое нужно выполнить для получения приумноженного капитала, — похвалиться удачным вложением в соцсетях. Кстати, на сайте самой компании уже представлен хвалебный отзыв от жительницы Казани, которая пишет, что благодаря вложению денег в Synergy Group смогла купить сыну дорогущий внедорожник Volkswagen Tiguan.
— Это стопроцентно финансовая пирамида! — прокомментировал «ВК» заманчивые предложения от новозеландской фирмы экономист, руководитель казанского центра разработки бизнес-планов «Позитив Консалтинг» Ирек Галямов. — По закону ни одна инвестиционная компания не может гарантировать доход. Если даже представить, что есть суперуспешный трейдер, который имеет грандиозную прибыль, то зачем ему вкладчики? Вложив тысячу долларов, он через два года станет миллионером, а через пять лет войдет в список «Форбс». То, что они предлагают в качестве страховки криптовалюту, очень похоже на схему, которую использовала действовавшая в Казани компания «Финико» (ее деятельность сейчас расследуется в рамках уголовного дела об организации финансовой пирамиды. — «ВК»). Подобные пирамиды сейчас появляются как грибы после дождя. Подобное происходит во время кризисов из-за падения покупательной способности населения, люди начинают верить в чудеса.
Такого же мнения и брокер ГК «Финам» Алексей Коренев:
— Если это не жулики, то они никогда не будут гарантировать вам высокую доходность. Хороший профессионал способен зарабатывать на рынке инвестиций, ценных бумаг 15 — 20 процентов годовых, не более. Все, что выше, должно вызывать подозрения. Возможно, кому-то они действительно заплатят обещанные деньги, но лишь для того, чтобы заманить в компанию новых клиентов. Страховка в виде криптовалюты — это смешно, так как криптовалюта в принципе ничем не обеспечена, это воздух. Криптовалют сегодня существует огромное количество, даже Бузова выпустила свою криптовалюту «бузкоин».
— Изучив образец договора на сайте компании, я бы категорически не рекомендовала вкладывать туда деньги, — предупредила в свою очередь казанцев юрист и арбитражный управляющий Мария Борисова. — Во-первых, смущает то, что компания якобы зарегистрирована в Новой Зеландии — мы не можем проверить, так ли это на самом деле. К тому же в договорах указано, что судебные споры рассматриваются по месту нахождения компании — то есть для защиты своих прав вкладчикам придется обращаться в новозеландский суд? На сайте компании нет информации о том, что у нее есть лицензия от Центробанка на право осуществления инвестиционной деятельности. Возможно, эта организация действует даже не по принципу финансовой пирамиды, когда старым вкладчикам выплачивают деньги за счет новых, а просто ничего не платит своим клиентам, мотивируя это тем, что доходов от инвестиций получить не удалось.
В пресс-службе Нацбанка РТ — отделении Банка России на вопрос «ВК» по поводу разворачивающейся в Казани деятельности Synergy Group ответили однозначно:
«Это так называемый партнерский проект финансовой пирамиды ANTARES, которой уже занимаются правоохранительные органы и Росфинмониторинг. Компания ANTARES LIMITED работала как через соцсети, так и в офлайне, были развернуты «консультационные центры» в нескольких регионах. Компания Synergy также имеет признаки финансовой пирамиды, Банк России передал информацию о ее деятельности в правоохранительные органы».
Но, похоже, информация до правоохранительных органов еще не дошла. В пресс-службе МВД по РТ на вопрос «ВК», не собирается ли полиция пресечь на корню деятельность крайне сомнительной организации, ответили, что займутся проверкой ее деятельности лишь после того, как поступят заявления от потерпевших.
Напомним, в конце прошлого года в Казани получили солидные сроки организаторы кредитно-потребительского кооператива «Рост». Они также обещали вкладчикам баснословную прибыль и пудрили мозги разговорами про выгодные инвестпроекты и игру на Американской фондовой бирже. В итоге кинули простаков на 1,4 млрд рублей.
1.
… вместе с ними в сумрак пирамид Живыми замуровывались жены. О, как жена, наверно, берегла При жизни …
Асадов Эдуард. Стихи и поэмы
2.
… в доме вдруг рухнула бы пирамида составленных вместе щитов. Я обхватила конюха руками и ногами — со …
Асприн Роберт. Артур-полководец 1-2
3.
… понял, что человек на верхушке пирамиды власти — создание людей ее дна или, по крайней мере, их …
Арчер Вадим. Выбравший бездну
4.
… описал фигуру на вершине Хеопсовой пирамиды, а потом, чтобы стать ближе к девушке, вспомнил свои гимназические …
Арцыбашев Михаил. Миллионы
5.
… храмов и пагод, вершины гордых пирамид, музыка любви, нежная ласка весенних вечеров и очарование лунных ночей …
Арцыбашев Михаил. Рассказы
6.
… Находясь в верхней части преступной пирамиды, он отвык от приемов и замашек уличной шантрапы. Даже «мясники … Бар «Оксиген» располагался в приземистой пирамиде. Раньше тут находился то ли банк, то ли чей-то …
Бурцев Виктор. Алмазный дождь
7.
… дело серьезное. И строится грандиозная пирамида. Я налил водки. — А вот паренек один представил мне другой … у шкафа, были составлены в пирамиду штурмовые винтовки М-28, лежали какие-то ящики в пятнах …
Бурцев Виктор. Алмазные нервы
8.
… за алтарем Вашанки, в виде пирамиды из камней, указывающей прямо на восток. Пот никогда не собирается …
Асприн Роберт. Мир воров 1-12
9.
… был оформлен в виде южноамериканской пирамиды; вход в него был копией Солнечных Врат Теотиуакана. Пройдя дальше … Вратам Конкистадоров с их усеченной пирамидой, яркими настенными росписями, знаменитыми испанскими ресторанчиками, «сельскими» танцорами, кружившимися под … из множества, ведущих на вершину пирамиды с плоской вершиной. Стискивая свои меч и кинжал, Люпус смотрел … причале номер 91 возвышалась приземистая пирамида из бочек с надписью: «ЧЕРНЫЙ ПОРОХ, ВЗРЫВООПАСНО!» Кто-то из … недалеко от него, рядом с пирамидой тяжелых бочек. Мгновение спустя детектив вынырнул из толпы обратно, побледнев …
Асприн Роберт. Вокзал времени 1-4
10.
… и нарастала, величественная, как египетские пирамиды. — В конце номера по моему сигналу врубишь радугу, — проговорил Бэнкс …
Асприн Роберт. Заклинание для спецагента
11.
… добыл бы себе приз на пирамиде кокосовых орехов. Полти выругался и с досадой пнул ваганский фургон …
Арден Том. Орокон 1-3
12.
… огнями, и огромные, как египетские пирамиды, горы земли, вывезенные из прорытых шахт, молчаливо упирались острыми конусообразными … как девчата-физкультурницы строили замысловатую пирамиду, Натка искоса разглядывала прибывших шефов. И вдруг на соседнем стуле … гарнизон. На уступах стен возвышаются пирамиды снежных снарядов. Между зубьями самодельный зеркальный перископ. В углу стоит …
Аркадий Гайдар. Рассказы и повести
13.
… из подсушенных «кирпичей» возводят усеченные пирамиды, каждая на два кубометра торфа. В этих-то пирамидах солнце … известью, которой отец пометит сложенные пирамиды торфапоставит на них кресты или первую букву своего имени. Тот …
Арагон Луи. Страстная неделя
14.
… торчал судьбы скелет Под хмарью пирамид над падалью зеленой Ветра носили шерсть и предсказанья бед Влюбленная …
Аполлинер Гийом. Стихи
15.
… достичь всего. Примеров тому множество — пирамида Хеопса, Суэцкий канал, Цимлянское море и т.д. — Наконец-то … до поднявшегося над землей орла. — Пирамиду! — заревел Медведь. — Быстро стройте пирамиду!.. Становитесь один на другого!.. Еще!.. Еще… Мгновенно образовалась пирамида в виде вертикальной лестницы. Медведь забрался по ней наверх и …
Априлов Борис. Приключения лисенка 1-2
16.
… подробно рассказывалась история этой финансовой пирамиды, держателем контрольного пакета акций которой был сам кучерявенький мэр. Юрий … тех, кто оказался под обломками пирамиды? Может быть, его иск к «Волгобанку» до сих пор пылится …
Арсеньева Елена. Безумное танго
17.
… отыскать описанный Страбоном вход в пирамиду Хеопса. Но и входа этого легендарного не сыскалось, и въезд … на картинах изображены не пустыня, пирамиды и сфинксы, а какие-то тесные, заросшие лесом пространства, извилистые … служили отнюдь не пустыня и пирамиды, а Зимний дворец в Петербурге. Точно! Академия художеств, Васильевский остров … был похоронен в солнечных часах. Пирамида, которая считается усыпальницей этого фараона, была построена с уклоном граней … метра ежедневно укорачивается тень от пирамиды — вплоть до своего полного исчезновения в день весеннего равноденствия — в …
Арсеньева Елена. Моя подруга — месть
18.
… читатель представит себе несколько трехгранных пирамид, положенных набок друг около друга, основанием в долину, а вершинами …
Арсеньев В.К.. По Уссурийскому краю
19.
… же, как и у египетских пирамид. Количество машин становилось все меньше, и улицы, в основном, были …
Арно Макс. Провокация
20.
… окном, превратив их в усеченные пирамиды. Народ на Студенческом бульваре оглянулся и уставился на пятый этаж … преисподней бани высилась огромная металлическая пирамида. Поговаривали, что она закрывает пуп земли, или, говоря научно — ее геомагнитный центр. Через пирамиду пролегали все окрестные туристические маршруты. Квелые туристы прислонялись животами к … узнать, кто и зачем построил пирамиду. Коренное население кивало то на военных, то на синоптиков, а … Академию наук. Очевидно было одно — пирамида вписывалась в ландшафт как природный объект. — Эти озера — самые чистые … видите, не успели мы обсудить пирамиду, как они тут же нарисовались. Они нас слышат. Меня, по …
Арсенов Яков. Избранные ходы
21.
… Алиса, они соединяли большую каменную пирамиду с камнями, установленными на дальних концах линий. — А что это там за пирамида? — поинтересовалась любознательная Алиса. — Это еще одна загадка долины Паско, — ответил компьютер. — Совершенно правильная пирамида. Но никто не смог найти в нее входа. Видно, древние … может быть, — предположила Алиса, — эту пирамиду построили пришельцы как памятник. Чтобы все знали, что они у … все, что ему попалось. Вот пирамида, вот полоски, вот камни… И на второй фотографии то же самое: полоски, пирамида, камни. Стоп! — сказала себе Алиса. Что-то неладно! Но что … хозяйка, и говорила: — Вот эта пирамида — вовсе не пирамида, а космический корабль, на котором прилетели камешки несколько тысяч лет … пор они ходят вокруг корабля-пирамиды и думают, что они на Земле одни. — Почему? — удивился академик …
Булычев Кир. Секрет черного камня
22.
… другое, образуя причудливую и неустойчивую пирамиду. Андрей подумал вдруг, что сейчас он может встретить отчима, который …
Булычев Кир. Река Хронос 1-2
23.
… рассаживались, делал вид, что любуется пирамидой салата, потому что хотел увидеть, куда сядет Гражина, и сесть …
Булычев Кир. Тринадцать лет пути
24.
… людей, как полковник Никольсон, воздвигались пирамиды, мосты и храмы. Такая воля побуждает умирающих людей работать с …
Буль Пьер. Мост через реку Квай
25.
… а одна, старая, похожая на пирамиду, встретила их у въезда в город. — Это Чианг Саен, — сказал …
Булычев Кир. Чума на ваше поле!
26.
… метрах от земли стволы расходились пирамидой, отсюда уже можно было спуститься без веревки. Крикнув наверх, чтобы …
Булычев Кир. Поселок
27.
… знаешь — отбор. Вот и получается пирамида. Те, кто на самом верху, имеют право — или несчастье — попасть … Их имена вырублены на склоне пирамиды буквами, соответствующими их репутации. Но внутри пирамиды, невидимые для глаз людских, таятся иные люди, может, не менее … править миром. Если снести вершину пирамиды, они появятся наружу, как дождевые черви, увиденные тобой, когда ты … светом прожекторов, стоят пулеметы и пирамиды винтовок. По лестнице спешат люди с красными повязками на рукавах …
Булычев Кир. Операция Гадюка
28.
… из рефрижератора, сказал, показывая на пирамиду: — Культовое здание. — Может быть, какое-нибудь учреждение. — На верхушке изображение …
Булычев Кир. Последняя война
29.
… В груде стекла валялся лом. Пирамиды консервных банок в витрине были разрушены, а изнутри, из темноты …
Булычев Кир. Рассказы
30.
… выросший вдесятеро, напоминающий одновременно египетскую пирамиду и китайскую пагоду Гордом, вот она — десятиэтажная статуя в центре … должен предупредить тебя, Слабенко, что пирамиды в Египте и колокольня Ивана Великого строились без башенных кранов … строения древности, в том числе пирамида Хеопса и Баальбекская веранда? — Все веранды дело рук человека, — отрезал … он, наше общество было подобно пирамиде. Наверху находился царь или генсек — не важно, как его называть … государства различных категорий. Была эта пирамида мафиозной, однако жила по строгим правилам. Если ты живешь в …
Булычев Кир. Рассказы о Великом Гусляре
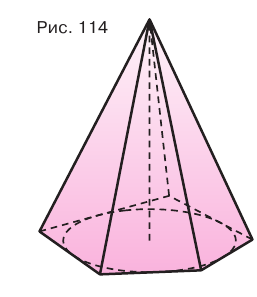
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
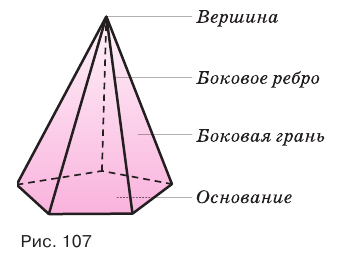
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
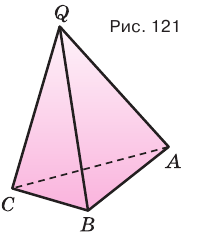
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
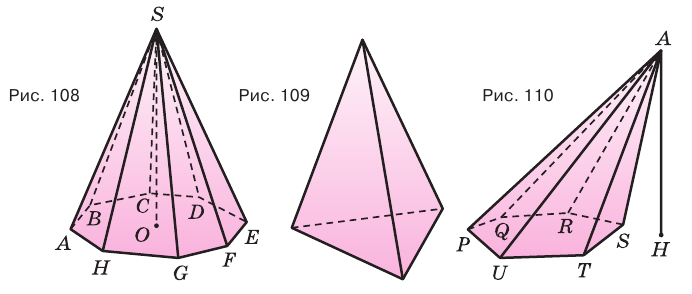
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
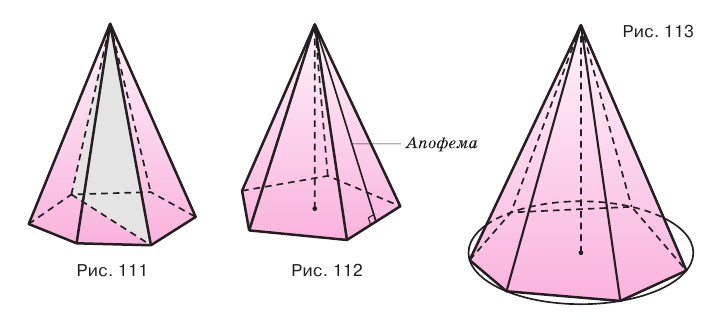
Отметим, что если в пирамиде равны все:
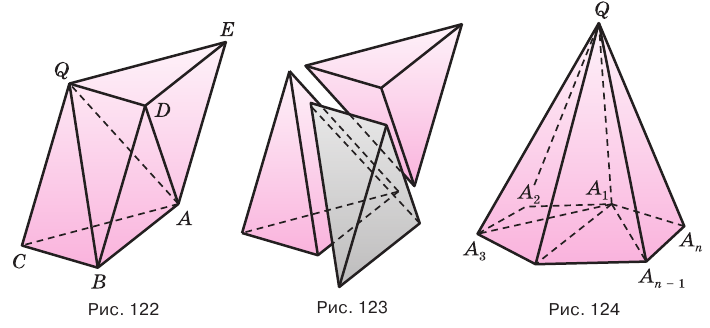
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
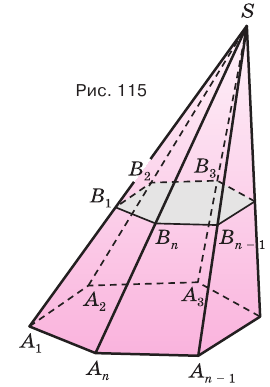
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
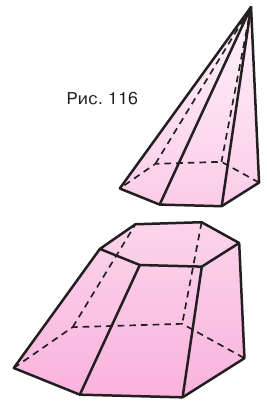
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
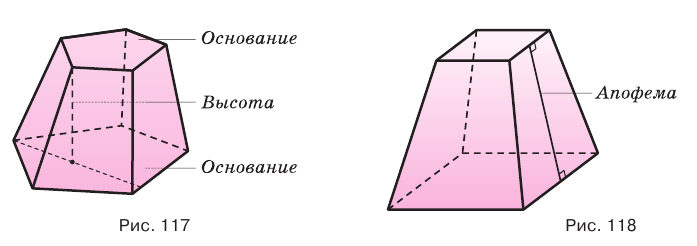
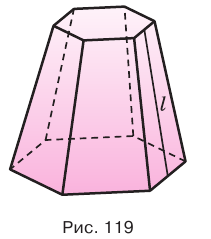
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 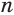
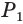
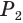
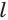
Боковая поверхность данной пирамиды состоит из 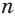
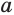
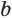
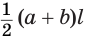
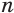
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
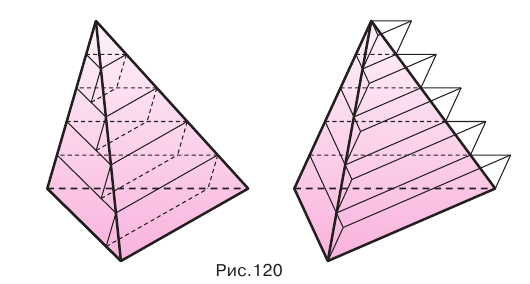
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 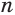
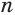
Пусть 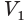
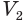


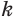
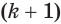


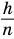
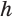
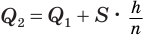
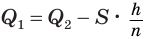
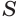
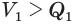
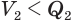
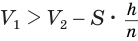
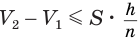
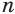
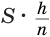
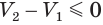
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 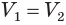
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

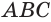
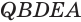
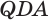


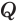
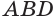
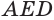




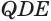

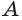
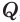





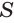

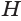



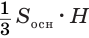
Пусть теперь есть произвольная пирамида 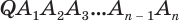
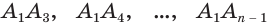
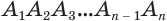
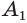
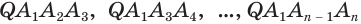

Пример:
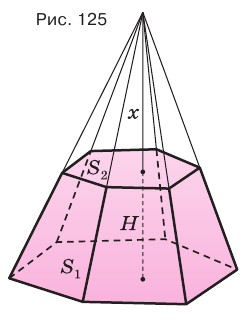
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 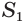
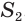

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 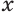
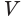
Чтобы найти высоту 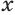
Решим это уравнение, учитывая, что 

Таким образом, объем 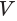
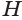


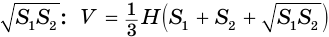
Статья из Википедии, бесплатной энциклопедии.
Эта статья о пирамидах как геометрических многогранниках. Для других значений, см Пирамида (значения) .
Н- односторонний пирамида (от древнего греческого πυραμίς / puramís ) представляет собой полиэдр образован путем соединения многоугольного основания из п сторон к точке, называемой вершиной , с помощью п треугольных граней ( п ≥ 3). Другими словами, это твердое тело конической формы с многоугольным основанием.
Если это не указано, предполагается, что основание квадратное. Для треугольной пирамиды каждая грань может служить основанием, а противоположная вершина — вершиной. Регулярный тетраэдр , один из многогранников , является треугольной пирамидой. Квадратные и пятиугольные пирамиды также могут быть построены с правильными гранями и, следовательно, являются телами Джонсона . Все пирамиды автодуальны .
Пирамиды — это подкласс призматоидов .
Происхождение названия
Слово «пирамида» происходит от древнегреческого πυραμίς, -δος / puramís, -dos, переданного на латынь в форме пирамида, -idis, но его происхождение неясно. Некоторые связывают это с понятием огня (греческий корень pyr ) и цитируют Платона, который видел в правильном тетраэдре (в форме пирамиды) символ огня. Другие считают, что это слово произошло от греческого « пурос », что означает « пшеница », напоминая, что это была форма королевских зернохранилищ. Другие до сих пор видят в этом искажение египетского слова « харам (или рем) », которое пишется на египетском языке hrm и которое является их именем на египетском языке, или слова « пр-м-ус », которое означает Египетская определяющая линия пирамиды. Наконец, другие отмечают, что слово « пирамида » по-гречески означало пирог из меда и муки.
Объем
Объем конуса , и , в частности , из пирамиды
где есть площадь основания и Н высота от основания до вершины, то есть перпендикулярно расстояние от плоскости , содержащего основание.
Перспективный вид геометрической пирамиды
В частности, объем квадратной пирамиды с высотой вершины, равной половине основания, можно рассматривать как одну шестую куба, образованного шестью такими пирамидами (в противоположных парах) через центр. Тогда «основание, умноженное на высоту» соответствует половине объема куба и, следовательно, трехкратному объему пирамиды, что дает коэффициент в одну треть.
Объем пирамиды с квадратным основанием, составленной из равносторонних треугольников, вдвое больше, чем у тетраэдра с той же стороны, что демонстрируется половинным разрезом .
Площадь поверхности
Площадь поверхности правильной пирамиды, то есть пирамиды, все грани которой являются идентичными равнобедренными треугольниками, равна
где A b — площадь основания, p — периметр основания и s — высота склона по биссектрисе грани (т. е. длина от середины любого края основания до ‘на вершине). .
Пирамиды с многоугольными гранями
Если все грани — правильные многоугольники, основание пирамиды может быть правильным многоугольником с 3, 4 или 5 сторонами:
Геометрический центр квадратной пирамиды расположен на оси симметрии, четверть основания к вершине.
Симметрия
Если основание правильное, а вершина находится выше центра, группа симметрии n- сторонней пирамиды будет C nv порядка 2 n , за исключением случая правильного тетраэдра, который имеет группу симметрии наибольшей T d порядка 24, в котором есть четыре версии C 3v для подгрупп.
Группа вращения — это C n порядка n , за исключением случая правильного тетраэдра, который имеет большую группу вращения T порядка 12, которая имеет четыре версии C 3 для подгрупп.
Обобщение на более высокие измерения
Пирамида — это геометрический объект, в основе которого лежит любой многоугольник, все вершины которого соединены в одну точку. Злоупотребляя языком, мы говорим, что он правильный, если все его грани являются правильными многоугольниками.
Обобщая, можно сказать , что гиперпирамида размерности 4 — это полихорус, имеющий в основе многогранник, к которому все его вершины соединяются в одну точку. Pentachore простейший пример.
Итак, n- мерная гиперпирамида — это n- мерный многогранник , который основан на n-1- мерном многограннике , и все вершины которого соединены с одной точкой. Гиперпирамиду можно рассматривать как совокупность всех «состояний», принятых ее основанием во время его постепенного сужения к вершине вдоль центральной медианы (соединяющей центр тяжести основания с вершиной); все эти «состояния» основания фактически являются пересечением гиперпирамиды с гиперплоскостями, параллельными основанию.
Гиперобъем гиперпирамиды размерности n определяется формулой:
где B n –1 — гиперобъем основания, h — высота.
Любой симплекс — это гиперпирамида, самая простая из всех измерений.
Примечания и ссылки
- ↑ Лексикографические и этимологические определения компьютеризированной «пирамиды» сокровищницы французского языка на сайте Национального центра текстовых и лексических ресурсов .
- ↑ a b и c Обен-Луи Миллен , Словарь изящных искусств , 1805, стр. 403 .
- ↑ Платон , Тимей [ подробности изданий ] [ читать онлайн ] , 56б.
- ↑ a и b Жан-Филипп Лауэр, «Пирамида», в Encyclopædia Universalis , 1990, T.19, p. 311 .
Смотрите также
Статьи по Теме
- Бипирамида
- Пирамида (архитектура)
- Пирамида (значения)
- Список пирамид во Франции
- Список современных пирамид
Внешние ссылки
- (ru) Равномерные многогранники
- (ru) Треугольная пирамида , квадратная пирамида и пятиугольная пирамида поочередно на сайте Math Is Fun
- (ru) Виртуальные многогранники , Энциклопедия многогранников , на сайте Джорджа У. Харта (en)
- Модели VRML (Джордж Харт) <3> <4> <5>
Геометрический портал