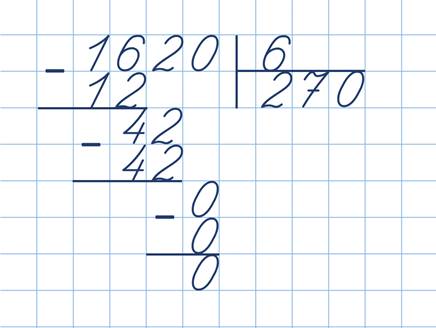Методический паспорт учебного проекта
Проект «Математические сказки»
Предмет: математика
Класс: 3В
Тип проекта: творческий, индивидуальная работа.
Планируемый результат: учащиеся научатся анализировать и сочинять математические сказки; оформлять свои мысли в устной и письменной речи, в том числе с применением ИКТ.
Цели:
-
Познакомить детей с математическими сказками.
-
Учить детей самостоятельно искать необходимую информацию.
-
Развивать творческие способности учащихся.
-
Анализировать и оценивать собственные творческие и деловые возможности.
Задачи проекта:
1. изучить литературу по данной теме;
2. использовать сказки на разных этапах урока;
3. привитие интереса к предмету математики;
4. включить учащихся в сочинительское творчество.
Гипотеза: Математика не является сухой и скучной наукой.
Практическая значимость: Можно использовать на уроках математики и во внеклассной работе.
Введение.
Уже давно сложился стереотип, что математика – скучная сухая наука. Но, я так не считаю. Математика – настоящее волшебное царство… А цифры, числа, геометрические фигуры, если к ним присмотреться повнимательнее, могут превратиться в удивительные сказочные персонажи. Любая тема преподносит нам такие интересные сюжеты, что самому ничего, и придумывать не нужно. Я решила оживить математику сказками. Математические сказки помогают поддержать интерес на уроке, развивают любознательность. Сказка позволяет привить вкус к самостоятельным рассуждениям, которые способствуют развитию математического мышления.
А что же такое сказка?
1. Что такое сказка?
В первую очередь, сказка – это жанр литературного творчества с установкой на вымысел. Причем сказка может быть как устной, так и письменной. Главной особенностью сказки является то, что это всегда выдуманная история со счастливым концом, где добро побеждает зло. Древняя Русь не знала слова «сказка». Вместо него служило слово «баснь». Баять – значит сказывать, рассказывать.
2. Какие бывают сказки?
Сказки бывают авторскими (сочиненные опредленнным автором) и народные (сочиненные многими людьми). Существует и другая классификация.
Сказки волшебные. В них раскрываются лучшие человеческие качества, герои романтичны. В такой сказке обязательно есть центральный положительный герой, его помощники и волшебные предметы. Герои волшебных сказок борются со злом и несправедливостью во имя добра и любви. В качестве примеров можно привести русские народные сказки про Ивана-дурака.
Сказки о животных. Здесь постоянные персонажи — это животные (лиса, волк, медведь, заяц и т.д.). Каждый из них олицетворяет то или иное человеческое качество, например, кот — умный, лиса — хитрая, медведь — сильный. Примеры: «Теремок», «Репка», «Колобок».
Бытовые сказки — иллюстрируют реальную жизнь, герои показаны с точки зрения их социального положения, высмеиваются отрицательные человеческие качества. Лучшими качествами в таких сказках обладают люди из народа, которые, как правило, оказываются умнее и хитрее представителей высокого социального статуса (господ, попов). Эти сказки — сатирические, в них много юмора и каламбура. Примеры социально-бытовых сказок: «Шемякин суд», «Каша из топора», «Барин и плотник», «Мужик и поп».
3. Чем отличается математическая сказка?
А что же такое математическая сказка?
Героями математической сказки могут быть: фигуры (треугольник, квадрат, прямоугольник и т. д.), цифры и числа. Кроме того героями математических сказок могут стать чертежные инструменты и письменные принадлежности — линейка, циркуль, ручки, карандаши. В содержание такой сказки обязательно закладывается математическое понятие или свойство.
4. Урок.
Я решила оживить математику и представила задачи в виде сказок. Решение задач с необычными сюжетами способствует развитию интереса учащихся к математике, повышает их активность на уроке, предотвращает психическую усталость однообразной деятельностью.
• Однажды Пятачок уехал в гости к бабушке, а Винни-Пух всё это время сидел дома один. Пока он сидел дома, съел 12 кг мёда, а когда Пятачок вернулся и пришёл к Винни-Пуху, они съели на 6 кг больше, чем Винни-Пух один. Сколько кг мёда всего съели друзья?
• Винни — Пух и Пятачок пошли в гости к Кролику. Они шли по тропинке, которая вела через лес. Тропинка состояла из 4 частей. Первая часть была длиной 14 м. Вторая часть была на 2 м. больше первой. Третья часть была на 8 м. меньше второй. Четвёртая часть была на 7 м. больше третьей. Какова длина дороги?
• Когда Винни-Пух и Пятачок пришли к Кролику, он предложил гостям чай с вареньем. Кролик съел 1 кг варенья. Пятачок съел на 3 кг больше, чем Кролик. Винни-Пух съел на 2 кг больше, чем съели Кролик и Пятачок вместе. Сколько кг варенья съел Винни-Пух?
• Когда Винни-Пух и Пятачок собрались уходить домой, Винни-Пух застрял в двери. Чтобы пройти в дверь, нужно весить 13 кг, а Винни-Пух весил 16кг. На сколько килограммов нужно похудеть Винни-Пуху, чтобы пройти в дверь?
• Мама попросила Красную Шапочку отнести бабушке пирожки. Она понесла бабушке 16 пирожков, но по пути она отдала волку 6 пирожков, а сама съела в 2 раза меньше, чем Волк. Сколько пирожков осталось для бабушки?
• Когда Колобок убежал от бабушки с дедушкой, он покатился по тропинке, которая вела сначала через лес, потом через поле и через луг. Через лес Колобок катился 14 м. Через поле на 6м больше. Через луг на 4 м меньше, чем через лес и поле вместе. Какова длина тропинки?
• Через 15 минут от начала пути Колобок встретил зайца. Через 7 минут волка, спустя 9 минут медведя. Сколько времени в пути был Колобок?
Работа над проектом
1этап. Подготовительный.
Сообщение цели и задач проекта. Создать презентации.
2 этап. Планирование и организация деятельности.
Сбор материала.
Оформление работы.
Защита.
3 этап. Исследование (осуществление деятельности, выполнение работы)
Оформляют работы.
4 этап. Представление результатов, отчёт.
-
Представление и защита работ.
-
Оценивают свою работу и работы своих одноклассников.
Заключение.
Я думаю, что у меня получилось заинтересовать ребят. Я показала им, что математика совсем не скучная наука. Решение задач с необычными сюжетами способствует развитию интереса учащихся к математике, повышает их активность на уроке.
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Презентация к уроку математики «Деление столбиком», 3 класс
Урок математики
в 3 классе
Здравствуй, дорогой друг!
Эта презентация поможет тебе разобраться с новой темой. А какой ты узнаешь проходя каждое задание!
Желаю удачи!
Реши примеры в тетради:
7 * (14 + 27) =
(36 – 12) * 22 =
(120 : 20) * 52 =
2 : (104 – 52) =
— Какой пример оказался для тебя трудным?
— Почему именно в этом примере у тебя возникло затруднение при решении?
Тема урока:
«Деление в столбик»
— Для начала давай вспомним компоненты деления!
Запомни!
Алгоритм деления в столбик.
1. Записываем пример столбиком.
2. Ищем первое неполное делимое.
3. Считаем, сколько цифр будет в частном.
4. Делим неполное делимое.
5. Проверяем умножением.
6. Ищем остаток (он должен быть меньше делителя)
7. Сносим следующую цифру. Делим, проверяем умножением, ищем остаток и так, пока не разделим делимое.
8. Читаем ответ.
Потренируемся!
Реши задачи в тетради.
Задача 1. В 9 почтовых ящиков разложили 18 газет поровну. Сколько газет положили в каждый почтовый ящик?
Решение: 18 : 9 = 2 (г)
Ответ: По 2 газеты положили в почтовые ящики.
Задача 2. 24 апельсина раздали детям по 3 штуки каждому. Сколько детей получили апельсины?
Решение: 24 : 3 = 8 (д)
Ответ: 8 детей получили апельсины.
Возникли ли у тебя трудности при решении задач?
В этих задач мы использовали табличные случаи деления!
А теперь давай решим в тетради еще одну задачу.
Задача 3. В одной книге 65 страниц, а во второй в 5 раз меньше. Сколько страниц во второй книге?
— Сможем ли мы так же быстро решить эту задачу, как и прежние? Почему?
- Верно! Так как в таблицы умножения нет такого примера.
- Значит, нам нужно будет делить эти числа столбиком!
1. Сначала мы запишем пример: 65 : 5 =
2. Ниже мы будем записывать его решение в столбик:
5 1 3
15
15
3. Записываем ответ в пример выше.
4. Записываем ответ к задаче: 13 Страниц во второй книге.
Теперь попробуй решить задачи самостоятельно в тетради:
Задача 4. На овощебазу привезли 69 мешков моркови, а мешков с картошкой в 3 раза меньше. Сколько мешков картошки привезли на овощебазу?
Решение:
69 : 3 =
6
9
9
23
2 3
Ответ: 23 мешка картошки привезли на овощебазу.
Домашняя работа.
Реши задачи в тетради используя деление в столбик.
Задача 1. Одна машина проехала 84 км, а вторая в 4 раза меньше. Сколько километром проехала вторая машина?
Задача 2. За неделю Петя прочитал 93 страницы, а Вася в 3 раза меньше. Сколько страниц прочитал Вася?
Спасибо за урок!
Конспект урока математики Деление на однозначное число, 3 класс, ФГОС, ОС Перспектива. Автор: Л. Г. Петерсон.
Конспект урока математики «Деление на однозначное число»,3 класс, ФГОС,ОС «Перспектива».
Автор: Л. Г. Петерсон.
Конспект урока подготовила Дударева Надежда Михайловна, учитель начальных классов МБОУ «Средняя общеобразовательная школа № 22» г. Калуги.
Тема урока: Деление на однозначное число
Тип урока: урок изучения нового материала (продолжение)
Цель: построение модели нового способа деления на однозначное число
Задачи:
+образовательные
— сформирование умения делить числа столбиком
+развивающие
— развивать мышление, грамотную математическую речь, интерес к урокам математики;
УУД:
*регулятивные
— осознание учащимися того, что уже усвоено и что ещё нужно усвоить;
— развивать контроль и самоконтроль при проверке заданий;
— планировать свои действия в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане;
— оценивать правильность выполнения действия на уровне адекватной оценки соответствия результатов требованиям данной задачи и задачной области.
*познавательные
— совершенствовать вычислительные навыки;
— развивать умение извлекать информацию;
-перерабатывать полученную информацию: сравнивать и группировать математические факты;
— делать выводы на основе обобщения умозаключений;
+коммуникативные
-адекватно использовать коммуникативные, прежде всего речевые, средства для решения различных коммуникативных задач, строить монологическое высказывание
-учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
-формулировать собственное мнение и позицию;
-использовать речь для регуляции своего действия;
+воспитательные
— воспитание аккуратности при работе в тетрадях.
Оборудование:
— учебник;
— презентация;
Ход урока
1.Организационный момент
-Сейчас у нас урок математики.
— У вас на столе должны быть: учебник, тетрадь и пенал.
3.Проверка домашнего задания
2.Актуализация имеющихся знаний
-С каким новым способом деления мы с вами знакомились на предыдущем уроке?
— Мы познакомились с делением чисел в столбик.
— А как мы считали до того, как узнали, как делить столбиком?
— Мы сначала делили сотни, потом десятки ,затем единицы и все складывали.
— Откройте тетради, подпишите число и классная работа.
-Попробуем решить такой пример этим способом — 675:3
-Делим сотни 5 с. :3= 2с.
-Делим десятки 7д.:3= 2д. (ост.1 д.)
-Делим единицы 15 ед. :3 = 5ед.
-Какой у нас получился ответ?
— У нас получился ответ 225.
— каким способом можно ещё решить этот пример?
— Деление уголком.
— Давайте с вами повторим алгоритм деления .
-Что нужно сначала сделать, чтобы разделить числа углом?
— Нам нужно найти неполное делимое.
-Верно. Какой у нас следующий шаг ?
— Мы должны определить число цифр в частном.
— А затем что мы делаем?
— Мы решаем пример и находим ответ.
Решим пример 675 : 3 столбиком.
-Я пишу пример на доске, а вы мне помогайте, чтобы у нас получился верный ответ.
— Ребята ,что я сначала должна сделать?
— Выделить неполное делимое.
— Какое у нас в этом примере будет неполное делимое? Почему?
— В этом примере неполное делимое будет 6,так как 6 делится на 3.
— Верно. Какую цифру я должна написать в частное? Почему?
— Цифру 2, так как 6 разделить на 3 будет 2.
-Значит ,я из 6 вычитаю 6 и получается 0,а 0 мы не пишем. Какое число мы сносим?
— Мы сносим число 7.
Число 7 делится на 3?
-Нет.
-Какое число будет ближайшее к числу 7, которое делится на 3?
— это число 6.
Значит, что мы делаем?
— Мы в частное пишем 2, а из семи вычитаем 6 и получится остаток 1
— Хорошо. Какое число нам осталось снести?
-Это число 5.
— 15 у нас делится на 3?
— Да, делится.
— Какую цифру я должна написать в частное? Почему?
-Цифру 5. Так как 3 умножить на 5 будет 15.
-Верно ребята. Деление у нас закончено?
— Да.
— Какой ответ у нас получился?
— Унас получился ответ 225.
— Сравните его с предыдущим ответом ,когда мы делили отдельно сотни, десятки ,потом единицы.
-Эти ответы совпадают?
— Да, совпадают. Значит, мы верно решили пример в столбик.
— Мы справились с этим примером. Нашли верный ответ.
3. Первичное закрепление.
Теперь откроем учебник на странице 13. Найдите номер 1.
Эти примеры мы будем решать у доски по « цепочке».
-При решение примеров пользуемся алгоритмом деления.
-Приступаем к работе. ( дети по очереди выходят к доске, решают примеры с комментированием по алгоритму)
Перейдем с вами к заданию №4. Прочитаем задание (читает один из учащихся.)
Решение устно под цифрой 1. Ребята смотрим с вами первый вариант :а -=0 ,b= 1. Вспоминаем правило при умножении на ноль.
— Если число умножить на ноль ,то получится 0.
— А если мы число делим на единицу, то что у получится?
— Если число разделить на единицу, то получится данное число.
— Теперь подставляем вместо b- единицу вместо а — 0. Какое выражение у нас получилось?
— 6309*0 + 936:1.
— Какой ответ у нас получится?
— Ответ будет 936.
— Верно. Смотрим пример под цифрой 2. Запишем его с подстановкой чисел вместо а и b . Какое выражение получилось?
— 6309 *6+936:2
Расставьте действия.
— Как удобнее нам посчитать первое действие: 6309 *6?
— Удобнее посчитать столбиком.
— Верно. Решаем в тетради самостоятельно . Какой ответ получился?
— Ответ в этом действии 37854.
— Какое действие будет вторым?
— Второе действие 936:2.
— Как лучше вычислять ?
— Удобнее вычислять столбиком ( вызываю одного ученика к доске, остальные пишут в тетради)
— Проверьте, правильно ли решил(-ла) (имя ученика) этот пример.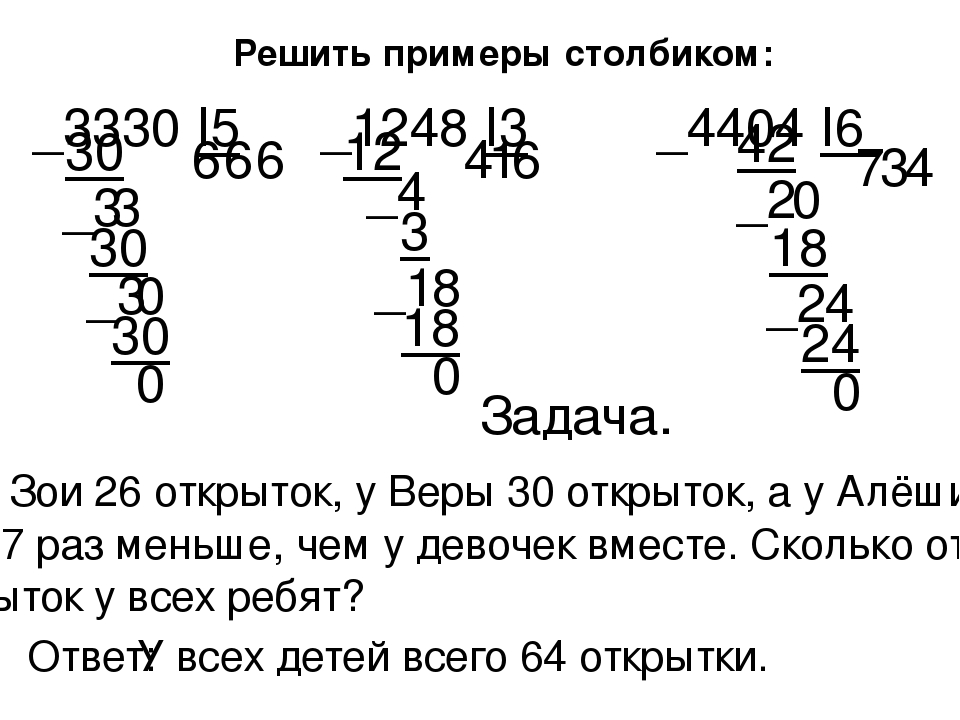
— Ответ 468.
— теперь что нам нужно сделать?
— Нам нужно сложить первое и второе действие
— решите самостоятельно. Скажите мне ответ.(38322)
4.Физкультминутка
Мы решали, мы решали
Мы решали, мы решали.
Что-то очень мы устали.
Мы сейчас потопаем, (Шаги ногами на месте под счет учителя.)
Ручками похлопаем. (Хлопки в ладоши.)
Раз присядем,
(Приседания.)
Быстро встанем, (Повороты туловища. Ходьба на месте.) Улыбнемся, Тихо сядем.
5. Вторичное закрепление.
Посмотрим на страницу 14 №8. Решим этот номер устно.
Для выполнения этого номера повторим единицы измерения длины и массы. (написано мелом на доске.)
см дм м км
г ц кг т
Соедините дужками и подпишите . сколько в сантиметре дециметров, в дециметре метров и т.
Теперь приступаем к решению задания при этом обосновывая свою точку зрения( дети объясняют с пояснением почему одна единица измерения больше или меньше другой)
Пример: 45см будет меньше 2 м,так как в 2 м =200см,а 200 больше, чем 45,значит 45см будет меньше чем 2 м. И так оставшиеся примеры.
6. Домашнее задание.
Наш урок подходит к концу.
-Запишите домашнее задание. Стр13-14 ,№ 2,5а),6
7. Итог урока.
— Что мы сегодня узнали на уроке?
— Что было для вас трудным?
— Понравился ли вам урок?
-Чему вы научились на уроке ?
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/125209-konspekt-uroka-matematiki-delenie-na-odnoznac
Таблица деления (математика для детей, 2, 3 класс)
На 1
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 1 = 3
4 ÷ 1 = 4
5 ÷ 1 = 5
6 ÷ 1 = 6
7 ÷ 1 = 7
8 ÷ 1 = 8
9 ÷ 1 = 9
10 ÷ 1 = 10
На 2
2 ÷ 2 = 1
4 ÷ 2 = 2
6 ÷ 2 = 3
8 ÷ 2 = 4
10 ÷ 2 = 5
12 ÷ 2 = 6
14 ÷ 2 = 7
16 ÷ 2 = 8
18 ÷ 2 = 9
20 ÷ 2 = 10
На 3
3 ÷ 3 = 1
6 ÷ 3 = 2
9 ÷ 3 = 3
12 ÷ 3 = 4
15 ÷ 3 = 5
18 ÷ 3 = 6
21 ÷ 3 = 7
24 ÷ 3 = 8
27 ÷ 3 = 9
30 ÷ 3 = 10
На 4
4 ÷ 4 = 1
8 ÷ 4 = 2
12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10
На 5
5 ÷ 5 = 1
10 ÷ 5 = 2
15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10
На 6
6 ÷ 6 = 1
12 ÷ 6 = 2
18 ÷ 6 = 3
24 ÷ 6 = 4
30 ÷ 6 = 5
36 ÷ 6 = 6
42 ÷ 6 = 7
48 ÷ 6 = 8
54 ÷ 6 = 9
60 ÷ 6 = 10
На 7
7 ÷ 7 = 1
14 ÷ 7 = 2
21 ÷ 7 = 3
28 ÷ 7 = 4
35 ÷ 7 = 5
42 ÷ 7 = 6
49 ÷ 7 = 7
56 ÷ 7 = 8
63 ÷ 7 = 9
70 ÷ 7 = 10
На 8
8 ÷ 8 = 1
16 ÷ 8 = 2
24 ÷ 8 = 3
32 ÷ 8 = 4
40 ÷ 8 = 5
48 ÷ 8 = 6
56 ÷ 8 = 7
64 ÷ 8 = 8
72 ÷ 8 = 9
80 ÷ 8 = 10
На 9
9 ÷ 9 = 1
18 ÷ 9 = 2
27 ÷ 9 = 3
36 ÷ 9 = 4
45 ÷ 9 = 5
54 ÷ 9 = 6
63 ÷ 9 = 7
72 ÷ 9 = 8
81 ÷ 9 = 9
90 ÷ 9 = 10
На 10
10 ÷ 10 = 1
20 ÷ 10 = 2
30 ÷ 10 = 3
40 ÷ 10 = 4
50 ÷ 10 = 5
60 ÷ 10 = 6
70 ÷ 10 = 7
80 ÷ 10 = 8
90 ÷ 10 = 9
100 ÷ 10 = 10
(на 0 делить нельзя)
Учить таблицу деления — игра
Математическим действием, которое противоположно умножению, называется деление.
Таблица деления в виде картинки
Чтобы распечатать, скопируйте картинку в любой редактор. Обычно таблицу деления дети проходят на математике в третьем классе.
Открыть в отдельном окне в полном размере
Деление онлайн
/
Посмотрите также видео о делении в столбик.
Таблица деления для этого может пригодиться.
Всё для учебы » Математика в школе » Таблица деления (математика для детей, 2, 3 класс)
Тема урока: «Деление круглых чисел» 3 класс
Тема: «Деление круглых чисел».
Тип урока: ОНЗ.
Основные цели:
1) формировать умение делить числа оканчивающиеся нулями;
2) актуализировать приёмы деления многозначного числа на однозначное и деление на 10, 100 и 1000;
3) тренировать навыки решения задач.
.
Ход урока:
-
Мотивация к учебной деятельности:
На доске ( презентация)
— Вы узнали кто это? (Да, это Баба-Яга)
— Немецкий писатель Отфрид Пройслер написал повесть-сказку, которую назвал «Маленькая Баба-Яга». Не правда ли странно Баба-Яга и маленькая.
— Докажите, что высказывание известного писателя Максима Горького подходят к стремлениям героини сказки.
« Всегда – учиться, все – знать! Чем больше узнаешь, тем сильнее станешь» (М. Горький)
(Чем больше училась маленькая Баба-Яга, тем она становилась сильнее, настоящей ведьмой)
— А можно ли их отнести к вам? (Да, чем больше мы узнаем, тем сильнее станем в своих знаниях…)
— А вы хотите стать сильнее? (Да)
— Как связаны эти слова с нашим уроком? (Мы узнаем, что-то новое и станем сильнее в своих знаниях.)
— Как вы узнаете, что-то новое? (Сначала мы должны понять, что мы не знаем, а потом сами найдем способ)
— Чему вы научились на предыдущих уроках? (Мы научились делить столбиком.
— Все ли вы знаете о делении в столбик? (Нет, мы знаем не все)
— Как вы думаете, чему будет посвящен урок? (Мы узнаем что-то новое про деление?)
Вывешивается часть темы: слово «Деление…»
— Ребята, как обычно строится работа на уроке, когда мы находим что-то новое. (Сначала мы повторим необходимое, потом попробуем выполнить задание на пробное действие )
2. Актуализация знаний и фиксация затруднений в пробном учебном действии.
Организация учебного процесса на этапе 2:
-
Повторение:
– Маленькая Баба-Яга приготовила для вас несколько заданий, я уверена вы легко с ними справитесь:
Устный счет: 25х4:10х40:100х50:10х300:1000х5= ?
— У кого получился такой же ответ(30) напишите на пустой бересте букву «А».
— С первым заданием вы успешно справились. Чем будете пользоваться при выполнении второго
задания?
20800 :100; 560000 : 1000; 802000 :1000; 7030000 :100
(Для выполнения этого задания нам потребуется правило и опорная схема
деления числа на 10, 100 и 100.)
Дети работают в парах. Проверка проводит-
ся фронтально.
— Кто выполнил задание правильно, напишите на бересте букву – «Б», у кого не получилось – «?».
– Еще одно задание:
2070 : 9 1016 :8
— Кто правильно решит первый пример, тот узнает, сколько лет маленькой Бабе–Яге. Кто правильно решит второй пример, тот узнает, до какой страницы колдовской книги дошла маленькая Баба-Яга.
— Чем будете пользоваться при делении? (Мы будем пользоваться алгоритмом деления многозначного числа на однозначное углом).
Один ученик работает у доски, он объясняет ход решения (остальные выполняют деление в тетради). Дети сравнивают свои ответы с ответами на доске.
— Сколько же лет маленькой Бабе-Яге? (127лет.) До какой страницы колдовской книги дошла маленькая Баба-Яга. (До 230 страницы.) О чем это говорит, как вы думаете; Бабе-Яге 127лет, а дошла она всего до 230 страницы? ( …..)
— Вы справились с заданием и получаете еще одну букву — «Р».
2) Пробное действие:
— Итак, что мы с вами повторили? (Деление в столбик, деление на 10, 100, 1000 и свойство деления: при делении делимого и делителя на одно и то же число результат частного не изменится.)
— Какое задание вы сейчас получите? (Задание, в котором есть что-то новое.
— Докажите что вы готовы его получить. (Мы готовы, так как задания на повторение мы выполнили правильно.)
Учитель вывешивает задание для пробного действия
371000 :700
-
Что нового в этом задании? (Нужно найти частное чисел, когда делимое и делитель являются круглыми числами.)
-
Какую цель мы поставим перед собой на этом уроке? (Научиться делить круглые числа.)
-
Сформулируйте тему урока? (Деление круглых чисел.)
-
Попробуйте выполнить это задание.
Задание выполняется самостоятельно на время — 1–2 минуты.
-
Что показало ваше пробное действие? (Мы не смогли разделить 371 000 на 700.)
-
У кого есть ответ?
Учитель записывает возможные варианты ответов на доске.
-
Каким правилом или алгоритмом воспользуетесь, чтобы определить, кто прав.
(Такого правила у нас нет.)
-
Что показало ваше пробное действие? (Мы не можем обосновать правильность своего решения, у нас нет алгоритма.)
3. Выявление места и причины затруднения.
Организация учебного процесса на этапе 3:
-
Какое задание вы выполняли? (Находили частное чисел 371 000 и 700.)
-
Каким эталоном вы пытались воспользоваться? (Алгоритмом деления многозначного числа на однозначное.)
-
В чем возникло затруднение? (Мы делили на трехзначное круглое число, а у нас алгоритм для деления на однозначное число.)
-
Расскажите, опираясь на этот алгоритм деления, как вы действовали. И назовите место, где вы засомневались. Что вы при этом подумали? (…Затруднение возникло на первом шаге: не понятно, что делать с нулями при определении первого неполного делимого, считать ли их при определении количества цифр в частном? …)
-
Почему возникло затруднение? (У нас нет алгоритма деления круглых чисел.
)
4. Построение проекта выхода из затруднения.
Цель:
-
поставить цель проекта,
-
определить средства для построения нового знания,
-
сформулировать шаги достижения поставленной цели.
Организация учебного процесса на этапе 4:
-
Какую цель нам надо поставить перед собой? («Открыть» алгоритм деления круглых чисел.)
-
Какая тема нашего урока? (Деление круглых чисел.)
-
Какой следующий шаг? (Мы должны составить план выхода из затруднения)
-
Вам необходимо построить способ решения таких примеров. На что будете опираться (какие средства использовать)? (Эталон деления на 10, 100, 100; свойство деления на одинаковое число; эталон деления на однозначное).
-
Какой будет план вашей работы? Дети называют шаги плана, учитель вывешивает или записывает их на доске, затем коллективно корректируют порядок шагов.
1.Продумать шаг, приводящий к делению на однозначное число.
2.Выполним деление углом.
4.Сделаем вывод.
5. Реализация построенного проекта.
Цель:
1) создать условия для построения детьми нового способа решения примеров деления круглого с остатком;
2) применить новый способ действий для решения примеров, вызвавших затруднение;
3) зафиксировать новый способ действия в речи и с помощью эталона;
4) зафиксировать преодоление возникшего затруднения.
Организация учебного процесса на этапе 5:
Дети, работая по плану, получают у себя в тетрадях запись:
371000 : 700 = (371000 : 100) : (700 : 100) = 3710 : 7 = 530
3710 | 7 .
35 530 700 .
21 371000
21
Один ученик объясняет решение на доске, остальные проверяют свою работу.
— Какой вывод вы сделали? (При делении на 100 мы отбросили одинаковое количество нулей в делимом и делителе, а затем воспользовались алгоритмом деления многозначного на однозначное. Значит нам надо добавить один шаг в алгоритм деления углом.)
Д
Мысленно разделить делимое и делитель на одно и то же число, зачеркнуть поровну нулей.
ети вывешивают на доску свои варианты, например:
Мысленно отбросить в делимом и делителе поровну нулей.
Зачеркнуть (отбросить) одинаковое количество нулей в делимом и делителе.
Все вместе выбирают лучший. Учитель может предложить свой Д-13 прикрепляется. Аналогично разбираются эталоны. В результате на доске Д-14.
-
Куда прикрепить дополнительный шаг? (В начало алгоритма, с этого шага мы начнем деление круглых чисел.
) Учитель прикрепляет к началу алгоритма дополнительный шаг.
-
Вы довольны работой? (Да)
-
Что должны делать дальше? (Потренироваться в решении примеров с применением полученного нами нового алгоритма и эталона)
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
создать условия для выполнения учащимися типовых заданий на использование изученного способа действия с проговариванием во внешней речи.
Организация учебного процесса на этапе 6:
-
– Это задание находится в учебнике на стр. 25 № 3 третий столбик.
Один ученик работает у доски, остальные в тетрадях, используя алгоритм, выполняет деление
632 160 : 40. (Отброшу в делимом столько нулей, сколько их в делителе (один нуль). Буду делить
63 216 на 4. Действуя по алгоритму деления многозначного на однозначное, узнаю частное 15 804.
На доске и в тетрадях запись:
6
/ / / / / /
32 160 : 40 = 15 804 184200 : 600 = 307 Проверка: X 307
63216 | 4 Проверка: X15804 1842 | 6 600
4 15804 40 18 307 184200
23 632160 42
20 42
32 0
32
016
16
2) стр.25 № 3 (4 столбик)
— Как будете работать дальше? (В парах. Каждый «попробует» свои силы в применении алгоритма: первый пример – 1 вариант проговаривает второму варианту, 2 пример – 2 варианта проговаривает первому). Пробуйте…
— Кто за 3 минуты успеет выполнить задание, в оставшееся время решает первый пример 1столбика.
— Время закончилось. Теперь что нужно сделать? (Проверить по подробному образцу на доске).
— Если вы правильно решили, пишите букву «А», если неправильно — ?.
– Проверьте записи в своих тетрадях с соответствующим образцом (образец решения вы найдёте на своём столе).
— Кто не успел выполнить задание? Кто допустил ошибки? В чём ошибся? По какой причине?
— Какой наш следующий шаг вашей работы? (Теперь нужно поработать самостоятельно).
7. Самостоятельная работа с самопроверкой по эталону.
Организация учебного процесса на этапе 7:
– Над домиком маленькой Бабы-Яги сгустились тучи, но она забыла заклинание. Давайте поможем разогнать тучи. Выберите примеры, которые можно решить с помощью нового алгоритма и запишите их в тетрадь.
– Сколько туч осталось? (Две: 71 200 : 20, 3 270 000 : 300) Учитель убирает лишние тучи-примеры.
Решите правильно примеры, и пропадут оставшиеся. Ну а кто успеет раньше остальных выполнить задание и решит пример: 272 000 : 800 (стр.
Проговаривается выполнение каждого примера. Дети проговаривают решение примера с опорой на эталон, составленный на уроке.
-
У кого были ошибки? Дети поднимают руки.
-
Какие ошибки вы допустили?
-
Кто ошибся в вычислениях?
-
Кто ошибся в алгоритме деления?
-
Что станет вашей целью в дальнейшем? (Научиться применять эталон деления круглых чисел, тренироваться в делении на однозначное «углом»)
-
Кто справился с заданием? О чём это говорит? (Мы поняли, как делить круглые числа )
-
Поставьте на бересте букву «Х», у кого есть ошибки -«?».
8. Включение в систему знаний и повторение.
Организация учебного процесса на этапе 8:
– Где вам пригодятся новые знания? (При решении задач и уравнений).
-
Откройте стр.25 № 4. Прочитайте задание. (Составь уравнение и реши его.)
-
Вам нужно выполнить пока только первую часть задания: составить уравнения и подчеркнуть то, которое мы не сможем выполнить, пользуясь нашим новым алгоритмом.
У детей в тетрадях:
а) Х • 80 = 68 800 б) Х : 500 = 8 560 в) 720 630 : Х = 90
-
Проверьте запись. Учитель открывает запись, уравнение Х :500 = 8 560 не подчеркнуто.
-
Назовите, какое уравнение подчеркнули?
-
Из оставшихся выберите любое и решите его. 2 ученика работают у доски. Затем работа проверяется фронтально.
Поднимите руку те, кто заработал еще одну букву имени лучшего друга маленькой Бабы-Яги. Молодцы! Записывайте: буква «А».
-
Маленькая Баба-Яга как и многие дети любит решать задачки, но не любит их долго записывать.
Много задач, но мало записи… Мы работаем с …(«Блиц – турниром») на с.26, № 7.
-
Ваша задача не трудная, но надо быть очень внимательными. Выберите из нескольких выражений только то, что является выражением к задаче, и запишите его в рамке. Учитель может записать выражения на доске, а может повесить Д-16.
а) а : 3 • 7 а : 7 • 3 3 • а • 7
б) (b : 2) : c c : (b : 2) (b : 2) • c c : 2 • b
в) n : 4 + n n + n : 4 n + n • 4
г) c + d :2 c – d :2 (c + d) : 2 (c – d) : 2 + d
д) (x – y) : 2 x – y (x + y) : 2 – y (x – y) : 2 — y
-
Проверим.
Один ученик выходит к доске, снимает (стирает) лишние выражения, объясняет задачу по выбранному им выражению.
9. Рефлексия учебной деятельности на уроке.
Организация учебного процесса на этапе 9:
-
Какую цель ставили перед собой? (Создать алгоритм и эталон деления круглых чисел и научиться решать примеры с применением этого эталона)
-
Достигли ли вы цели? Как доказать? (Создали эталон и добавили в алгоритм дополнительный шаг, на основе которых можно решать примеры на деление круглых чисел).
-
Как достигали цели? (Мы составили план работы и действовали по плану.)
-
На что опирались при составили плана? (На известные нам «эталон деления на 10, 100, 1000» и на алгоритм деления многозначного числа на однозначное в столбик.)
-
Докажите, что вы сегодня были настоящими учениками.
Перечислите шаги учебной деятельности. (Мы сначала узнали, что не знаем и сами нашли способ).
-
Где вам может пригодиться новое знание? (При решении примеров, задач и уравнений.)
-
Да, вы теперь больше знаете и стали сильнее в своих знаниях. Оцените свою работу, если вы чувствуете прибавление сил и довольны своей работой, повести рядом с Маленькой Бабой-Ягой изображение ее друга ворона Абрахаса, если вас что-то не устаивает, вы не очень довольны своей работой прикрепите бересту, на которой писали имя.
-
Много теперь друзей у маленькой Бабы-Яги. Но есть и береста, посоветуйте друг другу, что надо ребятам делать? (Не надо расстраиваться, надо тренироваться решать примеры, задачи и уравнения.)
-
Вы правы, у маленькой Бабы-Яки то же не все получалось сразу, не зря она дошла только до 230 страницы колдовской книги.
-
Вы хотите потренироваться, что бы закрепить свои силы?
-
Домашнее задание:
повторить прием деления круглых чисел по эталону и алгоритма, проговорить их вслух дома при выполнении вычислений;
стр.
25 № 4 (нерешенное уравнение по нашей теме), стр. 26 № 6
☺ стр. 26 №10, №11(по желанию)
Когда вы это сможем сделать? (Дома и на следующем уроке.)
6
Закрепление умений выполнять деление с остатком
Конспект урока математики на тему :
«Закрепление умений выполнять деление с остатком».
3 класс.
Автор УМК: М. И. Моро (УМК «Школа России»).
Цели: закрепление умений выполнять деление с остатком; закрепление умений выполнять внетабличное умножение и деление.
Планируемые результаты
Предметные:
закрепление умений выполнять деление с остатком;
закрепление умения выполнять внетабличное умножение и деление.
закрепление умения решать задачи
Метапредметные:
Познавательные
— Учить самостоятельно выделять и формулировать познавательную цель.
— Выделять необходимую информацию, при работе с учебником.
-уметь применять правила и пользоваться алгоритмом.
Личностные
— Развитие познавательных интересов, учебных мотивов.
— Уметь оценивать свою работу и работу одноклассников.
Регулятивные
— Контроль способа выполнения действия.
— Внесение необходимых дополнений и коррективов в план выполнения действия (в случае необходимости).
— Выделение и осознание того, что уже усвоено и что еще нужно усвоить.
Коммуникативные
— Планирование, сотрудничество с учителем и сверстниками.
— Умение в рамках совместной учебной деятельности слушать других.
осуществлять контроль и результат деятельности,
Технологии используемые на уроке:
-ИКТ технологии;
-технология смыслового чтения;
-здоровье сберегающая технология.
Оборудование:
учебник «Математика», раб тетрадь 3 класс, Моро М.И., Бантова М.А.,
презентация к уроку, компьютер, мультимедийная установка
карточки с тестом, алгоритм деления с остатком.
Ход урока
- Организационный момент
2.Актуализация знаний.
— Ребята, с какой темой мы познакомились на прошлом уроке? (Деление с остатком.)
— Сегодня мы с вами продолжим работать над этой темой и откроем много нового.
Устный счёт
-Поспорь с Незнайкой, который рассказал о себе следующее: (2 слайд)
«Я хорошо знаю математику! Я выучил таблицу умножения, умею складывать, вычитать и делить.
Я знаю, что самое большое двузначное число 100 можно разделить без остатка на 2, 3, 4 и 5.»
-Найдите ошибки в его фразах -на интерактивной доске ученик подчёркивает ошибки.
-Помогите Незнайке решить задачи: (3 слайд)
1.
Сколько птиц? Ответь скорей.
2. На дорожке сидели 6 воробьев, к ним прилетели еще 5 воробьев, а
потом еще 11. Кот подкрался и
схватил 1 воробья.
Сколько воробьев осталось на дорожке?
(4 слайд) -Незнайка просит вас назвать числа,
которые без остатка делятся
а) на 5: 25, 29, 30, 37, 40, 46, 50,
б) на 7: 9, 14, 20, 21, 28, 35, 43, 49;
в) на 4: 12, 14, 16, 20, 24, 34, 39, 40.
(5 слайд) Зашифрованное слово.
— Угадайте зашифрованное слово.
| У | 28:3 | Г | 24:6 | И | 24:3 | ||
| А | 15:5 | Ш | 18:4 | Т | 49:7 | ||
| Т | 34:6 | О | 81:9 | Я | 12:5 | ||
| Л | 21:7 | Р | 35:5 | М | 45:9 |
-Надо решить только выражения, которые без остатка делятся.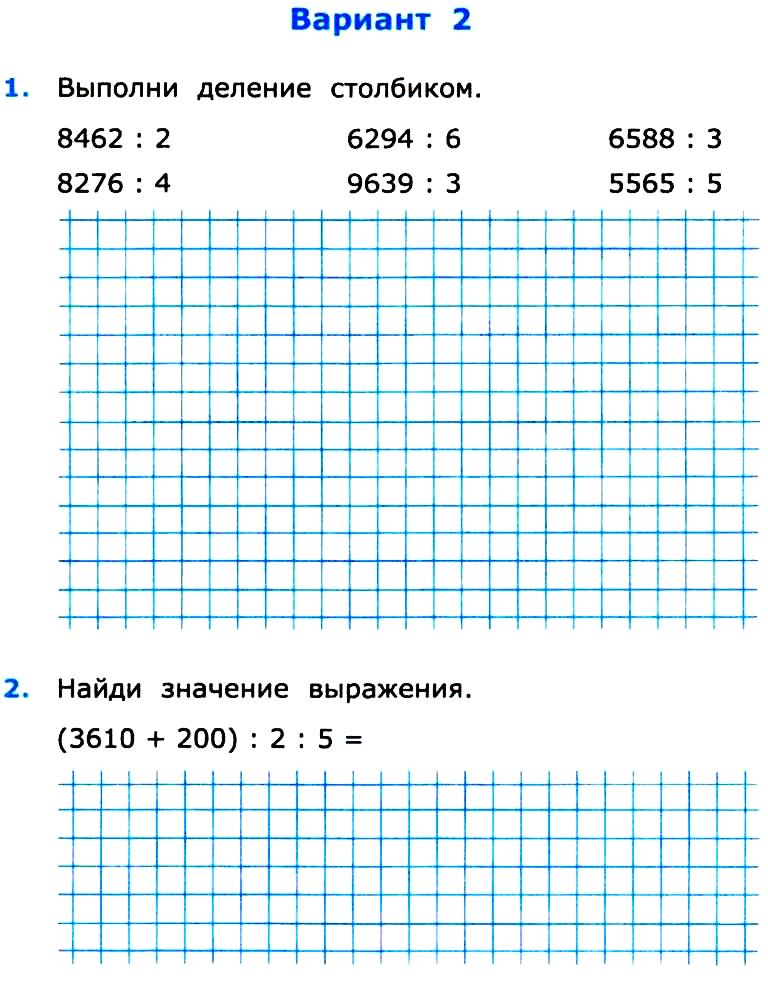
-Получилось слово- алгоритм. Давайте вспомним алгоритм деления с остатком. Расположите карточки по порядку:
- Находим наибольшее число, которое можно разделить на делитель без остатка.
- Данное число делим на делитель. Это значение частного.
- Вычитаем разделившееся число из делителя – это остаток.
- Проверяем, остаток должен быть меньше делителя.
3.Закрепление умений выполнять деление с остатком
— Откройте свои тетради. Запишите число, классная работа. Не забывайте, что в тетрадях нужно писать красиво и аккуратно. Тетради положите правильно, спинки прямые.
— Откройте учебники на с 28, выполним задание №1.
-Решим примеры столбиком, используя алгоритм деления с остатком
Какое правило знаем при делении с остатком? (При делении остаток всегда должен быть меньше делителя.)
( Учащиеся выполняют задание на доске и в терадях)
Физкультминутка (6 слайд)
Решение задачи № 3
— Прочитайте задачу.
— Как удобнее оформить краткую запись? (С помощью таблицы.)
— Что обозначают числа 54, 90, 72? (Общее число листов.)
— Что обозначает число 3? (Количество тетрадей.)
— Что надо узнать в задаче? (Сколько таких тетрадей получится из 90 листов, из 72 листов.)
— Что сказано о количестве листов в 1 тетради? (Одинаковое.)
1ученик работает за доской, затем объясняет решение задачи.
1). 54:3=18(л.)- в одной тетради.
2). 90:18= 5(т.)- получится из 90 листов.
3) 72:18=4(т.)
Ответ: 5 тетрадей получится из 90 листов бумаги, 4 тетради из 72 листов.
5.Самостоятельная работа с последующей проверкой
6.Рефлексия(8 слайд)
— Понравилось ли вам на уроке?
— Что показалось самым интересным на уроке?
— С каким правилом познакомились на уроке? (При делении остаток всегда должен быть меньше делителя.)
- Было трудно …
- Было интересно
— Молодцы, ребята! Закрываем тетради, урок окончен!
— Спасибо за урок!
7.
примеры с решениями и объяснением. Примеры на деление для самопроверки
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Как объяснить ребенку деление двузначного числа на однозначное не в столбик?
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя.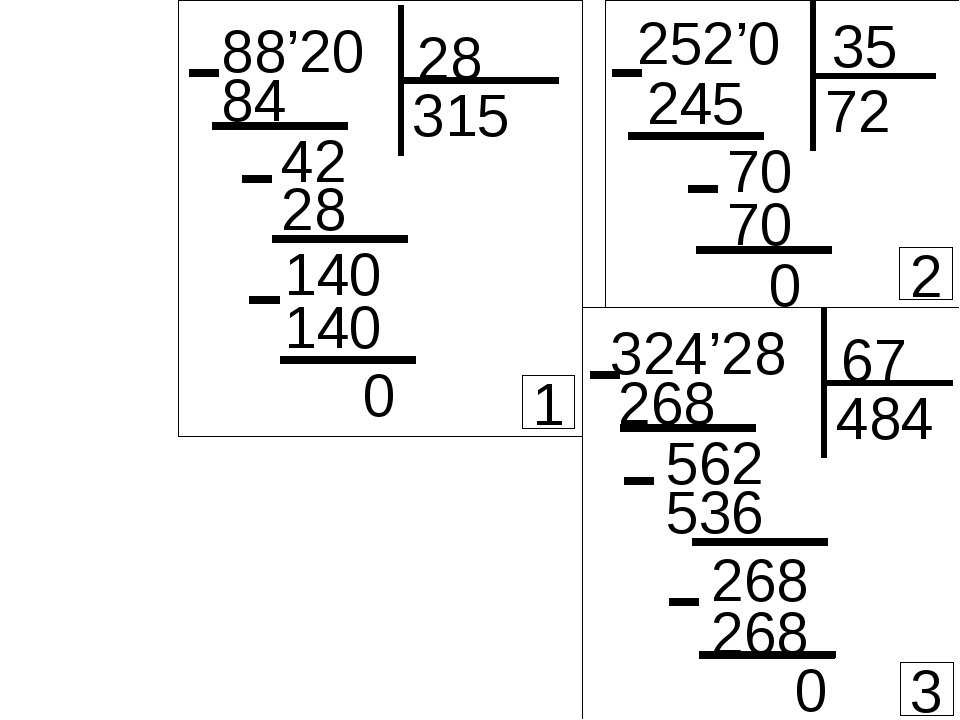
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96.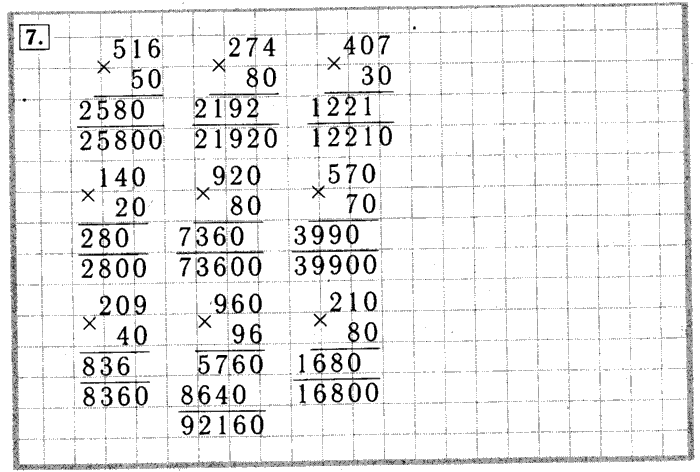
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение .(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
Деление в игровой форме
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой форме
Таким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбик
Прежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
- Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.
Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза.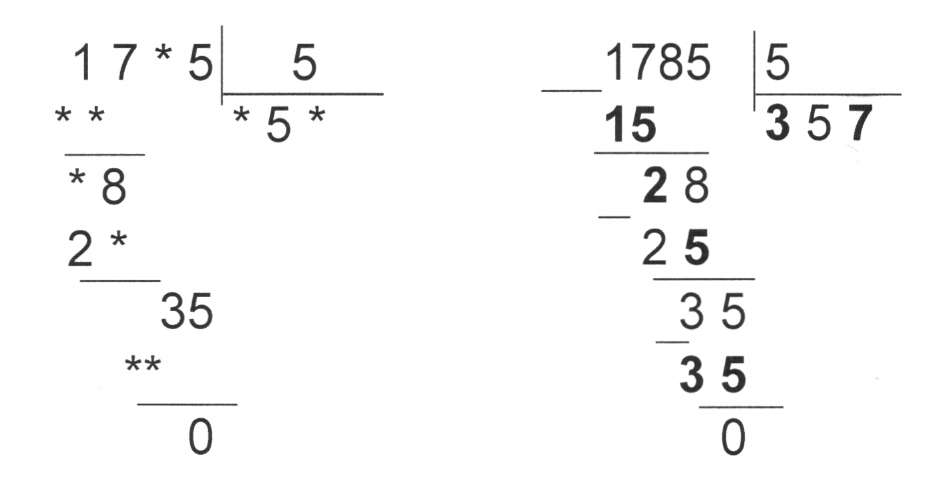
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению.
За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление столбиком (также можно встретить название деление уголком) — стандартная процедура в
арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания
деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел
с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при
делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком
удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными
числами изображается символ вида
.
Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в
столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного,
остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет
записано ниже делителя под горизонтальной чертой.
делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
512:8=?
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого.
Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать
с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую
слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми
цифрами.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит.
это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая
таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48
→ записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над
самой правой цифрой
произведения .
4. Между 51 и 48 слева поставим «-» (минус).
Вычтем по
правилам вычитания в столбик 48 и под чертой
запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в
этом пункте не является самым последним действием, полностью завершающим процесс деления
столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение
более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не
стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в
записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего
вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в
скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично.
«промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.
- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном
записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить
поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число
получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего,
меньшего разряда и продолжать деление.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10.
Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения.
В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
html — 8 столбцов в Twitter Bootstrap
Я знаю, что это довольно старая тема, но это лучший результат поиска по этой проблеме, поэтому я надеюсь, что все в порядке, что я получил ответ, который, на мой взгляд, лучше, чем любой из текущих вариантов, представленных здесь.
В макете из n столбцов я не хочу перебирать какие-то странные вещи .row .col- , которые не позволяют мне изменять размер при перемещении вниз в точках останова.
Например, текущий принятый ответ здесь правильно указывает, что вы не можете сделать это с помощью начальной загрузки по умолчанию, но следующий ответ в строке предполагает, что вы вкладываете .col-xs-3 внутри .col-xs-6 , и я предполагаю, что многие люди, приходящие сюда, используют это, потому что это единственный работоспособный ответ, который вы можете найти на первой странице поиска Google .
Что делать, если мне нужно 8 столбцов на точке останова lg , а затем 4 столбца на планшетах и 2 столбца на мобильном устройстве? Этот ответ не ухудшается изящно. Этот метод будет, и его невероятно легко реализовать.
Сначала добавьте это в свой файл CSS:
.col-xs-8r,
.кол-см-8р,
.col-md-8r,
.col-lg-8r {
положение: относительное;
мин-высота: 1px;
отступ справа: 15 пикселей;
отступ слева: 15 пикселей;
}
.col-xs-8r {
ширина: 12,5%;
плыть налево;
}
@media (min-width: 768 пикселей) {
.col-sm-8r {
ширина: 12,5%;
плыть налево;
}
}
@media (min-width: 992px) {
.col-md-8r {
ширина: 12,5%;
плыть налево;
}
}
@media (min-width: 1200 пикселей) {
.col-lg-8r {
ширина: 12,5%;
плыть налево;
}
}
Затем добавьте col - * - 8r в свои столбцы, например:
Теперь у вас есть макет из 8 столбцов, который может работать на всех точках останова.
Самое замечательное в этом методе заключается в том, что если вам нужно нечетное количество столбцов, его очень легко расширить. Вы просто делите 100 на необходимое количество столбцов, а затем используете это число вместо 4 экземпляров ширины : 12,5%; в приведенном выше коде (очевидно, не забудьте обновить имена классов до любого числа, которое вы используете).
Например, если вам нужен макет из 7 столбцов, вы должны использовать абсурдно длинную ширину : 14.28571428571429% вместо этих 4 экземпляров измените имена классов на .col - * - 7r , а затем вы можете поместить имя класса в любое место.
html — Как разделить список в одной ul на 3 столбца
CSS3 flexbox тоже может:
ul {
flex-direction: столбец;
flex-wrap: обертка;
дисплей: гибкий;
высота: 100вх;
}
ul li {
гибкость: 1 0 25%;
}
Выше css создаст следующий макет:
+ -------------------- +
| 01 | 05 | 09 |
+ -------------------- +
+ -------------------- +
| 02 | 06 | 10 |
+ -------------------- +
+ -------------------- +
| 03 | 07 | 11 |
+ -------------------- +
+ -------------------- +
| 04 | 08 | 12 |
+ -------------------- +
* {box-sizing: border-box;}
тело {
маржа: 0;
}
.список {
flex-direction: столбец;
стиль списка: нет;
flex-wrap: обертка;
высота: 100вх;
дисплей: гибкий;
отступ: 0;
маржа: 0;
}
.list li {
нижняя граница: сплошной 1px #fff;
граница справа: сплошной 1px #fff;
гибкость: 1 0 25%;
отступ: 10 пикселей;
цвет: #fff;
}
.col1 {
фон: синий;
}
.col2 {
фон: оранжевый;
}
.col3 {
фон: зеленый;
} - Тест 1
- Тест 2
- Тест 3
- Тест 4
- Тест 5
- Тест 6
- Тест 7
- Тест 8
- Тест 9
- Тест 10
- Тест 11
- Тест 12
Если вам нужен следующий макет:
+ ----------------------- +
| 1 | 2 | 3 | 4 |
+ ----------------------- +
+ ----------------------- +
| 5 | 6 | 7 | 8 |
+ ----------------------- +
+ ----------------------- +
| 9 | 10 | 11 | 12 |
+ ----------------------- +
, вы можете использовать следующий css:
ul {
flex-wrap: обертка;
дисплей: гибкий;
}
ul li {
гибкость: 1 0 25%;
}
* {box-sizing: border-box;}
тело {
маржа: 0;
}
.список {
стиль списка: нет;
flex-wrap: обертка;
дисплей: гибкий;
отступ: 0;
маржа: 0;
}
.list li {
нижняя граница: сплошной 1px #fff;
гибкость: 1 0 25%;
отступ: 10 пикселей;
цвет: #fff;
}
.list li: nth-child (4n + 1) {
фон: синий;
}
.list li: nth-child (4n + 2) {
фон: оранжевый;
}
.list li: nth-child (4n + 3) {
фон: зеленый;
}
.list li: nth-child (4n + 4) {
фон: фиолетовый;
} - Тест 1
- Тест 2
- Тест 3
- Тест 4
- Тест 5
- Тест 6
- Тест 7
- Тест 8
- Тест 9
- Тест 10
- Тест 11
- Тест 12
Синтетическое деление многочленов
Синтетическое деление многочленов
Чтобы разделить многочлены с помощью синтетического деления, необходимо выполнить деление линейным выражением, а ведущий коэффициент (первое число) должен быть равен 1.Например, вы можете использовать синтетическое деление для деления на x + 3 или x — 6, но вы не можете использовать синтетическое деление для деления на x 2 + 2 или 3x 2 — x + 7. Если ведущий коэффициент не равен 1, то вы должны разделить на ведущий коэффициент, чтобы превратить ведущий коэффициент в 1. Например, 3x — 1 станет
и 2x + 7 станет.
Если синтетическое деление не работает, вы должны использовать деление в столбик.
Вот шаги, необходимые для синтетического деления многочлена:
| Шаг 1 : | Для постановки задачи сначала установите знаменатель равным нулю, чтобы найти число, которое нужно поместить в поле деления.Затем убедитесь, что числитель записан в порядке убывания, и если какие-либо термины отсутствуют, вы должны использовать ноль для заполнения отсутствующего члена, наконец, перечислите только коэффициент в задаче деления. |
| Шаг 2 : | После правильной постановки задачи перенесите старший коэффициент (первое число) прямо вниз. |
| Шаг 3 : | Умножьте число в поле деления на число, которое вы выполнили, и поместите результат в следующий столбец. |
| Шаг 4 : | Сложите два числа и запишите результат внизу строки. |
| Шаг 5 : | Повторяйте шаги 3 и 4, пока не решите проблему. |
| Шаг 6 : | Напишите окончательный ответ. Окончательный ответ состоит из чисел в нижнем ряду, причем последнее число является остатком, а остаток должен быть записан в виде дроби.Переменные или x начинаются на одну степень меньше исходного знаменателя и уменьшаются на единицу с каждым членом. |
Пример 1 — Разделить:
Пример 2 — Разделить:
Щелкните здесь для практических задач
Пример 3 — Разделить:
Щелкните здесь для практических задач
Пример 4 — Разделить:
Щелкните здесь для практических задач
Пример 5 — Разделить:
Щелкните здесь для практических задач
Таблица распределения частот
: примеры, как сделать один
Содержание (щелкните, чтобы перейти к этому разделу):
См. Также: Таблица распределения частот в Excel
Частота сообщает вам , как часто что-то происходило .Частота наблюдения говорит вам, сколько раз наблюдение встречается в данных. Например, в следующем списке чисел частота числа 9 равна 5 (потому что оно встречается 5 раз):
1, 2, 3, 4, 6, 9, 9, 8, 5, 1, 1, 9, 9, 0, 6, 9.
Таблицы могут отображать либо категориальные переменные (иногда называемые качественными переменными), либо количественные переменные (иногда называемые числовыми переменными). Вы можете рассматривать категориальные переменные как категории (например, цвет глаз или марку корма для собак), а количественные переменные как числа.
Если вы не совсем уверены в разнице, см. Качественный или количественный? Как сказать.
В следующей таблице показано, какие методы планирования семьи использовали подростки в Квененге, Западная Ботсвана. В левом столбце показана категориальная переменная (Метод), а в правом столбце — частота — количество подростков, использующих этот конкретный метод (изображение любезно предоставлено KSU).
Таблица распределения частот, показывающая категориальные переменные.
Таблицы распределения частот
предоставляют вам снимок данных, чтобы вы могли найти закономерности.Беглый взгляд на приведенную выше таблицу частотного распределения показывает, что большинство подростков вообще не используют противозачаточные средства.
В начало
Пример 1
Счетные метки часто используются для составления таблицы распределения частот. Например, предположим, что вы обследуете несколько домашних хозяйств и выясняете, сколько у них домашних животных. Результаты: 3, 0, 1, 4, 4, 1, 2, 0, 2, 2, 0, 2, 0, 1, 3, 1, 2, 1, 1, 3. Глядя на эту цепочку чисел, вы непонятно. глаз; таблица частотного распределения упростит понимание данных.
Шаги
Чтобы составить таблицу частотного распределения, сначала впишите в один столбец категории (количество домашних животных):
Затем подсчитывают числа в каждой категории (из результатов выше). Например, число ноль появляется в списке четыре раза, поэтому поставьте четыре метки счета «||||»:
Наконец, подсчитайте метки и запишите частоту в последний столбец. Частота — это всего лишь сумма. У вас есть четыре счетных метки для «0», поэтому поставьте 4 в последний столбец:
К началу
Пример 2
Посмотрите видео или прочтите следующие шаги:
Как нарисовать таблицу распределения частот (немного более сложный пример)
Таблица распределения частот — это один из способов упорядочить данные, чтобы они имели больше смысла.Например, предположим, что у вас есть список показателей IQ для одаренного класса в конкретной начальной школе. баллов IQ : 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154. Этот список мало что говорит вам о что-нибудь. Вы можете нарисовать таблицу распределения частот , которая даст лучшее представление о ваших данных, чем простой список.
Как нарисовать таблицу распределения частот: шаги.
нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Часть 1: Выбор классов
Шаг 1: Определите, сколько классов (категорий) вам нужно.Нет никаких жестких правил о том, сколько классов выбрать, но есть несколько общих рекомендаций:
- Выберите от 5 до 20 классов. Для приведенного выше списка IQ мы выбрали 5 классов.
- Убедитесь, что у вас есть несколько предметов в каждой категории. Например, если у вас 20 предметов, выберите 5 классов (4 предмета на категорию), а не 20 классов (что даст вам только 1 предмет на категорию).
Примечание : Существует более математический способ выбора классов. Формула: журнал (наблюдения) журнал (2).Вы должны округлить ответ до следующего целого числа. Например, log17 log2 = 4.1 будет округлено до 5. (Спасибо Айману Масри за этот совет).
Часть 2: Сортировка данных
Шаг 2: Вычтите минимальное значение данных из максимального значения данных. Например, наш список IQ выше имел минимальное значение 118 и максимальное значение 154, поэтому:
154 — 118 = 36
Шаг 3: Разделите свой ответ на Шаге 2 на количество классов, которые вы выбрали на Шаге 1.
36/5 = 7,2
Шаг 4: Округлите число из шага 3 до целого числа, чтобы получить ширину класса. Округляя вверх, 7,2 получается 8 .
Шаг 5: Запишите наименьшее значение для первого минимального значения данных:
Наименьшее значение — 118
Шаг 6: Добавьте ширину класса из шага 4 к шагу 5, чтобы получить следующий нижний предел класса:
118 + 8 = 126
Шаг 7: Повторите шаг 6 для других минимальных значений данных (другими словами, продолжайте добавлять ширину вашего класса к минимальным значениям данных), пока вы не создадите количество классов, которое вы выбрали на шаге 1.Мы выбрали 5 классов, поэтому наши 5 минимальных значений данных:
118
126 (118 + 
134 (126 + 
142 (134 + 
150 (142 + 
Шаг 8: Запишите пределы верхнего класса. Это самые высокие значения, которые могут быть в категории, поэтому в большинстве случаев вы можете вычесть 1 из ширины класса и добавить его к минимальному значению данных. Например:
118 + (8-1) = 125
118-125
126-133
134-141
142-149
150-157
3.Завершение стола
Шаг 9: Добавьте второй столбец для количества элементов в каждом классе и пометьте столбцы соответствующими заголовками:
| IQ | Число |
|---|---|
| 118-125 | |
| 126-133 | |
| 134-141 | |
| 142-149 | |
| 150-157 |
Шаг 10: Подсчитайте количество предметов в каждом классе и поместите общее количество во второй столбец.Список значений IQ: 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154.
| IQ | Число |
|---|---|
| 118-125 | 4 |
| 126-133 | 6 |
| 134-141 | 3 |
| 142-149 | 2 |
| 150-157 | 2 |
Вот как легко составить таблицу распределения частот!
Понравилось объяснение? Ознакомьтесь с нашей статистикой с практическими рекомендациями, с сотнями других пошаговых решений, таких как это!
Совет . Если вы работаете с большими числами (например, сотнями или тысячами), округлите шаг 4 до большого целого числа, которое легко преобразовать в классы, например 100, 1000 или 10 000.То же самое и с очень маленькими числами — вы можете округлить до 0,1, 0,001 или аналогичного деления.
В начало
Список литературы
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Операторы деления в Python — GeeksforGeeks
Операторы деления в Python
Рассмотрим приведенные ниже инструкции в Python.
Python3
печать ( 5 / / 2 )
/ 0005 ( 0005 - 0005) 2 )
Выход:
2 -3
Первый вывод хорош, но второй может удивить, если мы придем в мир Java / C ++.В Python оператор «//» работает как разделение полов для целочисленных аргументов и аргументов с плавающей запятой. Однако оператор / возвращает значение с плавающей запятой, если одним из аргументов является число с плавающей запятой (аналогично C ++)
Примечание:
Оператор «//» используется для возврата ближайшего целочисленного значения, которое меньше, чем или равно указанному выражению или значению. Итак, из приведенного выше кода 5 // 2 возвращает 2. Вы знаете, что 5/2 равно 2,5, ближайшее целое число, которое меньше или равно 2 [5 // 2]. (Это обратное к обычным математическим вычислениям в по обычной математике значение 3).
Python3
печать ( 5,0 / 2 )
печать - )
Выход:
2,5 -2,5
Реальный оператор деления этажа — «//». Он возвращает минимальное значение как для целочисленных, так и для аргументов с плавающей запятой.
Python3
печать ( 5 / / 2 )
/ - 2 )
печать ( 5,0 / / 2 )
печать ( - -0 / / 2 )
Выход:
2 -3 2.0 -3.0
См. Это для примера.
Автор статьи: Arpit Agrawal . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединяйтесь к Машинное обучение — курс базового уровня
| College Algebra Урок 37: Synthetic Division and Теоремы об остатке и множителе Цели обучения После изучения этого руководства вы сможете:
Введение В этом уроке мы рассмотрим синтетическое деление. Учебник Синтетическое деление — это еще один способ разделить полином на бином x — c , где c равно Шаг 1: Установите синтетический Самый простой способ сделать это — сначала настроить его, как если бы вы долго Если вам нужен обзор постановки задачи деления в столбик, не стесняйтесь Делитель (то, на что вы делите) находится снаружи коробки. Когда вы выписываете дивиденд, убедитесь, что вы записываете его в порядке убывания . Это позволит вам выстраивать термины, когда вы решите проблему. Когда вы настраиваете это с помощью синтетического деления, напишите c для делителя x — c . Шаг 2: Вниз Шаг 3: Умножьте c на значение, только что записанное в нижней строке. Поместите это значение сразу под следующим коэффициентом в дивиденде: Шаг 4: Добавьте Запишите сумму в нижней строке: Шаг 5: Повторить Шаг 6: Запишите Числа в последней строке составляют ваши коэффициенты частного Степень частного на единицу меньше степени дивиденда. Пример Синтетическое подразделение будет выглядеть так:
Числа в последней строке составляют ваши коэффициенты частного Пример Синтетическое подразделение будет выглядеть так:
Числа в последней строке составляют ваши коэффициенты частного Теорема об остатке Если полином f ( x ) делится на x — c , затем Это означает, что мы можем применить синтетическое деление и последнее число Пример Используя синтетическое деление, чтобы найти остаток, мы получаем: Опять же, на этот раз наш ответ — не частное, а остаток. Окончательный ответ: f (-2) = -27 Теорема о множителях Если f ( x ) является полиномом И 1) f ( c ) = 0, тогда x — c является множителем f ( x ). 2) x — c — коэффициент f ( x ), Имейте в виду, что алгоритм деления делимое = делитель (частное) + напоминание Итак, если напоминание равно нулю, вы можете использовать это, чтобы помочь вам разложить многочлен на множители. Вы можете использовать синтетическое разделение, чтобы помочь вам с этим типом проблемы. Пример Используя синтетическое деление, чтобы найти частное, мы получаем: Обратите внимание, что остаток равен 0. Это означает, что ( x — 2) является множителем. Перезапись f ( x ) Нам нужно закончить эту проблему, установив это равным нулю и
Нули этой функции равны x = 2, Пример Используя синтетическое деление, чтобы найти частное, мы получаем: Обратите внимание, что остаток равен 0. Это означает, что ( x — 3/2) является множителем. Перезапись f ( x ) Нам нужно закончить эту проблему, установив это равным нулю и
Решение или нули этой функции: x = 3/2, -1 и 1. Практические задачи Это практические задачи, которые помогут вам перейти на следующий уровень. Чтобы получить максимальную отдачу от них, вы должны решить проблему
Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 15 марта 2012 г. |
Статистика: сила из данных! Организация данных: Таблицы частотного распределения
Архивный контент
Информация, помеченная как архивная, предназначена для справки, исследования или ведения записей. Он не регулируется веб-стандартами правительства Канады и не изменялся и не обновлялся с момента его архивирования.Свяжитесь с нами, чтобы запросить формат, отличный от доступных.
Частота ( f ) конкретного наблюдения — это количество раз, когда наблюдение встречается в данных. Распределение переменной — это образец частот наблюдения. Частотные распределения представлены в виде таблиц частот, гистограмм или многоугольников.
Частотные распределения могут показывать либо фактическое количество наблюдений, попадающих в каждый диапазон, либо процент наблюдений.В последнем случае распределение называется распределением относительной частоты .
Таблицы частотного распределения могут использоваться как для категориальных, так и для числовых переменных. Непрерывные переменные следует использовать только с интервалами классов, которые будут вскоре объяснены.
Обследование было проведено на Мейпл-авеню. В каждом из 20 домов людей спрашивали, сколько автомобилей зарегистрировано в их домохозяйствах. Результаты были записаны следующим образом:
1, 2, 1, 0, 3, 4, 0, 1, 1, 1, 2, 2, 3, 2, 3, 2, 1, 4, 0, 0
Используйте следующие шаги, чтобы представить эти данные в таблице частотного распределения.
- Разделите результаты ( x ) на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае интервалами будут количество домашних хозяйств без машины (0), одна машина (1), две машины (2) и так далее.
- Составьте таблицу с отдельными столбцами для номеров интервалов (количество автомобилей в семье), суммированных результатов и частоты результатов в каждом интервале. Обозначьте эти столбцы Количество автомобилей , Tally и Частота .
- Прочтите список данных слева направо и поместите отметку в соответствующей строке. Например, первым результатом будет 1, поэтому поместите отметку в строке рядом с местом, где в столбце интервала стоит 1 ( Количество автомобилей ). Следующим результатом будет 2, поэтому поместите отметку в строке рядом с 2 и так далее. Когда вы достигнете пятой отметки, проведите линию подсчета через предыдущие четыре отметки, чтобы облегчить чтение окончательных расчетов частоты.
- Сложите количество отметок в каждой строке и запишите их в последний столбец под названием Частота .
Ваша таблица распределения частот для этого упражнения должна выглядеть так:
Быстро посмотрев на эту таблицу частотного распределения, мы можем увидеть, что из 20 обследованных домашних хозяйств 4 домашних хозяйства не имели автомобилей, 6 домашних хозяйств имели 1 машину и т. Д.
Начало страницы
Кумулятивная таблица распределения частот — это более подробная таблица. Она выглядит почти так же, как таблица распределения частот, но в нее добавлены столбцы, в которых указывается совокупная частота и совокупный процент результатов.
На недавнем шахматном турнире все 10 участников должны были заполнить форму, в которой были указаны их имена, адрес и возраст. Возраст участников был записан следующим образом:
36, 48, 54, 92, 57, 63, 66, 76, 66, 80
Используйте следующие шаги, чтобы представить эти данные в таблице совокупного распределения частот.
- Разделите результаты на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае уместны интервалы в 10 раз.Поскольку 36 — самый низкий возраст, а 92 — самый высокий, начинайте интервалы с 35 до 44 и заканчивайте интервалы с 85 до 94.
- Создайте таблицу, аналогичную таблице частотного распределения, но с тремя дополнительными столбцами.
Кумулятивная таблица распределения частот должна выглядеть следующим образом:
Таблица 2. Возраст участников шахматного турнира 35 44 1 1 10.0 10,0 45 54 2 3 20,0 30,0 55 64 2 5 20,0 50,0 65 74 2 7 20,0 70,0 75 84 2 9 20.0 90,0 85 94 1 10 10,0 100,0
Для получения дополнительной информации о том, как создавать таблицы накопленной частоты, см. Раздел «Совокупная частота» и «Совокупный процент».
Начало страницы
Классные перерывы
Если переменная принимает большое количество значений, то проще представить и обработать данные, сгруппировав значения в интервалы классов.Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
Для иллюстрации предположим, что мы установили возрастные диапазоны для исследования молодых людей, учитывая при этом возможность того, что некоторые пожилые люди также могут попасть в сферу нашего исследования.
Частота интервала классов — это количество наблюдений, которые происходят в конкретном предопределенном интервале. Так, например, если в данных нашего исследования фигурирует 20 человек в возрасте от 5 до 9 лет, частота для интервала 5–9 составляет 20.
Конечные точки интервала класса — это наименьшее и наибольшее значения, которые может принимать переменная. Итак, интервалы в нашем исследовании составляют от 0 до 4 лет, от 5 до 9 лет, от 10 до 14 лет, от 15 до 19 лет, от 20 до 24 лет и от 25 лет и старше. Конечные точки первого интервала — 0 и 4, если переменная дискретная, и 0 и 4,999, если переменная непрерывная. Конечные точки других интервалов классов будут определены таким же образом.
Ширина интервала класса — это разница между нижней конечной точкой интервала и нижней конечной точкой следующего интервала.Таким образом, если непрерывные интервалы нашего исследования составляют от 0 до 4, от 5 до 9 и т. Д., Ширина первых пяти интервалов равна 5, а последний интервал является открытым, поскольку ему не назначена более высокая конечная точка. Интервалы также могут быть записаны как от 0 до менее 5, от 5 до менее 10, от 10 до менее 15, от 15 до менее 20, от 20 до менее 25 и 25 и более.
Правила для наборов данных, содержащих большое количество наблюдений
Таким образом, следуйте этим основным правилам при построении таблицы частотного распределения для набора данных, который содержит большое количество наблюдений:
- найти наименьшее и наибольшее значения переменных
- определиться с шириной классных интервалов
- включают все возможные значения переменной.
При выборе ширины интервалов между классами вам нужно будет найти компромисс между достаточно короткими интервалами, чтобы не все наблюдения попадали в один интервал, но достаточно длинными, чтобы в итоге вы не получили только один наблюдение за интервал.
Также важно убедиться, что интервалы классов являются взаимоисключающими.
Начало страницы
Было протестировано тридцать батареек AA, чтобы определить, на сколько их хватит.Результаты с точностью до минуты были записаны следующим образом:
423, 369, 387, 411, 393, 394, 371, 377, 389, 409, 392, 408, 431, 401, 363, 391, 405, 382, 400, 381, 399, 415, 428, 422, 396 , 372, 410, 419, 386, 390
Используйте шаги из примера 1 и приведенные выше правила, чтобы помочь вам построить таблицу частотного распределения.
Ответ
Наименьшее значение — 363, максимальное — 431.
Используя заданные данные и интервал классов 10, интервал для первого класса составляет от 360 до 369 и включает 363 (наименьшее значение).Помните, что всегда должно быть достаточно интервалов между классами, чтобы было включено самое высокое значение.
Заполненная таблица распределения частот должна выглядеть так:
Начало страницы
Относительная частота и процентная частота
Аналитик, изучающий эти данные, может захотеть узнать не только, на сколько хватает батарей, но и какая доля батарей попадает в интервал срока службы батарей каждого класса.
Эта относительная частота определенного наблюдения или интервала классов находится путем деления частоты ( f ) на количество наблюдений ( n ): то есть ( f ÷ n ).Таким образом:
Относительная частота = частота ÷ количество наблюдений
Частота в процентах находится путем умножения каждого значения относительной частоты на 100. Таким образом:
Частота в процентах = относительная частота X 100 = f ÷ n X 100
Начало страницы
Используйте данные из Примера 3, чтобы составить таблицу с относительной частотой и процентной частотой каждого интервала срока службы батареи.
Вот как выглядит эта таблица:
| 360–369 | 2 | 0,07 | 7 |
|---|---|---|---|
| 370–379 | 3 | 0,10 | 10 |
| 380–389 | 5 | 0,17 | 17 |
| 390–399 | 7 | 0,23 | 23 |
| 400–409 | 5 | 0.17 | 17 |
| 410–419 | 4 | 0,13 | 13 |
| 420–429 | 3 | 0,10 | 10 |
| 430–439 | 1 | 0,03 | 3 |
| Всего | 30 | 1,00 | 100 |
Теперь аналитик этих данных может сказать, что:
- 7% батареек AA имеют срок службы от 360 минут до, но менее 370 минут, и это
- вероятность того, что срок службы любой случайно выбранной батареи AA будет в этом диапазоне, составляет приблизительно 0.
После введения в общеобразовательные учреждения новых образовательных стандартов, на каждой ступени обучения стало обязательным проведение исследований либо проектов. Не является исключением и такая учебная дисциплина как арифметика. Разнообразные математические проекты, сделанные в группах, отдельными учениками, способствует формированию познавательного интереса к предмету.
Проектная деятельность в начальной школе
В третьем классе ребята могут сочинять какие-то сказки, связанные с числами, элементарными действиями: вычитанием, сложением. Проектная деятельность, которая в настоящее время является обязательным элементом работы педагогов начальной школы, направлена на саморазвитие подрастающего поколения, стремление младших школьников к получению новых знаний, навыков.
Рассмотрим различные математические проекты, которые созданы ребятами под руководством своих наставников, а также с привлечением родителей.
Что потребуется для работы?
Используя современные информационные технологии, можно приступить к творчеству. Математические проекты, которые придумывают ребята начальной школы, могут стать настоящей детективной историей. Безусловно, помимо фантазии, проект предполагает наличие у школьников определенных умений и навыков, чтобы сказка или история не содержала вычислительных ошибок.
«Пропавшая цифра»
Предлагаем готовый математический проект. 3 класс – возраст, в котором ребята предпочитают активные игры, необычные истории. Рассказ о «пропавшей пятерке» по праву можно считать настоящим детективом.
Однажды Маша, ученица 3 класса, выполняла домашнее задание по математике. Как только она записала в свою тетрадь уравнение, раздался телефонный звонок. Маша вышла из-за стола, ушла в другую комнату. Если бы девочка увидела, что в этот момент происходило в ее тетрадке, она бы изрядно удивилась. Итак, пока хозяйка записей отсутствовала, произошло преступление. На место прибыл следователь Равно. Он увидел необычную запись: А-4=5.
-Странно, здесь стоит знак «минус», следовательно, произошла кража, — сделал предположение следователь Равно.
И вблизи места происшествия стояла Пятерка, которая громко плакала:
— Караул! Украли! У меня украли Четверку! Я только на минутку отвернулась, а ее уже нет.
— Успокойтесь, не волнуйтесь, пожалуйста, и попробуйте вспомнить, не обнаружили ли вы кого-то странного объекта неподалеку? — поинтересовался Равно.
— Я видела, как какой-то странный А в маске и темном пальто прятался за цветочными кустами.
— Данный мистер А, вероятнее всего, и есть неизвестный похититель. Необходимо его найти! — предположил Равно.
Следователь пришел в детективное бюро и начал просматривать фотографии различных преступников. Он даже вспомнил одно свое дело о том, что число «Одиннадцать» покушалось на здоровье господина Сто Два. В качестве отличительной приметы преступника тогда был именно темный плащ.
Следователь Равно воскликнул:
— Понятно, безусловно, я понял кто преступник! Срочно нужно его допросить!
И тогда Равно отправился в дом к Одиннадцати. Но ему удалось застать только его жену. Оказалось, что Одиннадцать находится в тюрьме за совершенное преступление. Это подтверждает его алиби, он не мог похитить Четыре у госпожи Пятерки.
Равно огорчился: его версия оказалась ошибочной. Он направился к выходу, но тут жена Одиннадцати вспомнила, что на днях к ней заходил господин Девятка, брал на время темный плащ.
— Огромное спасибо за такие важные сведения! — попрощался следователь Равно и отправился на поиски Девятки.
Он оказался дома, и Равно начал свой допрос.
— Ты украл у Пятерки Четверку? – строго спросил Равно.
Девятка ответил:
— Это точно не я! У меня темного плаща нет!
— Скажи, откуда ты знаешь, что на воре был темный плащ? А ну-ка, покажи, что у тебя в шкафу! – потребовал Равно.
Девятка открыл шкаф, и тут Равно увидел, что там висит плащ.
— Мы проведем следственный эксперимент, одевайся, — сказал Равно.
После того, как они оказались на месте преступления, Пятерка ждала их.
— Приступим к следственному эксперименту. Пятерка, возвращайтесь на то место, где у вас пропала Четверка. А ты, Девятка, иди на место А.
После того как Девятка зашла в уравнение, получилось выражение 9-4=5
— Пятерка, узнаете преступника? – спросил следователь Равно.
— Да! Безусловно! — закричала Пятерка.
Пришлось Девятке признаваться:
— Да, это я украл Четверку. Она находится в моем доме. Пожалуйста, простите меня, обещаю, не буду больше так себя вести.
После того. как Четверка была спасена, Пятерка стала самой счастливой цифрой на свете. Следователю Равно удалось раскрыть еще одно совершенное преступление.
Сказка из страны Цифрографии
Предлагаем еще один проект — «Математические сказки».
Жили — были числа в одной волшебной стране. И тут задумал Ноль уйти из королевства, отправиться в путешествие. Он хотел попасть в страну Букварию, чтобы узнать, чем занимаются ее жители. По пути Ноль встретил Единицу, она была выше Ноля, поэтому пошла впереди, у них получилась десятка. По дороге к ним примкнула пятерка, получилась число 105. переходя через мост, пятерка выскочила вперед, образовалось число 510.
Они подружились, и вместе отправились в страну Букварию. В этой стране они познакомились с интересными и загадочными буквами: А, И, Б. В результате их дружбы появились необычные сочетания, которые стали использовать любители шахматной игры.
«Работяга Нолик»
Рассмотрим его один проект про математические сказки. Его можно использовать на обобщающем занятии либо для внеклассного мероприятия.
Проект «Математические сказки про ноль и единицу» вызовут у ребят интерес. Решили Большие Числа расслабиться, направились они в ресторан. Среди них оказались: Колода, Ворон, Тьма, Биллион, Миллиард, Квинтильон, Квадрильон, Секстиллион.
Обедали они, как полагается, ухой с семгой, пирогами со стерлядью, перед ними выступали цыгане. А официантом работал Нолик. Он едва успевал бегать с кухни к столикам, подавая новые кушанья, убирая разбитое гостями стекло.
— Что крутишься под моими ногами? – закричал Ворон.
— Нет ему места среди таких господ, как мы, — промолвил Квадрильон, — пускай пойдет вон.
Колода дала бедному Нолику подзатыльник. Надоело ему терпеть унижения, он ушел. Что произошло со зваными господами? Без Нолика они стали обычными единицами, которые никому не были интересны. До сих пор они ищут Нолика, хотят перед ним извиниться. Прошло много времени, но они так и не смогли найти трудолюбивого Нолика, который впервые в жизни почувствовал себя абсолютно свободным и счастливым числом.
Важная дробь
Необычные математические проекты, создаваемые ребятами в начальной школе, помогают им осознать важность и значимость «царицы наук». В качестве помощников при придумывании творческой работы, могут выступать родители.
Проект по математике «Математические загадки» можно сделать в виде сказки.
На белом свете жила Дробь, у которой было два верных друга: Знаменатель и Числитель. Дробь считала, что она самая важная, а потому пыталась унижать Знаменатель. Чем сильнее она его обижала, тем меньше он становился, а сама Дробь раздувалась от важности.
Наступил такой момент, когда Знаменатель превратился в ноль, и тогда Дробь лопнула от злости.
Сказка о Единице
Как правильно сделать проект по математике — 3 класс? Математические сказки можно сочинить, используя элементарные вычислительные навыки. Например, в ней могут участвовать в качестве главных героев цифры. Как можно оформить математический проект? 3 класс – этот тот возраст, когда ребята с удовольствием рисуют, лепят, создают аппликации из цветной бумаги. Например, сказочный проект о Единице можно создать, вооружившись цветной бумагой, творческим воображением. Единицу ребята могут представить в виде красивой девочки. Что еще можно включить в этот проект по математике? 3 класс — математические навыки у ребят уже достаточно сформированы, поэтому девочка Единица может совершать покупки, которые также будут присутствовать в аппликации.
Интересная история
Предлагаем еще один проект по математике. Математические сказки можно сочинять, пользуясь произведениями известных писателей. Предлагаем одну историю, напоминающую сказку Андерсена.
Жили-были Единичка и ее подружка – Мнимая Единичка. Они были неразлучны, но Мнимой Единичке всегда хотелось занять место своей подружки. В стране Математике король Цифра решил женить своего сына Нолика.
Позвал он принца к себе и сказал ему:
— Сынок, я уже стар и слаб, и мне сложно управлять страной, пришло время тебе жениться, — начал он свой разговор с сыном.
Невесты королевства услышали эту новость, поспешили во дворец на смотрины.
— Я самая красивая и умная, — сказала Пятерка. – Только я могу быть супругой нового короля!
— Нет, нет, — я умнее и мудрее тебя, — ответила ей Семерка.
Нолик, глядя на девушек, мечтал увидеть среди них ту, единственную Единицу, в которую он давно был безответно влюблен.
Единичке тоже нравился принц, но она была очень стеснительной. Ее опередила подружка — Мнимая Единичка, но принц понял, что это не его возлюбленная, и отверг нахалку. Король, который познакомился с настоящей Единичкой, одобрил выбор сына, и вскоре сыграли свадьбу на всю десятку!
Необычное исцеление
Предлагаем интересный проект «Математические сказки для 3 класса», которые созданы обычными школьниками. В некотором арифметическом царстве жил Король Натуральное число и королева Правильная Дробь. Управлять страной им помогали Деление и Сумма.
У них родилась дочь – Смешанное число, которая была похожа дробной частью на маму, а целой – на папу. Повзрослев, принцесса стала изучать по магической книге заклинания, в итоге она превратилась в Неправильную Дробь. Вернуть девушке прежний облик помог настоящий обряд — она искупалась в волшебном зеркальном озере.
Сказка о порядке в царстве Математики
Вполне можно в виде сказки сделать необычный проект про математические сказки. 3 класс – возраст, в котором ребята искренне верят в волшебные превращения.
Жили в стране Математики двойняшки-Единички. Их родители умерли, девочки остались одни. Рядом с их домом жила вредная старушка-Двойка. Она не любила малышек, придиралась к ним без причины. Однажды в дом сестричек постучали, вошли два юноши, представившиеся пажами короля: Равно и Плюсом.
Когда старуха оказалась на пороге, Плюс встал между сестричками, а Равно оказался сзади их, и тут старушка улыбнулась, она признала в девочках своих внучек.
Спустя некоторое время, подружки вышли замуж за королевских пажей, а старушка Двойка стала для них настоящей доброй феей.
Ссора лучших подружек
Две десятичные дроби: Шесть Сотых и Шесть Тысячных вместе гуляли, играли, но однажды девочки поссорились из-за пустяка.
Шесть Сотых говорит:
– Я намного больше!
Шесть Тысячных ей отвечает:
– Я занимаю больше места на листе.
– Но я больше тебя, – парирует Шесть Сотых.
Не смогли подружки договориться, пошли спрашивать у других цифр. Ноль воскликнул:
– Все хороши! Ты, Шесть Сотых, больше своей подружки. А ты, Шесть Тысячных, занимаешь в школьной тетрадке больше места. И каждая из вас по-своему права.
Девочки внимательно выслушали мудрого Ноля, и решив, что у них нет больше повода для вражды, они помирились.
В заключение
Для того, чтобы стимулировать самостоятельную деятельность по математике младших школьников, оптимальным вариантом будет вовлечение подрастающего поколения в исследовательскую и проектную деятельность. Ребята, изучая разнообразные математические действия, для каждого придумывают сказочные истории, в которых с цифрами происходят самые невероятные приключения.
Например, после изучения определенной темы, младшие школьники могут представить свои творческие работы другим ребятам.
Самые яркие проекты, касающиеся математических вычислений, вполне могут стать базой для организации интересного внеурочного мероприятия.

Мастер-класс:
«Использование
проектной технологии
на уроках математики в начальной школе»
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №2 города Азнакаево» Азнакаевского муниципального района Республики Татарстан
Работу выполнили учителя
начальных классов первой
квалификационной категории
Багманова Раушан Ракитовна
Галиева Фарида Масгутовна.
2018 год

Цель:познакомить слушателей с особенностями организации и проведения проектного занятия по математике.

Задачи :
— осветить современные подходы к организации проектной деятельности школьников;
— систематизировать информацию об отличительных характеристиках и о формах представления результатов проектной деятельности учащихся;
— научить в общих чертах методике постановки проектной деятельности школьников.

Из исследований известно, что учащиеся удерживают в памяти:
— 10% от того, что они читают;
— 26% от того, что они слышат;
— 30% от того, что они видят;
— 50% от того, что они видят и слышат;
— 70% от того, что они обсуждают с другими;
— 80% от того, что основано на личном опыте;
— 90 % от того, что они говорят (проговаривают) в то время, как делают;
— 95% от того, чему они обучаются сами.

Жан- Жак Руссо
заметил, что среди многих тропинок к знанию
самая важная и самая короткая та, что позволяет получать знания с затруднениями. !

«Опыт преодоления дает личности возможность полноценно развиваться, помогает становлению тех качеств, которые нужны для того, чтобы быть успешным в жизни». Л.В.Занков.

В начальной школе математика является основой развития у учащихся познавательных действий, в первую очередь логических, включая и знаково-символические, а также таких, как планирование (цепочки действий по задачам), систематизация и структурирование знаний, преобразование информации, моделирование, дифференциация существенных и несущественных условий, аксиоматика, формирование элементов системного мышления, выработка вычислительных навыков. Особое значение имеет математика для формирования общего приема решения задач как универсального учебного действия. Таким образом, математика является эффективным средством развития личности школьника. Ученики в процессе последовательного выполнения различных заданий смогут зафиксировать в наглядно-логичной форме содержание изучаемого материала. Игровые формы работы: игры, загадки, задачи на смекалку дают возможность усвоению нового материала.
Метод проектов всегда ориентирован на самостоятельную деятельность учащихся — индивидуальную, парную, групповую, которую учащиеся выполняют в течение определенного отрезка времени.

Когда речь идет о проектной деятельности, индивидуальной или групповой, необходимо, чтобы целью познавательных действий учащихся было не просто усвоение содержания, а решение определенной проблемы на основе этого содержания, т.е. активное применение получаемых знаний либо для получения нового знания, либо для получения практического результата на основе применения полученного знания.
Ученики должны четко представлять себе, как можно использовать полученные ими теоретические результаты на практике.

В основе методов проектов лежит развитие познавательных навыков учащихся, умения самостоятельно конструировать свои знания, умения ориентироваться в информационном пространстве, анализировать полученную информацию, самостоятельно выдвигать гипотезы, умения принимать решения (поиск направления и методов решения проблемы); развитие критического мышления, умения исследовательской, творческой деятельности. Этот подход ограничено сочетается с групповым подходом к обучению. Собственно обучение в сотрудничестве является как бы частью метода проектов.

Какие
бывают
типы
проектов?

а) Исследовательские. Такие проекты требуют хорошо продуманной структуры, обозначенных целей, актуальности проекта для всех участников, продуманных методов, в том числе экспериментальных и опытных работ, методов обработки результатов. Пример: проекты для старшеклассников: эссе, исследовательские рефераты.
б) Творческие. Такие проекты, как правило, не имеют детально проработанной структуры, она только намечается и далее развивается, подчиняясь логике и интересам участников проекта. Пример: газета, видеофильм, спортивная игра, подготовка выставки.

в) Игровые. В таких проектах структура также только намечается и остается открытой до окончания проекта. Участники принимают на себя определенные роли, обусловленные характером и содержанием проекта. Это могут быть литературные персонажи или выдуманные герои, имитирующие социальные или деловые отношения, осложняемые придуманными участниками ситуациями. Результаты таких проектов могут намечаться в начале проекта, а могут вырисовываться лишь к его концу. Степень творчества здесь очень высокая, но доминирующим видом деятельности все-таки является ролево-игровая, приключенческая. Пример: сценарий праздника эпохи, фрагмент урока, кроссворды.

г) Информационные проекты. этот тип проектов изначально направлен на сбор информации о каком-то объекте, ознакомление участников проекта с этой информацией, ее анализ и обобщение фактов, предназначенных для широкой аудитории. Пример: различные сообщения, доклады.
д) Практико-ориентированные. Эти проекты отличает четко обозначенный с самого начала предметный результат деятельности участников проекта. Причем этот результат обязательно ориентирован на интересы самих участников. Такой проект требует хорошо продуманной структуры, даже сценария всей деятельности его участников с определением функций каждого из них, четкие выводы и участие каждого в оформлении конечного продукта. Здесь особенно важна хорошая организация координационной работы. Пример: проект закона, справочный
материал, программа действий,
совместная экспедиция,
наглядное пособие.

Проекты в 1 классе по темам:
1). «Математика вокруг нас. Числа в загадках, пословицах, поговорках». (Работа проводится в течение всего полугодия.)
2). «Математика вокруг нас. Форма, размер, цвет. Узоры и орнаменты».
Проекты во 2 классе.
Математика.
1). « Математика вокруг нас. Узоры на посуде».
2). « Оригами».
Проекты в 3 классе.
Математика.
1). «Математические сказки».
2). «Задачи – расчёты».
Проекты в 4 классе.
Математика.
1). «Математика вокруг нас». Создание математического справочника «Наш город (село)».
2). «Математика вокруг нас». Составление сборника математических задач и заданий.

Проектные работы
учащихся.

Этапы работы над проектом :
1.Определение темы, цели проекта.
2. Формирование групп, планирование, распределение труда (выбор методов и объектов исследования).
3. Исследование проблемы на основе распределения труда.
4.Оформление проектных материалов.
5.Презентация (защита) проекта.
6. Оценка результатов и процесса проектной деятельности. Презентация работ.

Проект на тему :
“Задачи-расчёты “.
Цели проекта:
Рассмотреть и решить задачи-расчёты, которые используются в повседневной жизни человека.
Задачи проекта:
Проанализировать жизненные ситуации
в семье и выявить из них задачи-расчеты.
Составить и решить эти задачи.

1 группа: «Обои ».
2 группа: «Плинтусы».
3 группа: «Краска для
покрытия пола».
4 группа: «Бордюры».

Попробуйте рассчитать
свой рабочий день.
5 уроков
Занятия с одарёнными детьми-
1 час
Совещание при директоре-
1 час 20 минут
Посещение семьи.

Творческое задание.
Каждая группа придумывает
свою задачу-расчёт,
с которой сталкивается
в жизни.

ВЫВОД. На таких уроках у учащихся развивается умение применять полученные знания в нестандартных ситуациях, при решении творческих и логических заданий, а также развивается воображение, наблюдательность, любознательность, логическое и образное мышление, расширяется кругозор и словарный запас.
При использовании проектной технологии задача учителя многократно усложняется. Теперь он не просто объясняет новый материал, а создает ситуацию, когда дети сами его «откроют» для себя. Таким образом, ребенок становится в позицию своего обучения и, как результат, у него образуются новые знания, он овладевает новыми способами действия. У учащихся формируются такие мыслительные операции как анализ, синтез, оценка и рефлексия. Учитель перестает выполнять просто информационные функции, а становится управленцем, организующим самостоятельную познавательную деятельность детей.

Рефлексия.
Закончите предложение:
На мастер классе я……………
Самым интересным сегодня для меня было……….
В своей дальнейшей работе я ……………
Я пожелал бы ведущему мастер класс…………….

3 класс
Математика вокруг нас

Цель работы:
Выяснить, какую роль играет математика в жизни человека

Задачи:
1.Изучить историю развития счета.
2. Изучить историю возникновения цифр и чисел.
3. Подобрать и классифицировать пословицы, сказки, песни, загадки, в которых встречаются числа
4. Найти в окружающем мире предметы, имеющие форму геометрических фигур или геометрический орнамент.
5.Оформить стенгазеты.
6.Выпустить книгу собственных сказок о числах.

Гипотеза:
Математика
помогает познавать окружающий мир и другие науки .

Методы исследования:
1.Наблюдение
2.Анкетирование
3.Сравнение
4.Анализ
5.Моделирование
6.Сбор и обработка информации

Михайлова Руслана
Историки

Цель:
Узнать историю чисел и цифр и
понять как люди научились считать.

Задачи:
Изучить информацию по данной теме.
Научиться записывать числа числовыми знаками разных народов.
Провести опрос учащихся.

История развития счета.
К современным цифрам люди шли много столетий. В древности для запоминания чисел люди пользовались зарубками на камнях, деревьях и палках, а также узлами на верёвках.
Была целая наука о завязывании сложных двойных и тройных узлов, которые обозначали разные числа. Это была очень неудобная запись.

Узлы, которые применяли для изображения чисел

Как люди научились считать?
Давным –давно наши далекие предки жили племенами. Их жизнь мало чем отличалась от жизни животных. Первобытные люди, так же как и маленькие дети не знали счета. Наблюдая окружающую природу , от которой полностью зависела их жизнь, наши предки из множества различных предметов научились выделять отдельные предметы. Поначалу они определяли это соотношение как «много», «один». Пальцы рук сыграли немалую роль в истории счета.

Счет папуасов на островах Тихого океана
«Излюбленный способ счета состоит в том, что папуас загибает один за другим пальцы руки, причем издает определенный звук, например «бе-бе-бе»… Досчитав до пяти, он говорит «ибон-бе» (рука). Затем он загибает пальцы другой руки, снова повторяет «бе-бе-бе»… пока не доходит до «ибон-али» (другой руки). Затем он идет дальше, приговаривая «бе-бе», пока не доходит до «самба-бе» и «самба-али» (одна нога, две ноги). Если нужно считать дальше папуас пользуется пальцами рук кого-нибудь другого».Миклухо-Маклай

Появление знаковых систем
Около 6000 лет назад в мире появились наиболее важные знаковые системы:
счёт;
письменность;
карта.
Люди поняли, что знак – это самый удобный способ передачи информации.
Знаки помогали людям сохранять и накапливать полученные знания.
Так появились книги, приборы, различные достижения науки и техники.

Десятичная система счисления
И вот около 5000 лет назад почти одновременно в разных странах – Вавилоне, Египте и Китае – появился новый способ записи чисел.
Как бы ни было велико число , его можно записать с помощью всего лишь из десяти знаков – цифр: 1,2,3,4,5,6,7,8,9,0. Каждое число состоит из ступенек: единиц, десятков, сотен, тысяч и т.д.
Принятый сегодня почти у всех народов мира способ счёта группами по 10 называют десятичной системой счисления. Она связана со счётом на десяти пальцах.

Числовые знаки разных народов

Египетские иероглифы
В древнем Египте использовались иероглифы:

Римские цифры
Римские цифры также не очень удобны, но мы и сейчас их используем, например, на циферблате часов, обозначаем век (XXI), размеры одежды (XL).
Каждая из семи римских цифр, где бы она ни стояла, обозначает одно и тоже число. Например, число V обозначает 5 единиц и в числе VI, и в числе IV.

Арабские числа
В наших современных цифрах главное значение имеет позиция в числе. Например, в числе 15 цифра 5 – это 5 единиц, а в числе 53 -5 десятков. Поэтому наша нумерация называется позиционной.
Она возникла в Индии около 1500 лет назад, потом её переняли арабы, а у арабов – европейцы.
Современные цифры теперь называются арабскими.
В России ими пользуются с XVII века

Славянская алфавитная нумерация
До XVII века на Руси пользовались славянской алфавитной нумерацией
Пока вместе с реформами Петра I в Россию из Европы не пришла позиционная десятичная система, которой мы пользуемся сейчас.

Человеку постоянно приходилось что – то измерять .
В этом ему помогали меры, которые всегда были с ним.
Сейчас мы их называем старинные меры длины. Они, конечно же, не столь точны как современные, но всё же помогали при измерении предметов. Надо сказать, что иногда и сейчас мы ими пользуемся.

Магия чисел
Впервые мистическое отношение к числам возникло несколько лет назад. Особым почитанием окружены были числа в Древней Греции. Философ Пифагор, утверждал «что числа правят миром». Он считал, что числа несут добро или зло, счастье и несчастье
1-символ славы и могущества, действия и честолюбия.
2 –это символ любви и непостоянства, все время находится в поисках высшей гармонии и равновесия.
3 считалось счастливым, магическим, символизирует треугольник: прошлое, настоящее, будущее.
4символом устойчивости и прочности. Она представлена квадратом, стороны которого означают стороны света, четыре времени года, четыре стихии- Огонь, Вода, Воздух, Земля.
Пифагор отводил числу 5 –особое место, считая его самым счастливым числом.
6- удивительное число, т. к. получается в результате сложения или умножения всех чисел, на которые делится.
Большим почетом в древности была окружена семерка. Еще в Древнем Вавилоне было известно 7 планет, к которым причисляли Луну и Солнце. Так родилась семидневная неделя. Названия дней связаны с именами богов. Человек воспринимает окружающий мир через «Семь отверстий»(глаза, уши, рот, нос).
8 -воплощение надежности, совершенства. Разделенное пополам, оно имеет равные части ( 4 и 4), (2,2 и 2,2)
Число 9 имеет добрую славу. Оно является олицетворением достатка, полноты. В нумерологии его считают символом материального успеха.

Опрос учащихся
«Числа в судьбе людей»
Какое число счастливее 7 или 13?».
«7» — 61человек
«13» – 64 человека
Из ответов видно, что большинство опрошенных не являются суеверными людьми.

Считалки
Раз, два, три, четыре. Мы сидели на квартире. Чай пили, булки ели, Позабыли с кем сидели.
Раз , два, три, четыре. Кто не спит у нас в квартире? Всем на свете нужен сон, Кто не спит, тот выйдет вон.
Раз, два, три , четыре, пять, Будем в прятки мы играть. Небо, звезды, луг, цветы. Ты поди-ка поводи.
Раз, два, три , четыре, пять. Мы собрались поиграть. К нам сорока прилетела И тебе водить велела.

Скороговорки
Три сороки тараторки, тараторили на горке.
У четырех черепах по четыре черепашонка.
Шесть мышат в шалаше шуршат.
По утру мой брат Кирилл трех крольчат травой кормил.
Восемь сцепщиков сцепляют цистерны.
Сидели, свистели семь свирестелей.

Песни
Тридцать три коровы
Автор текста (слов):
Олев Н.
Композитор (музыка):
Дунаевский М.
«Дважды два четыре»
Автор текста (слов):
Пляцковский М.
Композитор (музыка):
Шаинский В.
«Нам учитель задаёт
с иксами задачи.
Кандидат наук и тот
над задачей плачет»
(Слова ) И. Шаферана
«Три белых коня»
Л. Автор текста (слов): Крылатов Е.
Композитор (музыка): Дербенев

1.Как проснулся, так вставай, лени воли не давай. 2.Лепесток роса умыла, а тебя умоет мыло.
3. Понукания не жди, в школу вовремя ходи.
4.Прежде чем захлопнуть дверь, все ли взял с собой, проверь.
5.В школе, в классе не сори, а насоришь- подбери.
6.Не таскай в кармане мела, это милый мой не дело.
7.Будь в одежде аккуратен, избегай и дыр и пятен.
8.На уроках не болтай, как заморский попугай.
9.Ты сиди за партой стройно, и веди себя достойно.
10.Содержи всегда в порядке, книжки , ручки и тетрадки.
Мы ,друзья ,для вас составим 10 очень важных правил

Много стихотворений, пословиц , загадок, сказок, крылатых выражений про числа и цифры мы узнали, создавая этот проект. Мы открыли для себя много нового и интересного, полезного и нужного, а главное, поняли, что математика- действительно Царица всех наук. Она окружает нас всюду и с ней надо обязательно дружить.
Праздник числа

Опрос учащихся
Математика- любимый предмет- 55%
Математика – необходимый предмет – 90%









 )
)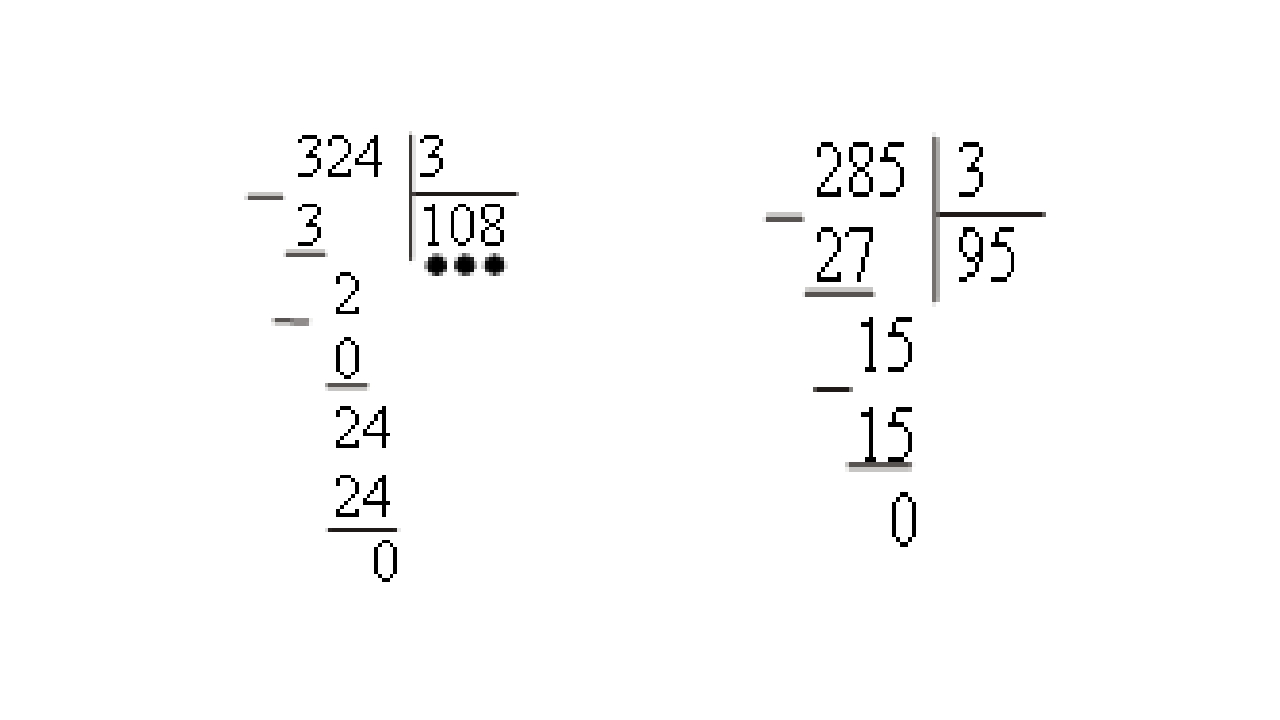
 ) Учитель прикрепляет к началу алгоритма дополнительный шаг.
) Учитель прикрепляет к началу алгоритма дополнительный шаг.

 Много задач, но мало записи… Мы работаем с …(«Блиц – турниром») на с.26, № 7.
Много задач, но мало записи… Мы работаем с …(«Блиц – турниром») на с.26, № 7. Один ученик выходит к доске, снимает (стирает) лишние выражения, объясняет задачу по выбранному им выражению.
Один ученик выходит к доске, снимает (стирает) лишние выражения, объясняет задачу по выбранному им выражению. Перечислите шаги учебной деятельности. (Мы сначала узнали, что не знаем и сами нашли способ).
Перечислите шаги учебной деятельности. (Мы сначала узнали, что не знаем и сами нашли способ). 25 № 4 (нерешенное уравнение по нашей теме), стр. 26 № 6
25 № 4 (нерешенное уравнение по нашей теме), стр. 26 № 6

 После того, как закончат приветствие, берутся за руки и, подняв их вверх, показывают учителю готовность работать.
После того, как закончат приветствие, берутся за руки и, подняв их вверх, показывают учителю готовность работать.
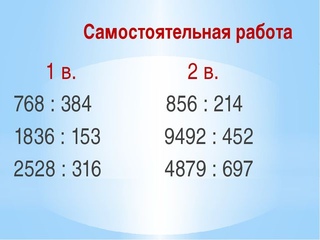
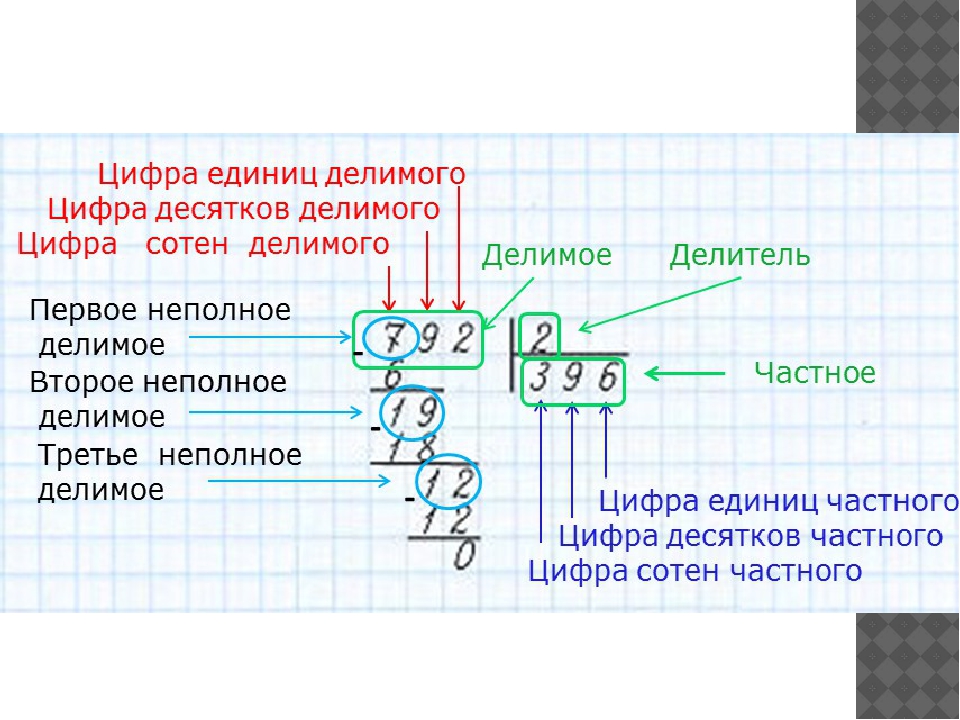 28:4=7, потом нуль переносим в частное.
28:4=7, потом нуль переносим в частное. Проверьте, определите, что неправильно и объясните, на что нужно обратить внимание, чтобы не было таких ошибок.
Проверьте, определите, что неправильно и объясните, на что нужно обратить внимание, чтобы не было таких ошибок. 56 заменяем суммой удобных слагаемых 40 и 16. 40:4=10, 16:4=4, 10+4=14.Пишем в частное 14 и переносим туда же нуль.
56 заменяем суммой удобных слагаемых 40 и 16. 40:4=10, 16:4=4, 10+4=14.Пишем в частное 14 и переносим туда же нуль. :2=3 с.
:2=3 с.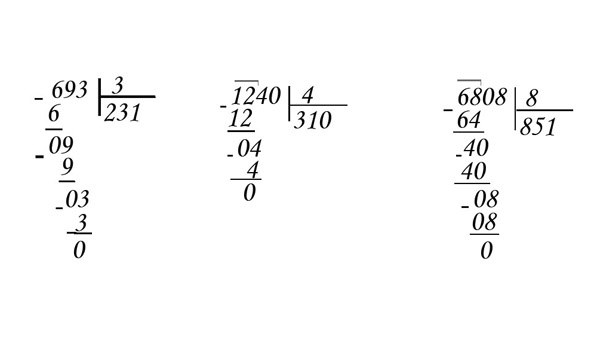


 Остальные решают самостоятельно и в случае затруднения могут попросить помощь, просигналив красным цветом «светофора».
Остальные решают самостоятельно и в случае затруднения могут попросить помощь, просигналив красным цветом «светофора».
 № 10 на стр. 21 выполняем в парах.
№ 10 на стр. 21 выполняем в парах. Спросите себя, как я работал? Все ли понял? Чему научился? Оцените себя.
Спросите себя, как я работал? Все ли понял? Чему научился? Оцените себя.





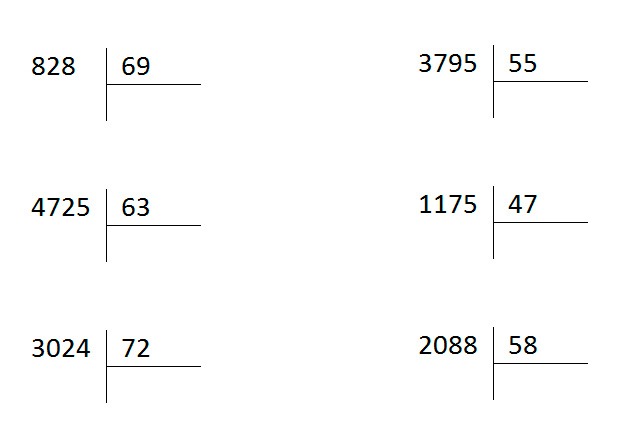
 За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров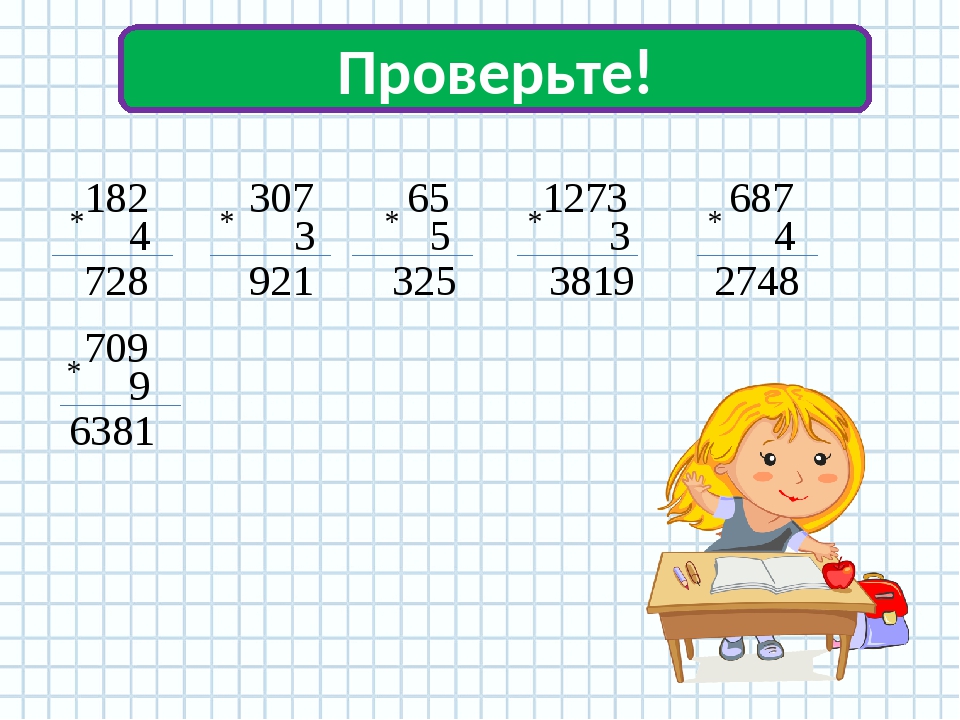





 Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
В таблице наглядно видно, что в число 35 входит 4 раза число 8.