Число пи в эксель как пишется

В данной статье будет рассмотрена та часть математических функций, которая наиболее часто применяется в решении различных задач. С полным перечнем можно ознакомиться на вкладке «Формулы» => выпадающий список «Математические»:

Какие функции затронет статья:

Функции, связанные с округлением:
- ОКРУГЛ;
- ОТБР;
- ОКРУГЛВВЕРХ;
- ОКРУГЛВНИЗ;
- ОКРУГЛТ;
- ОКРВВЕРХ.МАТ;
- ОКРВНИЗ.МАТ;
- ЦЕЛОЕ;
- ЧЁТН;
- НЕЧЕТ.
Суммирование и условное суммирование:
- СУММ;
- СУММПРОИЗВ;
- СУММЕСЛИ;
- СУММЕСЛИМН.
Функции, связанные с возведением в степень и извлечением корня:
- КОРЕНЬ;
- СУММКВРАЗН;
- СУММКВ;
- СУММСУММКВ;
- СУММРАЗНКВ.
Функции случайных чисел и возможных комбинаций:
- СЛУЧМЕЖДУ;
- СЛЧИС;
- ЧИСЛКОМБ;
- ФАКТР.
Функции, связанные с делением:
- ЧАСТНОЕ;
- ОСТАТ;
- НОД;
- НОК.
Преобразование чисел:
- ABS;
- РИМСКОЕ.
Иные функции:
- ЗНАК;
- Число ПИ;
- ПРОИЗВЕД.
Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ.

Функции, связанные с округлением

Функция ОКРУГЛ

Осуществляет стандартное округление, а именно округляет число до ближайшего разряда с указанной точностью.

Синтаксис: =ОКРУГЛ(число; число_разрядов), где

Число – обязательный аргумент. Число либо ссылка на ячейку, его содержащую;
Число_разрядов – обязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – округление до целого числа;
- 1 – округление до десятых долей;
- 2 – округление до сотых долей;
- И т.д.

Аргумент может также принимать отрицательные числа:

-1 – округление до десятков;
-2 – округление до сотен;
И т.д.

Пример использования:

=ОКРУГЛ(5,45;0) – формула возвращает значение 5.
=ОКРУГЛ(5,45;1) – формула возвращает значение 5,5.
=ОКРУГЛ(5,45;3) – не меняет число, т.к. указанное число разрядов превышает его точность.
=ОКРУГЛ(5,45;-1) – формула возвращает значение 10.

Функция ОТБР

Отбрасывает дробную часть числа. Отличие от предыдущей функции заключается в том, что число по факту не округляется, а только усекается до указанного разряда.

Синтаксис: =ОТБР(число; [число_разрядов]), где

Число – обязательный аргумент. Число либо ссылка на ячейку с числом;
Число_разрядов – необязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – точность до целого числа;
- 1 – точность до десятых долей;
- 2 – точность до сотых долей;
- И т.д.

Пример использования:

=ОТБР(5,45;0) – формула возвращает значение 5.
=ОТБР(5,85;0) – так же возвращает значение 5.
=ОТБР(5,45;1) – возвращает значение 5,4.
=ОТБР(5,45;3) – формула не меняет число, т.к. указанное количество разрядов превышает его точность.

Функция ОКРУГЛВВЕРХ

Производит округление до ближайшего большего по модулю числа с указанной точностью.

Синтаксис: =ОКРУГЛВВЕРХ(число; число_разрядов), где

Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
Число_разрядов – обязательный аргумент. Указывает, какое количество знаков после запятой необходимо оставить:
- 0 – округление до целого числа;
- 1 – округление до десятых долей;
- 2 – округление до сотых долей;
- И т.д.

Аргумент может также принимать отрицательные числа:

-1 – округление до десятков;
-2 – округление до сотен;
И т.д.

Пример использования:

=ОКРУГЛВВЕРХ(5,001;0) – формула возвращает значение 6.
=ОКРУГЛВВЕРХ(-5,001;0) – формула возвращает значение -6, т.к. -6 по модулю больше, чем -5,001 по модулю.
=ОКРУГЛВВЕРХ(5,45;1) – возвращает значение 5,5.
=ОКРУГЛВВЕРХ(5,45;3) – функция не изменяет число, т.к. требуемая разрядность превышает его точность.
=ОКРУГЛВВЕРХ(5,45;-1) – формула возвращает значение 10.

Функция ОКРУГЛВНИЗ

Аналогична предыдущей функции, за исключением того, то округляет число в меньшую сторону по модулю с указанной точностью.

Пример использования:

=ОКРУГЛВНИЗ(5,99;0) – формула возвращает значение 5.
=ОКРУГЛВНИЗ(-5,99;0) – формула возвращает значение -5, т.к. -5 по модулю меньше, чем -5,99 по модулю.
=ОКРУГЛВНИЗ(5,45;1) – функция возвращает значение 5,4.
=ОКРУГЛВНИЗ(5,45;3) – не меняет число, т.к. указанная разрядность превышает его точность.
=ОКРУГЛВНИЗ(5,45;-1) – формула возвращает значение 0.

Функция ОКРУГЛТ

Округляет число до ближайшего кратного числу, заданного вторым аргументом.

Синтаксис: =ОКРУГЛТ(число; точность), где

Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
Точность – обязательный аргумент. Число, для которого необходимо найти кратное ближайшее к первому аргументу. В случае задания нулевого значения, функция всегда будет возвращать 0.

Знаки двух аргументов должны совпадать, иначе функция вернем ошибку.

Пример использования:

=ОКРУГЛТ(5,45;0) – формула возвращает значение 0.
=ОКРУГЛТ(5,45; 1,45) – возвращает значение 5,8, т.к. 5,8/1,45=4 и это ближе, чем 7,25/1,45=5.
=ОКРУГЛТ(5,45;3) – формула возвращает значение 6, т.к. 6/3=2, ближе, чем 3/3=1.

Функция ОКРВВЕРХ.МАТ

Появилась в Microsoft Excel 2013. Она округляет число до ближайшего большего кратного числу, заданного вторым аргументом.

Синтаксис: =ОКРВВЕРХ.МАТ(число; [точность]; [режим]), где

Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую числовое значение;
Точность – необязательный аргумент. Число, для которого необходимо найти большее кратное, наиболее приближенное к заданному числу. В случае задания данному аргументу нулевого значения, функция всегда будет возвращать 0.
Режим – необязательный аргумент. Принимает число. Если режим не задан либо равно нулю, то округление будет производиться до большего кратного не по модулю. Если же аргумент отличается от 0, то при округлении отрицательных чисел, большим будет считаться кратное наиболее отдаленное от нуля, т.е. по модулю.

Пример использования:

=ОКРВВЕРХ.МАТ(5,45;0) – формула возвращает значение 0.
=ОКРВВЕРХ.МАТ(5,45;4) – формула возвращает значение 8, несмотря на то, что кратное 4 ближе к 5,45.
=ОКРВВЕРХ.МАТ(-5,45;4) – формула возвращает значение -4, т.к. режим не задан, то округление производиться не по модулю.
=ОКРВВЕРХ.МАТ(-5,45;4;1) – формула возвращает значение -8, т.к. аргумент режим отличается от нуля, то округление производиться по модулю.

Функция ОКРВНИЗ.МАТ

Появилась в Microsoft Excel 2013. Она округляет число до ближайшего меньшего кратного числу, заданного вторым аргументом.

Синтаксис: =ОКРВНИЗ.МАТ(число; [точность]; [режим]), где

Число – обязательный аргумент. Число либо ссылка на ячейку, содержащую число;
Точность – необязательный аргумент. Число, для которого необходимо найти меньшее кратное, наиболее приближенное к первому аргументу. В случае задания нулевого значения, функция всегда будет возвращать 0.
Режим – необязательный аргумент. Принимает число. Если данное число отсутствует либо равно нулю, то округление будет производиться до меньшего кратного не по модулю. Если же аргумент отличается от 0, то при округлении отрицательных чисел, меньшим будет считаться кратное наиболее приближенное к нулю, т.е. по модулю.

Обращаем внимание на то, что третьи аргументы функций ОКРВВЕРХ.МАТ и ОКРВНИЗ.МАТ, не смотря на то, что очень похожи, все же отличаются, т.к. имеют противоположный эффект. Для избавления от путаницы можно прибегать к следующей ассоциации:

Если режим для функции ОКРВВЕРХ.МАТ равен 0, то направление округления к нулю, т.к. аргумент действует только на отрицательные числа;
Если режим для функции ОКРВНИЗ.МАТ равен 0, то направление округления от нуля.

Пример использования:

=ОКРВНИЗ.МАТ(5,45;0) – формула возвращает значение 0.
=ОКРВНИЗ.МАТ(5,45;3) – формула возвращает значение 3, несмотря на то, что кратное 6 ближе к 5,45.
=ОКРВНИЗ.МАТ(-5,45;3) – возвращает значение -6, т.к. режим не задан, то округление производиться не по модулю.
=ОКРВНИЗ.МАТ(-5,45;4;1) – функция возвращает значение -4, т.к. аргумент режим принимает не равен 0, то округление производиться по модулю.

Функция ЦЕЛОЕ

Округляет число до целого в меньшую сторону.

Синтаксис: =ЦЕЛОЕ(число), где число – обязательный аргумент, принимающий числовое значение либо ссылку на ячейку с числовым значением.

Пример использования:

=ЦЕЛОЕ(5,85) – формула вернет значение 5.
=ЦЕЛОЕ(-5,85) – вернет значение -6.

Функция ЧЁТН

Округляет число до ближайшего большего по модулю четного числа.

Синтаксис: =ЧЁТН(число), где число – обязательный аргумент. Принимает числовое значение либо ссылку на ячейку, содержащую число.

Пример использования:

=ЧЁТН(6,85) – вернет значение 8.
=ЧЁТН(-6,85) – вернет значение -8.

Функция НЕЧЁТ

Аналогична функции ЧЁТН за исключением того, что числа округляются до нечетных.

Пример использования:

=НЕЧЁТ(5,85) – вернет значение 7.
=НЕЧЁТ(-5,85) – вернет значение -7.

Суммирование и условное суммирование

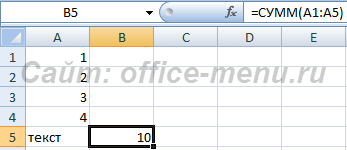
Функция СУММ

Суммирует свои аргументы. Максимальное число аргументов 255.

Если функция ссылается на ячейку, диапазон ячеек или массив, содержащий текстовые либо логические значения, то такие значения игнорируются. Если какой-либо аргумент принимает константу (значение введенное руками), содержащую текстовое значение, то такой аргумент возвращает ошибку, в результате чего вся формула вернет ошибку.

Если же в качестве аргумента функции принимается константа с логическим значением, то ЛОЖЬ приравнивается к нулю, а ИСТИНА к единице.

Синтаксис: =СУММ(число1; [число2]; …), где

Число1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку или диапазон ячеек, содержащих число;
Число2 и последующие аргументы – необязательные аргументы, аналогичные первому.

Пример использования:

В данном примере значение ячейки A5 игнорируется.

=СУММ(1;2;3;4;»текст») – данный вариант вернет ошибку #ЗНАЧ!, т.к. последний аргумент явно принимает текстовое значение.
=СУММ(ИСТИНА;ЛОЖЬ) – формула вернет значение 1.

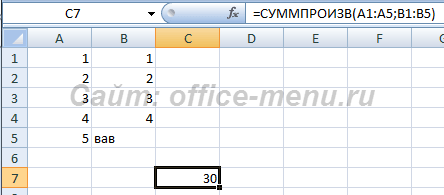
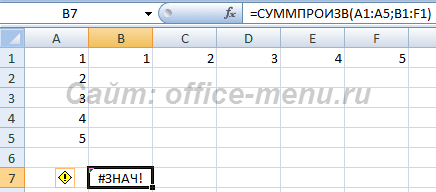
Функция СУММПРОИЗВ

Производит суммирование произведений массивов либо диапазонов.

Если аргументы принимают диапазоны либо массивы, содержащие текстовые или логические значения, то такие значения игнорируются.

Если в аргументе явно задать логическое либо текстовое значение или ссылку на одну ячейку, содержащую такое значение, то вся формула вернет ошибку.

Синтаксис: =СУММПРОИЗВ(массив1; [массив2]; …), где

Массив1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку, диапазон ячеек или массив, содержащих числовое значение;
Массив2 и последующие аргументы – необязательные аргументы, аналогичные первому.

Все аргументы функции должны иметь одинаковую размерность, т.е. если один аргумент ссылается на диапазон с 5 ячейками, то и остальные аргументы должны иметь по 5 элементов. Также должны использоваться диапазоны и массивы одних типов, т.е. горизонтальные и вертикальные массивы и диапазоны либо двумерные и одномерные массивы не могут использоваться одновременно в данной функции, иначе она возвратит ошибку. Чтобы лучше понять этот абзац, ознакомьтесь со статьей «Массивы Excel».

Пример использования:

В данном примере один диапазон содержит текст, но функция игнорирует данное значение и возвращает сумму произведений остальных элементов.

В данном случае формула возвращает ошибку, потому что, не смотря на одинаковое количество элементов в двух диапазонах, они имеют разные типы, т.е. A1:A5 – вертикальный диапазон, а B1:F1 – горизонтальный диапазон.

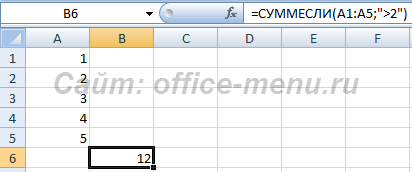
Функция СУММЕСЛИ

Возможно, одна из самых полезных функций, по мнению office-menu. Она производит суммирование элементов, которые соответствуют заданным условиям.

Синтаксис: =СУММЕСЛИ(диапазон_условия; критерий;[диапазон_суммирования]), где

диапазон_условия – обязательный атрибут. Ссылка на ячейку или диапазон ячеек, которые необходимо проверить на совпадение с условием;
критерий – обязательный атрибут. Содержит в себе конкретное значение либо условие для проверки. Условия типа больше, меньше, равно либо их комбинации всегда заключаются в кавычки.
диапазон_суммирования – необязательный атрибут. Ссылка на ячейку либо диапазон ячеек, которые необходимо просуммировать в случае, если элемент диапазона условия подходит под критерий. Если аргумент не указан, то по умолчанию он принимает значение первого аргумента. Также, если диапазон указан не правильно, т.е. для вертикального диапазона условия, указан горизонтальный диапазон суммирования, то последний заменяется на вертикальный, не меняя своего первого элемента, т.е. претерпевает транспонирование.

Пример использования:

В данном примере производится суммирование чисел, которые больше 2. Так как диапазон суммирования не указан, то по умолчанию принимает диапазон условия.

В следующем примере используются разные типы диапазонов, поэтому 3 аргумент меняет ссылку с A1:B1 на A1:A2, и функция возвращает значение 2.

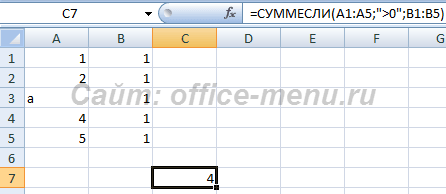
При совместном использовании текстовых и числовых значений в диапазоне условия, проверяться будут либо те, либо другие. Рассмотрите последние два примера.

В первом случае, необходимо произвести суммирование по B1:B5, если элемент из A1:A5 больше нуля. Возвращаемое значение 4, так как текстовый элемент A3 игнорируется.

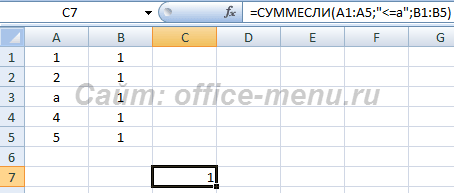
Теперь изменим условие и найдем сумму, если элементы для условия больше или равняются «а». По условиям сортировки все числа являются меньшими любым буквам, поэтому результат должен быть 5. Но так как в условии задано сравнение с текстовой строкой, то все числовые значения отбрасываются. Чтобы они учитывались, их необходимо перевести в текстовый формат. Также можно использовать массивы, для лучшего контроля перевода чисел в текст – {=СУММ(ЕСЛИ(ТЕКСТ(A1:A5;0)<=»а»;B1:B5;0))}.

Функция СУММЕСЛИМН

Выполняет те же действия, что и СУММЕСЛИ, но может проверять различные условия по нескольким диапазонам.

Синтаксис: =СУММЕСЛИМН(диапазон_суммирования; диапазон_условия1; критерий1; [диапазон_условия2]; [критерий2]; …), где аргументы в точности совпадают с аргументами функции СУММЕСЛИ, за исключением того, что диапазон суммирования и первая пара диапазон условия — критерий являются обязательными аргументами. Все последующие пары (от диапазон_условия2; критерий2 до диапазон_условия127; критерий127) необязательны.

Также в данной функции не происходит никаких подмен диапазонов, поэтому все заданные в функции диапазоны должны быть равны по размерности и иметь один тип, т.е. только горизонтальные либо только вертикальные.

Пример использования:

Необходимо узнать сумму ячеек, удовлетворяющих условиям:

По A1:A5 больше 2;
По B1:B5 меньше или равно “г”.

Таким образом, по первому критерию подходят 3 ячейки, по второму 4, но ячеек, которые подходят под оба условия две – C3 и C4. Поэтому формула вернет значение 2.

Функции, связанные с возведением в степень и извлечением корня

Функция КОРЕНЬ

Извлекает квадратный корень из числа.

Синтаксис: =КОРЕНЬ(число), где аргумент число – является числом, либо ссылкой на ячейку с числовым значением.

Пример использования:

=КОРЕНЬ(4) – функция вернет значение 2.

Если возникает необходимость извлечь из числа корень со степенью больше 2, данное число необходимо возвести в степень 1/(показатель корня). Например, для извлечения кубического корня из числа 27 необходимо применить следующую формулу: =27^(1/3) – результат 3.

Функция СУММКВРАЗН

Производит суммирование возведенных в квадрат разностей между элементами двух диапазонов либо массивов.

Синтаксис: =СУММКВРАЗН(диапазон1; диапазон2), где первый и второй аргументы являются обязательными и содержать ссылки на диапазоны либо массивы с числовыми значениями. Текстовые и логические значения игнорируются.

Вертикальные и горизонтальные диапазоны и массивы в данной функции не различаются, но должны иметь одинаковую размерность.

Пример использования:

=СУММКВРАЗН({1;2};{0;4}) – функция вернет значение 5. Альтернативное решение =(1-0)^2+(2-4)^2.

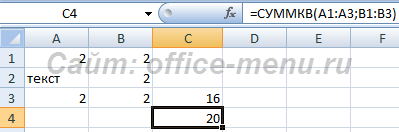
Функция СУММКВ

Воспроизводит числа, заданные ее аргументами, в квадрат, после чего их суммирует.

Синтаксис: =СУММКВ(число1; [число2]), где число1 … число255, число, либо ссылки на ячейки и диапазоны, содержащие числовые значения. Максимальное число аргументов 255, минимальное 1. Все текстовые и логические значения игнорируются, за исключением случаев, когда они заданы явно. В последнем случае текстовые значения возвращают ошибку, логические 1 для ИСТИНА, 0 для ЛОЖЬ.

Пример использования:

=СУММКВ(2;2) – функция вернет значение 8.
=СУММКВ(2;ИСТИНА) – возвращает значение 5, так как ИСТИНА приравнивается к единице.

В данном примере текстовое значение игнорируется, так как оно задано через ссылку на диапазон.

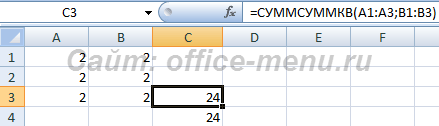
Функция СУММСУММКВ

Возводит все элементы указанных диапазонов либо массивов в квадрат, суммирует их пары, затем выводит общую сумму.

Синтаксис: =СУММСУММКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.

Функция при обычных условиях возвращает точно такой же результат, как и функция СУММКВ. Но если в качестве элемента одного из аргументов будет указано текстовое или логическое значение, то проигнорирована будет вся пара элементов, а не только сам элемент.

Пример использования:

Рассмотрим применение функции СУММСУММКВ и СУММКВ к одним и тем же данным.

В первом случае функции возвращают один и тот же результат:

Алгоритм для СУММСУММКВ =(2^2+2^2) + (2^2+2^2) + (2^2+2^2);
Алгоритм для СУММКВ =2^2 +2 ^2 + 2^2 + 2^2 + 2^2 + 2^2.

Во втором случае функции вернут разные результаты из-за несущественных различий в алгоритме вычисления (части выделенные красным игнорируются, т.к. возвращают ошибку):

Алгоритм для СУММСУММКВ =(2^2+2^2) + (текст^2+2^2) + (2^2+2^2);
Алгоритм для СУММКВ =2^2 +2 ^2 + «текст»^2 + 2^2 + 2^2 + 2^2.

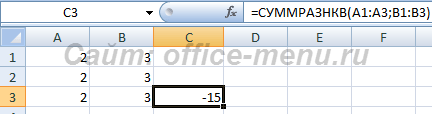
Функция СУММРАЗНКВ

Аналогична во всем функции СУММСУММКВ за исключение того, что для пар соответствующих элементов находится не сумма, а их разница.

Синтаксис: =СУММРАЗНКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.

Пример использования:

Функции случайных чисел и возможных комбинаций

Функция СЛЧИС

Возвращает случайно сгенерированное число в пределах: >=0 и <1. При использовании нескольких таких функций, возвращаемые значения не повторяются.

Синтаксис: =СЛЧИС(), функция не имеет аргументов.

Пример использования можно посмотреть в описании следующей функции.

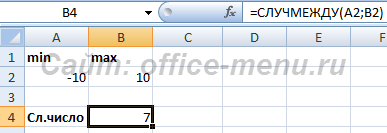
Функция СЛУЧМЕЖДУ

Возвращает случайно сгенерированное целое число в пределах указанных границ. При использовании нескольких таких функций, возвращаемые значения могут повторяться.

Синтаксис: =СЛУЧМЕЖДУ(нижняя_граница; верхняя_граница), где аргументы являются числами, либо ссылками на ячейки, содержащие числа. Все аргументы обязательны, и представляют собой минимальное и максимальное возможные значения соответственно. Аргументы могут быть равны друг другу, но минимальная граница не может быть больше максимальной.

Пример использования:

Значение возвращаемое функцией меняется каждый раз, когда происходит изменение книги.

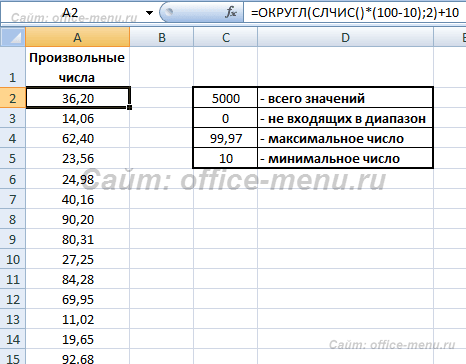
Если вдруг возникнет необходимость возвращать дробные числа, то это можно сделать с использованием функции СЛЧИС по следующей формуле:

=СЛЧИС()*(макс_граница-мин_граница)+мин_граница

В следующем примере возвращаются 5000 произвольных значений, лежащих в диапазоне от 10 до 100. В дополнительно приведенной таблице можно посмотреть минимальные и максимальные возвращенные значения. Также для части формулы используется округление. Оно использовано для того, чтобы увеличить вероятность возврата крайних значений диапазона.

Функция ЧИСЛКОМБ

Возвращает возможное число уникальных комбинаций для определенного количества элементов из общего набора элементов.

Синтаксис: =ЧИСЛКОМБ(размер_набора; колво_элементов), где

размер_набора – обязательный аргумент. Число либо ссылка на ячейку, содержащую число, которое указывает, сколько элементов всего находится в наборе;
колво_элементов – обязательный аргумент. Число либо ссылка на ячейку, содержащую число, которое указывает, какое количество элементов из общего набора должно присутствовать в одной комбинации. Данный аргумент должен равняться либо не превышать первый.

Все аргументы должны содержать целые положительные числа.

Пример использования:

Имеется набор из 4 элементов – ABCD. Из него необходимо составить уникальные комбинации по 2 элемента, при условии что в комбинации элементы не повторяются и их расположение не имеет значения, т.е. пары AB и BA являются равнозначными.

Решение:

=ЧИСЛКОМБ(4;2) – возвращаемый результат 6:

Функция ФАКТР

Возвращает факториал числа, что соответствует числу возможных вариаций упорядочивания элементов группы.

Синтаксис: =ФАКТР(число), где число – обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую числовое значение.

Пример использования:

Имеется набор из 3 элементов – ABC, который можно упорядочить 6 разными способами:

ABC;
ACB;
BAC;
BCA;
CAB;
CBA.

Используем функцию, чтобы подтвердить данное количество: =ФАКТР(3) – формула возвращает значение 6.

Функции, связанные с делением

Функция ЧАСТНОЕ

Выполняет самое простое деление.

Синтаксис: =ЧАСТНОЕ(делимое; делитель), где все аргументы являются обязательными и должны представляться числами.

Пример использования:

=ЧАСТНОЕ(8;4) – возвращаемое значение 2.

Можно воспользоваться альтернативой функции: =8/2.

Функция ОСТАТ

Возвращает остаток от деления двух чисел.

Синтаксис: =ОСТАТ(делимое; делитель), где все аргументы являются обязательными и должны иметь числовое значение.

Знак остатка всегда совпадает со знаком делителя.

Пример использования:

Сама функция из-за алгоритма своего вычисления выдает результат обработки чисел с разными знаками, который возможно Вы от нее ожидать не будете. Подробнее:

=ОСТАТ(8;3) – результат выполнения функции 2.
=ОСТАТ(-8;3) – результат выполнения функции 1. Хотя скорее всего Вы будете ожидать результат 2. Так происходит из-за алгоритма функции: =делимое – делитель*ЦЕЛОЕ(делимое/делитель). В связи с тем, что ЦЕЛОЕ округляет дробные значения до меньшего целого, то результат деления (-8/3) равняется -2,6666 и, соответственно, будет округлен до -3, а не до 2, как в случае с положительными числами. Чтобы избавиться от такого эффекта необходимо не округлять число, а просто отбрасывать дробную часть: =делимое – делитель*ОТБР(делимое/делитель).
=-8-3*ОТБР(-8/3) – результат -2.
=ОСТАТ(-8;-3) – функция вернет результат -2.

Функция НОД

Вычисляет наибольший общий делитель для всех аргументов, на который они делятся без остатка. Наибольший делитель всегда целое число.

Синтаксис:

=НОД(число1; [число2]; …). Максимальное число аргументов 255, минимальное 1. Аргументы являются числами, ссылками на ячейки или диапазонами ячеек, которые содержат числа. Значения аргументов должны быть всегда положительными числами.

Пример использования:

=НОД(8;4) – результат выполнения 4.
=НОД(6;4) – результат выполнения 2.

Функция НОК

Вычисляет наименьшее общее кратное для всех аргументов.

Синтаксис и описание аргументов аналогичны функции НОД.

Пример использования:

=НОК(8;4) – результат выполнения 8.
=НОК(6;4) – результат выполнения 12.

Преобразование чисел

Функция ABS

Возвращает модуль числа.

Синтаксис:

=ABS(число), где число обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую число.

Пример использования:

=ABS(-4) – результат 4.

Функция РИМСКОЕ

Преобразует число в строку, представляющую римское число.

Синтаксис: =РИМСКОЕ(число; [формат]), где

Число – обязательный аргумент. Положительное число либо ссылка на ячейку с положительным числом. Если число дробное, то дробная часть отсекается;
Формат – необязательный аргумент. По умолчанию принимает значение 0. Возможные значения:
- 0 – классическое представление римских чисел;
- От 1 до 3 – наглядные форматы представления длинных римских чисел;
- 4 – упрощенный вариант представления длинных римских чисел;
- ИСТИНА — аналогично 0;
- ЛОЖЬ – аналогично 4.

Пример использования:

=РИМСКОЕ(999;0) – результат «CMXCIX»;
=РИМСКОЕ(999;1) – результат «LMVLIV»;
=РИМСКОЕ(999;2) – возвращает «XMIX»;
=РИМСКОЕ(999;3) – результат «VMIV»;
=РИМСКОЕ(999;4) – результат «IM»;
=РИМСКОЕ(999;ИСТИНА) – результат «CMXCIX»;
=РИМСКОЕ(999;ЛОЖЬ) – результат «IM».

Иные функции

Функция ЗНАК

Проверяет знак числа и возвращает значение:

-1 – для отрицательных чисел;
0 – если число равняется 0;
1 – для положительных чисел.

Синтаксис: =ЗНАК(число), где число – обязательный аргумент, являющийся числом либо ссылкой на ячейку, содержащую числовое значение.

Пример использования:

=ЗНАК(-14) – возвращается значение -1.

Функция ПИ

Возвращает значение числа пи, округленное до 14 знаков после запятой – 3,14159265358979.

Синтаксис: =ПИ().

Функция ПРОИЗВЕД

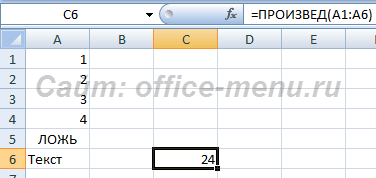
Вычисляет произведение всех своих аргументов. Максимальное число аргументов 255.

Если функция ссылается на ячейку, диапазон ячеек или массив, содержащий текстовые либо логические значения, то такие значения игнорируются. Если какой-либо аргумент явно принимает текстовое значение, то он вызывает ошибку. Если же аргумент явно принимает логическое значением, то ЛОЖЬ приравнивается к нулю, а ИСТИНА к единице.

Синтаксис: =ПРОИЗВЕД(число1; [число2]; …), где

Число1 – обязательный аргумент, являющийся числом либо ссылкой на ячейку или диапазон ячеек, содержащих число;
Число2 и последующие аргументы – необязательные аргументы, аналогичные первому.

Пример использования:

В данном примере видно, что текстовые и логические значения никак не влияют на конечный результат формулы.

Альтернатива использования данной функции — символ звездочки: =2*3*4

Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ()

Данная функция предназначена для работы со структурой промежуточных итогов. Ознакомиться с применением такой структуры можно в соответствующей статье категории Уверенное использование Excel на нашем сайте.

Во время задания подобной структуры, рассматриваемая функция создается автоматически. Смысл ее использования таков, что она игнорирует значения в ячейках, высчитанные с использованием промежуточных итогов. Рассмотрим синтаксис и пример использования.

Синтаксис: =ПРОМЕЖУТОЧНЫЕ.ИТОГИ(номер_функции; ссылка1; [ссылка2]; …), где

номер_функции – обязательный аргумент. Число от 1 до 11 либо от 101 до 111, указывающее на то, какую функцию использовать для расчета и в каком режиме (подробнее читайте ниже);
ссылка1 и последующие ссылки – ссылки на ячейки или диапазоны ячеек, содержащие значения для расчета. Минимальное количество ссылок — 1, максимальное — 254.

Соотношение номера функции с конкретной функцией:

1 – СРЗНАЧ;
2 – СЧЁТ;
3 – СЧЁТЗ;
4 – МАКС;
5 – МИН;
6 – ПРОИЗВЕД;
7 – СТАНДОТКЛОН;
8 – СТАНДОТКЛОНП;
9 – СУММ;
10 – ДИСП;
11 – ДИСПР.

Если к описанным номерам прибавить 100 (т.е. вместо 1 указать 101 и т.д.), то они все равно будут указывать на те же функции. Но отличие заключается в том, что во втором варианте, при скрытие строк, те ячейки, указанные в ссылках, которые будут находится в скрытых строках, участвовать в подсчете не будут.

Пример использования:

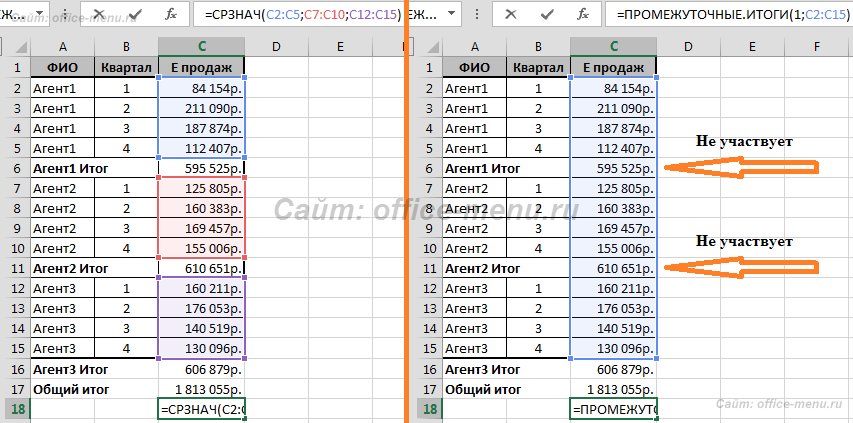
Используем структуру промежуточных итогов, которую мы применяли в одноименной статье. Добавим к ней средний результат по всем агентам за каждый квартал. Для того, чтобы корректно применить функцию СРЗНАЧ для имеющихся значений, нам пришлось бы указать 3 отдельных диапазона, чтобы не принимать в расчет промежуточные значение. Это не составить проблем, если данных не много, но если таблица большая, то выделять каждый диапазон будет проблематично. В данной ситуации лучше применить функцию ПРОМЕЖУТОЧНЫЕ.ИТОГИ, т.к она проигнорирует все ненужные ячейки. Обратите внимание на изображение. Разница очевидна, что второй пример использовать гораздо удобнее при одинаковых результатах функций. Также можно не беспокоиться о добавлении в будущем других строк с итогами.

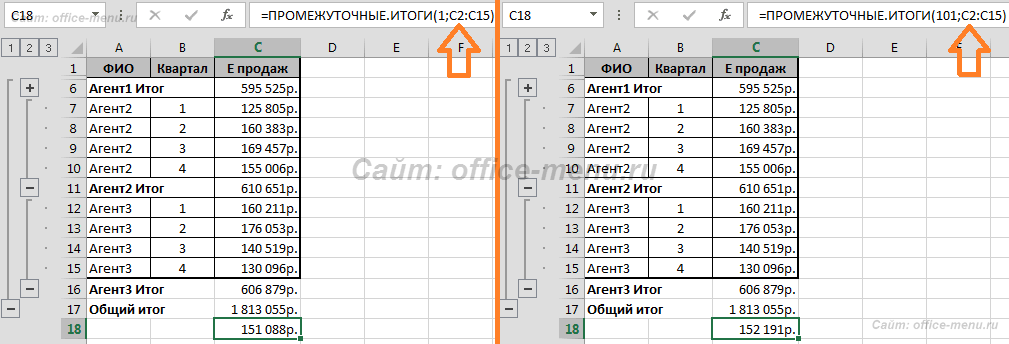
Теперь продемонстрируем различия в использовании режимов функций. В качестве примера используем только что созданную формулу и изменим значение первого аргумента на 101 вместо 1. Возвращаемый результат не измениться до тех пор, пока мы не скроем строки структуры.

Информация продаж по Агенту1 во втором случае не учитывается.

Если материалы office-menu.ru Вам помогли, то поддержите, пожалуйста, проект, чтобы я мог развивать его дальше.

Источник

Обновлено: 08.01.2022

Число Пи как константа или функция, его возвращающая, отсутствуют в VBA, но есть функция Pi рабочего листа Excel, которой можно воспользоваться. А также есть и другие способы расчета значения этого числа.

Функция Pi рабочего листа

Функция Pi рабочего листа Excel возвращает значение числа Пи, округленное до 14 знаков после запятой (3,14159265358979). Присвоение этого значения переменной myPi в коде VBA будет выглядеть следующим образом:

Число Пи через арктангенс

Как известно из геометрии, tg(π/4)=1. Соответственно, π/4=arctg(1), а π=4arctg(1). Используя последнее выражение и учитывая, что функция арктангенс (Atn) в VBA есть, можно не обращаться к соответствующей функции рабочего листа Excel:

Число Пи через арккосинус

Здесь совсем все просто: cos(π)=-1, отсюда π=arccos(-1). Единственная загвоздка только в том, что функции арккосинус в VBA нет и опять приходится обращаться к функции арккосинус (Acos) рабочего листа Excel:

Проверка работы функций

Скопируйте код в модуль VBA и убедитесь в работоспособности представленных выше функций, возвращающих число Пи. Все функции возвращают значение, округленное до 14 знаков после запятой (3,14159265358979):

Создание константы myPi

Если при написании кода VBA Excel часто приходится использовать число Пи, его можно объявить как константу. Объявление следует разместить в разделе Declarations и константа будет доступна во всех процедурах этого модуля:

Объявление константы myPi

Вместо числового значения, присваиваемого константе myPi, можно использовать любую из выше представленных функций.

Содержание рубрики VBA Excel по тематическим разделам со ссылками на все статьи.

2 комментария для “VBA Excel. Число Пи (значение)”

Добрый день!
Именно так (Module1.myPi) можно будет обращаться к константе, если объявить ее в разделе Declarations модуля Module1:

Функция ПИ в Excel, как несложно догадаться, предназначена для вставки числа ПИ на страницу. Значение числа ПИ (3,141592654) вставляется в ячейку с функцией.

видео может дополнять статью или содержать её полностью

Одна из простейших математических функций в Excel, предназначенная для получения известного числа «Пи». Функция ПИ возвращает число с точностью 15-ть знаков после запятой, поэтому если Вам нужна меньшая точность, то используйте настройки формата ячеек Excel, а вот если нужно больше знаков, то ничего не получится.

Формула для получения числа ПИ не имеет никаких настроек, а также не принимает аргументов. Обобщённый синтаксис функции выглядит следующим образом: ПИ()

Функция возвращает следующее значение: 3,141592653589790

Обратите внимание, что по умолчанию в Excel в ячейках применяется формат «Общий», поэтому число символов после запятой будет меньше. Если нужно больше, то поменяйте формат на «Числовой» и установите нужное число знаков после запятой (но более 15-ти всё равно смысла не имеет).

Использование функции ПИ

Для получения числа ПИ в Excel формула не обязательна. Вы, например, можете просто задать константу в какой-то ячейке или задать переменную, установив для неё нужное значение.

Если же Вы решите использовать число ПИ в Excel в формуле и применять для этого встроенную функцию, то обычно это имеет смысл в тех случаях, когда функция ПИ применяется как один из аргументов составных формул.

Допустим, нам нужно вычислить площадь круга. В таком случае составная формула будет такой, как в примере. Сам пример Вы можете скачать после статьи (файл формата Excel) и посмотреть как именно используется ПИ на практике (всё очень просто).

Также Вы можете дополнительно прочитать стандартную справку Excel по рассмотренной формуле (смотрите PDF документ после статьи).

Уникальная метка публикации: 887471AC-EB57-E683-9B81-9F2741FDD110
Источник: //artemvm.info/information/uchebnye-stati/microsoft-office/funkcziya-pi-v-excel/

Смотреть видео
Функция ПИ в Excel

Прикреплённые документы

Файлы для загрузки

Вы можете скачать прикреплённые ниже файлы для ознакомления. Обычно здесь размещаются различные документы, а также другие файлы, имеющие непосредственное отношение к данной публикации.

Пусть радиус окружности равен 1. R = 1 . Впишем в окружность последовательно правильный треугольник, правильный шестиугольник, правильный двенадцатиугольник и т. д. Удваивая на каждом шаге количество сторон правильного многоугольника.

Из курса математики известно, что сторона правильного треугольника, вписанного в окружность, вычисляется по формуле , а сторону каждого следующего многоугольника будем искать по формуле

Формула для вычисления периметра многоугольника .

При увеличении количества сторон правильного многоугольника его периметр будет приближаться к длине окружности, в которую он вписан . Так как длина окружности и число  связаны формулой , при R=1 , откуда . Поэтому для вычисления числа  воспользуемся формулой .

Реализуем алгоритм подсчета числа  в электронной таблице E x cel следующим образом (таблица E xcel находится в режиме отображения формул):

Проанализируем полученный результат. Достоверно известно, что

 = 3,1415926 535 8979323846 2643383279 5028841971 6939937510…..

Удваивая число сторон правильного многоугольника и используя формулу , мы приблизились к числу  = 3,1415926 453212200 с 1 по 17 строки таблицы (с точностью до 7 знаков после запятой), с 17 по 20 строки результат оставался неизменным , а начиная с 21 строки начал отдаляться от истинного и перестал вычисляться совсем.

Excel храненит данные и осуществляет пересчет в формулах с точностью 15 разрядов. Так как Excel оперирует числами в двоичной системе счисления, и для хранения каждого двоичного числа использует 8 байт (64 бита). Поэтому любое десятичное число в Excel может содержать не более 15 значащих цифр. Если ввести десятичное число, содержащее более 15 значащих цифр, то «лишние» цифры просто отбрасываются или заменяются нулями, что мы и наблюдаем в нашей таблице.

Рассмотрим возможности возведения экспоненты в степень и в частности использования числа Е в Excel, также известного как число Эйлера.

Число Е — основание натурального логарифма, математическая константа равная приблизительно 2,71828.
Также данное число называют как число Эйлера или число Непера.
Экспонента — показательная функция f(x) = exp (x) = e x , где е — число Эйлера.
Также в Excel есть возможность использовать другую известную математическую константу — число Пи.

Функция EXP в Excel

Чтобы возвести экспоненту в степень в Excel можно воспользоваться стандартной функцией:

EXP(число)
Возвращает экспоненту заданного числа.

Число(обязательный аргумент) — степень, в которую возводится число Е (приблизительное значение 2,71828182845904).

Для получения числа Е в Excel достаточно в качестве аргумента функции EXP взять значение 1:

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

«Вставить функцию»

Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».

Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».

Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

«Вставка»

«Диаграммы»

«График»

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Отблагодарите автора, поделитесь статьей в социальных сетях.

В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.

Описание

Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.

Синтаксис

Аргументы функции EXP описаны ниже.

Число — обязательный аргумент. Показатель степени, в которую возводится основание e.

Замечания

Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).

Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Читайте также:

Первый электронный цифровой компьютер общего назначения который можно было перепрограммировать

Dr web cureit очень долго сканирует

Как скрыть расширения в edge

Есть ли в оренбурге ростелеком

Инвертор fubag in 170 мигает дисплей

Источник

Пи – одна из самых популярных математических констант, используемых во всех областях математики и физики. Это отношение длины окружности к диаметру круга, которое имеет приблизительное значение 22/7 или 3,14. Вы можете легко написать Пи от руки как строчную греческую букву Пи (π). Однако на клавиатуре нет клавиш по умолчанию для ввода Pi как в Windows, так и в macOS. Если вам нужно часто использовать π в документации, вот как вы можете вводить символы Pi с помощью сочетаний клавиш.

Значение Пи (Изображение предоставлено – Википедия)

Сводка сочетаний клавиш

Прежде чем мы объясним различные методы ввода символов Pi, вот краткое описание сочетаний клавиш.

Название символа	Греческая строчная буква пи (π)
Ярлык альтернативного кода	Alt + 0960
Alt + X (документ Word)	03C0 Alt + X
Ярлык Mac	Option + 03C0
HTML Entity Decimal	Пи
HTML-объект шестнадцатеричный	Пи
Имя объекта HTML	Пи
Значение CSS	03C0;
Последовательность выхода из JS	u03C0
Десятичный	960
Шестнадцатеричный	3C0
Юникод	U+03C0

Введите символ в Windows

Есть несколько способов ввести символ Пи в Windows в зависимости от приложения.

Введите символ Pi с помощью сочетаний клавиш Alt-кода

Если у вас большая клавиатура с отдельной цифровой панелью, то использование сочетаний клавиш с альтернативным кодом – самый простой вариант.

Сначала включите цифровую клавишу и поместите курсор в то место, куда вы хотите вставить символ.
Удерживая одну из клавиш alt, введите 0960 с цифровой клавиатуры.
Это создаст на вашем документе символ Пи π.

Использование метода Alt + X в Word

Это полезный вариант для ввода символов только в документы Microsoft Word. Преимущество здесь в том, что для этого не требуется отдельная цифровая клавиатура.

Нажмите 03C0 и одновременно нажмите клавиши alt + x.
Это преобразует шестнадцатеричное значение в символ Пи, например π.

Ввод символа Pi в приложениях Microsoft Office

В дополнение к вышеуказанному методу alt + x в Word вы можете использовать утилиту Symbol во всех приложениях Microsoft Office, таких как Excel, PowerPoint и Outlook.

Откройте любые другие приложения Office и перейдите в меню «Вставка».
Выберите «Символы> Символ> Дополнительные символы», чтобы открыть утилиту.

Открытые символы в приложениях Office

Измените подмножество на «Греческий и коптский» и найдите символ Пи.
Вы можете дважды щелкнуть, чтобы вставить символ в ваш документ.

Найдите Пи на карте персонажей

Использование редактора формул

Вы можете использовать редактор формул в приложениях Office, если хотите быстро вводить формулы с помощью Пи. Перейдите в «Вставка»> «Символы»> «Уравнение», чтобы открыть редактор формул. Вы можете выбрать такие уравнения, как A = πr2, непосредственно из доступных формул или ввести символ Пи, выбрав его из списка символов «Базовая математика».

Используйте редактор формул для ввода числа Пи

Вы можете использовать опцию автозамены в редакторе формул, набрав «пи», чтобы быстро создать символ. Однако уравнения не похожи на обычный текст в вашем документе. Вы можете правильно выровнять их, чтобы они сочетались с другим контентом, особенно когда вам нужно распечатать.

Введите символ Пи с картой символов

Если ни один из вышеперечисленных методов не работает, вы можете использовать автономное приложение Character Map в Windows.

Введите charmap в поле поиска Windows и откройте приложение «Карта символов».

Открыть карту персонажей

Щелкните «Группировать по» и выберите «Поддиапазон Unicode». Во всплывающем окне выберите вариант «Греческий».
Теперь вы можете увидеть все греческие буквы и нажать на символ греческой строчной буквы Пи.
Нажмите кнопку «Выбрать», а затем «Копировать», чтобы скопировать символ в буфер обмена.
Вы можете вставить скопированный символ в любое приложение.

Символ Пи на карте символов

Использование панели эмодзи в Windows 10

Компьютеры с Windows 10 поставляются с панелью эмодзи, к которой можно получить доступ, нажав сочетания клавиш «Win + Dot». После открытия всплывающего окна нажмите «Символы», а затем «Языковые символы». Здесь вы можете найти символ Пи π и вставить его в любое приложение.

Символ Пи на панели эмодзи Windows

Введите символ Pi в Mac

Также легко ввести символ Пи на Mac, используя один из следующих методов.

Использование ввода шестнадцатеричного кода

Во-первых, вы должны изменить метод ввода с клавиатуры со стандартного ABC на Unicode Hex Input. Вы можете в любое время переключить языковой ввод с верхней панели.

Убедитесь, что метод ввода отображается как U +, что означает ввод в формате Unicode Hex.

Шестнадцатеричный ввод Unicode

Поместите курсор в то место, где вы хотите ввести символ.
Удерживая одну из клавиш выбора на клавиатуре, введите 03C0, чтобы сделать символ Пи π.
Вы можете продолжить ввод с помощью U + или перейти на ABC.

Использование программы просмотра персонажей

Если вы не можете изменить ввод с клавиатуры, следуйте этому методу, чтобы ввести символ Pi с помощью приложения Character Viewer.

Когда вы находитесь в любом приложении, например Pages или Microsoft Word для Mac, перейдите в меню «Правка> Emoji & Symbols». Или вы можете нажать «Command + Control + Space».
Это откроет приложение Character Viewer и щелкните маленькую стрелку, чтобы выбрать опцию «Настроить список…».

Настроить список

Выберите «Греческий» во всплывающем окне и нажмите кнопку «Готово».

Включить греческие буквы

Теперь нажмите на опцию «Греческий» на боковой панели и найдите греческий символ строчной буквы «Пи» π.

Вставить Пи из средства просмотра символов

Дважды щелкните символ, чтобы вставить его в документ.

Введите символ в HTML и CSS

Вы можете использовать десятичные или шестнадцатеричные кодовые точки в приведенном ниже формате для вставки символа Пи в HTML-документы. Кроме того, Pi также имеет имя объекта HTML, которое вы можете использовать.

<p>π</p>
<p>π</p>
<p>π</p>

Точно так же используйте шестнадцатеричное значение, как показано ниже, в вашем CSS, чтобы вставить символ Pi.

li:before {
    content:03C0;
    font-family:Arial;
}

Варианты символов

Символ Пи похож на любые другие текстовые символы в приложениях Windows и Mac. Таким образом, вы можете изменить цвет, размер шрифта и применить к символу текстовые эффекты. Кроме того, приложение Mac Character Viewer предлагает встроенный вариант шрифта для символа. Вы можете выбрать символ, который выглядит как написанный от руки, из сотен доступных вариантов.

Ниже приведены некоторые примеры символа Пи с текстовым эффектом в документе Microsoft Word. Как видите, вы можете применить текстовый эффект, чтобы выделить формулу или уравнение, чтобы их можно было отличить от другого текстового содержимого.

Применение текстовых эффектов к символу Пи

Ниже приведены некоторые другие символы Пи с вариациями. Помните, что в греческом языке также есть заглавная буква Пи Π (alt + 0928) и символ Пи ϖ (alt + 0982), которые отличаются от математического символа Пи (π).

Символы Пи	Имя	Старый код	Alt + X
?	Математический жирный маленький Пи	120529	1D6D1
?	Математический курсив Маленький Пи	120587	1D70B
?	Математический полужирный курсив Маленький Пи	120645	1D745
?	Математический жирный маленький Пи без засечек	120703	1Д77Ф
?	Математический шрифт без засечек, жирный, курсив, маленький, пи	120761	1D7B9

Получение значения Пи

Как уже упоминалось, приблизительное значение Пи составляет 22/7, и ниже приведены некоторые дроби, используемые для вычисления значения Пи.

22 / 7
333 / 106
355 / 113
52163 / 16604
103993 / 33102
104348 / 33215
245850922 / 78256779

Однако Пи – это иррациональное число, не имеющее бесконечных десятичных знаков без повторяющегося шаблона. Люди используют 3,14 как приблизительное значение, и вот первые 100 цифр числа Пи.

3.1415926535897932384626433832795028841971693993751058209749445923078 164062862089986280348253421170679

Вы также можете быстро получить значение Пи, выполнив поиск в Google, который покажет до 11 десятичных знаков.

Значение Пи в Google

Источник записи: webnots.com

Источник

Функции, связанные с округлением

Функция ОКРУГЛ

Функция ОТБР

Функция ОКРУГЛВВЕРХ

Функция ОКРУГЛВНИЗ

Функция ОКРУГЛТ

Функция ОКРВВЕРХ.МАТ

Функция ОКРВНИЗ.МАТ

Функция ЦЕЛОЕ

Функция ЧЁТН

Функция НЕЧЁТ

Суммирование и условное суммирование

Функция СУММ

Функция СУММПРОИЗВ

Функция СУММЕСЛИ

Функция СУММЕСЛИМН

Функции, связанные с возведением в степень и извлечением корня

Функция КОРЕНЬ

Функция СУММКВРАЗН

Функция СУММКВ

Функция СУММСУММКВ

Функция СУММРАЗНКВ

Функции случайных чисел и возможных комбинаций

Функция СЛЧИС

Функция СЛУЧМЕЖДУ

Функция ЧИСЛКОМБ

Функция ФАКТР

Функции, связанные с делением

Функция ЧАСТНОЕ

Функция ОСТАТ

Функция НОД

Функция НОК

Преобразование чисел

Функция ABS

Функция РИМСКОЕ

Иные функции

Функция ЗНАК

Функция ПИ

Функция ПРОИЗВЕД

Функция ПРОМЕЖУТОЧНЫЕ.ИТОГИ()

Функция Pi рабочего листа

Число Пи через арктангенс

Число Пи через арккосинус

Проверка работы функций

Создание константы myPi

2 комментария для “VBA Excel. Число Пи (значение)”

Использование функции ПИ

Смотреть видеоФункция ПИ в Excel

Прикреплённые документы

Файлы для загрузки

Функция EXP в Excel

Вычисление экспоненты в Эксель

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Способ 2: использование Мастера функций

Способ 3: построение графика

Описание

Синтаксис

Замечания

Пример

Сводка сочетаний клавиш

Введите символ в Windows

Введите символ Pi с помощью сочетаний клавиш Alt-кода

Использование метода Alt + X в Word

Ввод символа Pi в приложениях Microsoft Office

Использование редактора формул

Введите символ Пи с картой символов

Использование панели эмодзи в Windows 10

Введите символ Pi в Mac

Использование ввода шестнадцатеричного кода

Использование программы просмотра персонажей

Введите символ в HTML и CSS

Варианты символов

Получение значения Пи

Смотреть видео
Функция ПИ в Excel